Desplazamiento caso base de una recurrencia
Caso base desplazado en una recurrencia
En el primer tema de esta serie presentamos las Funciones generadoras en una variable como introducción al uso de las funciones generadoras para resolver recurrencias. Repetimos unos ejemplos que ya se habían resuelto usando la técnica de la ecuación característica en el tema Recursivos que reducen mediante substracción.
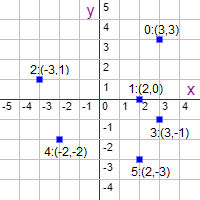
Un ejemplo de este tema que no usamos fue el de la recurrencia del algoritmo para obtener la menor distancia entre dos puntos (Figura). Todos estos ejemplos que en su día resolvimos usando la ecuación característica ahora los resolvemos usando la técnica de la función generadora. Pero con este de la menor distancia tenemos que ver antes que significa tener un caso base desplazado. Empecemos planteando el algoritmo.
Tenemos un Array con puntos del plano [p0, p1, ..., pn-1] siendo cada punto pi = [xi, yi] también un Array. El problema es buscar dos puntos cuya distancia entre ellos sea la menor entre todas las posibles. Por ejemplo, en la Figura vemos que esos dos puntos son el 1 y el 3.
El algoritmo era el siguiente:
function distancia(puntos=[], n=puntos.length){
numIter++;
if (n<2){
return [-1, -1, Infinity];
} else {
let [p, index, d] = [n-1, -1, Infinity];
let [x1, y1] = puntos[p];
for (let i=0; i<p; i++){
numIter++;
let [x2, y2] = puntos[i];
let dis = Math.sqrt((x1-x2)**2+(y1-y2)**2);
if (dis < d){
d = dis;
index = i;
}
}
let s = distancia(puntos, p);
if (s[2] < d){
return s;
} else {
return [p, index, d];
}
}
}La recurrencia planteada era así:
| T(n) = { | 1 | si n<2 |
| T(n-1) + n | si n≥2 |
Usando la técnica de la ecuación característica llegábamos a esta solución:
| T(n) = | n2+n |
| 2 |
Vea que el planteamiento, en cuanto a definir el caso base, equivale a lo siguiente:
| T(n) = { | 1 | si n≤1 |
| T(n-1) + n | si n>1 |
Entonces el caso base es n=1, pues viene a ser el valor de n necesario para que la recurrencia finalice. Es decir, si decimos que nb = 1 es el caso base, entonces con n≥nb la recurrencia finalizará cuando se alcance el caso base, es decir, cuando n = nb = 1. Es obvio que si empezamos con un n≥1 nunca alcanzaremos el caso n=0, por lo que quizás la definición quedaría mejor planteada así
| T(n) = { | 1 | si n=0 |
| 1 | si n=1 | |
| T(n-1) + n | si n>1 |
Tenemos que permitir una llamada con una longitud de n=0,en cuyo caso no se ejecuta la recurrencia pero si el algoritmo con un coste unitario. Por eso los casos inferiores al caso base forman parte del algoritmo y de su definición de la recurrencia, pero no de la propia recurrencia a la hora de resolverla.
La herramienta Wolfram Alpha puede resolver algunas recurrencias de forma directa. Si resolvemos la recurrencia T(n) = T(n-1) + n con distintos casos bases veremos lo que pasa:
| Caso base | Solución | 0 | 1 | 2 | 3 | 4 | 5 | 6 | Wolfram Alpha |
|---|---|---|---|---|---|---|---|---|---|
| T(0)=1 | T(n) = ½(n2+n+2) | 1 | 2 | 4 | 7 | 11 | 16 | 22 | WA |
| T(1)=1 | T(n) = ½(n2+n) | 1 | 3 | 6 | 10 | 15 | 21 | WA | |
| T(2)=1 | T(n) = ½(n2+n-4) | 1 | 4 | 8 | 13 | 19 | WA | ||
| T(3)=1 | T(n) = ½(n2+n-10) | 1 | 5 | 10 | 16 | WA | |||
| T(4)=1 | T(n) = ½(n2+n-18) | 1 | 6 | 12 | WA |
La segunda es la de nuestro problema con T(1) = 1, cuya solución ½(n2+n) es la misma que alcanzamos usando la técnica de la ecuación característica. Se observa que Wolfram Alpha no ofrece valor para n<1. Y con los siguientes para n < 2, 3, .... Podemos decir que la recurrencia no queda definida para valores inferiores al del caso base. Además se observa que se obtienen distintas secuencias, no sólo es un desplazamiento de los valores, sino que la solución obtenida es distinta según el caso base usado.
Podemos denominar a este efecto como desplazamiento del caso base, pues de alguna forma natural el caso base que se espera es T(0) = 1 y sin embargo nuestro algoritmo necesita desplazarlo hasta T(1) = 1. Y esto tiene un efecto cuando apliquemos la función generadora como veremos en los siguientes apartados.
No debe confundirse esto con las recurrencias que tiene más de un caso base debido a que hay más términos recurrentes, como con la del coste del algoritmo para calcular Fibonacci que ya vimos:
En este caso tenemos dos términos recurrentes T(n-1) y T(n-2) por lo que tendrán que haber al menos dos casos base, siendo cada caso base el menor posible que se alcanza cuando ejecutamos con n≥2. Por lo tanto aquí no hay desplazamiento de caso base, siendo el caso base mínimo n=0, viendo que partiendo de n≥2 siempre alcanzaremos esos dos casos base.
Sea con o sin desplazamiento, siempre tomaremos el caso base mínimo al que puede llegar la recurrencia partiendo de valores de n que no sean casos base. Ese mínimo es el que solemos usar como índice inicial del rango del sumatorio de la función generadora, como veremos a continuación.
Resolución con función generadora para un caso base desplazado
La definición de la recurrencia es la siguiente:
Ajustamos para evitar índices negativos:
Usamos la función generadora de serie de potencias:
Observe que ahora usamos n≥1 pues el caso base está desplazado en n=1 y, de alguna forma, ese es el rango o dominio de funcionamiento de la recurrencia.
La condición inicial para ese caso base es:
Volvemos a ver en lo resaltado en amarillo que la condición inicial es para n=1, no interviniendo n=0 y, por tanto, G0(x), en forma alguna.
Aplicamos la función generadora a la recurrencia [1], es decir, multiplicamos cada término por xn y sumamos:
Resolvemos cada término de [2]:
| = | 1 | ∑n≥1 T(n+1) xn+1 = | 1 | ∑n≥2 T(n) xn= |
| x | x |
| = | 1 | ( - T(1) x1+ ∑n≥1 T(n) xn ) | = |
| x |
| = | 1 | ( - G1(x) + G(x) ) | = |
| x |
| = | 1 | ( G(x) - x ) | = |
| x |
Observe que la única condición inicial que usamos es G1(x), no usándose G0(x). El siguiente término de [2] es la propia función generadora:
El siguiente en [2] es:
Aquí aplicaremos el siguiente principio de derivadas de una serie. Si A(x) es la función generadora de la serie ∑n≥0 an xn entonces si A'(x) es la derivada de aquella función tenemos que x A'(x) = ∑n≥1 n an xn.
Si identificamos an = 1 estamos con la serie geométrica con A(x) = 1 / (1-x), siendo su derivada A'(x) = 1 / (1-x)2, así que:
| ∑n≥1 n xn = ∑n≥1 n (1) xn = | x |
| (1-x)2 |
Y finalmente en [2] es obviamente la serie geométrica desplazada:
| ∑n≥1 xn = - x0 + ∑n≥0 xn = - 1 + | 1 |
| (1-x) |
Sustituimos [3], [4], [5] y [6] en [2]:
| 1 | ( G(x) - x ) = G(x) + | x | - 1 + | 1 |
| x | (1-x)2 | 1-x |
De donde obtenemos:
| G(x) = | x |
| (1-x)3 |
Para obtener las series simplificamos en fracciones simples:
| G(x) = | x | = | 1 | - | 1 | = f(x) - g(x) |
| (1-x)3 | (1-x)3 | (1-x)2 |
Resolvemos cada parte.
| f(x) = | 1 |
| (1-x)3 |
Si desarrollamos por Taylor, las primeras derivadas son las siguientes, donde intuimos un posible término general
Esto nos conduce a la siguiente serie:
| 1 | = ∑n≥0 | f n(0) | xn | = ∑n≥0 | (n+1)! ½ (n+2) | xn = |
| (1-x)3 | n! | n! |
| = ∑n≥0 | (n+2)! | xn | = | (0+2)! x0 | + ∑n≥1 | (n+2)! | xn | = |
| 2 | n! | 2·0! | 2 | n! |
| = 1 + ∑n≥1 | (n+2)(n+1) xn |
| 2 |
En los últimos pasos ajustamos el índice del sumatorio a n≥1 para hacerlo coincidir con la serie que deseamos obtener.
Veamos la segunda parte:
| g(x) = | 1 |
| (1-x)2 |
Si desarrollamos por Taylor, las primeras derivadas son:
Ya se observa una posible solución de tal forma que
| 1 | = ∑n≥0 | gn(0) | xn | = ∑n≥0 (n+1)! | xn | = |
| (1-x)2 | n! | n! |
| = | (0+1)! x0 | + ∑n≥1 (n+1)! | xn | = |
| 0! | n! |
También ajustamos a n≥1 para hacerlo coincidir con la serie que deseamos obtener. Finalmente la solución es
| G(x) = | x | = f(x) - g(x) = |
| (1-x)3 |
| = 1 + ∑n≥1 | (n+2)(n+1) xn | - 1 - ∑n≥1 (n+1) xn | = |
| 2 |
| = ∑n≥1 | (n2+n) | xn |
| 2 |
En Wolframalpha puede comprobarse ese resultado
| G(x) = | x | = ∑n≥1 | (n2+n) | xn |
| (1-x)3 | 2 |
Se observa que coincide con el rango n≥1, siendo el término general el mismo que vimos en el apartado anterior:
| T(n) = | n2+n |
| 2 |