Sudoku: Fish. X-Wing, Swordfish y Jellyfish
Fish
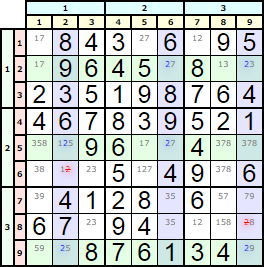
El grupo Fish de técnicas de resolución de un Sudoku se basa en una rejilla de n×n celdas que comprende 'n' conjuntos fila × 'n' conjuntos columna, o viceversa. En las intersecciones entre filas y columnas hemos de encontrar un disponible al menos en dos de ellas. Uno de los conjuntos se denomina conjunto base y el otro conjunto cobertura.
En la Figura puede ver un Swordfish con tres filas base con color verde de fondo y tres columnas cobertura, con color morado de fondo. En los conjuntos base el disponible '2' sólo aparece en las intersecciones, al menos en dos de ellas. En los conjuntos cobertura aparecen también al menos en dos celdas intersección y en cualquiera del resto de celdas, donde pueden ser eliminados.
El grupo Fish comprende las siguientes técnicas según su dimensión 'n×n':
| Dimensión | Técnica |
|---|---|
| 2×2 | X-Wing |
| 3×3 | Swordfish |
| 4×4 | Jellyfish |
| 5×5 | Squirmbag |
| 6×6 | Whale |
| 7×7 | Leviathan |
A partir del Jellyfish es muy díficil conseguir ejemplos, lo que evidencia que se dan en pocos casos. Y es posible que los Sudokus que los contengan también puedan resolverse con otras técnicas. En cualquier caso sólo contemplaré hasta el 4×4 Jellyfish. Las técnicas implementadas en la aplicación de gestión de Sudokus son las siguientes:
- Fish
- X-Wing en el grupo Fish
- Pez espada (Swordfish)
- Medusa (Jellyfish)
- Finned X-Wing
- Finned Swordfish
- Finned Jellyfish
- Sashimi X-Wing
- Sashimi Swordfish
- Sashimi Jellyfish
- Franken X-Wing
- Franken Swordfish
- Franken Jellyfish
- Finned Franken Swordfish (base)
- Finned Franken Swordfish (cover)
- Finned Franken Swordfish (2 boxs)
- Sashimi Franken Swordfish (base)
- Sashimi Franken Swordfish (cover)
Vemos que hay tres variantes básicas X-Wing, Swordfish y Jellyfish. Luego encontramos las variantes Finned, Sashimi y Franken. En este tema y siguientes expondré cada una de estas técnicas.
X-Wing en el grupo Fish
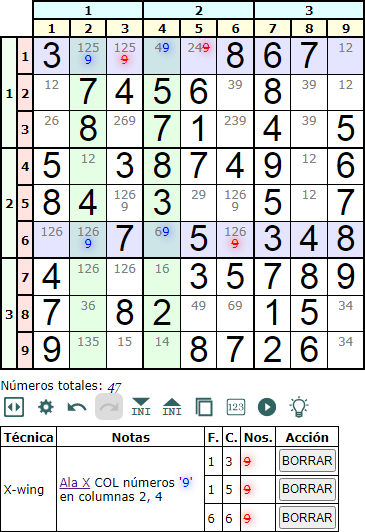
En un tema anterior X-Wing incluimos esa técnica dentro del grupo Wing, informando que lo hacíamos así teniendo en cuenta que desde el punto de vista estructural también podía incluirse en el grupo Fish. En la Figura puede ver un ejemplo de un X-Wing en columna. Repetiremos aquí el funcionamiento de esta técnica para que quede integrada también con el grupo Fish, al menos desde el punto de vista conceptual.
Esta técnica, que ya explicamos en el tema indicado, se basa en encontrar cuatro celdas que contengan un número disponible, como el '9' en el ejemplo. Como es en columna, hemos de fijarnos en las dos columnas con fondo verde, donde el '9' solo aparece en los disponibles de las cuatro celdas intersección. Estas interseccionan con las dos filas con fondo morado ubicadas en dos bandas distintas. En esas condiciones podemos eliminar la aparición del '9' en las celdas de las filas de color morado. Explicamos en aquel tema que el '9' tendría que ir obligatoriamente en esquinas opuestas en diagonal, lo que nos permite las eliminaciones propuestas.
Podemos razonar de otra forma la corrección de la técnica basándonos en que en cada fila habrán dos celdas intersección con un 'n', debiendo ir obligatoriamente en alguna de ellas pues la restricción de las columnas lo impone. Recuerde que antes dijimos que 'n'='9' aparece en las columnas verdes solo en las celdas intersección, por lo que deben ir ahí obligatoriamente. Así que desde el punto de vista de la fila es similar a tener un Naked pair, fijando 'n' en las celdas de la pareja y pudiendo eliminar 'n' del resto de celdas de la fila.
En cualquier caso y a efectos de la aplicación de gestión de Sudokus seguiré manteniendo X-Wing en el grupo Wing y no en el Fish. Sin embargo, sus variantes Finned, Sashimi y Franken estarán en Fish.
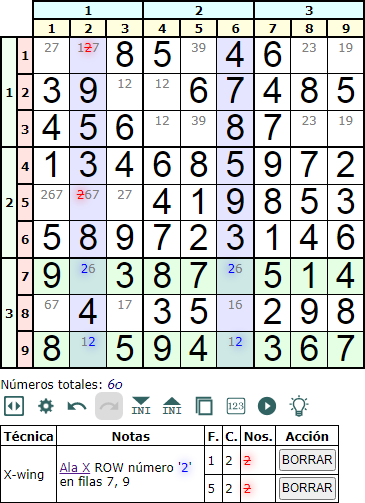
En la Figura se observa un X-Wing en fila que afecta al número 'n' = '2'. Las filas con fondo verde conforman la base mientras que las columnas con fondo morado son la cobertura (o cover en inglés). En los conjuntos base sólo encontraremos el disponible 'n' en las celdas intersección con las con los conjuntos cobertura (cover). El resto de apariciones de 'n' en la cobertura pueden entonces ser eliminados. Explicamos esto para el X-Wing porque aplicará también al resto de técnicas Fish.
Pez espada (Swordfish)
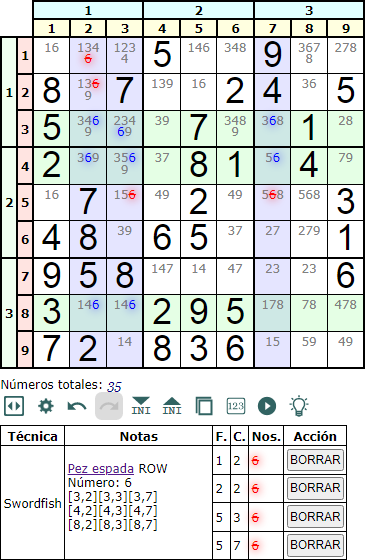
La técnica de resolución o profundizado de un Sudoku denominada Pez Espada en fila (Swordfish row) se basa en encontrar tres filas donde un número disponible 'n' se encuentre sólo en las celdas de esas filas que interseccionan con tres columnas. En la Figura puede ver un ejemplo. El '6' aparece en las filas con fondo verde (bases) solo en las intersecciones con las columnas de fondo morado (coberturas). Vemos que en las dos primeras filas hay tres celdas intersección que contienen el '6', mientras que en la última sólo hay dos. No es, por tanto, necesario que todas las celdas intersección contengan el número '6', algo que es muy díficil que suceda. Lo mínimo imprescindible es que cada fila y cada columna contenga al menos dos números. Este ejemplo lo hemos subtitulado 332 puesto que hay dos filas con tres números y una con dos.
Si eso sucede podemos eliminar todos los disponibles '6' de las celdas de las columnas, a excepción de las celdas intersección. Vemos en el ejemplo que se consigue eliminar números en las tres columnas.
El razonamiento es similar al que antes expusimos para el X-Wing. Se basa en que en cada columna habrán dos o tres celdas con un 'n', debiendo ir obligatoriamente en alguna de ellas pues la restricción de las filas lo impone. Así que desde el punto de vista de la columna es similar a tener un Naked pair o un Naked trio, fijando 'n' en las celdas de la pareja o trio y pudiendo eliminar 'n' del resto de celdas de la columna.
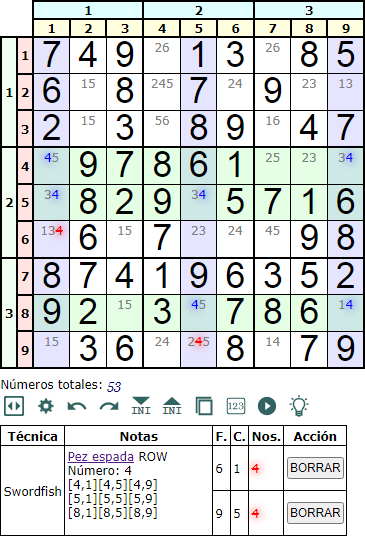
En la Figura vemos otro Swordfish Row 222, es decir, con dos celdas intersección con el número '4', algo que se cumple en las tres filas y las tres columnas. Cada fila y cada columna tendrá como mínimo dos celdas intersección con el número considerado, '4' en este ejemplo.
Otro detalle a tener en cuenta es que hay dos filas en la misma banda central. De hecho creo que no hay restricción alguna en cuanto a la ubicación de las filas en las bandas o de las columnas en las pilas.
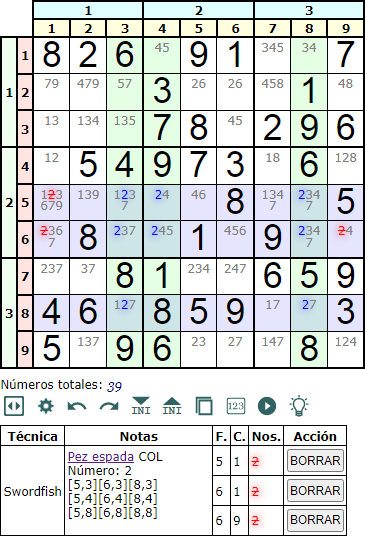
En la Figura vemos un ejemplo de un Pez espada en columna (Swordfish column). Hay tres columnas con fondo verde que interseccionan con tres filas con fondo morado. Vemos que el número '2' solo aparece en las celdas intersección de las columnas. Hay dos filas y dos columnas que tienen tres celdas intersección con el número '2'. Y una fila y una columna que tiene dos. Ese es el motivo de subtitular 332 a este ejemplo. Eliminamos el '2' de las filas con el mismo razonamiento que aplicamos en el apartado anterior.
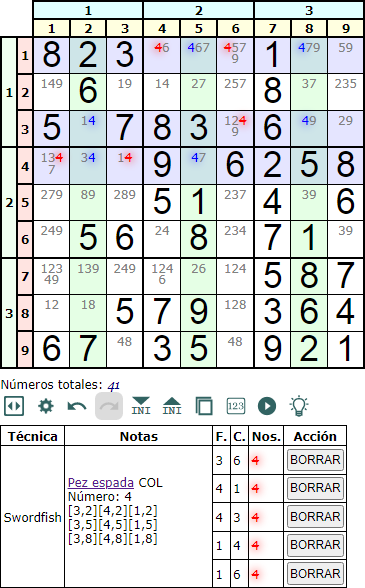
La Figura muestra un ejemplo de un Swordfish en columna con una estructura 222. Cada fila y columna tienen dos celdas intersección con el número disponible '4'. Podemos eliminar ese número del resto de celdas de las filas.
Medusa (Jellyfish)
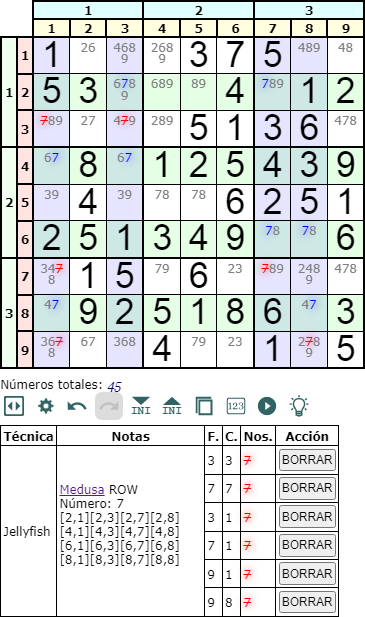
La técnica de resolución o profundizado de un Sudoku denominada Medusa en fila (Jellyfish row) se basa en encontrar cuatro filas donde un número disponible 'n' se encuentre sólo en las celdas de esas filas que interseccionan con cuatro columnas. En la Figura puede ver un ejemplo con 'n'='7'. Como con el Swordfish, no es necesario que todas las celdas intersección contengan 'n', pero el mínimo es que todas las filas y columnas contengan al menos dos celdas intersección con 'n'. Esto es lo que sucede con este ejemplo, donde las cuatro filas y columnas afectadas tienen dos celdas intersección con el '7' en sus disponibles.
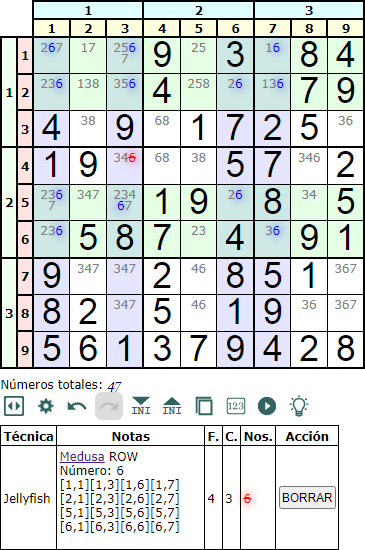
Esta técnica es muy poco frecuente y menos cuando hay más de dos celdas intersección por fila o columna. En este ejemplo de la Figura de otro Jellyfish en fila encontramos filas y columnas con 4, 3 y 2 celdas intersección que contienen el '6'. Sin embargo solo hay un número a eliminar.
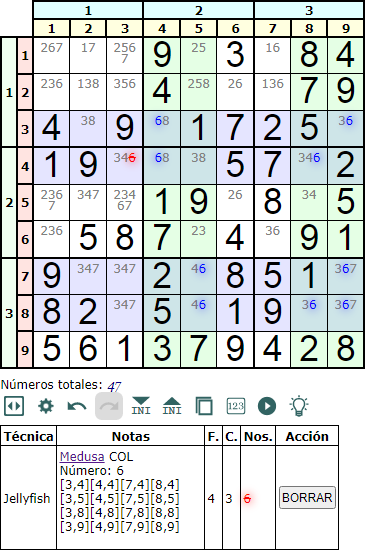
Parece ser que los Jellyfish en fila contienen otro complementario en columna. Y viceversa. Por ejemplo, la Figura presenta el mismo tablero que el del ejemplo anterior pero ahora en columna. Para obtenerlo he bloqueado la búsqueda de Jellyfish en fila y desbloqueado en columna para que puede detectar solo los de columna. Se observa que se obtiene la misma y única eliminación.
Hasta el momento todos los Jellyfish en fila que he generado tienen un complementario en columna con los mismos números a eliminar. Y de fuentes externas no he podido encontrar ningún ejemplo de lo contrario. Parece ser que esto aconseja buscar Jellyfish sólo en fila o en columna, pero no en ambos. Por ese motivo ofreceré la posibilidad de desactivar la búsqueda en columna (o en fila) en la aplicación de gestión de Sudokus.
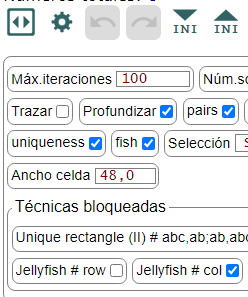
He incorporado en la aplicación de gestión de Sudokus unos controles para bloquear o desbloquear algunas técnicas. Son técnicas de las cuáles no he podido obtener ningun ejemplar. O bien otras situaciones, como esta que nos ocupa del Jellyfish. Se observa en la Figura un grupo de técnicas bloqueadas. La situación inicial es que el Jellyfish en fila está desbloqueado y en columna bloqueado. Si los marcamos al revés podemos comprobar como el ejemplo anterior en fila es encontrado su complementario en columna.