Finned X-Wing

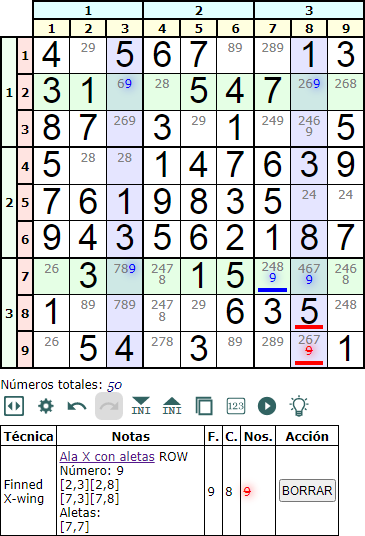
En la Figura puede ver un Ala X con aletas en fila (Finned X-Wing row). Sin considerar la celda [7,7], vemos que es un X-Wing con el número '9' que aparece en las cuatro intersecciones entre las filas base (color verde) y las columnas cobertura (color morado). Precisamente es esa celda [7,7] la aleta (fin) que encontramos en una fila base la que impide que sea un X-Wing verdadero. En la imagen la hemos resaltado con una línea inferior azul. Aún así nos permite eliminar los disponibles '7' en las celdas de la cobertura en la misma caja (señaladas con una línea roja inferior, apareciendo un '9' a eliminar en la celda [9,8].

Podemos decir que un Finned fish es un fish al que le sobran disponibles en celdas de un conjunto base. Estos que sobran los denominamos aletas. En este ejemplo está de más el '9' de la celda [7,7].

Se observa que el '9' aparece en otras celdas de las columnas cobertura que no son intersección, pero sólo podemos eliminar los '9' de la caja donde se ubica la aleta. El razonamiento es que el '9' debe ir en las intersecciones de forma alternativa. Si va en la [2,3] irá también en la [7,8] y si va en la [2, 8] irá también en [7,2]. Esto hace que el '9' irá necesariamente en alguna de las dos celdas de la caja con aleta, o va en [7,7] o en [7,8], por lo que podemos eliminar el '9' de la celda de cobertura [9,8].

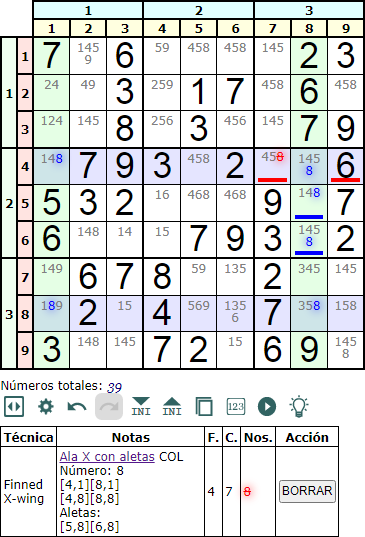
En la Figura vemos un Ala X con aletas en columna (Finned X-Wing column) con el número '8'. Las bases son las columnas con fondo verde y las coberturas son las filas con fondo morado. Este caso vemos que hay dos aletas en las celdas [5,8] y [6,8], eliminándose un '8' en la celda [4,7]. Comprobamos que en las bases el número '8' sólo aparece en las intersecciones con las coberturas y en las aletas.

Finned Swordfish

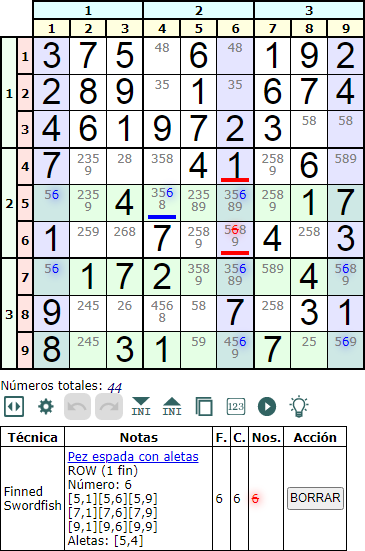
En la Figura vemos un Pez espada con aletas en fila (Finned Swordfish row) con el número '6'. Tenemos tres filas base con fondo verde y tres columnas cobertura con fondo morado. Para configurar un Swordfish el '6' debe aparecer al menos en dos de las tres intersecciones en cada fila base (color verde) o columna cobertura (color morado). Es la aparición de un '6' en la celda [5,4] lo que lo convierte además en un Finned Swordfish, eliminándose el disponible '6' de la celda [6,6].

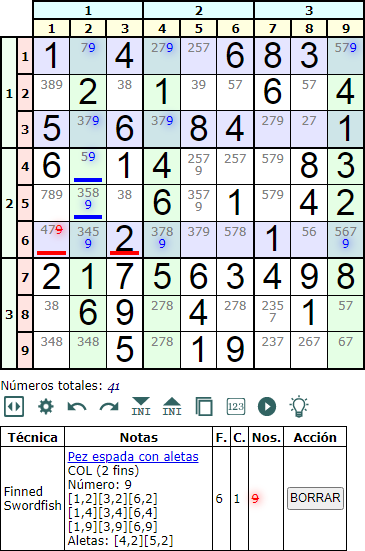
La Figura expone un Pez espada con aletas en columna (Finned Swordfish column) con el número '9'. En este caso tenemos una aleta doble en las celdas [4,2] y [5,2], eliminándose el '9' de la celda [6,1].

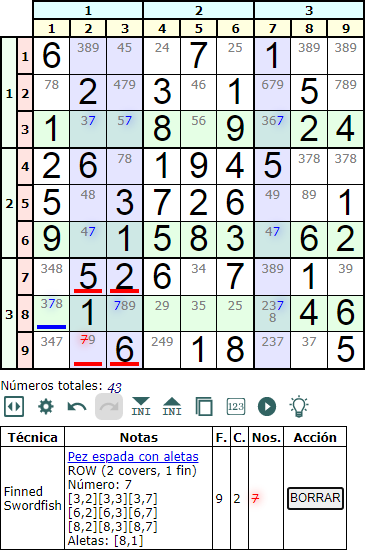
En la Figura vemos una Pez espada con aletas en fila (Finned Swordfish row) con el número '7', con dos columnas de cobertura en la misma pila (2 covers). Vemos la aleta en [8,1] y cuatro posibilidades de eliminación en las celdas cobertura que están en la caja de la aleta (celdas con línea roja), aunque en este caso sólo aparece un '7' a eliminar en la celda [9,2].

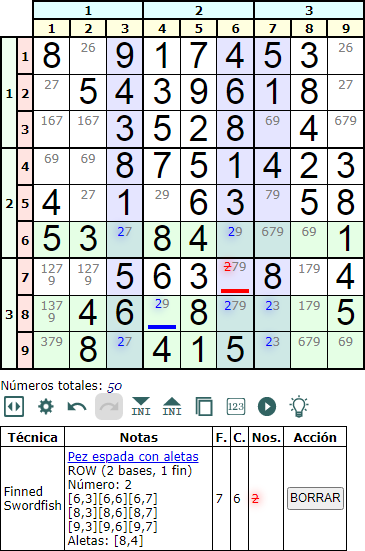
En la Figura vemos una Pez espada con aletas en fila (Finned Swordfish row) con el número '2' y con dos filas base en la misma banda (2 bases). En este caso sólo podemos eliminar un disponible en la celda [7,6].

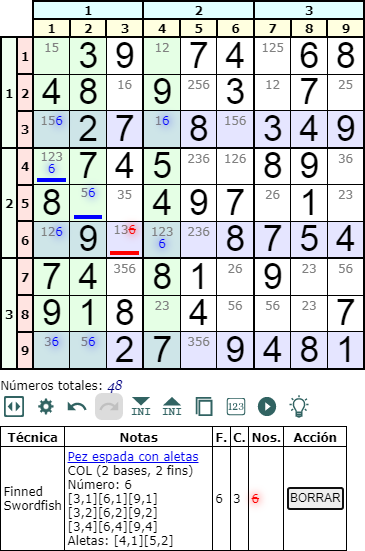
En la Figura vemos una Pez espada con aletas en columna (Finned Swordfish column) con el número '6' y con dos columnas base en la misma pila (2 bases). Ahora aparecen dos aletas en [4,1] y [5,2]. En cualquier caso sólo podemos eliminar un disponible en la celda [6,3].

Finned Jellyfish

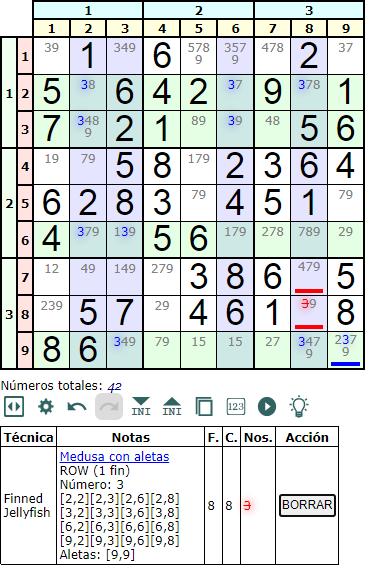
En la Figura vemos una Medusa con aletas en fila (Finned Jellyfish row) con el número '3'. Hay cuatro filas base (color verde) y cuatro columnas cobertura (color morado). La aleta en [9,9] impide que sea un verdadero Jellyfish, pero aún así nos permitirá eliminar el '3' de la celda [8,8].

En la Figura vemos una Medusa con aletas en columna (Finned Jellyfish column) con el número '5'. Hay cuatro columnas base (color verde) y cuatro filas cobertura (color morado). La aleta en [1,8] impide que sea un verdadero Jellyfish, pero aún así nos permite eliminar el '5' de la celda [3,9].

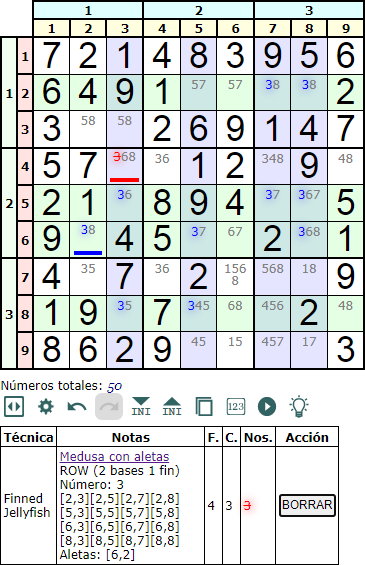
En la Figura vemos una Medusa con aletas en fila (Finned Jellyfish row) con el número '3'. Dos filas base (color verde) aparecen en la misma banda de la caja donde vemos la aleta en [6,2]. En este caso sólo tenemos una posibilidad de eliminación en la celda [4,3].

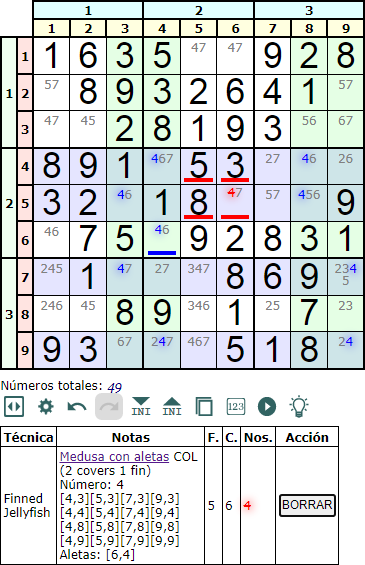
En la Figura vemos una Medusa con aletas en columna (Finned Jellyfish column) con el número '4'. Aparecen dos filas cobertura (2 covers) en la misma banda donde se ubica la aleta [6,4]. En este caso podemos tener hasta cuatro posibles celdas para eliminar (celdas con línea roja), aunque en este ejemplo sólo hay un '4' a eliminar en la [2,6].

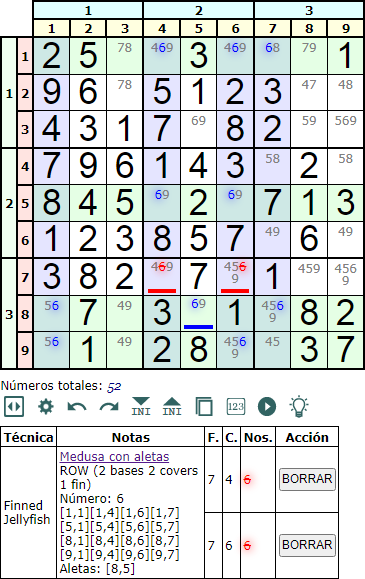
En la Figura vemos una Medusa con aletas en fila (Finned Jellyfish row) con el número '6'. En este caso tenemos dos filas base y dos columnas cobertura (2 bases 2 covers) coincidiendo en la caja donde se ubica la aleta [8,2], donde se pueden eliminar dos números, como en el ejemplo que eliminamos el '6' en las celdas [7,4]y [7,6].