Encontrar máximo flujo en un grafo
Encontrar máximo flujo en un grafo findMaximumFlow()
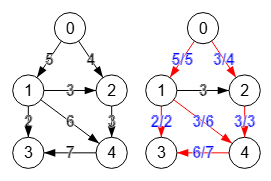
Una red de flujo puede representarse en un grafo dirigido ponderado donde los pesos representan las capacidades de las aristas, con un nodo identificado como fuente (source) tomando sólo las aristas salientes y otro identificado como sumidero (sink) tomando sólo las aristas entrantes, considerando que la dirección de la aristas representan un flujo existente desde la fuente hasta el sumidero. El flujo puede ser cualquier cosa que fluye en una unidad de tiempo, como litros de agua que pasan por una tubería, número de vehículos que pasan por una carretera, etc.
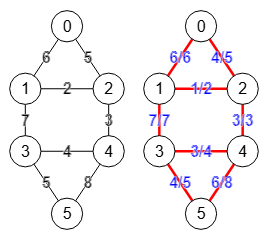
En el grafo de la izquierda de la Figura consideramos el nodo "0" como fuente y el "3" como sumidero, observando que hay flujo entre esos dos nodos. La arista "0🡒1" tiene capacidad "5" significando que por esa arista no puede fluir más de 5 unidades. Por la arista "0🡒4" no puede fluir más de 4 unidades. Obviamente el flujo máximo parece ser 5+4 = 9, pues además las aristas finales "1🡒3" y "4🡒3" permiten precisamente esa capacidad 2+7 = 9 (aunque no es necesario que coincidan), pero el resto de capacidades también intervienen, con lo que ese valor puede verse reducido, como efectivamente veremos que será 8.
El algoritmo encontrar máximo flujo del grafo se refiere entonces a calcular cuál es la cantidad máxima de flujo que puede circular desde el nodo fuente hasta el nodo sumidero sin superar las capacidades de las aristas. En el grafo resultado de la derecha de la Figura vemos las capacidades usadas en cada arista. Así en "0🡒1" se usan todas las capacidades "5/5" que significa "5 de 5". En "0🡒4" se usan "3/4". En las aristas entrantes que llegan al nodo sumidero "1🡒3" y "4🡒3" se usan "2/2" y "6/7" respectivamente, siendo precisamente la suma 2 + 6 = 8 el valor final del flujo máximo que puede circular por esa red, valor que es igual que las capacidades usadas en las aristas salientes del nodo fuente 5 + 3 = 8.
Vea que la suma de las capacidades usadas o flujo en las aristas entrantes a un nodo es igual que la suma de las aristas salientes. Por ejemplo, al nodo "1" entra "5/5" y salen "2/2" y "3/6" así que 5 = 2+3.
Algunas aristas no intervienen en el flujo como la "1🡒2". Además se observa que es la arista "2🡒4" con capacidad "3" la que limita el flujo máximo con valor "4" que pudiera llegarle desde la arista "0🡒2". Si esa arista "2🡒4" tuviera capacidad "4" entonces el flujo máximo sería 9.
0 5 4 0 0 0 0 3 2 6 0 0 0 0 3 0 0 0 0 0 0 0 0 7 0
Esta es la matriz de adyacencia ponderada del grafo inicial.
Encontrar máximo flujo: {
"flow":8,
"residualMatrix":
[[0,0,1,0,0],
[5,0,3,0,3],
[3,0,0,0,0],
[0,2,0,0,6],
[0,3,3,1,0]],
"flowMatrix":
[[0,5,3,0,0],
[0,0,0,2,3],
[0,0,0,0,3],
[0,0,0,0,0],
[0,0,0,6,0]],
"edgesFlow":
{"0,1":5,"0,2":3,"1,3":2,
"1,4":3,"2,4":3,"4,3":6}}Y este es el resultado obtenido donde vemos el máximo flujo en "flow":8 encontrado que es 8. La matriz residual en residualMatrix nos da las capacidades sin usar en cada arista. La matriz del flujo viene en flowMatrix así como la lista de aristas del flujo se nos da en edgesFlow, representando ambos el grafo y las aristas que intervienen en el máximo flujo. Luego explicaremos estas dos matrices, pero antes exponemos el JSON por si quiere importar el ejemplo en la aplicación:
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0,"value":5}]},
{"index":2,"parent":[{"index":0,"value":4},{"index":1,"value":3}]},
{"index":3,"parent":[{"index":1,"value":2},{"index":4,"value":7}]},
{"index":4,"parent":[{"index":1,"value":6},{"index":2,"value":3}]}
],
"config":{
"markerStart":"arrow",
"algorithm":"Find maximum flow",
"lastIndex":3
}}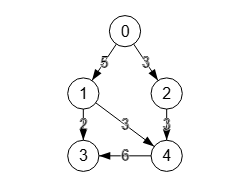
Veamos primero la matriz flowMatrix que se corresponde con el grafo del flujo que vemos en la Figura.
[[0,5,3,0,0], [0,0,0,2,3], [0,0,0,0,3], [0,0,0,0,0], [0,0,0,6,0]]
Esta es la matriz del flujo de ese grafo. Se observan las aristas que intervienen en el flujo máximo, con las capacidades que se usan en cada arista. Así en la arista "0🡒1" se usan todas las 5/5 capacidades. En la arista "0🡒3" se usan 3/4 y así sucesivamente. Vea que la arista "1🡒2" no se usa.
La lista de aristas que intervienen en el flujo son {"0,1":5, "0,2":3, "1,3":2, "1,4":3, "2,4":3, "4,3":6} que viene en el resultado edgesFlow, que es otra forma de presentar el grafo de flujo máximo. Observamos, por ejemplo, que la arista "0🡒1" usa 5 capacidades.
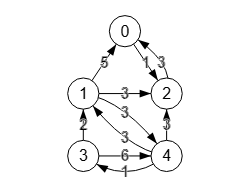
En la Figura vemos el grafo residual que representa las capacidades usadas y sin usar en cada arista. Por ejemplo, con la arista inicial "0🡒2" con capacidad 4 y que usa 3/4, vemos la arista "2🡒0" con las 3 capacidades usadas y la arista "0🡒2" con 1 capacidad restante sin usar. Todas las aristas que tengan la misma dirección que las iniciales presentan las capacidades sin usar, que son "0🡒2" (1), "1🡒2" (3), "1🡒4" (3) y "4🡒3" (1). Las aristas en dirección contraria a la inicial representan las capacidades usadas.
[[0,0,1,0,0], [5,0,3,0,3], [3,0,0,0,0], [0,2,0,0,6], [0,3,3,1,0]]
Esta es la matriz residual que puede importar con el siguiente JSON pues hemos separado visualmente las aristas dobles.
{"nodes":[
{"index":0,"nodeOffset":"16.67","parent":[{"index":-1},{"index":2,"value":1}]},
{"index":1,"parent":[{"index":0,"value":5},{"index":2,"value":3},{"index":4,"value":3,"lineType":"quadratic","lineOffset":"0 -1.6"}]},
{"index":2,"parent":[{"index":0,"value":3,"lineOffset":"2","lineType":"quadratic"}]},
{"index":3,"nodeOffset":"-16.67","parent":[{"index":1,"value":2},{"index":4,"value":6}]},
{"index":4,"nodeOffset":"0 50","parent":[{"index":1,"value":3,"lineOffset":"0 1.6","lineType":"quadratic"},{"index":2,"value":3},{"index":3,"value":1,"lineOffset":"0 2","lineType":"quadratic"}]}
],
"config":{
"markerEnd":"arrow"
}}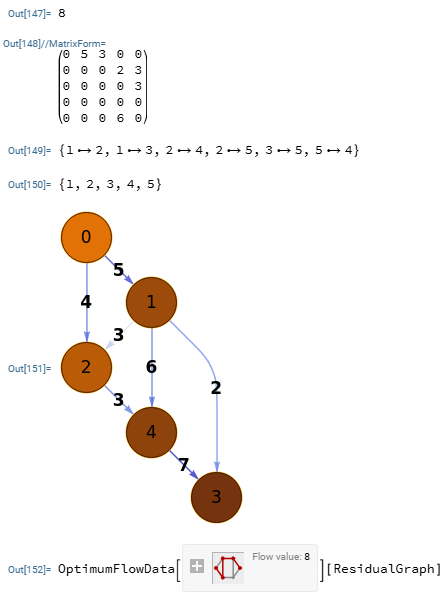
En la Figura vemos la exportación a Wolfram con la función FindMaximumFlow[g, s, t, "OptimumFlowData", EdgeCapacity->EdgeWeight]. Con "OptimumFlowData" nos devuelve un objeto con el valor del máximo flujo "FlowValue", la matriz del flujo "flowMatrix", la lista de aristas y vértices que intervienen en el flujo "EdgeList" y "VertexList", el grafo del flujo "FlowGraph" y el grafo residual "ResidualGraph".
Observamos que todos los resultados menos el grafo residual son iguales considerando que en Wolfram los índices se inician en "1" y en nuestra aplicación en "0". El grafo residual no es devuelto por Wolfram, pareciendo que hay un error en esa parte aunque no lanza ningún mensaje de error.
g = WeightedAdjacencyGraph[{{∞,5,4,∞,∞},{∞,∞,3,2,6},{∞,∞,∞,∞,3},{∞,∞,∞,∞,∞},{∞,∞,∞,7,∞}}, ImageSize->188,
VertexSize->{"Scaled", 0.17}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center]},
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(1->2)->5, (1->3)->4, (2->3)->3, (2->4)->2, (5->4)->7, (2->5)->6, (3->5)->3}, VertexStyle->White, DirectedEdges->True,
EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindMaximumFlow[g, 1, 4, "OptimumFlowData", EdgeCapacity->EdgeWeight];
f["FlowValue"]
MatrixForm[f["FlowMatrix"]]
f["EdgeList"]
f["VertexList"]
f["FlowGraph"]
f["ResidualGraph"]
En la Figura vemos las opciones de la aplicación para encontrar el máximo flujo: primer índice nodo y último índice de nodo para los nodos fuente y sumidero. Las opciones color camino y color texto no intervienen en el algoritmo y sólo aplican colores tras obtener el resultado y presentarlo en el grafo de la aplicación. Explicaremos la opción omitir pesos en el apartado siguiente para encontrar caminos con aristas independientes usando máximo flujo, pues ahora vamos a ver la opción método para flujo con los valores findPath, dijkstra y floyd.
El algoritmo para encontrar el máximo flujo va buscando caminos entre la fuente y el sumidero, para lo cual usa el algoritmo para encontrar camino (findPath()), que a su vez se basa en la búsqueda en profundidad recursiva (getDepthFirstSearchRecursive()).
Además del enfoque de búsqueda en profundidad, podemos usar cualquier método que descubra caminos entre el sumidero y la fuente. Como los algoritmos para encontrar el camino mínimo de Dijkstra y el camino mínimo de Floyd. Con cualquier método para descubrir caminos debe encontrarse el mismo valor del máximo flujo, aunque el grafo residual o el grafo de flujo o, equivalentemente, las aristas que intervienen en el flujo, no tiene que ser las mismas.
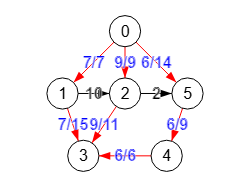
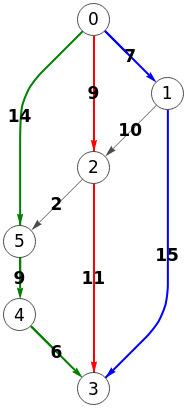
En la Figura vemos el máximo flujo entre nodos "0" y "3" usando el algoritmo findPath() con la matriz de adyacencia ponderada inicial siguiente:
0 7 9 0 0 14 0 0 10 15 0 0 0 0 0 11 0 2 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 9 0
Encontrar máximo flujo: {
"flow":22,
"residualMatrix":
[[0,0,0,0,0,8],
[7,0,10,8,0,0],
[9,0,0,2,0,2],
[0,7,9,0,6,0],
[0,0,0,0,0,6],
[6,0,0,0,3,0]],
"flowMatrix":
[[0,7,9,0,0,6],
[0,0,0,7,0,0],
[0,0,0,9,0,0],
[0,0,0,0,0,0],
[0,0,0,6,0,0],
[0,0,0,0,6,0]],
"edgesFlow":
{"0,1":7,"0,2":9,"0,5":6,
"1,3":7,"2,3":9,"4,3":6,"5,4":6}Este es el resultado obtenido, con un valor de flujo 22.
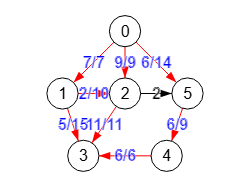
Usando el algoritmo de Dijkstra para descubrir camino mínimos encontramos el mismo valor máximo de flujo 22, aunque el grafo residual y el grafo de flujo no sean los mismos.
Encontrar máximo flujo: {
"flow":22,
"residualMatrix":
[[0,0,0,0,0,8],
[7,0,8,10,0,0],
[9,2,0,0,0,2],
[0,5,11,0,6,0],
[0,0,0,0,0,6],
[6,0,0,0,3,0]],
"flowMatrix":
[[0,7,9,0,0,6],
[0,0,2,5,0,0],
[0,0,0,11,0,0],
[0,0,0,0,0,0],
[0,0,0,6,0,0],
[0,0,0,0,6,0]],
"edgesFlow":
{"0,1":7,"0,2":9,"0,5":6,"1,2":2,
"1,3":5,"2,3":11,"4,3":6,"5,4":6}}Con Dijkstra obtenemos el mismo valor de flujo máximo 22, pero usa otros caminos para ir desde la fuente al sumidero. En azul resaltamos las diferencias con respecto al uso de findPath.
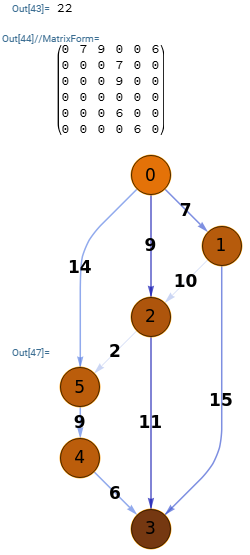
En la Figura vemos la exportación a Wolfram, obteniéndose el mismo valor 22 para el máximo flujo y la misma matriz de flujo que en nuestra aplicación usando findPath, de lo que deducimos que Wolfram usa un enfoque basado en búsqueda en profundidad para descubrir los caminos entre la fuente y el sumidero.
g = WeightedAdjacencyGraph[{{∞,7,9,∞,∞,14},{∞,∞,10,15,∞,∞},{∞,∞,∞,11,∞,2},{∞,∞,∞,∞,∞,∞},{∞,∞,∞,6,∞,∞},{∞,∞,∞,∞,9,∞}},
ImageSize->188, VertexSize->{"Scaled", 0.17}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center], 4->Placed[3,Center],
5->Placed[4,Center], 6->Placed[5,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(1->2)->7, (1->3)->9, (2->3)->10, (2->4)->15, (3->4)->11, (5->4)->6, (6->5)->9, (1->6)->14, (3->6)->2}, VertexStyle->White, DirectedEdges->True,
EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindMaximumFlow[g, 1, 4, "OptimumFlowData", EdgeCapacity->EdgeWeight];
f["FlowValue"]
MatrixForm[f["FlowMatrix"]]
f["EdgeList"]
f["VertexList"]
f["FlowGraph"]
f["ResidualGraph"]Encontrar máximo flujo en grafos no dirigidos
Definimos al inicio que una red de flujo se puede representar como un grafo ponderado y dirigido, donde los pesos representan las capacidades de las aristas, grafo sobre el cual tiene sentido encontrar el máximo flujo. Pero el algoritmo también funciona con un grafo no dirigido como el de la parte izquierda de la Figura, a pesar de que en un grafo no dirigido no puede entenderse el concepto de flujo.
0 6 5 0 0 0 6 0 2 7 0 0 5 2 0 0 3 0 0 7 0 0 4 5 0 0 3 4 0 8 0 0 0 5 8 0
Esta es la matriz de adyacencia de ese grafo, recordando que cuando las matrices son simétricas respecto a la diagonal derecha entonces se considera que el grafo es no dirigido. El mismo algoritmo para encontrar el máximo flujo funciona con esta matriz de adyacencia dado que considera que cada arista tiene la misma capacidad en una dirección y en la contraria, mostrándose el grafo de flujo correspondiente al máximo flujo entre los nodos "0" y "5" en la parte derecha de la Figura.
Encontrar máximo flujo: {
"flow":10,
"residualMatrix":
[[0,0,1,0,0,0],
[12,0,3,0,0,0],
[9,1,0,0,0,0],
[0,14,0,0,1,1],
[0,0,6,7,0,2],
[0,0,0,9,14,0]],
"flowMatrix":
[[0,6,4,0,0,0],
[0,0,0,7,0,0],
[0,1,0,0,3,0],
[0,0,0,0,3,4],
[0,0,0,0,0,6],
[0,0,0,0,0,0]],
"edgesFlow":
{"0,1":6,"0,2":4,"1,3":7,"2,1":1,
"2,4":3,"3,4":3,"3,5":4,"4,5":6}}Este es el resultado obtenido para encontrar el máximo flujo con valor 10 entre los nodos "0" y "5".
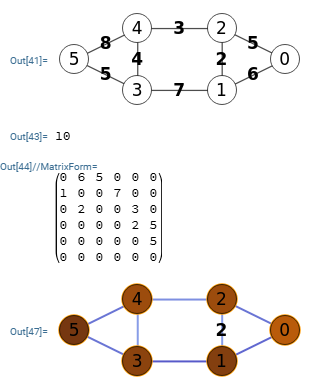
En la Figura vemos la exportación a Wolfram, con el grafo no dirigido inicial y el grafo de flujo. Se observa que no etiqueta las aristas (solo una de ellas) sin saber si se trata de un error.
Se obtiene el mismo valor 10 de máximo flujo, aunque la matriz de flujo no es igual, pero ya hemos dicho en el apartado anterior que pueden haber varias alternativas para encontrar caminos entre la fuente y el sumidero.
g = WeightedAdjacencyGraph[{{∞,6,5,∞,∞,∞},{6,∞,2,7,∞,∞},{5,2,∞,∞,3,∞},{∞,7,∞,∞,4,5},{∞,∞,3,4,∞,8},{∞,∞,∞,5,8,∞}},
ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center], 4->Placed[3,Center],
5->Placed[4,Center], 6->Placed[5,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(2->1)->6, (3->1)->5, (3->2)->2, (4->2)->7, (5->3)->3, (5->4)->4, (6->4)->5, (6->5)->8}, VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindMaximumFlow[g, 1, 6, "OptimumFlowData", EdgeCapacity->EdgeWeight];
f["FlowValue"]
MatrixForm[f["FlowMatrix"]]
f["EdgeList"]
f["VertexList"]
f["FlowGraph"]
f["ResidualGraph"]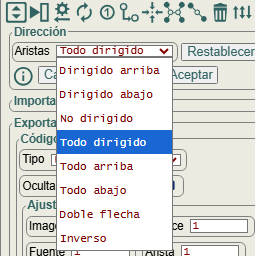
Veamos cuál es el motivo de que el algoritmo para encontrar el máximo flujo con grafos no dirigidos funcione. En primer lugar vamos a convertir el grafo no dirigido de la Figura en uno todo dirigido, usando la operación del JSON cambiar dirección del grafo como vemos en la Figura, abriendo el panel correspondiente con el botón

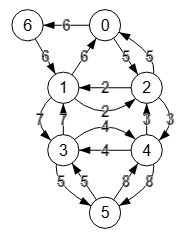
Al cambiar a todo dirigido obtenemos el grafo de la parte izquierda de la Figura, donde todas son dobles aristas, es decir, entre dos nodos "a" y "b" hay una arista "a🡒b" y otra "b🡒a", ambas con el mismo peso. Esto lo podemos ver mejor en el grafo de la derecha, donde hemos separado cada una de las dos aristas dobles con la propiedad lineOffset.
0 6 5 0 0 0 6 0 2 7 0 0 5 2 0 0 3 0 0 7 0 0 4 5 0 0 3 4 0 8 0 0 0 5 8 0
La matriz de adyacencia de este grafo todo dirigido sigue siendo la misma matriz simétrica que la del no dirigido. Es por ello que la matriz de adyacencia no puede representar un grafo todo dirigido, pues al ser simétrica se considera no dirigido. Esto lo explicamos en temas anteriores, en limitaciones de la matriz de adyacencia y en las aristas dobles.
Con este JSON puede importar el grafo todo dirigido de la derecha de la Figura.
{"nodes":[
{"index":0,"nodeOffset":"30","parent":[{"index":-1},{"index":2,"value":5},{"index":1,"lineType":"quadratic","lineOffset":"-3 -1","value":6}]},
{"index":1,"parent":[{"index":0,"value":6},{"index":2,"value":2,"lineType":"quadratic","lineOffset":"0 3"},{"index":3,"value":7,"lineType":"quadratic","lineOffset":"-3"}]},
{"index":2,"parent":[{"index":0,"value":5,"lineType":"quadratic","lineOffset":"3"},{"index":1,"value":2},{"index":4,"value":3,"lineType":"quadratic","lineOffset":"3"}]},
{"index":3,"nodeOffset":"-6.67 50","parent":[{"index":1,"value":7},{"index":4,"value":4,"lineType":"quadratic","lineOffset":"0 -3"},{"index":5,"value":5,"lineType":"quadratic","lineOffset":"-3"}]},
{"index":4,"nodeOffset":"6.67 50","parent":[{"index":2,"value":3},{"index":3,"value":4},{"index":5,"value":8,"lineType":"quadratic","lineOffset":"3"}]},
{"index":5,"nodeOffset":"-30 75","parent":[{"index":3,"value":5},{"index":4,"value":8}]}
],
"config":{
"markerEnd":"arrow"
}}Como todos los algoritmos de la aplicación se ejecutan sobre la matriz de adyacencia, no deberíamos usar esa matriz para encontrar el máximo flujo pues no representa un grafo dirigido y, por tanto, tampoco representará una red de flujo tal como la definimos al inicio de este tema.
Para solucionarlo podemos usar la operación subdivisión de una arista en el JSON, abriendo el panel correspondiente con el icono , subdividiendo la arista "0🡒1" con capacidad "6" en dos aristas "0🡒6" y "6🡒1" ambas también con la misma capacidad "6".
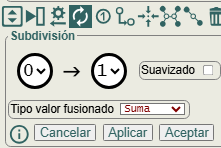
Es obvio que esto no limita la capacidad total del camino "0🡒6🡒1" que sigue siendo "6", con lo que el máximo flujo sería el mismo sin o con esa subdivisión.
0 0 5 0 0 0 6 6 0 2 7 0 0 0 5 2 0 0 3 0 0 0 7 0 0 4 5 0 0 0 3 4 0 8 0 0 0 0 5 8 0 0 0 6 0 0 0 0 0
Lo importante es que al insertar el nuevo nodo "6" ya la matriz no es simétrica, representando por tanto un verdadero grafo dirigido, con lo que es una red de flujo y por tanto se puede encontrar el máximo flujo. Observe en color azul que se elimina el "6" que había en la posición segunda de la primera fila y se crea una nueva columna y una nueva fila con ese valor en la intersección de ambas. Con el siguiente JSON puede importar ese grafo con la subdivisión.
{"nodes":[
{"index":0,"nodeOffset":"30","parent":[{"index":-1},{"index":2,"value":5},{"index":6,"value":6}]},
{"index":1,"parent":[{"index":0,"value":6},{"index":2,"value":2,"lineType":"quadratic","lineOffset":"0 3"},{"index":3,"value":7,"lineType":"quadratic","lineOffset":"-3"}]},
{"index":2,"parent":[{"index":0,"value":5,"lineType":"quadratic","lineOffset":"3"},{"index":1,"value":2},{"index":4,"value":3,"lineType":"quadratic","lineOffset":"3"}]},
{"index":3,"nodeOffset":"-6.67 50","parent":[{"index":1,"value":7},{"index":4,"value":4,"lineType":"quadratic","lineOffset":"0 -3"},{"index":5,"value":5,"lineType":"quadratic","lineOffset":"-3"}]},
{"index":4,"nodeOffset":"6.67 50","parent":[{"index":2,"value":3},{"index":3,"value":4},{"index":5,"value":8,"lineType":"quadratic","lineOffset":"3"}]},
{"index":5,"nodeOffset":"-30 75","parent":[{"index":3,"value":5},{"index":4,"value":8}]},
{"index":6,"nodeOffset":"-31 -50","parent":[{"index":1,"value":6}]}
],
"config":{
"markerEnd":"arrow"
}}
En la Figura vemos el grafo de flujo al encontrar el máximo flujo entre los nodos "0" y "5" para el grafo dirigido anterior con la subdivisión "0🡒1".
Encontrar máximo flujo: {
"flow":10,
"residualMatrix":
[[0,0,0,0,0,0,1],
[6,0,4,0,0,0,5],
[10,0,0,0,0,0,0],
[0,14,0,0,0,2,0],
[0,0,6,8,0,1,0],
[0,0,0,8,15,0,0],
[5,1,0,0,0,0,0]],
"flowMatrix":
[[0,0,5,0,0,0,5],
[0,0,0,7,0,0,0],
[0,2,0,0,3,0,0],
[0,0,0,0,4,3,0],
[0,0,0,0,0,7,0],
[0,0,0,0,0,0,0],
[0,5,0,0,0,0,0]],
"edgesFlow":
{"0,2":5,"0,6":5,"1,3":7,
"2,1":2,"2,4":3,"3,4":4,
"3,5":3,"4,5":7,"6,1":5}}El valor del máximo flujo es 10, igual que encontramos directamente con el grafo no dirigido que vimos al principio del apartado. Vea que la matriz de flujo no es igual que la obtenida con el grafo no dirigido, pero ya hemos dicho que esto no es relevante, pues dependiendo del grafo pueden haber múltiples caminos que llevan de la fuente al sumidero.
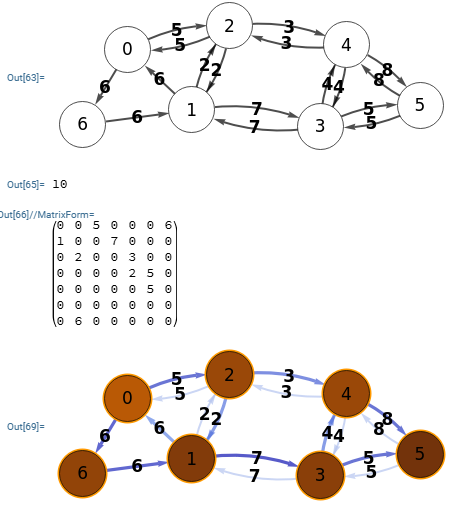
En la Figura vemos la exportación a Wolfram con el mismo máximo flujo con valor 10, aunque con otra matriz de flujo.
g = WeightedAdjacencyGraph[{{∞,∞,5,∞,∞,∞,6},{6,∞,2,7,∞,∞,∞},{5,2,∞,∞,3,∞,∞},{∞,7,∞,∞,4,5,∞},{∞,∞,3,4,∞,8,∞},{∞,∞,∞,5,8,∞,∞},{∞,6,∞,∞,∞,∞,∞}},
ImageSize->400, VertexSize->{"Scaled", 0.13}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center], 4->Placed[3,Center],
5->Placed[4,Center], 6->Placed[5,Center], 7->Placed[6,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(1->3)->5, (1->7)->6, (2->1)->6, (2->3)->2, (2->4)->7, (3->1)->5, (3->2)->2, (3->5)->3, (4->2)->7, (4->5)->4, (4->6)->5, (5->3)->3, (5->4)->4,
(5->6)->8, (6->4)->5, (6->5)->8, (7->2)->6}, VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindMaximumFlow[g, 1, 6, "OptimumFlowData", EdgeCapacity->EdgeWeight];
f["FlowValue"]
MatrixForm[f["FlowMatrix"]]
f["EdgeList"];
f["VertexList"];
f["FlowGraph"]
f["ResidualGraph"];Código JavaScript máximo flujo findMaximumFlow()
Exponemos a continuación el código JavaScript para ejecutar findMaximumFlow() usando las funciones siguientes:
getMatrixModeValue()para obtener el modo valor de la matriz.findPath()para encontrar un camino entre dos nodos con un enfoque de búsqueda en profundidad.getShortestPathDijkstrapara encontrar el camino mínimo entre dos nodos con el algoritmo de Dijkstra que publiqué hace años (en 2020) y que he implementado también en la aplicación.getShortestPathFloydpara encontrar el camino mínimo entre dos nodos con el algoritmo de Floyd que publiqué hace años (en 2020) y que he implementado también en la aplicación.
function findMaximumFlow({matrix=[], firstIndex=0, lastIndex=0, methodFlow="findPath", omitWeights=false}) {
let result = {flow: 0, residualMatrix: [], flowMatrix: [], edgesFlow: []}, temp;
try {
// copy matrix to not modify the original
let matrixCopy = [];
if (omitWeights){
if (temp = getMatrixModeValue({matrix}), typeof temp==="string") throw new Error(temp);
let [modeValue, nullValue] = temp;
for (let i=0; i<matrix.length; i++) {
let arr = []
for (let j=0; j<matrix.length; j++) {
let value = matrix[i][j]===nullValue ? 0 : 1;
arr.push(value);
}
matrixCopy.push(arr);
}
} else {
matrixCopy = matrix;
}
let residualMatrix = JSON.parse(JSON.stringify(matrixCopy));
let n = matrix.length;
let flowMatrix = Array.from({length: n}, () => Array.from({length:n}, () => 0));
let flow = 0;
let path = [null];
while (path.length>0) {
if (iter++, iter>maxIter) throw new Error(`Maximum iterations ${maxIter} reached`);
path = [];
if (methodFlow==="findPath") {
let tempPaths = findPath({matrix:residualMatrix, firstIndex, lastIndex});
if (typeof tempPaths==="string") throw new Error(tempPaths);
if (tempPaths.warning) throw new Error(tempPaths.warning);
if (tempPaths.length>0) path = tempPaths[0];
} else if (methodFlow==="dijkstra") {
let tempPath = getShortestPathDijkstra({matrix:residualMatrix, firstIndex, lastIndex});
if (typeof tempPath==="string") throw new Error(tempPath);
path = tempPath.path;
} else if (methodFlow==="floyd") {
let tempPath = getShortestPathFloyd({matrix:residualMatrix, firstIndex, lastIndex});
if (typeof tempPath==="string") throw new Error(tempPath);
path = tempPath.path;
} else {
throw new Error(`Method for flow wrong`);
}
if (path.length>0) {
let maxFlowPath = Infinity;
for (let i=1; i<path.length; i++) {
let [u, v] = [path[i-1], path[i]];
maxFlowPath = Math.min(maxFlowPath, residualMatrix[u][v]);
}
for (let i=1; i<path.length; i++) {
let [u, v] = [path[i-1], path[i]];
flowMatrix[u][v] += maxFlowPath;
flowMatrix[v][u] -= maxFlowPath;
residualMatrix[u][v] -= maxFlowPath;
residualMatrix[v][u] += maxFlowPath;
}
flow += maxFlowPath;
}
}
result.flow = flow;
result.residualMatrix = residualMatrix;
result.flowMatrix = flowMatrix.map(v => v.map(w => Math.max(0, w)))
result.edgesFlow = getEdges({matrix: result.flowMatrix});
} catch(e){result = e.message}
return result;
}
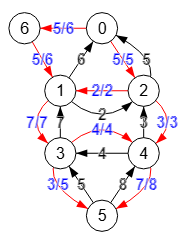
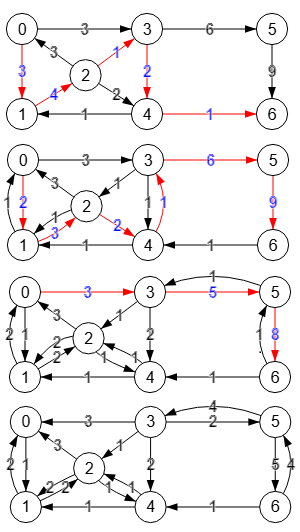
En la página de Wikipedia sobre el algoritmo de Edmonds–Karp encontramos el grafo de la Figura que nos servirá de base para explicar un poco el comportamiento del algoritmo.
Encontrar máximo flujo: {
"flow":5,
"residualMatrix":
[[0,1,0,0,0,0,0],
[2,0,2,0,0,0,0],
[3,2,0,0,1,0,0],
[3,0,1,0,2,2,0],
[0,1,1,0,0,0,0],
[0,0,0,4,0,0,5],
[0,0,0,0,1,4,0]],
"flowMatrix":
[[0,2,0,3,0,0,0],
[0,0,2,0,0,0,0],
[0,0,0,1,1,0,0],
[0,0,0,0,0,4,0],
[0,0,0,0,0,0,1],
[0,0,0,0,0,0,4],
[0,0,0,0,0,0,0]],
"edgesFlow":
{"0,1":2,"0,3":3,"1,2":2,
"2,3":1,"2,4":1,"3,5":4,
"4,6":1,"5,6":4}}Este es el resultado de encontrar el máximo flujo con valor 5 entre los nodos "0" y "6" usando como método de encontrar caminos el algoritmo findPath() de la aplicación, que a su vez se basa en la búsqueda en profundidad recursiva. Vemos el estado final de la matriz residual (residualMatrix), que al principio es una copia de la matriz de adyacencia del grafo original y sobre la que vamos buscando caminos entre el nodo fuente "0" y el sumidero "6".
Vamos a exponer como evoluciona la búsqueda de caminos sobre la matriz residual usando por un lado findPath y por otro el método de búsqueda de caminos mínimos de Dijkstra. Con el siguiente JSON puede importar el grafo de la Figura.
{"nodes":[
{"index":0,"nodeOffset":"7.5 3.5","parent":[{"index":-1},{"index":1,"value":3},{"index":3,"value":3}]},
{"index":1,"nodeOffset":"-5 37.5","parent":[{"index":-1},{"index":2,"value":4}]},
{"index":2,"nodeOffset":"7.9 22","parent":[{"index":-1},{"index":0,"value":3},{"index":3,"value":1},{"index":4,"value":2}]},
{"index":3,"nodeOffset":"20 3.5","parent":[{"index":-1},{"index":4,"value":2},{"index":5,"value":6}]},
{"index":4,"nodeOffset":"7.5 37.5","parent":[{"index":-1},{"index":1,"value":1},{"index":6,"value":1}]},
{"index":5,"nodeOffset":"45 3.5","parent":[{"index":-1},{"index":6,"value":9}]},
{"index":6,"nodeOffset":"32.5 37.5","parent":[{"index":-1}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find maximum flow",
"lastIndex":6
}}
El algoritmo para encontrar el máximo flujo es inicialmente de Ford–Fulkerson, aunque no definía que método usar para buscar esos caminos aumentados en la matriz residual. Un camino aumentado (augmenting path) en la matriz residual es un camino de flujo disponible desde la fuente al sumidero. Cuando ya no hayan más caminos aumentados disponibles en la matriz residual habremos alcanzado el máximo flujo.
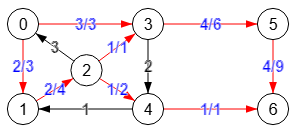
[0,1,2,3,4,6] [0,1,2,4,3,5,6] [0,3,5,6]
En la Figura se muestra como se van encontrando estos caminos usando findPath() en la matriz residual, que inicialmente es la matriz del grafo de partida, hasta que al final no hay más caminos entre el nodo fuente "0" y el sumidero "6", siendo el último grafo el correspondiente a la matriz residual final que se devuelve en el resultado, donde ya no hay camino posible entre "0" y "6".
Con cada camino buscamos la mínima capacidad, así en el primer camino es 1 (por ejemplo el de la arista "2🡒3)", en el segundo también es 1 (arista "4🡒2") y en el tercero es 3 (arista "0🡒3"), siendo la suma 1+1+3=5 el valor final del máximo flujo.
Encontrar máximo flujo: {
"flow":5,
"residualMatrix":
[[0,1,0,0,0,0,0],
[2,0,2,0,0,0,0],
[3,2,0,0,1,0,0],
[3,0,1,0,2,2,0],
[0,1,1,0,0,0,0],
[0,0,0,4,0,0,5],
[0,0,0,0,1,4,0]],
"flowMatrix":
[[0,2,0,3,0,0,0],
[0,0,2,0,0,0,0],
[0,0,0,1,1,0,0],
[0,0,0,0,0,4,0],
[0,0,0,0,0,0,1],
[0,0,0,0,0,0,4],
[0,0,0,0,0,0,0]],
"edgesFlow":
{"0,1":2,"0,3":3,"1,2":2,
"2,3":1,"2,4":1,"3,5":4,
"4,6":1,"5,6":4}}Usando el método de camino mínimo de Dijkstra obtenemos el mismo máximo flujo 5 que con findPath(). Y en este caso incluso la matriz residual y la de flujo son las mismas, algo que no tiene porque ser así tal como hemos visto en apartados anteriores. Aún así los caminos que se siguen son diferentes como veremos a continuación.
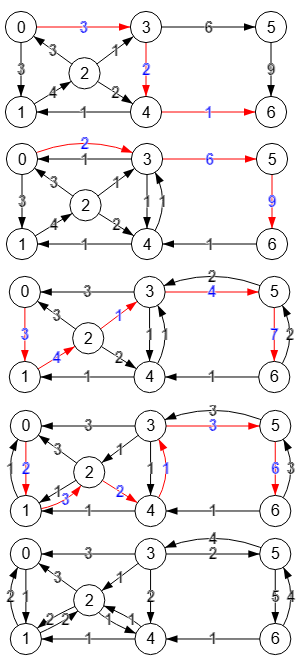
El algoritmo de Edmonds–Karp implementa el de Ford–Fulkerson buscando siempre el camino más corto. Aunque ese algoritmo parece que usa uno del tipo búsqueda en anchura, nosotros usaremos el algoritmo caminos mínimos de Dijkstra para ir encontrando esos caminos que vemos en la Figura.
El mínimo del primer camino 0,3,4,6 es 1, el del segundo 0,3,5,6 es 2, el del tercero 0,1,2,3,5,6 es 1, el del cuarto 0,1,2,4,3,5,6 es 1, siendo el máximo flujo la suma 1+2+1+1 =5.
Los caminos que hemos encontrado en la Figura coinciden con lo que expone la página de Wikipedia con el mismo ejemplo del algoritmo de Edmonds–Karp.
Encontrar caminos con aristas independientes usando máximo flujo findEdgeIndependentPathsMaxFlow()
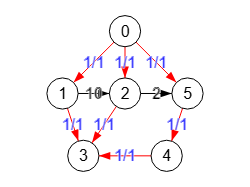
En el primer apartado vimos que podemos omitir pesos al ejecutar el algoritmo findMaximumFlow() para encontrar el máximo flujo.
0 7 9 0 0 14 0 0 10 15 0 0 0 0 0 11 0 2 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 9 0
En ese caso el algoritmo considera los pesos como unitarios, obteniendo el resultado que vemos en la Figura usando esta matriz de adyacencia ponderada inicial.
Encontrar máximo flujo:
{"flow":3,
"residualMatrix":
[[0,0,0,0,0,0],
[1,0,1,0,0,0],
[1,0,0,0,0,1],
[0,1,1,0,1,0],
[0,0,0,0,0,1],
[1,0,0,0,0,0]],
"flowMatrix":
[[0,1,1,0,0,1],
[0,0,0,1,0,0],
[0,0,0,1,0,0],
[0,0,0,0,0,0],
[0,0,0,1,0,0],
[0,0,0,0,1,0]],
"edgesFlow":
{"0,1":1,"0,2":1,"0,5":1,
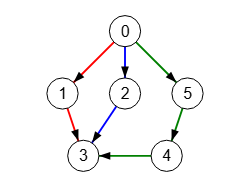
"1,3":1,"2,3":1,"4,3":1,"5,4":1}}El resultado del maximo flujo obtenido con findMaximumFlow() es "flow":3. Y precisamente al usar pesos unitarios esos 3 son también el número máximo de caminos con aristas independientes. Ya se intuyen en el grafo de flujo de la Figura esos 3 caminos con aristas independientes con vértices [0,1,3], [0,2,3] y [0,5,4,3].
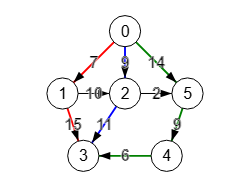
Así que findMaximumFlow() nos sirve para encontrar el máximo número de caminos con aristas indendientes en un grafo si utilizamos pesos unitarios, lo que aplicamos al algorimo findEdgeIndependentPathsMaxFlow() para encontrar ese número máximo. En la Figura lo vemos en ejecución, resaltándose en diferente color los 3 caminos encontrados, que es el máximo número de caminos con aristas independientes.
Encontrar caminos aristas independientes con máximo flujo: [[[0,1,3],[0,2,3],[0,5,4,3]]]
Este es el resultado obtenido que es el mismo que encontramos en el tema anterior con el algoritmo findIndependentPaths(), recordando que para este algoritmo había que especificar el número de caminos con aristas independientes que se querían encontrar, pues hay 6 caminos de tamaño 1, 7 de tamaño 2 y 1 de tamaño 3, no encontrándose más resultados a partir de 3 por lo que el tamaño máximo es 3. Con el nuevo algoritmo findEdgeIndependentPathsMaxFlow() no necesitaremos ir probando tamaños pues ya nos da el tamaño máximo.
En la Figura vemos la exportación a Wolfram, usando FindEdgeIndependentPaths[g, 1, 4, Infinity], que con "Infinity" encontrará el tamaño máximo con 3 caminos.
g = AdjacencyGraph[{{0,1,1,0,0,1},{0,0,1,1,0,0},{0,0,0,1,0,1},{0,0,0,0,0,0},{0,0,0,1,0,0},{0,0,0,0,1,0}},
ImageSize->188, VertexSize->{"Scaled", 0.1}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center]},
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(1->2)->7, (1->3)->9, (2->3)->10, (2->4)->15, (5->4)->6, (3->4)->11, (6->5)->9, (1->6)->14, (3->6)->2},
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindEdgeIndependentPaths[g, 1, 4, Infinity];
e = Table[EdgeList[PathGraph[i, DirectedEdges->True]], {i, f}];
c = {Red, Blue, RGBColor["green"], Yellow, Cyan, Orange, Pink, Magenta, Green, Brown, Purple, Gray, Black,
RGBColor["lavenderblush"], LightGreen, LightBlue, LightYellow, LightCyan, LightGray};
s = Table[Apply[Style,{i, Part[c, First[First[Position[e, i]]]], Thick}], {i,e}];
HighlightGraph[g, s]El código JavaScript para ejecutar findEdgeIndependentPathsMaxFlow() es el siguiente que usa findMaximumFlow() con el argumento omitWeigths: true para omitir pesos. Sobre la matriz de flujo obtenida aplicaremos findIndependentPaths() tomando la matriz de flujo y el tamaño oputSize: flow con valor de flujo 3 en el ejemplo visto antes.
function findEdgeIndependentPathsMaxFlow({matrix=[], firstIndex=0, lastIndex=0}) {
let result = [], temp;
try {
temp = findMaximumFlow({matrix, firstIndex, lastIndex, omitWeights:true});
if (typeof temp==="string") throw new Error(temp);
let flow = temp.flow;
let flowMatrix = temp.flowMatrix;
temp = findIndependentPaths({matrix:flowMatrix, firstIndex, lastIndex,
outputSize:flow, typeIndependence:"edge"});
if (typeof temp==="string") throw new Error(temp);
result = temp;
} catch(e){result = e.message}
return result;
}
Si con el grafo de la matriz de flujo (flowMatrix) que obtuvimos más arriba sobre el grafo inicial omitiendo pesos, aplicamos el algoritmo findIndependentPaths() con las opciones tamaño salida 3 y tipo independencia "arista" para encontrar los 3 caminos con aristas independientes, obtenemos el resultado de la Figura.
0 1 1 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0
Sobre esa matriz de flujo sin pesos actua el algoritmo findIndependentPaths() pasando el tamaño salida outputSize: 3 que se obtuvo desde findMaximumFlow(). De esta forma con findEdgeIndependentPathsMaxFlow() podemos encontrar el número máximo de caminos con aristas independientes en cualquier tipo de grafo, ponderado o no ponderado.