Corte de aristas en un grafo
Encontrar corte mínimo de aristas s-t findSTEdgeCut()
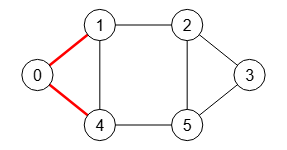
Un corte mínimo de aristas s-t supone encontrar un conjunto mínimo de aristas que separe los nodos "s" y "t" en distintos componentes conectados. En la Figura puede ver que para separar los nodos "0" y "3" en dos componentes necesariamente hay que eliminar subconjuntos de al menos 2 aristas, siendo sólo posible los tres resultados "0-1, 0-4", "1-2, 4-5" o "2-3, 5-3", eligiendo la aplicación el primero de ellos "0-1, 0-4". Es posible eliminar 3 aristas para ello, pero con 1 arista no lo conseguimos, con lo que 2 es el mínimo conjunto de aristas para conseguirlo.
Encontrar corte aristas s-t: [[0,1],[0,4]]
La aplicación devuelve el resultado con la lista de aristas [[0,1],[0,4]]. En este caso los dos componentes son [0] por un lado y [1, 2, 3, 4, 5] por otro, componentes que la aplicación no devuelve, pero que tras eliminar esas aristas "0-1" y "0-4", que podríamos hacer con operateEditionGraph(), podríamos obtener con el algoritmo getConnectedComponents() que vimos en el tema anterior:
operateEditionGraph({matrix, edges:[[0,1],[0,4]], edition:"delete"})
{"error":"", "matrix":
[[0,0,0,0,0,0],
[0,0,1,0,1,0],
[0,1,0,1,0,1],
[0,0,1,0,0,1],
[0,1,0,0,0,1],
[0,0,1,1,1,0]]
getConnectedComponents({matrix})
Componentes conectados:
[{"visited":[0],"path":[]},
{"visited":[1,2,3,5,4],"path":[[1,2],[2,3],[3,5],[5,4]]}]El término mínimo en la definición se refiere a que el algoritmo selecciona el subconjunto de aristas que tenga menor peso en total cuando el grafo es ponderado. Si no lo es, como pasa con este ejemplo, se entiende que las aristas tienen peso unitario, por lo que cualquiera de las tres posibilidades "0-1, 0-4", "1-2, 4-5" o "2-3, 5-3" podría ser un corte mínimo de aristas válido, todos con peso 1+1=2.
{"nodes":[
{"index":0,"nodeOffset":"-35 17.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"6.67 -27.5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"25 -52.5","parent":[{"index":1}]},
{"index":3,"nodeOffset":"66.67 -57.5","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-26.67 12.5","parent":[{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"8.33 -37.5","parent":[{"index":2},{"index":3},{"index":4}]}
],
"config":{
"algorithm":"Find s-t edge cut",
"lastIndex":3
}}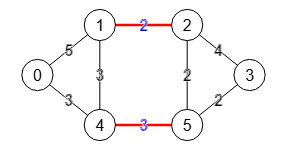
En la Figura vemos el mismo grafo ponderado, observando que el algoritmo opta por el subconjunto "1-2, 4-5" pues la suma de sus pesos 2+3=5 es menor que las otras posibilidades "0-1, 0-4" con peso 5+3=8 o "2-3, 5-3" con peso 4+2=6.
{"nodes":[
{"index":0,"nodeOffset":"-35 17.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"6.67 -27.5","parent":[{"index":0,"value":5}]},
{"index":2,"nodeOffset":"25 -52.5","parent":[{"index":1,"value":2}]},
{"index":3,"nodeOffset":"66.67 -57.5","parent":[{"index":2,"value":4}]},
{"index":4,"nodeOffset":"-26.67 12.5","parent":[{"index":0,"value":3},{"index":1,"value":3}]},
{"index":5,"nodeOffset":"8.33 -37.5","parent":[{"index":2,"value":2},{"index":3,"value":2},{"index":4,"value":3}]}
],
"config":{
"algorithm":"Find s-t edge cut",
"lastIndex":3
}}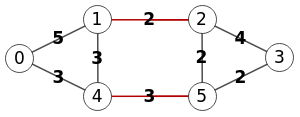
En la Figura vemos que Wolfram alcanza el mismo resultado. Usa la función FindEdgeCut[g,1,4] recordando que "s=1" y "t=4" se corresponden con "0" y "3" pues los índices en Wolfram se inician en 1.
g = WeightedAdjacencyGraph[{{∞,5,∞,∞,3,∞},{5,∞,2,∞,3,∞},{∞,2,∞,4,∞,2},{∞,∞,4,∞,∞,2},{3,3,∞,∞,∞,3},{∞,∞,2,2,3,∞}},
ImageSize->300, VertexSize->{"Scaled", 0.1}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center]},
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(2->1)->5, (3->2)->2, (4->3)->4, (5->1)->3, (5->2)->3, (6->3)->2, (6->4)->2, (6->5)->3},
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
e = FindEdgeCut[g, 1, 4];
HighlightGraph[g, e]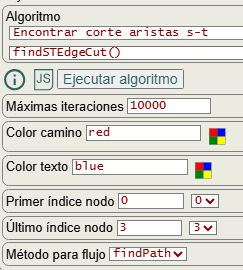
En las opciones para ejecutar el algoritmo findSTEdgeCut() que encuentra un corte mínimo "s-t" de aristas que vemos en la Figura están primer índice nodo y último índice nodo para "s" y "t" respectivamente. Las opciones color camino y color texto para resaltar las aristas y su texto no forman parte de la ejecución del algoritmo, pues se aplican al resultado obtenido para presentar en pantalla las aristas de corte.
La opción método para flujo puede ser "findPath", "dijkstra" y "floyd", usándose respectivamente los algoritmos findPath() para encontrar caminos entre dos nodos, caminos mínimos de Dijkstra y caminos mínimos de Floyd. Los dos últimos son más eficientes para grafos con muchos nodos y aristas.
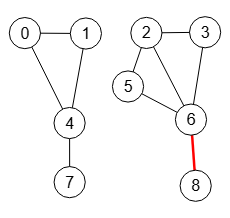
Para encontrar el corte mínimo de aristas s-t no es necesario que el grafo esté conectado, sólo se necesita que haya una camino entre el nodo "s" y el nodo "t". En la Figura vemos un grafo desconectado con el corte de aristas entre nodos "2" y "8" resultando la arista "6-8".
Si intentáramos el corte entre "0" y "8", donde no hay camino, no acusaría error y simplemente devolvería un resultado vacío.
{"nodes":[
{"index":0,"nodeOffset":"-23.36 0.77","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"17.74 -24.06","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-8.02 0.71","parent":[{"index":-1}]},
{"index":3,"nodeOffset":"48.85 -24.57","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-22.12 11.84","parent":[{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"-15.38 -2.81","parent":[{"index":2}]},
{"index":6,"nodeOffset":"-6.81 10.47","parent":[{"index":2},{"index":3},{"index":5}]},
{"index":7,"nodeOffset":"-5.42 10.54","parent":[{"index":4}]},
{"index":8,"nodeOffset":"11.73 11.99","parent":[{"index":6}]}
],
"config":{
"algorithm":"Find s-t edge cut",
"firstIndex":2,
"lastIndex":8
}}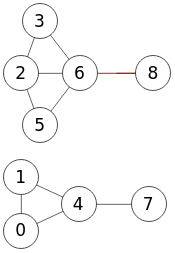
En la Figura vemos el mismo resultado en Wolfram del ejemplo anterior. Aunque en la referencia de Wolfram FindEdgeCut] dice que para un grafo desconectado FindEdgeCut devolverá una lista vacía {}, sin embargo en este ejemplo no es así devolviendo la arista 7-9 que se corresponde con 6-8 de nuestra aplicación.
g = AdjacencyGraph[{{0,1,0,0,1,0,0,0,0},{1,0,0,0,1,0,0,0,0},{0,0,0,1,0,1,1,0,0},{0,0,1,0,0,0,1,0,0},{1,1,0,0,0,0,0,1,0},
{0,0,1,0,0,0,1,0,0},{0,0,1,1,0,1,0,0,1},{0,0,0,0,1,0,0,0,0},{0,0,0,0,0,0,1,0,0}}, ImageSize->175,
VertexSize->{"Scaled", 0.14}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center], 7->Placed[6,Center], 8->Placed[7,Center],
9->Placed[8,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
e = FindEdgeCut[g, 3, 9];
HighlightGraph[g, e]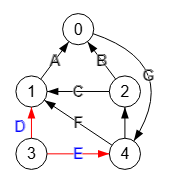
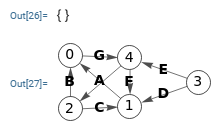
Para el grafo dirigido de la Figura vemos el corte de aristas entre nodos "3" y "0" observando que resultan las aristas "3-1" y "3-4" de tal forma que eliminando esas aristas tendremos el "3" y el "0" en dos componentes conectados distintos.
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4,"value":"G","lineOffset":"6 -2","lineType":"quadratic"}]},
{"index":1,"parent":[{"index":0,"value":"A"}]},
{"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"C"}]},
{"index":3,"parent":[{"index":1,"value":"D","lineTextOffset":"-0.75 0.25"},{"index":4,"value":"E"}]},
{"index":4,"parent":[{"index":1,"value":"F"},{"index":2}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find s-t edge cut",
"firstIndex":3
}}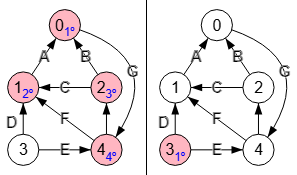
En la Figura vemos los componentes fuertemente conectados del grafo anterior, observando que ya los nodos "3" y "0" están en dos componentes, por lo que la eliminación de las aristas "3-1" y "3-4" los deja en esos dos componentes.
Recordemos que un componente es fuertemente conectado en un grafo dirigido si desde cualquier nodo del componente podemos llegar a otro cualquiera en el mismo componente.
| s-t | edges cut |
|---|---|
| [0,1],[0,2],[0,4],[2,4] | [[0,4]] |
| [1,0],[1,2],[1,4] | [[1,0]] |
| [3,2],[4,2] | [[4,2]] |
| [2,0],[2,1] | [[2,0],[2,1]] |
| [3,0],[3,1],[3,4] | [[3,1],[3,4]] |
| [4,0],[4,1] | [[4,1],[4,2]] |
| [0,3],[1,3],[2,3],[4,3] | [] |
Cuando veamos en un próximo apartado el algoritmo findEdgeCut() que encuentra todas las aristas de corte, veremos que para ese grafo obtendremos este resultado puesto en forma de tabla.
En la primera columna están todas las combinaciones de "s" y "t" y en la segunda columna las aristas de corte. Vemos en la quinta columna "s=3, t=0" con el resultado que ya vimos con las aristas de corte "3-1" y "3-4", obteniéndose los dos componentes fuertemente conectados [3] y [0,1,2,4] estando "s=3" en un componente y "t=0" en otro, como vemos en la Figura. Si vemos otro caso como "s=0", "t=1" con arista de corte "0-4", si eliminamos esta arista en el grafo obtendremos los componentes fuertemente conectados [0], [1], [2], [3] y [4], uno por cada nodo, de tal forma que "s=0" estará en un componente y "t=1" en otro.
Es por eso que en la definición inicial decíamos Un corte mínimo de aristas s-t supone encontrar un conjunto mínimo de aristas que separe los nodos "s" y "t" en distintos componentes conectados
.
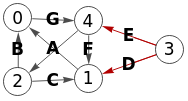
En la Figura vemos el mismo resultado en Wolfram.
g = WeightedAdjacencyGraph[{{∞,∞,∞,∞,1},{1,∞,∞,∞,∞},{1,1,∞,∞,∞},{∞,1,∞,∞,1},{∞,1,1,∞,∞}}, ImageSize->188,
VertexSize->{"Scaled", 0.17}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], EdgeLabels->{(1->5)->"G", (2->1)->"A", (3->1)->"B", (3->2)->"C",
(4->2)->"D", (4->5)->"E", (5->2)->"F"}, VertexStyle->White, DirectedEdges->True,
EdgeStyle->{{Black,Thickness[0.005]}}];
e = FindEdgeCut[g, 4, 1];
HighlightGraph[g, e]Algoritmo findSTEdgeCut()
Este es el código JavaScript del algoritmo findSTEdgeCut() que explicaremos a continuación.
function findSTEdgeCut({matrix=[], firstIndex=0, lastIndex=0}) {
let result = [], temp;
try {
let path = findPath({matrix, firstIndex, lastIndex});
if (typeof path==="string") throw new Error(path);
if (path.length>0) {
let n = matrix.length;
if (firstIndex===lastIndex) throw new Error(`First index and last index are equal`);
if (firstIndex<0 || firstIndex>=n) throw new Error(`First index is wrong`);
if (lastIndex<0 || lastIndex>=n) throw new Error(`Last index is wrong`);
temp = findMaximumFlow({matrix, firstIndex, lastIndex});
if (typeof temp==="string") throw new Error(temp);
let residualMatrix = temp.residualMatrix;
let visited = [firstIndex];
for (let j=0; j<n; j++) {
if (j!==firstIndex) {
temp = findPath({matrix:residualMatrix, firstIndex, lastIndex:j});
if (typeof temp==="string") throw new Error(temp);
if (temp.length>0 && !visited.includes(j)){
visited.push(j);
}
}
}
for (let i=0; i<n; i++) {
for (let j=0; j<n; j++) {
if (matrix[i][j]>0 && visited.includes(i) && !visited.includes(j)){
result.push([i, j]);
}
}
}
}
} catch(e){result = e.message}
return result;
}En primer lugar vemos si hay un camino entre "s" (firstIndex) y "t" (lastIndex) usando el algoritmo findPath() que encuentra todos los caminos entre dos nodos. Si no lo hay no tiene sentido encontrar aristas de corte para separar los nodos "s" y "t", pues ya estarán en dos componentes conectados distintos.
Vemos que se utiliza el algoritmo findMaximumFlow() para encontrar el máximo flujo entre los nodos "s" y "t". Se suele identificar "s" como fuente y "t" como sumidero.
El teorema de Menger para la conectividad de aristas dice que para dos vértices distintos "s" y "t" el número máximo de caminos independientes es igual que el mínimo número de aristas que es necesario eliminar para separar esos vértices "s" y "t" en componentes distintos. Y el teorema del máximo flujo y mínimo corte establece que la máxima cantidad de flujo que va de la fuente "s" al sumidero "t" es igual que el mínimo corte necesario para desconectar "s" y "t". Así que:
Con esta base aplicamos el algoritmo de máximo flujo para encontrar caminos con aristas independientes en un tema anterior. Y ahora lo aplicamos para encontrar el corte mínimo de aristas.
Para encontrar ese conjunto de aristas de corte mínimo usaremos la matriz residual (residualMatrix) que el algoritmo findMaximumFlow() también devuelve.

Veamos esto con un ejemplo. En la Figura vemos el corte mínimo de aristas en un grafo ponderado, que ya expusimos en el apartado anterior en la Figura, corte mínimo entre nodos "0" y "3" obteniendo las aristas "1-2" y "4-3" con peso mínimo 3+2=5.
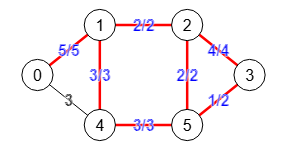
En la Figura vemos el flujo máximo de ese grafo ejecutando findMaximumFlow() entre nodos "0" y "3". Recuerde que las etiquetas como "1/2" de la arista "5-3" significa que esa arista tiene una capacidad 2 y utiliza un flujo 1, por lo que aún sobra 1 capacidad.
Encontrar máximo flujo: {
"flow":5,
"residualMatrix":
[[0,0,0,0,3,0],
[10,0,0,0,0,0],
[0,4,0,0,0,4],
[0,0,8,0,0,3],
[3,6,0,0,0,0],
[0,0,0,1,6,0]],
"flowMatrix":
[[0,5,0,0,0,0],
[0,0,2,0,3,0],
[0,0,0,4,0,0],
[0,0,0,0,0,0],
[0,0,0,0,0,3],
[0,0,2,1,0,0]],
"edgesFlow":
{"0,1":5,"1,2":2,"1,4":3,
"2,3":4,"4,5":3,"5,2":2,
"5,3":1}}
Se obtiene este resultado donde vemos que el flujo máximo es "flow":5 valor que para las aristas "1-2" y "4-5" de la Figura coincide con la suma de sus pesos (o capacidades en este caso) 2+3=5.
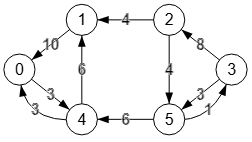
En la Figura vemos el grafo residual a partir de la matriz residual. Recuerde que encontrar el máximo flujo siempre se aplica sobre grafos dirigidos, pues se basa en una red de flujo entre la fuente y el sumidero. Cuando el grafo es no dirigido, como en este ejemplo, el algoritmo entenderá cada arista no dirigida "u-v" como "u🡒v" y su opuesta "v🡒u", ambas con la misma capacidad que tiene la no dirigida.
Observe por ejemplo que la arista "0🡘1" en la Figura con capacidad 5 utiliza toda su capacidad 5/5 como se observa en Figura, de ahí que en la Figura del grafo residual sólo haya una arista "1🡒0" en el sentido sumidero a fuente. Mientras que la arista "0🡘4" no se utiliza en el flujo, por lo que permanece en el grafo residual como al inicio "0🡘4".
Para encontrar el corte mínimo de aristas iteramos en el grafo residual encontrando todo aquellos nodos que puedan alcanzarse desde el nodo fuente "s", observando que, aparte del propio nodo "0" puede alcanzar sólo los nodos "1" y "4". Con esta lista de nodos visitados [0, 1, 4]
0 1 2 3 4 5 0 0 5 0 0 3 0 1 5 0 2 0 3 0 2 0 2 0 4 0 2 3 0 0 4 0 0 2 4 3 3 0 0 0 3 5 0 0 2 2 3 0
Con esa lista de nodos visitados visited = [0, 1, 4] comprobamos en la matriz de adyacencia del grafo inicial aquellas posiciones [i, j] tal que matrix[i][j]>0 y visited.includes(i) y !visited.includes(j). Solo cabe la posición [1, 2] con valor 5 pues i=1 está en los visitados y j=2 no está en los visitados. Y la posición [4, 5] con valor 3 pues i=4 está en los visitados y j=5 no está en los visitados.
Aunque en el algoritmo iteramos por todos los nodos, también podríamos haber obtenido una lista de aristas [[0,1], [0,4], [1,2], [1,4], [2,3], [2,5], [3,5], [4,5]] observando que sólo las resaltadas en azul cumplen los criterios, pues las aristas [0,1], [0,4] y [1,4] tienen ambos "i" y "j" en los visitados, mientras que para [2,3], [2,5] y [3,5] ningún "i" o "j" están en los visitados.
Observe que esto nos dice los componentes, pues uno lo forma [[0,1],[0,4],[1,4]] incluyendo la fuente "0", otro lo forma [[2,3],[2,5],[3,5]] incluyendo el sumidero "3" y finalmente el resto de aristas [[1,2],[4,5]] conforman el conjunto mínimo de corte.
Encontrar corte de aristas findEdgeCut()
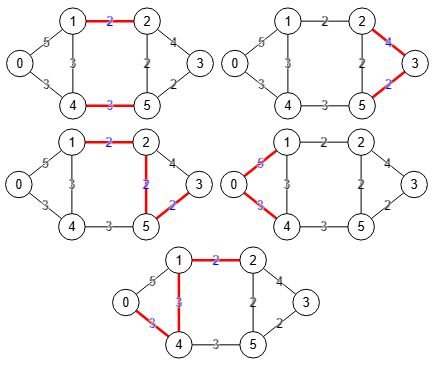
Encontrar todos los cortes de aristas supone iterar por todas las parejas de nodos "u" y "v" encontrando las aristas que producen un corte mínimo y finalmente devolver todos los resultados ordenados por la suma de flujos creciente, siendo el primer resultado la solución con mínimo corte. Usamos findSTEdgeCut() que encuentra el corte mínimo de aristas entre dos nodos "s" y "t".
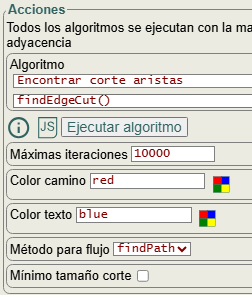
En la Figura vemos todos los cortes de aristas en un grafo no dirigido ponderado. Siempre la primera solución es la de corte mínimo, pues se observa que la suma de los pesos o capacidades para las aristas "1-2" y "4-5" es 2+3=5, menor que las sumas de las otras soluciones 6, 6, 8 y 8. Se obtiene el siguiente resultado:
Encontrar corte aristas: {
"edges":[[[1,2],[4,5]],
[[2,3],[3,5]],
[[1,2],[2,5],[3,5]],
[[0,1],[0,4]],
[[0,4],[1,2],[1,4]]],
"st":[[[0,2],[0,3],[0,5],[1,2],[1,3],[1,5],[2,4],[3,4],[4,5]],
[[2,3],[3,5]],
[[2,5]],
[[0,1],[0,4]],
[[1,4]]],
"stEmpty":[],
"warnings":[]
}En "edges" tenemos las cinco aristas de corte ordenadas por suma de flujos creciente. En "st" tenemos todas las combinaciones de parejas "s" y "t" cuyo ordenamiento se corresponde con el de las aristas, así que podríamos presentarlo en una tabla como la siguiente:
| s-t | edges cut |
|---|---|
| [[0,2],[0,3],[0,5], [1,2],[1,3],[1,5], [2,4],[3,4],[4,5]] | [[1,2],[4,5]] |
| [[2,3],[3,5]] | [[2,3],[3,5]] |
| [[2,5]] | [[1,2],[2,5],[3,5]] |
| [[0,1],[0,4]] | [[0,1],[0,4]] |
| [[1,4]]] | [[0,4],[1,2],[1,4]] |
En "stEmpty" apareceran aquellas parejas de nodos "u" y "v" donde no existe un camino entre ellos, algo que sólo puede darse un un grafo desconectado estando "s" y "t" en dos componentes distintos. En "warnings" aparacerán avisos que explicaremos cuando expongamos el JavaScript de findEdgeCut() al final de este apartado.
Observe que para la arista "u-v" en un grafo no dirigido existe a efecto del máximo flujo la arista "u🡒v" y su opuesta "v🡒u", ambas con la misma capacidad. Pero aquí consideramos sólo las aristas en forma compacta, de tal forma que cuando se nos da la arista no dirigida "u-v" codificada como [u, v] es porque u≤v.
{"nodes":[
{"index":0,"nodeOffset":"-35 17.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"6.67 -27.5","parent":[{"index":0,"value":5}]},
{"index":2,"nodeOffset":"25 -52.5","parent":[{"index":1,"value":2}]},
{"index":3,"nodeOffset":"66.67 -57.5","parent":[{"index":2,"value":4}]},
{"index":4,"nodeOffset":"-26.67 12.5","parent":[{"index":0,"value":3},{"index":1,"value":3}]},
{"index":5,"nodeOffset":"8.33 -37.5","parent":[{"index":2,"value":2},{"index":3,"value":2},{"index":4,"value":3}]}
],
"config":{
"lineHeight":21.25,
"algorithm":"Find edge cut"
}}
En la Figura vemos la opción mínimo tamaño corte que se pasa al algoritmo findEdgeCut(), opción que explicaremos a continuación. Las otras opciones color camino y color texto se aplican posteriormente al obtener el resultado del algoritmo.
La opción método para flujo puede ser "findPath", "dijkstra" y "floyd", usándose respectivamente los algoritmos findPath() para encontrar caminos entre dos nodos, caminos mínimos de Dijkstra y caminos mínimos de Floyd. Los dos últimos son más eficientes para grafos con muchos nodos y aristas.
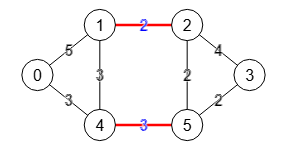
Si marcamos la opción mínimo tamaño de corte el algoritmo devolverá aquella solución cuya suma de pesos sea mínima. Para el ejemplo de la Figura se devuelve la primera solución con las aristas [[1,2],[4,5]] tal como se muestra en el grafo y resultado obtenido siguiente:
Encontrar corte aristas: {
"edges":[[[1,2],[4,5]]],
"st":[[[0,2],[0,3],[0,5],[1,2],
[1,3],[1,5],[2,4],[3,4],[4,5]]],
"stEmpty":[],
"warnings":[]}}
{"nodes":[
{"index":0,"nodeOffset":"-35 17.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"6.67 -27.5","parent":[{"index":0,"value":5}]},
{"index":2,"nodeOffset":"25 -52.5","parent":[{"index":1,"value":2}]},
{"index":3,"nodeOffset":"66.67 -57.5","parent":[{"index":2,"value":4}]},
{"index":4,"nodeOffset":"-26.67 12.5","parent":[{"index":0,"value":3},{"index":1,"value":3}]},
{"index":5,"nodeOffset":"8.33 -37.5","parent":[{"index":2,"value":2},{"index":3,"value":2},{"index":4,"value":3}]}
],
"config":{
"lineHeight":21.25,
"algorithm":"Find edge cut",
"minimumSizeCut":true
}}Siendo λ(u, v) el mínimo número de aristas que separa los vértices "u" y "v" y λ(G) el mínimo número de aristas que es necesario eliminar para desconectar el grafo "G", entonces como consecuencia del teorema de Menger y del máximo flujo y mínimo corte, dice que λ(G) es el mínimo λ(u, v) sobre todas las parejas de distintos vértices "u" y "v" adyacentes o no. Por lo tanto cuando marcamos la opción mínimo tamaño corte estaremos aplicando estos conceptos, pues como veremos después en el código del algoritmo, iteramos por todas las parejas de nodos encontrando todos los flujos máximos y al final buscaremos el primer conjunto de aristas con menor flujo.
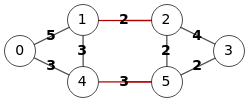
En la Figura vemos el mismo resultado en Wolfram usand FindEdgeCut[g]. Con esta función sólo hay dos posibilidades, o bien usar FindEdgeCut[g, s, t] para encontrar un corte mínimo de aristas entre "s" y "t" que vimos en el apartado anterior, o bien usar FindEdgeCut[g] sin "s" y "t" para encontrar un corte mínimo del grafo, como hacemos ahora. No hay opción para obtener todos los cortes de aristas, siempre devuelve un único corte mínimo.
g = WeightedAdjacencyGraph[{{∞,5,∞,∞,3,∞},{5,∞,2,∞,3,∞},{∞,2,∞,4,∞,2},{∞,∞,4,∞,∞,2},{3,3,∞,∞,∞,3},{∞,∞,2,2,3,∞}},
ImageSize->250, VertexSize->{"Scaled", 0.14}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center]}, VertexLabelStyle->Directive[Black,14.88],
EdgeLabelStyle->Directive[Black,14.88,Bold], EdgeLabels->{(2->1)->5, (3->2)->2, (4->3)->4, (5->1)->3, (5->2)->3, (6->3)->2, (6->4)->2, (6->5)->3},
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
e = FindEdgeCut[g];
HighlightGraph[g, e]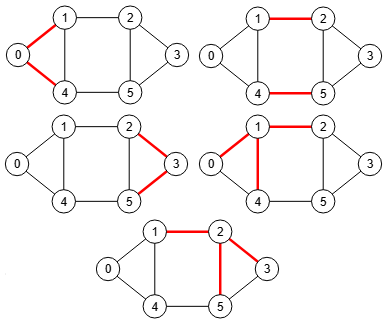
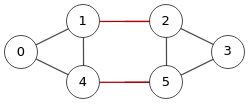
Para el mismo grafo pero sin pesos, en la Figura vemos los cortes de aristas, donde los de tamaño 2 son iguales que los vistos en el ejemplo ponderado anterior (Figura) pero los de tamaño 3 son distintos, con este resultado:
Encontrar corte aristas: {
"edges":[[[0,1],[0,4]],
[[1,2],[4,5]],
[[2,3],[3,5]],
[[0,1],[1,2],[1,4]],
[[1,2],[2,3],[2,5]]],
"st":[[[0,1],[0,2],[0,3],[0,4],[0,5]],
[[1,2],[1,3],[1,5],[2,4],[4,5]],
[[2,3],[3,4],[3,5]],
[[1,4]],
[[2,5]]],
"stEmpty":[],
"warnings":[]}| s-t | edges cut |
|---|---|
| [0,1],[0,2],[0,3],[0,4],[0,5] | [[0,1],[0,4]] |
| [1,2],[1,3],[1,5],[2,4],[4,5] | [[1,2],[4,5]] |
| [2,3],[3,4],[3,5] | [[2,3],[3,5]] |
| [1,4] | [[0,1],[1,2],[1,4]] |
| [2,5] | [[1,2],[2,3],[2,5]] |
Con el resultado anterior puesto en forma de tabla vemos todos los "s-t" que producen los cortes de aristas.
{"nodes":[
{"index":0,"nodeOffset":"-35 17.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"6.67 -27.5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"25 -52.5","parent":[{"index":1}]},
{"index":3,"nodeOffset":"66.67 -57.5","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-26.67 12.5","parent":[{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"8.33 -37.5","parent":[{"index":2},{"index":3},{"index":4}]}
],
"config":{
"lineHeight":18.75,
"algorithm":"Find edge cut"
}}
En Wolfram sólo se obtiene siempre un único corte mínimo con FindEdgeCut[g], como el que vemos en la Figura igual que el segundo de la Figura que obtuvimos en nuetra aplicación.
g = AdjacencyGraph[{{0,1,0,0,1,0},{1,0,1,0,1,0},{0,1,0,1,0,1},{0,0,1,0,0,1},{1,1,0,0,0,1},{0,0,1,1,1,0}},
ImageSize->250, VertexSize->{"Scaled", 0.15}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center]},
VertexLabelStyle->Directive[Black,13.13], EdgeLabelStyle->Directive[Black,13.13,Bold],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
e = FindEdgeCut[g];
HighlightGraph[g, e]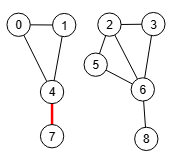
En el primer apartado del algoritmo findSTEdgeCut() para encontrar el corte mínimo de aristas s-t se definía como la acción de encontrar un conjunto mínimo de aristas que separe los nodos "s" y "t" en distintos componentes conectados. En ningún caso esta definición limita a que el grafo esté o no conectado. El algoritmo findEdgeCut() que veremos después itera por todas las parejas de nodos "s" y "t" aplicando findSTEdgeCut() para encontrar el mínimo de los cortes "s-t" que será el mínimo corte del grafo, como explicamos antes. Así que esto tampoco limita su aplicación a grafos desconectados.
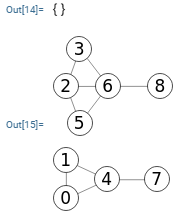
En la Figura vemos un grafo desconectado donde aplicamos findEdgeCut() con la opción mínimo tamaño corte activada, encontrando el primer corte mínimo en la arista [4, 7].
Encontrar corte aristas: {
"edges":[[[4,7]]],
"st":[[[0,7],[1,7],[4,7]]],
"stEmpty":[[0,2],[0,3],[0,5],[0,6],
[0,8],[1,2],[1,3],[1,5],[1,6],
[1,8],[2,4],[2,7],[3,4],[3,7],
[4,5],[4,6],[4,8],[5,7],[6,7],[7,8]],
"warnings":[]}En "st" vemos todas la parejas del primer componente conectado. En "stEmpty" vemos todas las parejas "s" y "t" que están en componentes distintos, no existiendo por tanto un camino entre ellos.
{"nodes":[
{"index":0,"nodeOffset":"-23.36 0.77","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"17.74 -24.06","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-8.02 0.71","parent":[{"index":-1}]},
{"index":3,"nodeOffset":"48.85 -24.57","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-22.12 11.84","parent":[{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"-15.38 -2.81","parent":[{"index":2}]},
{"index":6,"nodeOffset":"-6.81 10.47","parent":[{"index":2},{"index":3},{"index":5}]},
{"index":7,"nodeOffset":"-5.42 10.54","parent":[{"index":4}]},
{"index":8,"nodeOffset":"11.73 11.99","parent":[{"index":6}]}
],
"config":{
"lineHeight":18.75,
"algorithm":"Find edge cut",
"minimumSizeCut":true
}}
La referencia de Wolfram FindEdgeCut dice que para un grafo desconectado devolverá una lista vacía {}. Pero ya vimos un ejemplo en la Figura con FindEdgeCut[g, s, t] donde eso no se cumplía, pues aplicado al mismo grafo que estamos ahora usando encontraba un resultado. Sin embargo ahora con FindEdgeCut[g] sin argumentos "s" y "t" parece que si está considerando que el grafo está desconectado pues devuelve una lista vacía {}.
g = AdjacencyGraph[{{0,1,0,0,1,0,0,0,0},{1,0,0,0,1,0,0,0,0},{0,0,0,1,0,1,1,0,0},{0,0,1,0,0,0,1,0,0},
{1,1,0,0,0,0,0,1,0},{0,0,1,0,0,0,1,0,0},{0,0,1,1,0,1,0,0,1},{0,0,0,0,1,0,0,0,0},{0,0,0,0,0,0,1,0,0}},
ImageSize->164, VertexSize->{"Scaled", 0.14}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center], 7->Placed[6,Center],
8->Placed[7,Center], 9->Placed[8,Center]}, VertexLabelStyle->Directive[Black,13.13],
EdgeLabelStyle->Directive[Black,13.13,Bold], VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
e = FindEdgeCut[g];
HighlightGraph[g, e]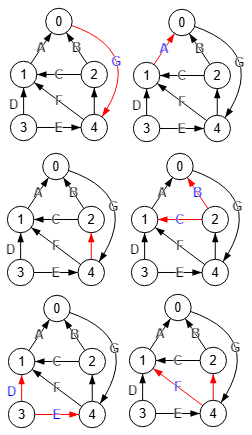
En la Figura encontramos todos los cortes de aristas en un grafo dirigido, con este resultado:
Encontrar corte aristas: {
"edges":[[[0,4]],
[[1,0]],
[[4,2]],
[[2,0],[2,1]],
[[3,1],[3,4]],
[[4,1],[4,2]]],
"st":[[[0,1],[0,2],[0,4],[2,4]],
[[1,0],[1,2],[1,4]],
[[3,2],[4,2]],
[[2,0],[2,1]],
[[3,0],[3,1],[3,4]],
[[4,0],[4,1]]],
"stEmpty":[[0,3],[1,3],[2,3],[4,3]],
"warnings":[]}| s-t | edges cut |
|---|---|
| [0,1],[0,2],[0,4],[2,4] | [[0,4]] |
| [1,0],[1,2],[1,4] | [[1,0]] |
| [3,2],[4,2] | [[4,2]] |
| [2,0],[2,1] | [[2,0],[2,1]] |
| [3,0],[3,1],[3,4] | [[3,1],[3,4]] |
| [4,0],[4,1] | [[4,1],[4,2]] |
| [0,3],[1,3],[2,3],[4,3] | [] |

Este grafo dirigido está desconectado, con dos componentes fuertemente conectados que vemos en la Figura. Los cortes de aristas de tamaño 1 son "0🡒4", "1🡒0" y "4🡒2", observando que eliminando cualquiera de estas aristas deshace el primer componente pues ya no tendremos acceso entre nodos de ese subconjunto [0,1,2,4], pasando el número de componentes de 2 a 5.
De igual forma para los cortes de tamaño 2 como "2🡒0, 2🡒1" y "4🡒1, 4🡒2" al eliminar esas aristas desconectamos el primer componente. Podría ser incluso innecesario recopilar en el resultado el corte "3🡒1, 3🡒4", pues ya el nodo "3" está en un componente distinto al resto.
Como el grafo está desconectado, vemos en el resultado "stEmpty" todas las parejas de nodos entre los que no hay un camino que son [0,3],[1,3],[2,3],[4,3].
Ya vimos que la función FindEdgeCut[g] en Wolfram dice que para grafos desconectados se devolverá un resultado vacío. Y parace que lo aplica a este caso pues devuelve {} al estar el grafo desconectado, lo que puede comprobar con la función ConnectedGraphQ[g] devolviendo falso.
g = WeightedAdjacencyGraph[{{∞,∞,∞,∞,1},{1,∞,∞,∞,∞},{1,1,∞,∞,∞},{∞,1,∞,∞,1},{∞,1,1,∞,∞}}, ImageSize->159,
VertexSize->{"Scaled", 0.17}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,14.88],
EdgeLabelStyle->Directive[Black,14.88,Bold], EdgeLabels->{(1->5)->"G", (2->1)->"A", (3->1)->"B", (3->2)->"C",
(4->2)->"D", (4->5)->"E", (5->2)->"F"}, VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
e = FindEdgeCut[g]
HighlightGraph[g, e]Veamos ahora el JavaScript del algoritmo findEdgeCut():
function findEdgeCut({matrix=[], minimumSizeCut=false}) {
let result = {edges: [], st: [], stEmpty: []}, temp;
result.warnings = [];
try {
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
temp = getMatrixModeValue({matrix});
if (typeof temp==="string") throw new Error (temp);
let [modeValue, nullValue] = temp;
let n = matrix.length;
let sets = new Set();
let sts = {};
let stsEmpty = [];
for (let firstIndex=0; firstIndex<n; firstIndex++) {
let from = directed ? 0 : firstIndex+1;
let br = false;
for (let lastIndex=from; lastIndex<n; lastIndex++) {
if (firstIndex!==lastIndex) {
let path = findPath({matrix, firstIndex, lastIndex});
if (typeof path==="string") throw new Error(path);
if (path.length===0) {
result.stEmpty.push([firstIndex, lastIndex]);
} else {
if (iter++, iter>maxIter) {
result.warnings.push([`Maximum iterations '${maxIter}' reached` +
` testing s=${firstIndex} t=${lastIndex}`]);
br = true;
break;
}
temp = findSTEdgeCut({matrix, firstIndex, lastIndex});
if (typeof temp==="string") {
result.warnings.push("(findSTEdgeCut) " + temp +
` testing s=${firstIndex} t=${lastIndex}`);
} else {
let edges = temp;
if (!directed) {
edges = edges.map(v => v.toSorted((x,y) => x-y));
}
let edgesStr = JSON.stringify(edges);
sets.add(edgesStr);
if (!sts.hasOwnProperty(edgesStr)) sts[edgesStr] = [];
sts[edgesStr].push([firstIndex, lastIndex]);
}
}
}
}
if (br) break;
}
if (sets.size>0) {
sets = [...sets].map(v => JSON.parse(v));
if (modeValue==="0/number") {
sets.sort((u,v) => {
let s1 = u.reduce((p,w) => (p+=matrix[w[0]][w[1]], p), 0);
let s2 = v.reduce((p,w) => (p+=matrix[w[0]][w[1]], p), 0);
return s1-s2;
});
} else {
sets.sort((u,v) => u.length-v.length);
}
if (minimumSizeCut) {
result.edges.push(sets[0]);
} else {
result.edges.push(...sets);
}
result.st = Array.from({length: result.edges.length}, ()=>null);
for (let st of Object.keys(sts)) {
let k = result.edges.findIndex(v => JSON.stringify(v)===st);
if (k>-1) result.st[k] = sts[st];
}
}
} catch(e){result = e.message}
return result;
}Se usan las siguientes funciones:
isGraphDirected()para saber si el grafo es dirigido.getMatrixModeValue()para obtener el modo valores de la matriz.findPath()que encuentra todos los caminos entre dos nodos.
El funcionamiento es iterar por todas las parejas de nodos del grafo firstIndex y lastIndex. Si el grafo es no dirigido podemos limitar el segundo bucle con let from = directed ? 0 : firstIndex+1 pues la matriz de adyacencia será simétrica respecto a la diagonal derecha, sobre lo cual ya hablamos más arriba diciendo que este algoritmo findEdgeCut() sólo iba a considerar las aristas no dirigidas "u-v" en modo compacto que son de la forma u≤v.
El siguiente paso es encontrar todos los caminos entre cada dos nodos con let path = findPath({matrix, firstIndex, lastIndex}). Si no hay camino guada esos nodos en result.stEmpty. Si hay camino aplica findSTEdgeCut({matrix, firstIndex, lastIndex}) para encontrar el corte mínimo entre esos nodos. Vamos almacenando temporalmente las aristas convertidas en texto en el conjunto sets, que es una instancia del constructor Set de JavaScript, así que que sólo se guardará un ejemplar de cada valor. Por otro lado guardamos en sts también la pareja "s" y "t" que aquí son firstIndex y lastIndex.
Cuando finalizamos iterando por todas las parejas de nodos convertimos el conjunto sets en un Array de JavaScript. Si el modo valor de la matriz de adyacencia del grafo es "0/number" significa que el grafo es ponderado, con lo que procedemos a ordenar la lista de resultados sets en orden creciente de la suma de sus pesos. En otro caso las ordenamos por el número de aristas, que es equivalente a considerar cada arista con peso unitario y sumar, pero es más simple hacerlo así.
Si la opción minimumSizeCut esta activada devolvemos en result.edges el primer resultado en sets, en otro caso los devolvemos todos. Finalmente sólo nos falta devolver result.st con la lista de parejas "s,t" que se corresponden en el mismo orden con las aristas de corte en result.edges.

En el resultado también se devuelve "warnings" que son avisos para aquellos grafos grandes donde no puede finalizar la ejecución con un número de iteraciones predeterminado. Como vemos en la Figura, una opción para todos los algoritmos es máximas iteraciones con un valor inicial de 10000. Se incluye un control de iteraciones en algunos algoritmos para evitar que la ejecución colapse el navegador.
En la Figura vemos un grafo con 400 nodos tratando de encontrar los cortes mínimos de aristas con la opción mínimo tamaño de corte marcada y encontrando el corte [[0,6],[0,7],[0,80]], que son las 3 primeras de la lista de aristas del grafo, pero dado que el algoritmo no pudo finalizar no puede asegurarse que no hay otro corte de aristas con menor tamaño que este.
Encontrar corte aristas: {
"edges":[[[0,6],[0,7],[0,80]]],
"st":[[[0,1],[0,2],[0,3]]],
"stEmpty":[[0,5],[0,6],[0,7],
..., (+ 79790)
[397,398],[397,399],[398,399]],
"warnings":["(findSTEdgeCut) Maximum iterations 10000 reached testing s=0 t=4"]}El control de iteraciones se superó cuando estaba chequeando la pareja de aristas "0,4" mediante findSTEdgeCut(), habiendo pasado ya por las parejas "0,1", "0,2" y "0,3". Al llegar a la pareja "0,4" se completan las 10000 iteraciones, que al ser una variable global también afecta al algoritmo findPath(), que aunque sigue revisando parejas hasta completarlas todas (400×400÷2 = 80000), el resto devuelve erróneamente que no hay camino entre ellas. En resumen, en caso de avisos de error no puede asegurarse la corrección del resultado.
Hay que notar que este algoritmo llama a findSTEdgeCut() que a su vez llama a findMaximumFlow(), usando repetidas veces findPath(), con lo que esto consume muchas iteraciones cuando el grafo tiene muchos nodos o aristas. Y aunque usando la opción método para flujo con valor "dijkstra" puede ayudar algo, aún así seguramente habrá una forma de hacerlo más eficiente, o incluso con otros enfoques para resolver el problema que el algoritmo plantea.
Puede abrir cfi-400-nodes.txt con la lista de aristas de ese grafo en formato de texto que puede copiar e importar en la aplicación tal como explicamos en un tema anterior sobre como importar una lista de aristas.
Comparar conjunto separador de aristas y corte de aristas

En la Figura vemos todos lo cortes mínimos de aristas para un grafo no dirigido, algo que ya expusimos más arriba en la Figura.
Encontrar corte aristas: {
"edges":[[[0,1],[0,4]],
[[1,2],[4,5]],
[[2,3],[3,5]],
[[0,1],[1,2],[1,4]],
[[1,2],[2,3],[2,5]]],
"st":[[[0,1],[0,2],[0,3],[0,4],[0,5]],
[[1,2],[1,3],[1,5],[2,4],[4,5]],
[[2,3],[3,4],[3,5]],
[[1,4]],
[[2,5]]],
"stEmpty":[],
"warnings":[]}| s-t | edges cut |
|---|---|
| [0,1],[0,2],[0,3],[0,4],[0,5] | [[0,1],[0,4]] |
| [1,2],[1,3],[1,5],[2,4],[4,5] | [[1,2],[4,5]] |
| [2,3],[3,4],[3,5] | [[2,3],[3,5]] |
| [1,4] | [[0,1],[1,2],[1,4]] |
| [2,5] | [[1,2],[2,3],[2,5]] |
Esos cortes agrupados por nodos "s" y "t" se vierten en esta tabla. Esto quiere decir que hay una relación entre corte mínimo de aristas y nodos "s" y "t" que se separan en componentes conectados distintos.
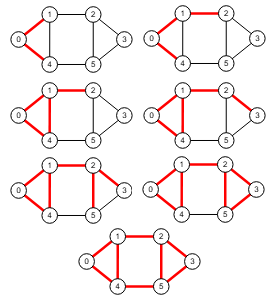
Mientras que los conjuntos separadores de aristas para ese grafo son desde 2 (pues no hay de tamaño 1) hasta 8 que es el total de aristas. En la Figura presentamos un ejemplar de cada tamaño y en la tabla siguiente se presentan cuántos hay de cada uno así como una muestra de los iniciales.
Un corte mínimo de aristas está incluido en algún conjunto separador de aristas.
| Tamaño | Separadores | |
|---|---|---|
| 1 | 0 | - |
| 2 | 3 | [[0,1],[0,4]], [[1,2],[4,5]], [[2,3],[3,5]] |
| 3 | 26 | [[0,1],[0,4],[1,2]], [[0,1],[0,4],[1,4]], ... |
| 4 | 70 | [[0,1],[0,4],[1,2],[1,4]], ... |
| 5 | 56 | [[0,1],[0,4],[1,2],[1,4],[2,3]], ... |
| 6 | 28 | [[0,1],[0,4],[1,2],[1,4],[2,3],[2,5]], ... |
| 7 | 8 | [[0,1],[0,4],[1,2],[1,4],[2,3],[2,5],[3,5]], ... |
| 8 | 1 | [[0,1],[0,4],[1,2],[1,4],[2,3],[2,5],[3,5],[4,5]] |
Obtener conectividad aristas getEdgeConnectivity()
La conectividad de aristas s-t de un grafo es el mínimo número de aristas que al eliminarlas separa los nodos "s" y "t" en distintos componentes conectados. Recordemos que al inicio del tema definimos que un corte mínimo de aristas s-t supone encontrar un conjunto mínimo de aristas que separe los nodos "s" y "t" en distintos componentes conectados, por lo que la conectividad es simplemente ese número mínimo de aristas.
El teorema de Menger para la conectividad de aristas dice que para dos vértices distintos "s" y "t" el número máximo de caminos independientes es igual que el mínimo número de aristas que es necesario eliminar para separar esos vértices "s" y "t" en componentes distintos. Y el teorema del máximo flujo y mínimo corte establece que la máxima cantidad de flujo que va de la fuente "s" al sumidero "t" es igual que el mínimo corte necesario para desconectar "s" y "t".
máximo flujo ≡
caminos independientes ≡
corte mínimo aristas
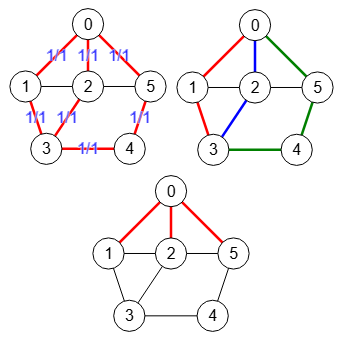
Así que la conectividad aristas equivale a el máximo flujo, o al número de caminos con aristas independientes o al número de corte mínimo de aristas entre nodos "s" y "t". En la Figura vemos estos tres grafos para "s=0" y "t=3".
Obtener conectividad aristas:
{"value":3,"warnings":[]}En la aplicación obtenemos el valor 3 para la conectividad de aristas con este algoritmo que vemos ahora getEdgeConnectivity().
Encontrar máximo flujo: {
"flow":3,
"residualMatrix":
[[0,0,0,0,0,0],
[2,0,1,0,0,0],
[2,1,0,0,0,1],
[0,2,2,0,2,0],
[0,0,0,0,0,2],
[2,0,1,0,0,0]],
"flowMatrix":
[[0,1,1,0,0,1],
[0,0,0,1,0,0],
[0,0,0,1,0,0],
[0,0,0,0,0,0],
[0,0,0,1,0,0],
[0,0,0,0,1,0]],
"edgesFlow":
{"0,1":1,"0,2":1,"0,5":1,
"1,3":1,"2,3":1,"4,3":1,
"5,4":1}}Y el mismo valor 3 para el máximo flujo con el algoritmo findMaximumFlow() que vimos en un tema anterior.
Encontrar caminos aristas independientes con máximo flujo: [[[0,1,3],[0,2,3],[0,5,4,3]]]
Y el mismo número de 3 caminos con aristas independientes usando máximo flujo con el algoritmo findEdgeIndependentPathsMaxFlow() que vimos en un tema anterior.
Encontrar corte aristas s-t: [[0,1],[0,2],[0,5]]
Y el mismo número 3 de corte mínimo de aristas s-t usando el algoritmo que vimos más arriba findSTEdgeCut().
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1},{"index":2},{"index":4}]},
{"index":4,"parent":[{"index":5}]},
{"index":5,"parent":[{"index":0},{"index":2}]}
],
"config":{
"algorithm":"Get edge connectivity",
"lastIndex":3,
"modeST":true
}}
Para Wolfram con EdgeConnectivity[g, 1, 4] devolverá también 3.
g = AdjacencyGraph[{{0,1,1,0,0,1},{1,0,1,1,0,0},{1,1,0,1,0,1},{0,1,1,0,1,0},{0,0,0,1,0,1},{1,0,1,0,1,0}},
ImageSize->188, VertexSize->{"Scaled", 0.17}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center]},
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White,
EdgeStyle->{{Black,Thickness[0.005]}}]
EdgeConnectivity[g, 1, 4]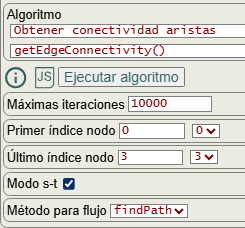
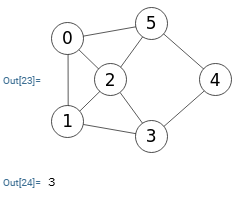
Entre las opciones para ejecutar getEdgeConnectivity() vemos modo s-t marcado, devolviendo la conectividad de aristas entre nodos "s" y "t" que son los nodos identificados con primer índice nodo y último índice nodo. Si no se marca modo s-t se devolverá la conectividad de aristas del grafo como veremos a continuación, ignorándose "s" y "t". Con método para flujo se indica "findPath", "dijkstra" o "floyd" como métodos para encontrar un camino cuando se ejecute findMaximumFlow() bien desde findSTEdgeCut() o desde findEdgeCut().
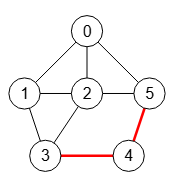
La conectividad de aristas de un grafo es el mínimo de todos los cortes mínimos de aristas para todas las parejas de nodos del grafo. Esto en base a la teoría que dice que la conectividad de aristas del grafo λ(G) es el mínimo de la conectividad de aristas s-t λ(s, t) sobre todas las parejas de distintos vértices "s" y "t" adyacentes o no.
Encontrar corte aristas: {
"edges":[[[3,4],[4,5]]],
"st":[[[0,4],[1,4],[2,4],[3,4],[4,5]]],"
stEmpty":[],
"warnings":[]}Para el grafo de la Figura encontramos que el corte mínimo de aristas del grafo son las dos aristas "3-4, 4-5", que vemos que no tiene porque coincidir con el corte mínimo de aristas entre nodos "s=0" y "t=3" que vimos antes. Esa ejecucion se corresponde con el algoritmo findEdgeCut().
Obtener conectividad
aristas: {
"value":2,
"warnings":[]}Ejecutando getEdgeConnectivity() obtenemos el valor 2, pues es el mínimo número de aristas que son necesarias para separar el grafo.
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1},{"index":2},{"index":4}]},
{"index":4,"parent":[{"index":5}]},
{"index":5,"parent":[{"index":0},{"index":2}]}
],
"config":{
"algorithm":"Get edge connectivity"
}}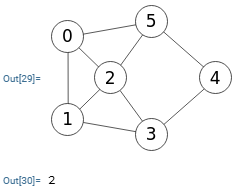
En la Figura vemos que Wolfram también devuelve 2 usando EdgeConnectivity[g] sin argumentos de nodos "s-t".
g = AdjacencyGraph[{{0,1,1,0,0,1},{1,0,1,1,0,0},{1,1,0,1,0,1},{0,1,1,0,1,0},{0,0,0,1,0,1},{1,0,1,0,1,0}},
ImageSize->188, VertexSize->{"Scaled", 0.17}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center]},
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White,
EdgeStyle->{{Black,Thickness[0.005]}}]
EdgeConnectivity[g]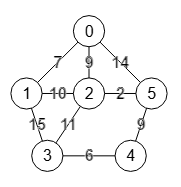
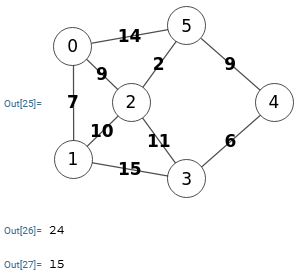
Para un grafo ponderado como el de la Figura vemos los siguientes resultados para la conectividad de aristas s-t entre nodos "0" y "3" así como la conectividad general del grafo:
Con modo s=0 t=3
Obtener conectividad aristas:
{"value":24,"warnings":[]}
Sin modo s-t
Obtener conectividad aristas:
{"value":15,"warnings":[]}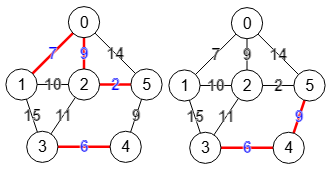
Para entender esos resultados vemos en el de la izquierda de la Figura el corte mínimo de aristas entre nodos "0" y "3", cuya suma de pesos 7+9+2+6=24 de las aristas "0-1, 0-2, 2-5, 3-4" es el valor 24 que hemos obtenido para la conectividad de aristas en modo s-t. Para el mismo grafo no ponderado veíamos en el último grafo de la Figura que el corte mínimo entre "0" y "3" eran las aristas "0-1, 0-2, 0-3" con lo que la conectividad tiene valor 3, pues en grafos no ponderamos la conectividad coincide con el número de aristas pues se considera cada arista con peso unitario.
En el de la derecha de la Figura vemos el corte mínimo de aristas "3-4, 4-5" del grafo, cuya suma de pesos 6+9=15 coincide con el valor 15 que obtuvimos para la conectivididad de aristas del grafo.
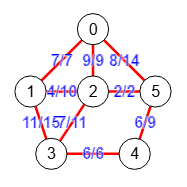
Si ejecutamos el algoritmo findMaximumFlow() para encontrar el máximo flujo entre nodos "0" y "3" obtenemos el grafo de la Figura, con el resultado "flow":24 con el mismo valor que la conectividad s-t que obtuvimos antes, observando que es la suma de las capacidades usadas en las 3 aristas salientes del nodo fuente "s" (7+9+8=24) o, también, las 3 entrantes en el nodo sumidero "t" (11+7+6=24). Recuerde que para las etiquetas "a/b" de las aristas en estos grafos de flujo, "a" es la capacidad usada y "b" es la capacidad total de la arista, de tal forma que la capacidad total usada saliente del nodo "s" ha de ser igual que la entrante al nodo "t", siendo por tanto también el máximo flujo.
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0,"value":7}]},
{"index":2,"parent":[{"index":0,"value":9},{"index":1,"value":10}]},
{"index":3,"parent":[{"index":1,"value":15},{"index":2,"value":11},{"index":4,"value":6}]},
{"index":4,"parent":[{"index":5,"value":9}]},
{"index":5,"parent":[{"index":0,"value":14},{"index":2,"value":2}]}
],
"config":{
"algorithm":"Get edge connectivity",
"lastIndex":3,
"modeST":true
}}
En Wolfram obtenemos los mismos valores 24 y 15 para la conectividad aristas para "s=0" y "t=3" y para el grafo respectivamente.
g = WeightedAdjacencyGraph[{{∞,7,9,∞,∞,14},{7,∞,10,15,∞,∞},{9,10,∞,11,∞,2},{∞,15,11,∞,6,∞},{∞,∞,∞,6,∞,9},{14,∞,2,∞,9,∞}},
ImageSize->188, VertexSize->{"Scaled", 0.17}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center]}, VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], EdgeLabels->{(2->1)->7, (3->1)->9, (3->2)->10, (4->2)->15, (4->3)->11, (4->5)->6,
(5->6)->9, (6->1)->14, (6->3)->2}, VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}]
EdgeConnectivity[g, 1, 4]
EdgeConnectivity[g]El código JavaScript para ejecutar getEdgeConnectivity() usa findSTEdgeCut o findEdgeCut según el argumento modeST que ya explicamos que se pasaba como la opción modo s-t al algoritmo. Con getMatrixModeValue() obtenemos el modo valores de la matriz, pues lo vamos a necesitar para cuando tengamos un grafo ponderado, lo que se detecta con el modo valor "0/number", sumándose entonces los pesos de las aristas de corte. Y en otro caso simplemente devolvemos el número de aristas de corte pues se consideran pesos unitarios y la suma coincide con el número de aristas.
function getEdgeConnectivity({matrix=[], firstIndex=0, lastIndex=0, modeST=false, methodFlow="findPath"}) {
let result = {value: 0, warnings: []}, temp;
try {
temp = getMatrixModeValue({matrix});
if (typeof temp==="string") throw new Error (temp);
let [modeValue, nullValue] = temp;
if (modeST) {
temp = findSTEdgeCut({matrix, firstIndex, lastIndex, methodFlow});
} else {
temp = findEdgeCut({matrix, minimumSizeCut:true, methodFlow});
}
if (typeof temp==="string") throw new Error(temp);
let edges = modeST ? temp : temp.edges[0];
result.warnings = modeST ? [] : temp.warnings;
if (edges.length>0){
if (modeValue==="0/number") {
result.value = edges.reduce((p,v) => (p+=matrix[v[0]][v[1]], p), 0);
} else {
result.value = edges.length;
}
}
} catch(e){result = e.message}
return result;
}