19 feb 2021

Algoritmos CRC básicos

La función mod(x, y, z)

Generar el CRC es en esencia calcular el resto de la división entre un mensaje (el dividendo) y un polinomio (el divisor). Veíamos en el tema anterior que en lugar de utilizar el algoritmo de la división usábamos el algoritmo del resto, que es el mismo pero enfocándonos en obtener el resto más que el cociente:

function mod(x="0", y="0", r="0") {
    r = r.padStart(y.length, "0");
    for (let k=0; k<x.length; k++) {
        r = xor(shiftLeft(r, 1), x[k]).padStart(y.length, "0");
        if (r[0]==="1") {
            r = xor(r, y).padStart(y.length, "0");
        }
    }
    return r;
}

En el último apartado del tema anterior resolvíamos con un algoritmo básico crcBytesBasic() el resto de un dividendo que podría ser muy largo, como todos los bytes de un archivo, tomando en cada paso un único byte y arrastrando el resto anterior en el tercer argumento del algoritmo del resto en módulo 2 o resto Mod2.

Para realizar mejoras al algoritmo básico hemos de aplicar un poco de matemáticas. Empezaremos traduciendo este algoritmo del resto Mod2 en una función matemática que expresaremos como mod(x, y, z). En matemáticas con números decimales la función mod(x, y) es la aplicación del operador módulo x mod y. Si decimos que r = mod(x, y) es debido a que existe un c tal que x = y × c + r. Veamos ahora que es mod(x, y, z).

Definimos mod(x, y, z) = mod(x + z·10^d, y) siendo d el número de dígitos de x. Por ejemplo, mod(58927, 321) = 184. Y también mod(8927 + 5·10⁴, 321) = 184. Y por la definición con el tercer argumento mod(8927, 321, 5) = 184 también. Esto quiere decir que podemos traspasar dígitos por la izquierda del dividendo y trasladarlos al tercer argumento z. Y viceversa.

Vease que cuando z=0 entonces mod(x, y, 0) = mod(x, y).

Si definimos 0_d = 0·10^d-1 + 0·10^d-2 + ... + 0·10¹ + 0·10⁰ como una cadena con d ceros, entonces si x tiene d dígitos podemos traspasar del primer al tercer argumento con mod(x, y z) = mod(0_d, y, x 10^-d + z), pues si volvemos a traspasar x al primer argumento hemos de saber cuántos dígitos tiene ese primer argumento cero. Así que 0_d matemáticamente equivale a cero, pero mantiene información de los dígitos importante a la hora de manejar el traspaso de argumentos. Vease que 0₀ = ∅, es decir, un cero repetido cero dígitos es realmente un conjunto vacío de dígitos.

Para calcular manualmente mod(58927, 321) en aritmética normal en base diez haríamos una simple división entera y obtendríamos el resto 184:

 58927  │ 321
        └──────
-321      183
─────
 2682
-2568
 ─────
  1147
  -963
  ────
   184

Operar mod(58927, 321) = mod(58927, 321, 0), donde usamos el tercer argumento con un cero, lo podríamos hacer manualmente con un algoritmo del resto en lugar de usar el de la división. El tercer argumento inicia el registro resaltado en amarillo, registro que tendrá un dígito más que el divisor. El resto será un valor entre 0 y 320, una unidad menos que el divisor. Por lo tanto el registro tendrá 4 dígitos. A la derecha está el dividendo. En cada paso vamos trasladando dígitos desde la izquierda del dividendo a la derecha del registro. Cuando exista un dígito 1 a 9 que multiplicado por el divisor sea menor o igual que el registro, realizamos la resta. Continuamos así hasta agotar todos los dígitos del dividendo.

58927 MOD 321 ⇒
     0000    58927
k=0  0005    8927
k=1  0058    927
k=2  0589    27
     0589-1×321=589-321=268
k=3  2682    7
     2682-8×321=2682-2568=114
k=4  1147
     1147-3×321=1147-963=184

En el fondo es el mismo algoritmo que el de la división, pero puesto de otra forma. Observe los dígitos del cociente resaltados en azul.

Con la función mod(x, y, z) tras trasladar un dígito al tercer argumento, operamos mod(8927, 321, 5) donde el registro se inicia con 0005:

8927 MOD 321 ⇒
     0005    8927
k=0  0058    927
k=1  0589    27
     0589-1×321=589-321=268
k=2  2682    7
     2682-8×321=2682-2568=114
k=3  1147
     1147-3×321=1147-963=184

En binario y con aritmética Mod2 vimos en el tema anterior mod(000, 1011, 101):

000 MOD 1011 ⇒ 
     0101    000
k=0  1010    00
     1010 XOR 1011 = 0001
k=1  0010    0
k=2  0100

Observe que es el mismo algoritmo con registro que el expuesto en base decimal, sólo que:

El registro tiene los mismos dígitos que el divisor pues no hay acarreos
La resta se sustituye por un XOR
Aplicamos XOR cuando el primer dígito del registro sea uno
No necesitamos buscar un dígito 1 a 9 para multiplicar por el divisor pues siempre será 1

Esto supone tal facilidad de implementación que es por lo que se utiliza para el cálculo del CRC.

Extrayendo argumentos al exterior de mod(x, y, z)

Podemos extraer el primer argumento al exterior con lo siguiente:

r = mod(x, y, z) = mod(mod(0_d, y, z) + x, y)

Para demostrarlo partiremos de la expresión final y llegaremos a la inicial:

r = mod(mod(0_d, y, z) + x, y) ⇒ Existe b tal que ⇒ mod(0_d, y, z) + x = y·b + r ⇒ Aplicando mod(x, y, z) = mod(x + z 10^d, y) mod(z 10^d, y) + x = y·b + r ⇒ mod(z 10^d, y) = y·b + r - x ⇒ Existe a tal que ⇒ z 10^d = y·a + y·b + r - x ⇒ Haciendo c = a + b z 10^d = y·c + r - x ⇒ x + z 10^d = y·c + r ⇒ r = mod(x + z 10^d, y) ⇒ r = mod(x, y, z)

La demostración es simple cuando z=0 puesto que mod(mod(0_d, y, 0) + x, y) = mod(mod(0, y) + x, y) = mod(0 + x, y) = mod(x, y) dado que mod(0, y) = 0.

Aunque hemos extraido x desde el primer argumento al exterior del mod, también es posible extraer parte del argumento. Si x tiene d dígitos siendo de la forma x = x₀ 10^d-1 + x₂ 10^d-2 + ... + x_d-1 10 + x entonces si nombramos X_d-1 = x₂ 10^d-2 + ... + x_d-1 10 + x la parte derecha quitando el primer dígito, parte que tiene d-1 dígitos:

r = mod(x₀ 10^d-1 + X_d-1, y) = mod(mod(x₀ 10^d-1, y) + X_d-1, y)

Por ejemplo, con r = mod(58927, 321) = 58927 mod 321= 184, entonces 58927 = 5·10⁴ + 8927, extraemos los cuatro últimos dígitos mod(mod(5·10⁴, 321) + 8927, 321). Comprobemos esto calculando por partes:

mod(50000, 321) = 245 245 + 8927 = 9172 mod(9172, 321) = 184

Vease que la suma con el primer resto produce un resto mayor de 321 y es por lo que aplicamos nuevamente mod.

O bien 58927 = 58·10³ + 927, extraemos los dos primeros mod(mod(927, 321) + 58·10³, 321). Comprobemos esto calculando por partes:

mod(927, 321) = 285 285 + 58000 = 58285 mod(58285, 321) = 184

También puede extraerse desde el tercer argumento, pues z se hubo trasladado previamente desde el primer argumento:

r = mod(x, y, z) = mod(x + z 10^d, y) = mod(mod(x, y) + z 10^d, y)

Cuando operemos con aritmética Mod2 donde no hay acarreos, la suma se sustituye por un XOR. Si sumamos XOR dos números, el resultado no tendrá más dígitos que el que tenga más longitud. Así que no es necesario aplicar el mod externo en las expresiones anteriores.

Las expresiones que hemos visto en este apartado se aplican en Mod2 tal como sigue, donde ^ es la operación XOR:

r = mod(x, y, z) = mod(0_d, y, z) ^ x r = mod(x₀ 10^d-1 + X_d-1, y) = mod(x₀ 10^d-1, y) ^ X_d-1 r = mod(x, y, z) = mod(x, y) ^ z 10^d

Lo expuesto en estos dos primeros apartados nos será útil cuando mejoremos los algoritmos de cálculo del CRC en los apartados siguientes.

El algoritmo CRC bytes básico

Veamos como podemos aplicar mod(x, y, z) para calcular el resto. Empecemos por fijar algunas definiciones.

Supongamos que r = mod(x, y). Podemos expresar el dividendo x como un polinomio con coeficientes x_i y potencias bⁱ, donde b es la base numérica, con términos que son de la forma x_i bⁱ:

x = x_n bⁿ + x_n-1 b^n-1 + ... + x_i bⁱ + ... + + x₂ b² + x₁ b+ x₀

Por ejemplo, con base decimal

58927 = 5·10⁴ + 8·10³ + 9·10² + 2·10¹ + 7·10⁰

A efectos de simplificar los desarrollos en estos temas usaremos una base 10, no perdiendo de vista que la implementación del algoritmo se realizará en base 2, es decir, en binario. Como 10 en binario es 2 en decimal, cuando apliquemos estas expresiones en algoritmos binarios entenderemos que 10 es realmente el binario 0b10. Cambiaremos también el orden de los coeficientes, es decir, cada término será de la forma x_i 10^n-i:

x = x₀ 10ⁿ + x₁ 10^n-1 + ... + x_i 10^n-i + ... + x_n-2 10² + x_n-1 10 + x_n

Podemos definir un segmento de la entrada como x_{[i, d]} = mid(x, i·d, d), donde la función mid(x, i, d) actuaría sobre una cadena x de caracteres, tomando d de ellos empezando en la posición i. En JavaScript existe el método substr() que hace lo mismo que mid(). En sentido general hablaremos de x_{[i, d]} como un byte. Si x fueran los k bytes de un archivo, entonces cada byte tiene d = 8 bits y por tanto x tiene n = k·8 bits. Así que con x_{[i, 8]} = mid(x, i·8, 8) iterando desde i = 0 obtendríamos los bytes de ese archivo.

Cuando n es un múltiplo de d bits entonces i ∈ {0, 1, 2, 3, ..., k-1} con k = n / d bytes, como el caso de los bytes de un archivo. Si n no es múltiplo de d entonces k = ⌈ n/d ⌉. Pero en ese caso el último byte tendría una longitud inferior a d. Se podría arreglar agregando ceros al inicio de x con objeto de que sea un múltiplo, pues los ceros a la izquierda del dividendo no modifican la división ni la obtención del resto.

Si d = 1 entonces x_{[i, 1]} = x_i que coincidirá con un único coeficiente en x.

Matemáticamente podemos definir el segmento o byte de la entrada como sigue:

x_{[i, d]} = ⌊ (x - ⌊ x ÷ 10^n-i·d ⌋ 10^n-i·d) ÷ 10^n-(i+1)d ⌋

Hagamos un ejemplo con x = 158927 para obtener los segmentos 15, 89, 27 de longitud d=2:

x = 158927 n = 6 d = 2 i = 0 ⇒ x_{[0, 2]} = ⌊ (158927 - ⌊ 158927 ÷ 10⁶ ⌋ 10⁶) ÷ 10⁴ ⌋ = ⌊ (158927 - 0) ÷ 10⁴ ⌋ = ⌊ 158927 ÷ 10⁴ ⌋ = 15 i = 1 ⇒ x_{[1, 2]} = ⌊ (158927 - ⌊ 158927 ÷ 10⁴ ⌋ 10⁴) ÷ 10² ⌋ = ⌊ (158927 - 150000) ÷ 10² ⌋ = ⌊ 8927 ÷ 10² ⌋ = 89 i = 2 ⇒ x_{[2, 2]} = ⌊ (158927 - ⌊ 158927 ÷ 10² ⌋ 10²) ÷ 10⁰ ⌋ = ⌊ (158927 - 158900) ÷ 10⁰ ⌋ = ⌊ 27 ÷ 10⁰ ⌋ = 27

La definición matemática del segmento o byte realmente no es necesaria implementarla, pues la extracción de bytes nos vendrá dada en el algoritmo. Pero es importante entender su aspecto matemático pues el objetivo es calcular r = mod(x, y) de una forma recurrente usando un byte x_{[i, d]} en cada paso.

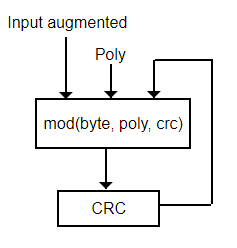
*Figura*. Esquema algoritmo CRC bytes básico

En el último apartado del tema anterior presentamos el algoritmo básico para obtener el CRC a partir de los bytes de un archivo. Volvemos a repetir el esquema en la Figura, pues representa la siguiente recurrencia:

r_i = mod ( x_{[i, d]}, y, r_i-1 )

Cada resto parcial r_i es el CRC calculado en cada paso de la iteración, valor que al final de los bucles será el CRC calculado. Se ejecuta un primer bucle con los bytes del archivo y un segundo bucle con tantos bytes cero como el ancho del polinomio. En cada iteración tomamos un byte x_{[i, d]}, con d = 8 bits.

Volvemos a presentar el algoritmo básico del tema anterior para comprobar como implementamos la recurrencia anterior. Vease que x nos viene en el argumento arrayBytes, el polinomio poly viene sin el (1) inicial, por lo que agregamos ceros al inicio hasta completar el ancho width y anteponemos un 1. Se ejecutan un primer bucle con la entrada sin aumentar y otro con el aumento de entrada. En ambos casos se ejecuta mod(byte, poly, crc) que equivale a la recurrencia anterior.

function crcBytesBasic({arrayBytes=[], width=0, poly="0"}){
    poly = "1" + hexToBin(poly).padStart(width, "0");
    let widthBytes = Math.ceil(width/8);
    let widthLastByte = width-8*(widthBytes-1);
    let crc = "0".repeat(width);
    for (let i=0; i<arrayBytes.length; i++){
        let Byte = arrayBytes[i].toString(2).padStart(8, "0");
        crc = mod(Byte, poly, crc);
    }
    for (let i=0; i<widthBytes; i++) {
        let Byte = "0".repeat(i===widthBytes-1 ? widthLastByte : 8);
        crc = mod(Byte, poly, crc);
    }
    return crc;
}

Volvamos a la recurrencia, que debe tener un caso base para poder resolverla, iniciándose con un valor cero:

i=-1 ⇒ r_i = 0 i≥0 ⇒ r_i = mod(x_{[i, d]}, y, r_i-1)

Para demostrar que esto obtiene el resto esperado, usaremos bytes de un único dígito x_{[i, 1]} = x_i que facilita las expresiones, obteniéndose los restos parciales siguientes usando la recurrencia r_i = mod(x_i, y, r_i-1):

r_-1 = 0 r₀ = mod(x₀, y, 0) r₁ = mod(x₁, y, r₀) r₂ = mod(x₂, y, r₁) ... r_n-1 = mod(x_n-1, y, r_n-2) r_n = mod(x_n, y, r_n-1)

Se puede demostrar que r = r_n, es decir, mod(x, y) = mod(x_n, y, r_n-1). En el siguiente desplegable puede consultar esa demostración que, repetimos, es para x_{[i, 1]} = x_i, pero que también se podría aplicar a segmentos o bytes de mayor tamaño.

Demostrar que mod(x, y) = mod(x_n, y, r_n-1)

Recordando como es el dividendo x:

x = x₀ 10ⁿ + x₁ 10^n-1 + ... + x_i 10^n-i + ... + x_n-2 10² + x_n-1 10 + x_n

Vamos a desplegar esa recurrencia para obtener el resultado final. Vease que aplicando la definición mod(x, y, z) = mod(x + z·10^d, y) siendo d=1 el número de dígitos de x_i, es decir, cada x_{[i, 1]} = x_i representa un único dígito

r_i = mod(x_i, y, r_i-1) = mod(x_i + r_i-1 10¹, y) ⇒ x_i + r_i-1 10 = y c_i + r_i

De donde podemos expresar la recurrencia como sigue:

i=-1 ⇒ r_i = 0 i≥0 ⇒ r_i = x_i + r_i-1 10 - y c_i

Desplegamos desde i=n hasta i=0:

i=n ⇒ r_n = x_n + r_n-1 10 - y c_n

i=n-1 ⇒ r_n = x_n + (x_n-1 + r_n-2 10 - y c_n-1) 10 - y c_n = x_n + x_n-1 10 + r_n-2 10² - y (c_n + c_n-1 10)

i=n-2 ⇒ r_n = x_n + x_n-1 10 + x_n-2 10² + r_n-3 10³ - y (c_n + c_n-1 10 + c_n-2 10²)

...

i=j ⇒ r_n = x_n + x_n-1 10 + ... + x_j 10^n-j + r_j-1 10^n-j+1 - y (c_n + c_n-1 10 + ... + c_j 10^n-j)

...

i=2 ⇒ r_n = x_n + x_n-1 10 + ... + x₂ 10^n-2 + r₁ 10^n-1 - y (c_n + c_n-1 10 + ... + c₂ 10^n-2)

i=1 ⇒ r_n = x_n + x_n-1 10 + ... + x₁ 10^n-1 + r₀ 10ⁿ - y (c_n + c_n-1 10 + ... + c₁ 10^n-1)

i=0 ⇒ r_n = x_n + x_n-1 10 + ... + x₀ 10ⁿ + r_-1 10ⁿ⁺¹ - y (c_n + c_n-1 10 + ... + c₀ 10ⁿ)

Como r_-1 = 0 entonces podemos resolver la recurrencia:

r_n = x_n + x_n-1 10 + ... + x₀ 10ⁿ - y (c_n + c_n-1 10 + ... + c₀ 10ⁿ) ⇒ r_n = mod(x, y)

puesto que el dividendo es x = x_n + x_n-1 10 + ... + x₀ 10ⁿ y el cociente es c = c_n + c_n-1 10 + ... + c₀ 10ⁿ.

Resolvamos la operación con base númerica decimal mod(58927, 321) = 184 usando la recurrencia anterior, recordando que para resolver mod(x, y, z) debemos aplicar el cálculo de mod(x + z 10^d, y) siendo d el número de dígitos de x. Con este ejemplo d=1 pues tomaremos bytes de 1 dígito:

x = 58927 y = 321 d = 1 r_-1 = 0 r₀ = mod(x_{[0, 1]}, y, r_-1) = mod(5, 321, 0) = mod(5+0·10, 321) = 5 mod 321 = 5 r₁ = mod(x_{[1, 1]}, y, r₀) = mod(8, 321, 5) = mod(8+5·10, 321) = 58 mod 321 = 58 r₂ = mod(x_{[2, 1]}, y, r₁) = mod(9, 321, 58) = mod(9+58·10, 321) = 589 mod 321 = 268 r₃ = mod(x_{[3, 1]}, y, r₂) = mod(2, 321, 268) = mod(2+268·10, 321) = 2682 mod 321 = 114 r₄ = mod(x_{[4, 1]}, y, r₃) = mod(7, 321, 114) = mod(7+114·10, 321) = 1147 mod 321 = 184

Realicemos el mismo ejemplo tomando ahora bytes con d = 2 dígitos. Agregaremos un 0 delante del dividendo x con objeto de que su número de dígitos sea un múltiplo de d = 2:

x = 058927 y = 321 d = 2 r_-1 = 0 r₀ = mod(x_{[0, 2]}, y, r_-1) = mod(05, 321, 0) = mod(05+0·10², 321) = 5 mod 321 = 5 r₁ = mod(x_{[1, 2]}, y, r₀) = mod(89, 321, 5) = mod(89+5·10², 321) = 589 mod 321 = 268 r₂ = mod(x_{[2, 2]}, y, r₁) = mod(27, 321, 268) = mod(27+268·10², 321) = 26827 mod 321 = 184

Hagamos ahora el ejemplo del apartado anterior con la entrada en binario x = 01111010, un único byte (d=8) que se corresponde con la letra "z" en ASCII. El polinomio era (1)011 con un ancho de w=3 bits. Por lo tanto el aumento de entrada serán tres ceros a = 000. En este caso resolvemos los mod(x, y, z) directamente usando la calculadora de Web Tools online.

x = 01111010 y = 1011 d = 8 w = 3 a = 000 INICIO: r_-1 = 0 PRIMER BUCLE r₀ = mod(x_{[0, 8]}, y, r_-1) = mod(01111010, 1011, 0) = 101 crc = 101 SEGUNDO BUCLE r₀ = mod(x_{[0, 3]}, y, crc) = mod(000, 1011, 101) = 100 crc = 100

Hemos obtenido el mismo CRC 100 esperado. Observe como se obtienen los mismos restos parciales, 101 en el primer bucle, valor que inicia el segundo obteniéndose el 100 final, lo mismo que si hacemos el cálculo de 01111010000 mod 1011 en aritmética Mod2:

1111010000 MOD 1011 ⇒ 
      0000    1111010000
k= 0  0001    111010000
k= 1  0011    11010000
k= 2  0111    1010000
k= 3  1111    010000
      1111 XOR 1011 = 0100
k= 4  1000    10000
      1000 XOR 1011 = 0011
k= 5  0111    0000
k= 6  1110    000
      1110 XOR 1011 = 0101
k= 7  1010    00
      1010 XOR 1011 = 0001
k= 8  0010    0
k= 9  0100

La siguiente traza del algoritmo crcBytesBasic() se obtiene de la herramienta que reproduce ese mismo ejemplo y que expusimos también en el tema anterior:

Input: z ⇒ arrayBytes = [01111010]
Width: 3
Poly: 0x3 ⇒  (1)011
bytes = arrayBytes.length = 1
widthBytes = Math.ceil(width/8) = 1
widthLastByte = width-8*(widthBytes-1) = 3
crc = 000
INPUT LOOP for i=0 to 0
i=0 ⇒ byte = arrayBytes[0] = 01111010
crc = mod(byte, poly, crc) = mod(01111010, 1011, 000) =
01111010 MOD 1011 ⇒ 
     0000    01111010
k=0  0000    1111010
k=1  0001    111010
k=2  0011    11010
k=3  0111    1010
k=4  1111    010
     1111 XOR 1011 = 0100
k=5  1000    10
     1000 XOR 1011 = 0011
k=6  0111    0
k=7  1110
     1110 XOR 1011 = 0101
INPUT AUGMENTED LOOP for j=0 to 0
j=0 ⇒ byte = "0".repeat(3) = 000
crc = mod(byte, poly, crc) = mod(000, 1011, 101) =
000 MOD 1011 ⇒
     0101    000
k=0  1010    00
     1010 XOR 1011 = 0001
k=1  0010    0
k=2  0100
crc = 100 ⇒ 0x4

Algoritmo CRC bytes básico 2: Evitando el segundo bucle

La primera mejora que vamos a acometer es evitarnos el segundo bucle del aumento de la entrada. Empecemos recordando como era el dividendo x:

x = x₀ 10ⁿ + x₁ 10^n-1 + ... + x_i 10^n-i + ... + x_n-2 10² + x_n-1 10 + x_n

La entrada aumentada x' con w ceros consiste en añadir tantos ceros a la derecha de la entrada x como el ancho width (w) del polinomio, lo que equivale a multiplicar x por 10^w:

x' = ( x₀ 10ⁿ + ... + x_i 10^n-i + ... + x_n ) 10^w = x₀ 10^n+w + ... + x_i 10^n-i+w + ... + x_n 10^w + 0·10^w-1 + 0·10^w-2 + ... + 0·10 + 0

Antes teníamos r_i = mod(x_{[i, d]}, y, r_i-1) para la entrada sin aumentar. Ahora hemos de obtener r'_i = mod(x'_{[i, d]}, y, r'_i-1) para la entrada x' aumentada.

Como x'_{[i, d]} = x_{[i, d]} 10^w entonces:

r'_i = mod(x'_{[i, d]}, y, r'_i-1) = mod(x_{[i, d]} 10^w, y, r'_i-1)

Recordando que si mod(x, y, z) = mod(x + z 10^d, y) entonces podemos pasar x al tecer argumento quedando mod(x, y, z) = mod(0_d, y, x 10^-d + z) siendo 0_d una cadena con d ceros, matemáticamente equivalente a cero:

r'_i = mod(x_{[i, d]} 10^w, y, r'_i-1) = mod(0_d, y, x_{[i, d]} 10^w-d + r'_i-1)

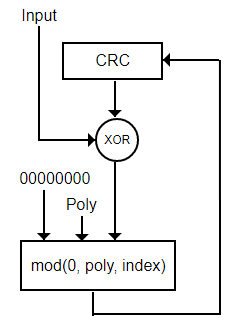
En definitiva nos queda la siguiente recurrencia general, donde la suma es un XOR y 10 es el número binario 0b10 (2 en decimal):

r'_i = mod ( 0_d, y, x_{[i, d]} 10^w-d + r'_i-1 )

Vease que los bytes x_{[i, d]} se obtienen de la entrada sin aumentar x. Como estamos obteniendo r'_i sobre la entrada aumentada, entonces supone que podemos omitir el segundo bucle del aumento de la entrada.

El esquema de la Figura representa la recurrencia anterior. Ahora se toma la entrada (Input) sin aumentar. La suma x_{[i, d]} 10^w-d + r'_i-1 de un byte con el resto anterior se aplica en aritmética Mod2 con un XOR. El resultado de esta suma lo denominamos index, puesto que en una mejora posterior adquirirá su significado.

Para la implementación del CRC sobre bytes de un archivo, el primer argumento del mod() será siempre una cadena con d = 8 ceros, es decir, 0₈ = 00000000. A continuación mostramos el algoritmo crcBytesBasic2() que implementa la recurrencia anterior.

function crcBytesBasic2({arrayBytes=[], width=0, poly="0"}){
    let widthBits = Math.max(width, 8);
    poly = "1" + hexToBin(poly).padStart(width, 0").padEnd(widthBits,"0");
    let crc =  "0".repeat(widthBits);
    for (let i=0; i<arrayBytes.length; i++){
        let Byte = arrayBytes[i].toString(2).padStart(8, "0");
        let bytePlus = Byte.padEnd(widthBits, "0");
        let index = xor(bytePlus, crc);
        crc = mod("00000000", poly, index);
    }
    crc = crc.substr(1, width);
    return crc;
}

Si width es menor de d=8 bits se ajusta a 8 bits, ajuste que se calcula con widthBits. Se trata de evitar el caso w<d en la recurrencia, pues entonces el término x_{[i, d]} 10^w-d tendrá una potencia negativa, complicando los cálculos en arimética Mod2.

Para evitarlo podemos multiplicar numerador y denominador de la división x÷y por la potencia 10^d-w, es decir, x ÷ y = (x 10^d-w) ÷ (y 10^d-w) y, de igual forma, del cálculo del resto r = x 10^d-w mod y 10^d-w. El resto tendrá d-w ceros a la derecha, ajustándolo finalmente con r = r ÷ 10^d-w. Por ejemplo, 58927 mod 321 = 184 mientras que 58927000 mod 321000 = 184000, con lo que ajustamos con 184000 ÷ 1000 = 184. Es por eso que cuando el ancho width del polinomio es menor de 8 bits, ajustamos el polinomio hasta 8 bits con widthBits = Math.max(width, 8) en el algoritmo.

Al final del cálculo del CRC hacemos el ajuste para quitar el exceso de ceros por la derecha. Este ajuste final puede llevarse a cabo recortando el CRC final (recordar que es un String) desde la posición 1 a width. Se recorta desde la posición 1 puesto que el resto que nos devuelve la función mod() tiene un byte inicial a cero correspondiente al XOR con el (1) inicial del polinomio que siempre resultará cero.

Para ver la base matemática de lo anterior observe la recurrencia anterior antes de traspasar de argumento:

r'_i = mod(x_{[i, d]} 10^w, y, r'_i-1)

Si w<d multiplicamos dividendo y divisor por 10^d-w, llegando a una recurrencia donde el divisor y está ajustado con d-w bits y el byte x_{[i, d]} aparece sin ninguna potencia:

r'_i =mod(x_{[i, d]} 10^w 10^d-w, y 10^d-w, r'_i-1) = mod(x_{[i, d]} 10^d, y 10^d-w, r'_i-1) = mod(0_d, y 10^d-w, x_{[i, d]} + r'_i-1)

Con Byte.padEnd(widthBits,"0"), donde widthBits es max(w, d), se lleva a cabo el cálculo de x_{[i, d]} 10^w-d que tendrá una longitud de w. Es lo mismo que agregar por la derecha w-d ceros. O bien agregar ceros con padEnd() para que tenga un ancho w.

Veamos una traza de un ejemplo que hemos visto en apartados anteriores.

Input: z ⇒ arrayBytes = [01111010]
Width: 3
Poly: 0x3 ⇒  (1)011
bytes = arrayBytes.length = 1
widthBits = Math.max(width, 8) = 8
poly 1011 adjusted with 5 zeros = 101100000
crc = 00000000

Se ajusta el polinomio con width = 3 que es menor que d = 8 bits agregando d-w = 8-3 = 5 ceros al final. Ese añadido se lo quitaremos al final. Vea que sólo hay un bucle con la entrada sin aumentar.

INPUT LOOP for i=0 to 0
i=0 ⇒ byte = arrayBytes[0] = 01111010
bytePlus = byte.padEnd(8, "0") = 01111010
index = xor(bytePlus, crc) = xor(01111010, 00000000) = 1111010
crc = mod(00000000, poly, index) = mod(00000000, 101100000, 1111010) =
00000000 MOD 101100000 ⇒ 
     001111010    00000000
k=0  011110100    0000000
k=1  111101000    000000
     111101000 XOR 101100000 = 010001000
k=2  100010000    00000
     100010000 XOR 101100000 = 001110000
k=3  011100000    0000
k=4  111000000    000
     111000000 XOR 101100000 = 010100000
k=5  101000000    00
     101000000 XOR 101100000 = 000100000
k=6  001000000    0
k=7  010000000
Adjust CRC = 10000000 to width=3 bits:  crc = 100 ⇒ 0x4

Algoritmo CRC con índice de un byte

En el algoritmo anterior obtuvimos la recurrencia r'_i = mod(0_d, y, x_{[i, d]} 10^w-d + r'_i-1) de la cual analizaremos el tercer argumento x_{[i, d]} 10^w-d + r'_i-1, operación que en el algoritmo declaramos con la variable index. Esta suma se implementa con un XOR en el algoritmo. Vemos que el byte x_{[i, d]} tiene una longitud de d dígitos. Y por tanto x_{[i, d]} 10^w-d tendrá una longitud de w dígitos. Por otro lado r'_i-1 es un resto parcial y por tanto tendrá también una longitud w. El XOR entre ambos, es decir, el valor de index = x_{[i, d]} 10^w-d + r'_i-1 tiene una longitud de w dígitos.

Con ese index ejecutábamos mod(0_d, y, index) en cada iteración. Vease que en esta expresión los dos primeros argumentos son constantes durante la ejecución para un d=8 bits, es decir, para calcular el CRC de bytes de archivo. El único que cambiaría es el tercer argumento index. Si este índice tuviera una longitud constante e independiente de w, con una longitud no excesivamente grande, podríamos almacenar los resultados de esa función para no tener que ejecutarlos repetidamente durante el bucle que opera los bytes de un archivo. Esta es la mejora que pretendemos implementar sobre el algoritmo anterior.

Empezaremos por analizar el resto parcial r'_i-1 que tiene una longitud w, el ancho del polinomio. Denominando ρ = r'_i-1 tenemos:

r'_i-1 = ρ = ρ₀ 10^w-1 + ρ₁ 10^w-2 + ... + ρ_w-3 10² + ρ_w-2 10 + ρ_w-1

Recuerde del apartado anterior que w≥d, pues si no lo fuera entonces ajustábamos el polinomio, y por tanto w, para que tuviera d dígitos. Entonces podemos separar el resto anterior en dos segmentos:

ρ_{[0, d]} = ρ₀ 10^w-1 + ... + ρ_w-d 10^d-1 ρ_{[d, w-d]} = ρ_w-d+1 10^d + ... + ρ_w-1

La parte iquierda ρ_{[0, d]} del resto anterior tiene d dígitos. Recuerde que en general definimos x_{[i, d]} como un segmento del número x tomando d dígitos a partir del dígito en la posición i-ésima. Cuando w = d la parte derecha ρ_{[d, w-d]} no tiene dígitos, pues ρ_{[d, 0]} significa tomar cero dígitos. En cualquier caso la parte derecha tiene el resto w-d. Esto significa que podemos expresar ρ como sigue:

ρ = ρ_{[0, d]} 10^w-d + ρ_{[d, w-d]}

Aplicamos esto a la recurrencia del algoritmo anterior:

r'_i = mod(0_d, y, x_{[i, d]} 10^w-d + r'_i-1) = mod(0_d, y, x_{[i, d]} 10^w-d + ρ) = mod(0_d, y, x_{[i, d]} 10^w-d + ρ_{[0, d]} 10^w-d + ρ_{[d, w-d]}) = mod( 0_d, y, ( x_{[i, d]} + ρ_{[0, d]} ) 10^w-d + ρ_{[d, w-d]} )

En los primeros apartados de este tema donde expusimos la función mod(x, y, z), vimos que mod(x, y, z) = mod(x, y) ^ z 10^d cuando trabajamos en arimética Mod2, siendo d la longitud del primer argumento. Como además mod(x, y) = mod(0_d, y, x 10^-d) entonces mod(x, y, z) = mod(0_d, y, x 10^-d + z) = mod(0_d, y, x 10^-d) ^ z 10^d.

Particularizando x como ( x_{[i, d]} + ρ_{[0, d]} ) 10^w y z como ρ_{[d, w-d]} llegamos a la siguiente recurrencia general:

r'_i = mod( 0_d , y , ( x_{[i, d]} + ρ_{[0, d]} ) 10^w-d ) + ρ_{[d, w-d]} 10^d

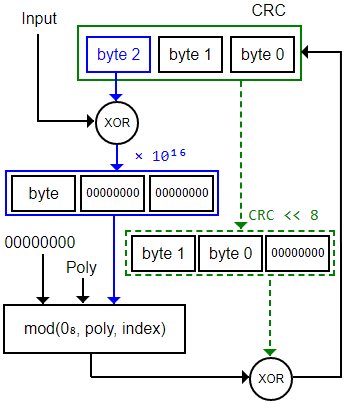
Para implementar el algoritmo en binario tendremos en cuenta que en esa recurrencia 10 es el binario 0b10 y las sumas son XOR. Un byte ocupará d = 8 bits. El esquema de la Figura representa la recurrencia anterior para un polinomio con un ancho w = 24 bits, 3 bytes.

El byte de la entrada es x_{[i, d]} en la iteración i-ésima. El top byte o byte de la izquierda del resto anterior es ρ_{[0, d]}. Es el byte 2 resaltado en azul en el esquema de la Figura. El byte de la entrada y el top byte tienen una longitud de d = 8 bits, un byte. He denominado este esquema como algoritmo CRC con índice de un byte, pues es el índice index = (x_{[i, d]} + ρ_{[0, d]}) 10^w-d el que se aplica a la función mod(0, poly, index). En el esquema vemos que el resultado del XOR se multiplica por 10¹⁶ puesto que w - d = 24 - 8 = 16.

Como x_{[i, d]} + ρ_{[0, d]} ocupa 8 bits, este término sólo tendrá 2⁸ = 256 valores posibles. Así que tendremos 256 índices entre 0·10^w-d y 11111111·10^w-d, lo que nos permitirá almacenarlos en un tabla y no tener que estar ejecutando mod(0, poly, index) con cada byte del bucle, algo que haremos en la mejora que presentaremos en un siguiente apartado.

Con el resultado de mod(0₈, poly, index) sumamos XOR con el CRC desplazado 8 bits a la izquierda. Veamos, la parte derecha del CRC es ρ_{[d, w-d]}, que son el byte 1 y byte 0 del esquema. Y calcular ρ_{[d, w-d]} 10^d = ρ_{[8, 16]} 10⁸ es como desplazar el CRC completo 8 bits a la izquierda. Finalmente el resultado de este XOR será el CRC para el siguiente paso del bucle.

Implementamos la recurrencia anterior:

function crcBytesBasic3({arrayBytes=[], width=0, poly="0"}){
    let widthBits = Math.max(width, 8);
    poly = "1"+hexToBin(poly).padStart(width, "0").padEnd(widthBits, "0");
    let crc = "0".repeat(widthBits);
    for (let i=0; i<arrayBytes.length; i++){
        let Byte = arrayBytes[i].toString(2).padStart(8, "0");
        let crcTopByte = shiftRight(crc, widthBits-8);
        //let crcTopByte = crc.substr(0, 8);
        let index = xor(crcTopByte, Byte) + "0".repeat(widthBits-8);
        let tab = mod("0".repeat(8), poly, index).substr(1, widthBits);
        let crcShift = shiftLeft(crc, 8);
        crc = xor(crcShift, tab).padStart(widthBits, "0");
    }
    crc = crc.substr(0, width);
    return crc;
}

En el código widthBits es w en la recurrencia y d = 8. Para recuperar el top byte, crcTopByte en el código, podríamos hacer crcTopByte = crc.substr(0, 8) teniendo en cuenta que estamos operando con Strings. Pero el objetivo final es convertir estos algoritmos en versiones que operen con números binarios. Por lo tanto la operación para recuperar el top byte debería ser algo como crc >>> (w-d), que para el ejemplo del esquema es crc >>> 16. Esto se consigue con shiftRight(crc, widthBits-8) usando nuestros binarios en strings.

El siguiente paso es calcular el índice index = (x_{[i, d]} + ρ_{[0, d]}) 10^w-d. Es la suma XOR del byte de la entrada y del top byte. Multiplicar por 10^w-d = 10¹⁶ equivale a agregar una cadena con 16 ceros, lo que hacemos concatenando "0".repeat(widthBits-8).

Ejecutamos la función mod(0₈, poly, index) que guardamos en la variable tab tras quitarle el primer bit que siempre resultará cero pues es que el resta del (1) del polinomio. El ancho del resto deber ser en cada momento widthBits, w en la recurrencia.

Calculamos ρ_{[d, w-d]} 10^d desplazando 8 bits a la izquierda crc << 8. En el código lo hacemos con crcShift = shiftLeft(crc, 8). Si N, P, Q son bits cero o uno, entonces el CRC sería de la forma NNNNNNNNPPPPPPPPQQQQQQQQ. Al desplazar 8 bits a la izquierda nos quedaría crcShift = PPPPPPPPQQQQQQQQ00000000 obteniendo los dos bytes finales del CRC al principio de crcShift.

Finalmente sumamos XOR el resultado del mod(0₈, poly, index) con el crcShift. Completamos con ceros a la izquierda dado que el XOR los elimina, resultando el nuevo CRC en este paso del bucle.

Finalizamos el bucle y devolvemos el CRC recortando los ceros que se añaden cuando width < 8, detalle que ya explicamos en el apartado anterior.

Veamos una traza que obtenemos en la herramienta con el CRC-24/LTE-A, con ancho w = 24 y polinomio 0x864CFB. Usaremos como entrada los códigos ASCI del string xyz. Los valores se presentan en hexadecimal para reducir espacio de texto:

Input: xyz ⇒ arrayBytes = [78,79,7A]
Width: 24
Poly: 0x864CFB ⇒  (1)864CFB

bytes = arrayBytes.length = 3
widthBits = Math.max(width, 8) = 24
poly 1864CFB adjusted with 0 zeros = 1864CFB
crc = 0

INPUT LOOP for i=0 to 2

i=0 ⇒ byte = arrayBytes[0] = 78
crcTopByte = (crc >> 16) & FF = 000000 & FF = 00
index = (crcTopByte ^ byte) + "0".repeat(widthBits-8) = (00 ^ 78) + "0".repeat(16) = 780000
tab = mod(00, poly, index) = mod(00, 1864CFB, 780000) = 71BD8B
crcShift = crc << 8 = 00 << 8 = 00
crc = crcShift ^ tab = 00 ^ 71BD8B = 71BD8B

i=1 ⇒ byte = arrayBytes[1] = 79
crcTopByte = (crc >> 16) & FF = 000071 & FF = 71
index = (crcTopByte ^ byte) + "0".repeat(widthBits-8) = (71 ^ 79) + "0".repeat(16) = 080000
tab = mod(00, poly, index) = mod(00, 1864CFB, 080000) = A18139
crcShift = crc << 8 = 71BD8B << 8 = BD8B00
crc = crcShift ^ tab = BD8B00 ^ A18139 = 1C0A39

i=2 ⇒ byte = arrayBytes[2] = 7A
crcTopByte = (crc >> 16) & FF = 00001C & FF = 1C
index = (crcTopByte ^ byte) + "0".repeat(widthBits-8) = (1C ^ 7A) + "0".repeat(16) = 660000
tab = mod(00, poly, index) = mod(00, 1864CFB, 660000) = 0C41D7
crcShift = crc << 8 = 1C0A39 << 8 = 0A3900
crc = crcShift ^ tab = 0A3900 ^ 0C41D7 = 0678D7

Adjust CRC = 0678D7 to width=24 bits:  crc = 0678D7 ⇒ 0x0678D7

En el siguiente tema sustituiremos la ejecución tab = mod(00, poly, index) por una tabla que memorice todos los valores posibles del índice.