Introducción al CRC
Introducción

La verificación por redundancia cíclica (CRC) es una técnica que agrega información redundante a un mensaje con objeto de verificar en la recepción si el mensaje ha sido modificado no intencionadamente durante la transmisión. El CRC no sirve para verificar la autenticidad del mensaje, pues cualquiera puede modificar el mensaje y la información redundante, con lo que en el destino el mensaje parecerá correcto. Pero si sirve para verificar cambios ocasionados por errores en la transmisión.
Cuando intenté entender los algoritmos que ya existen para obtener el CRC me encontré con trozos de códigos como el de la Figura. Se trata de obtener el CRC de forma recurrente con un algoritmo reflejado iterando por los bytes de un archivo, de tal forma que cuando finalicemos tendremos el CRC. Ese código forma parte del siguiente algoritmo que aparece al final del último tema, una implementación práctica para generar CRC-32/ISO-HDLC de 32 bits que se utiliza en ZIP o PNG entre otros:
const table = [];
function crc32IsoHdlc(arrayBytes=[]){
if (table.length===0) {
for (let i=0; i<256; i++){
let n = i;
for (let j=0; j<8; j++){
let shifted = n >>> 1;
n = (n & 1===1) ? shifted ^ 0xEDB88320 : shifted;
}
table.push(n);
}
}
let crc = 0xFFFFFFFF;
for (let Byte of arrayBytes){
crc = (crc >>> 8) ^ table[Byte ^ (crc & 0xFF)];
}
crc = crc ^ 0xFFFFFFFF;
if (crc<0) crc += 0xFFFFFFFF + 1;
return crc;
}Muchas veces puedo leer el código y entender algo de lo qué hace y cómo lo hace. Pero cuando empecé a intentar entender como generar CRC, los algoritmos como ese que consulté me parecieron tan confusos que no obtuve nada claro con una simple lectura. Esta serie de cuatro temas explica qué es el CRC y cómo generarlo sobre los bytes de un archivo. Y finalmente llegar a entender e implementar el algoritmo anterior. En algunos de los temas es necesario un poco de matemáticas pues no encontré otra forma de entenderlo.
Detección de errores mediante redundancia
Supongamos que tenemos que manejar unos identificadores numéricos de 8 dígitos. Por ejemplo, un número como 12345678. Estos valores van a ser transmitidos y pueden ocasionarse errores en la transmisión. Los errores más frecuentes podrían ser el cambio de un único dígito por otro y el intercambio de dos dígitos contiguos. Para detectar esos errores podríamos establecer un sistema de redundancia en la transmisión. Si transmitiéramos el mismo número dos veces, podría ser poco probable que se produjeran errores simultáneamente en ambos valores recibidos. En la recepción comprobaríamos si son iguales, descartándose en otro caso. Esto podría ser muy costoso si hubiera que transmitir muchos números. De todas formas no debemos descartar la idea de agregar información redundante a los datos durante la transmisión con el objetivo de la detección de errores.
Un primer intento sería reducir la cantidad de información redundante. Podríamos establecer un único dígito de verificación que ubicaríamos al final. Contaríamos el número de dígitos impares, con lo que transmitiríamos 123456784, donde hemos agregado el dígito 4 pues hay esos dígitos impares en 12345678. Esto podría detectar un cambio indebido si el número de impares es diferente. Pero no detectaría un "baile de números" como 21345678, dado que el número de impares sigue siendo el mismo.
El siguiente paso es incrementar un poco la información redundante sin que suponga repetir el valor. Supongamos que usamos el resto de la división del número entre otro fijo. Sea este divisor el número 23. La operación es calcular el resto de la división con el operador módulo: n mod 23, obteniendo restos con valores comprendidos entre 0 y 22. Para nuestro número de ejemplo tenemos 12345678 mod 23 = 14. Por lo tanto transmitiríamos 1234567814. En la recepción volveríamos a realizar la operación 12345678 mod 23 comprobando que el resto 14 es igual que el transmitido. Un error como el intercambio entre dos dígitos produciría en la recepción 21345678 mod 23 = 22, siendo detectado como error pues produce un resto 22 distinto del transmitido 14.
Esto, que básicamente se aplica en el dígito de control del DNI en España, no detecta todos los errores, pues en 99999999 números hay ⌊ 99999999 / 23 ⌋ = 4347826 números que generarán el mismo resto. Pero estarán en tramos de 23. Por ejemplo, 12345655 y 12345678 separados por 23 unidades producen el mismo resto 14. El error que supone recibir el final 55 en lugar de 78 es posible, pero poco probable teniendo en cuenta la hipótesis que hemos establecido de los tipos de errores más probables: cambio de un dígito por otro o intercambio de dos dígitos contiguos.
Comprobación con resto cero
Intentemos montar un sistema con el dígito de control anterior con los restos de la división entre 23 como antes, pero con una sistemática algo diferente. Supongamos que tenemos el mismo número 12345678 y vamos a calcularle el dígito de control. En primer lugar multiplicamos por 100 dado que el divisor 23 está en la centena, es decir, es menor de 100. Denominaremos al resultado 12345678 × 100 = 1234567800 con el término entrada aumentada. Obtenemos el resto 1234567800 Mod 23 = 20. Esto es así puesto que 1234567800 = 53676860 × 23 + 20. A continuación restamos ese resto del divisor resultando 23 - 20 = 3, valor que denominaremos CRC (código de redundancia cíclica). Por último agregamos este CRC al número a transmitir 1234567800 + 3 = 1234567803.
Cuando el receptor reciba este número realizará la operación 1234567803 mod 23 = 0 resultándole un resto cero, que le indicará que el mensaje se recibió correctamente. Se explica que resulte cero puesto que de estas operaciones se deduce que 1234567803 es un múltiplo de 23:
1234567803 = 1234567800 + 3 = 53676860 × 23 + 20 + 3 = 53676861 × 23 ⇒
⇒ 1234567803 mod 23 = 0
La formalización matemática para generar el CRC con aritmética decimal podría ser la siguiente, donde x es el mensaje, y es el divisor, w es el número de dígitos del divisor, x·10w es el mensaje aumentado con w ceros:
r = (x·10w) mod y ⇒ ∃ c : x·10w = y · c + r
crc = y - r
Si ahora aumentamos el mensaje con el CRC tendríamos x·10w + crc, deduciéndose que es un múltiplo de y por lo que el resto será cero:
x·10w + crc = (y · c + r) + y - r = y · (c + 1) ⇒
(x·10w + crc) mod y = 0
Hasta ahora hemos visto ejemplos en base decimal. Pero hemos de trabajar en base binaria. Supongamos que tenemos un mensaje con la letra "z" en ASCII, con representación binaria 01111010 (7A en hexadecimal). Para ser más precisos y siguiendo JavaScript, deberíamos escribir 0b01111010 para la representación binaria y 0x7A para la hexadecimal. Pero omitiremos 0b para abreviar cuando sea claro que estamos hablando de números binarios. Usaremos como divisor el binario 1011. La entrada aumentada será 011110100000, agregándose cuatro ceros dado que el mayor resto posible será 1010 (uno menos que el divisor) que tiene cuatro dígitos binarios.
Para obtener el resto usaremos la herramienta calculadora binaria con la operación MOD. Activando la traza en esa herramienta obtenemos la división siguiente, donde se omiten los ceros iniciales en el dividendo que son prescindibles:
11110100000 │ 1011
└────────────
10110001 …
1011
────
010001
1011
──────
0001100
1011
───────
00000010000
1011
───────────
00000000101 …Los puntos suspensivos indican en esa herramienta que la división no es entera. En todo caso lo único que nos interesa de esta operación es el resto 101. Siguiendo la sistemática que vimos en el apartado anterior, ahora restamos 1011 - 101 = 110 para obtener el CRC 110. Transmitimos 011110100000 + 110 = 011110100110 y observamos que entonces el resto es cero:
11110100110 │ 1011
└──────────
10110010
1011
────
010001
1011
──────
0001100
1011
───────
0000001011
1011
──────────
00000000000Al agregar el CRC al mensaje, este número viene a ser un múltiplo del divisor, resultando en un resto cero en la comprobación. En caso de que se modifique uno o más bits del mensaje, la comprobación no será cero. Observe que el segundo cociente 10110010 = 10110001 + 1 que responde al término (c + 1) que vimos más arriba, de tal forma que el segundo cociente multiplicado por el divisor resulta el dividendo aumentado con el CRC.
Este planteamiento es correcto y funciona. Pero no debemos olvidar que hemos de obtener el CRC de una entrada que normalmente no es tan corta como la expuesta en este ejemplo. Los CRC se generan sobre contenidos de archivos que pudieran ser muy grandes. Si intentamos usar la división con números en JavaScript, no podemos olvidar que no es posible usar números enteros mayores de 1FFFFFFFFFFFFF en hexadecimal, es decir, un 1 seguido de 52 bits, menos de 7 bytes. Para las operaciones binarias a nivel de bit JavaScript usa un registro con solo 32 bits, conformando enteros positivos y negativos entre los máximos valores decimales -2147483648 y +2147483647. En cualquier caso un archivo puede tener muchos bytes que superaran ampliamente cualquiera de esos límites.
Podríamos usar un algoritmo para ejecutar la división binaria sea cual sea la longitud del dividendo y/o divisor. De hecho en la herramienta que hemos señalado antes Web Tools online hay una para ello. Pero supone manejar operandos como String. Y eso también es costoso para dividendos muy largos. Así que hay que generar el CRC de una forma más eficiente. Y esto conlleva repasar previamente algunas cosas básicas sobre la aritmética binaria.
Aritmética binaria sin acarreos (Aritmética módulo 2)
En el tema Representación binaria de los números, de una serie de temas sobre los números en JavaScript, expuse las oparaciones aritméticas binarias. Hay unos ejemplos interactivos para convertir números o realizar operaciones. Ahora he trasladado y mejorado esos ejemplos en la herramienta Web Tools online. Toda esta parte de aritmética binaria son conceptos muy básicos, pero esenciales para entender posteriormente como generar el CRC de forma eficiente. Empezaremos por sumar binarios:
Suma normal 1100 + 1011 ───── 10111
La suma es tal que 0+0=0, 0+1=1, 1+0=1, 1+1=10, produciéndose en el último caso un resultado 0 con un acarreo 1. Esto funciona como en la aritmética decimal, acarréandose ese 1 para sumarlo con la siguiente columna.
Esta aritmética binaria se aplica a números enteros no negativos. Por lo tanto para restar x-y es necesario que x ≥ y. El resultado de restar binarios sería el siguiente:
Resta normal: Primer operando ≥ segundo operando
1100
- 1011
─────
1Para realizar una resta usamos la suma. Incluye la operación complementar a uno el segundo operando invirtiendo "0" por "1" y vicerversa, lo que se expresa en JavaScript con el signo "~". Así ~1011 = 0100. La operación de restar conlleva complementar a uno, acarrear 1, sumar normalmente y despreciar el último acarreo:
Para llevar a cabo la resta se realiza una suma: 1100 + 0100 Complemento a 1 el segundo operando ~1011 = 0100 + 0001 Acarreo 1 ─────10001 Al resultado de la suma se desprecia el primer 1
También podemos usar el concepto complemento a dos y así no lidiamos con acarreos. Se trata de complementar a uno y sumarle uno en único paso:
Resta 1100 + 0101 Complemento a dos de 1011 es ~1011 + 1 = 0100 + 1 = 101 ─────10001 Al resultado de la suma se desprecia el primer 1
Vease que igualmente procederíamos en la resta decimal. Calculemos con números decimales la resta 12-11 = 12 + 88 + 1 = 101, donde complementamos a 9 cada dígito del segundo operando y sumamos uno, despreciamos el acarreo de la izquierda que produce el resultado 12-11 = 1.
La suma en aritmética módulo 2 (aritmética Mod2 o aritmética sin acarreos) equivale a una suma normal pero se desprecian los acarreos. Esto equivale a una operación binaria XOR, que se representa en JavaScript con el signo "^". La tabla siguiente muestra los resultados de x^y indicándose el acarreo a, acarreo que se tiene en cuenta en la operación suma normal pero que se desprecia en el caso de operaciones suma Mod2:
x y x^y a ────────────── 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1
Esta operación es tan simple que con JavaScript podría conseguirse con una línea de código como: r[i] = (x[i]===y[i]) ? "0" : "1"; para cada pareja de dígitos i-ésimos, considerando los operandos como binarios en cadenas String.
Despreciando los acarreos la suma Mod2 de la operación 1100 + 1011 resulta así:
Suma equivale a operacion XOR (^) 1100 ^ 1011 ──── 0111 Resultado de 1100+1011 en Mod2
Veamos la resta 1100 - 1011 en aritmética Mod2. Ya vimos que en aritmética normal el complemento a dos de 1011, que podemos expresar como C(1011) se calcula como C(1011) = ~1011 + 1 = 0100 + 1 = 0101, pues si lo sumamos con el original y despreciamos el último acarreo resultará cero: 1011 + C(1011) = 1011 + 0101 = 10000. En Mod2 el único número que sumado Mod2 (con ^) nos resulte cero es el propio número: 1011 ^ C(1011) = 1011 ^ 1011 = 0000. Asi que en Mod2 C(1011) = 1011.
Ahora sabiendo que C(1011) = 1011 en aritmética Mod2, resolvamos la resta 1100 - 1011:
1100 ^1011 Complemento a dos en Mod2 de 1011 ──── 0111 Resultado de 1100-1011 en Mod2
Se observa que resulta lo mismo que 1100 + 1011. Como una resta Mod2 equivale a una suma Mod2, no se producirán acarreos y no importará que el primer operando sea menor que el segundo en el caso de las restas:
No se necesita primer operando ≥ segundo operando 1001 ^ 1011 ──── 0010
De hecho en aritmética Mod2 no tiene sentido hablar de orden de números. Y esto es clave cuando veamos el tema de la división, pues utiliza restas para obtener el resto para el CRC de forma eficiente. Veamos por último las dos operaciones que nos quedan, la multiplicación y la división.
Multiplicación normal
1100
1011
────────
+ 1100
+ 1100
+ 1100
────────
10000100
Multiplicación Mod2
1100
1011
───────
^ 1100
^ 1100
^ 1100
───────
1110100No nos detenemos en la multiplicación pues no influye sobre el CRC. Pero si la división siguiente realizada en aritmética normal:
División entera normal
1100101 │ 1011
└────────
-1011 1001 …
────
0001101
-1011
───────
0000010 …Vemos que se utilizan las restas normales, para lo cual es necesario que el primer operando de cada resta sea mayor que el segundo operando (el divisor). Mientras no lo sea vamos agregando dígitos del dividendo. Y la división Mod2 para los mismos operandos sería esta:
División Mod2
1100101 │ 1011
└──────
^1011 1110
────
01111
^1011
─────
001000
^1011
──────
0000111Ahora no hay restas sino operaciones XOR. Lo único que buscamos es completar un primer operando con cuatro dígitos cuyo primer dígito sea un uno, tras lo cual hacemos el XOR con el divisor. Y esto es clave para seguir buscando una forma eficiente de generar el CRC:
División Mod2: Si el divisor tiene N dígitos, vamos agregando dígitos del dividendo hasta completar N dígitos y cuyo primer dígito sea 1, entonces hacemos XOR con el divisor, continuando este proceso hasta acabar con los dígitos del dividendo.
Binarios en forma polinómica
Veamos ahora la razón de la denominación aritmética módulo 2 (aritmética Mod2). Por un lado un número binario puede expresarse como un polinomio con coeficientes 0 o 1 y potencias 2i. Por ejemplo, 0b1011 = 1·23 + 0·22 + 1·21 + 1·20. Intentemos realizar la suma normal de tres binarios 1011 + 0011 + 1101 utilizando polinomios:
+1011 1·23 + 0·22 + 1·21 + 1·20
+0011 0·23 + 0·22 + 1·21 + 1·20
+1101 1·23 + 1·22 + 0·21 + 1·20
───── ────────────────────────
???? 2·23 + 1·22 + 2·21 + 3·20 =
1·24 + 1·22 + 1·22 + (2+1)·20=
1·24 + 0·23 + 2·22 + 1·21 + 1·20 =
1·24 + 0·23 + 1·23 + 1·21 + 1·20 =
1·24 + 1·23 + 0·22 + 1·21 + 1·20 ⇒ 11011En lo anterior desarrollamos coeficientes y potencias hasta que los coeficientes sean alguno del conjunto {0, 1}, reagrupando y agregando coeficientes cero en los casos que no haya ninguno en esa potencia. Al final llegamos al resultado de coeficientes 11011 que es el resultado de la suma normal de 1011 + 0011 + 1101. Veamos ahora como sería esa suma en aritmética Mod2 usando también los polinomios:
^1011 1·23 + 0·22 + 1·21 + 1·20
^0011 0·23 + 0·22 + 1·21 + 1·20
^1101 1·23 + 1·22 + 0·21 + 1·20
───── ──────────────────────────────────────────
???? 2Mod2·23 + 1Mod2·22 + 2Mod2·21 + 3Mod2·20 =
0·23 + 1·22 + 0·21 + 1·20 ⇒ 0101Ahora a cada suma de coeficientes se le aplica el módulo 2, llegándose al resultado 0101. Obviamente todas las operaciones se simplifican con la aritmética Mod2.
Si en 0b1011 = 1·23 + 0·22 + 1·21 + 1·20 sustituimos 2i por xi nos quedará el siguiente polinomio P(x) = 1·x3 + 0·x2 + 1·x1 + 1·x0 = x3 + x + 1, siempre entendiéndose que x=2. Por eso en la documentación sobre CRC a veces veremos que se dice que se usa el polinomio P(x) como divisor. Por ejemplo, en la página CRC (Wikipedia) aparece una tabla con los CRC más utilizados. El segundo de esa lista es el CRC-3-GSM que utiliza este mismo polinomio x3 + x + 1.
Esta forma polinómica de expresar los números binarios es útil para demostraciones matemáticas, pues las operaciones aritméticas se resuelven con operaciones sobre polinomios. Así la suma normal de 1011 + 0011 + 1101 = 11011 se resolvería como sigue:
S = (x3 + x + 1) + (x+1) + (x3+x2+1) = 2x3 + x2 + 2x + 3 = x4 + x2 + x2 + 2 + 1 = x4 + 2x2 + x + 1 = x4 + x3 + x + 1 ⇒ S = 11011
Se desarrollan los coeficientes hasta que sean 2 y teniendo en cuenta que 2 = x se llega al mismo resultado final con los coeficientes 11011.
Estas representaciones sirven para demostraciones que se salen de mi alcance, como que un buen polinomio divisor para generar CRC debe cumplir:
- El divisor no debe ser divisible por x. Esta condición garantiza que se detecten todos los errores de ráfaga de una longitud igual o menor al divisor. Y dependiendo del divisor, en una proporción importante las que sean mayores que el divisor.
- El divisor debe ser divisible por x+1 para garantizar que se detecten todos los errores de ráfaga que afectan a un número impar de bits.
De todas formas en estos temas no voy a usar estas formas polinómicas para representar los números binarios en ningún caso. Representaremos la entrada del mensaje con una x que nada tiene que ver con la x=2 de esta representación polinómica. El polinomio divisor lo representaremos con una y.
Generando CRC con un algoritmo para calcular el resto de la división en aritmética Mod2
La formalización matemática para generar el CRC con aritmética módulo 2 sería igual que la de aritmética decimal, donde x es el mensaje, y es el divisor, w es el número de dígitos del divisor, x·10w es el mensaje aumentado con w ceros y donde en lugar de suma y/o resta se utiliza XOR:
r = (x·10w) mod y ⇒ ∃ c : x·10w = (y · c) ^ r
crc = y ^ r
Si ahora aumentamos el mensaje con el CRC tendríamos el mensaje aumentado x·10w ^ crc, demostrándose que es un múltiplo de y pues el resto será cero:
x·10w ^ crc = ((y · c) ^ r) ^ (y ^ r) = (y · c) ^ y ^ (r ^ r) = (y · c) ^ y = y · (c ^ 1) ⇒
(x·10w ^ crc) mod y = 0
Vemos que r ^ r = 0 porque el XOR de un binario consigo mismo resulta cero. Por otro lado (y · c) ^ y = y · (c ^ 1) pues esta expresión en aritmética Mod2 se comporta igual que en aritmética normal (y · c) + y = y · (c + 1).
Volvamos a nuestro ejemplo con la entrada "z" cuyo valor binario es 01111010. Volvemos a usar el divisor 1011. Agregamos la longitud del divisor, cuatro ceros, para obtener la entrada aumentada 11110100000. Obtengamos el resto con la división en aritmética Mod2:
11110100000 │ 1011
└──────────
11011001
^1011
────
01000
^ 1011
─────
0001110
^ 1011
───────
00001010
^ 1011
────────
00000001000
^ 1011
───────────
00000000011El CRC sería crc = y ^ r = 1011 ^ 11 = 1000. Si agregamos este CRC al mensaje obtendremos un cero en la división Mod2:
11110101000 │ 1011
└──────────
11011000
^1011
────
01000
^ 1011
─────
0001110
^ 1011
───────
00001011
^ 1011
────────
00000000000Observe como el segundo cociente 11011000 = 11011001 ^ 1 que es la expresión (c ^ 1) que vimos antes. Este segundo cociente multiplicado por el divisor nos devuelve el dividendo aumentado con el CRC.
Como en aritmética Mod2 no hay acarreos, todos los XOR en la división que hacemos con el divisor 1011 siempre tiene un cero en el dígito de la izquierda. Es lo mismo que decir que todos los restos parciales con un divisor de w dígitos tendrá a lo sumo w-1 dígitos significativos. Por ejemplo, si el divisor es 1011 los restos posibles van desde 0000 hasta 0111, siendo el bit de la izquierda siempre cero. Por eso w podría ser definido como el número de dígitos del divisor menos uno. Así nuestra definición formal sería de la siguiente forma, donde ahora omitimos la segunda línea crc = y ^ r explicándose el motivo más abajo:
crc = (x·10w) mod y ⇒ ∃ c : x·10w = (y · c) ^ crc
La comprobación de obtener un cero agregando este CRC a la entrada es como sigue:
x·10w ^ crc = ((y · c) ^ crc) ^ crc = (y · c) ^ (crc ^ crc) = (y · c) ^ 0 = y · c ⇒
(x·10w ^ crc) mod y = 0
Observe que crc ^ crc = 0, razón por la que omitimos la segunda línea de la definición crc = y ^ r. Podría haberse omitido también en la primera definición de este apartado, pero no en la definición en aritmética decimal, pues llegado a este punto tendríamos el término r + r ≠ 0 cuando r > 0, no pudiendo cumplir la condición de resto cero en todo caso.
Si ahora en el ejemplo agregamos tantos ceros como la longitud menos uno del divisor, lo que supone agregar tres ceros, obtenemos la entrada aumentada 1111010000. El resto con la división en aritmética Mod2 resulta el CRC 100:
1111010000 │ 1011
└─────────
1101100
^1011
────
01000
^ 1011
─────
0001110
^ 1011
───────
00001010
^ 1011
────────
0000000100Si agregamos este CRC 100 a la entrada y volvemos a dividir en aritmética Mod2 obtendremos un resto cero:
1111010100 │ 1011
└─────────
1101100
^1011
────
01000
^ 1011
─────
0001110
^ 1011
───────
00001011
^ 1011
────────
0000000000Esto que acabamos de ver no es otra cosa que el algoritmo de la división en aritmética módulo 2 para generar el CRC. Todo lo que sigue en este tema y siguientes se basa en este algoritmo.
Implementando los algoritmos de la división y del resto en aritmética módulo 2
Esta división módulo 2 o simplemente división Mod2 puede implementarse fácilmente con un algoritmo usando binarios en cadenas String en lugar de números. Esto significa que las operaciones no se limitan al máximo binario disponible en JavaScript. En primer lugar necesitaremos definir unas funciones previas que nos servirán para documentar este y siguientes apartados. Son las funciones shiftLeft, shiftRight, and y xor:
function shiftLeft(x="0", shift=0) {
return x.substr(shift) + "0".repeat(shift);
}
function shiftRight(x="0", shift=0){
return "0".repeat(shift) + x.substr(0, x.length-shift);
}
function and(x="0", y="0"){
if (x.length<y.length){
x = x.padStart(y.length, "0");
} else if (y.length<x.length){
y = y.padStart(x.length, "0");
}
return [...x].map((v, i) => v==="1" && y[i]==="1" ? "1" : "0").
join("").trimLeft().replace(/^0+/g, "").replace(/^(?:)$/, "0");
}
function xor(x="0", y="0"){
if (x.length<y.length){
x = x.padStart(y.length, "0");
} else if (y.length<x.length){
y = y.padStart(x.length, "0");
}
return [...x].map((v, i) => v===y[i] ? "0" : "1").join("").
replace(/^0+/g, "").replace(/^(?:)$/, "0");
}Las funciones shiftLeft(x, shift) y shiftRight(x, shift) actuan sobre un binario en String desplazando un número de shift bits a la izquierda y derecha respectivamente, rellenando con ceros los huecos en el lado opuesto. Así shiftLeft("101011", 1) resultará 010110. En esencia son equivalente a los operadores <<, >> y >>> sobre números binarios en JavaScript, aunque hay que matizar algunos detalles que comentaremos en un tema posterior.
La función xor(x, y) ejecuta la operación XOR sobre los operandos en binarios String. Es el equivalente al operador "^" de JavaScript sobre números binarios. Ya la habíamos comentado previamente. También exponemos la función and(x, y) que ejecuta la operación AND, pues se necesitará en un tema posterior. En ambos casos eliminamos los ceros iniciales, pues este es el comportamiento de esos operadores cuando se ejecutan con números binarios.
Ahora veamos el algoritmo de la división módulo 2:
function div(x="0", y="0") {
let q = "0", r = "0".padStart(y.length, "0");
for (let k=0; k<x.length; k++) {
r = xor(shiftLeft(r, 1), x[k]).padStart(y.length, "0");
if (r[0]==="1") {
q += "1";
r = xor(r, y).padStart(y.length, "0");
} else {
q += "0";
}
}
return [q, r];
}La sentencia r = xor(shiftLeft(r, 1), x[k]) desplaza un bit a la izquierda y rellena el bit de la derecha con el bit del argumento x que estamos manejando en el bucle. Rellenamos con ceros a la izquierda hasta completar la longitud del dividendo puesto que xor() los elimina. Se podría resolver con r = r.substr(1) + x[k], donde la suma concatena cadenas. Pero creo que debemos mantener una coherencia con las operaciones binarias, puesto que el objetivo es ver el aspecto teórico y luego reconvertir estos algoritmos sobre binarios String en equivalentes sobre números binarios.
En el código anterior partimos de un registro cuya longitud es la misma que el divisor. Quitamos el dígito izquierdo del registro e introducimos por la derecha un dígito del dividendo. En el momento en que el dígito de la izquierda del registro sea 1 procedemos a operar con XOR el registro y el dividendo y poner el resultado en el registro. Seguimos así hasta acabar con los dígitos del dividendo.
Se observa que operamos XOR cuando el dividendo tiene 4 dígitos y el primer dígito significativo es un 1. No importa ahora si el primer operando del XOR es menor que el segundo, puesto que la operación XOR en aritmética Mod2 no lo exige. Esto supone que con el divisor 1011 sólo se produzcan 8 posibles operaciones XOR, produciendo restos que tiene 3 dígitos como máximo:
1000 ^ 1011 = 011 1001 ^ 1011 = 010 1010 ^ 1011 = 001 1011 ^ 1011 = 000 1100 ^ 1011 = 111 1101 ^ 1011 = 110 1110 ^ 1011 = 101 1111 ^ 1011 = 100
Los restos van desde 000 hasta 111, con lo que se consigue el mismo efecto que con los restos de la división normal. La única diferencia es que con un divisor de 4 dígitos se obtienen restos de tres dígitos, cuando en la división normal se obtenían restos de hasta 4 dígitos, desde 0000 hasta 1010 para el caso del divisor 1011. Aún así la división Mod2 resulta tan eficiente que si queremos incrementar el número de restos posible sólo hemos de incrementar el divisor.
El algoritmo de la división Mod2 anterior devuelve también el cociente, algo que no necesitamos en la generación del CRC. Por eso usaremos el siguiente algoritmo del resto módulo 2 que calcula el módulo entre los argumentos x, y usando aritmética Mod2. Se pasa el argumento r puesto que en una mejora posterior lo necesitaremos, aunque ahora lo tomamos con el valor por defecto 0:
function mod(x="0", y="0", r="0") {
r = r.padStart(y.length, "0");
for (let k=0; k<x.length; k++) {
r = xor(shiftLeft(r, 1), x[k]).padStart(y.length, "0");
if (r[0]==="1") {
r = xor(r, y).padStart(y.length, "0");
}
}
return r;
}Con este código generamos el CRC de nuestro mensaje "z" aumentado con tres ceros, como la longitud del divisor. El siguiente esquema se genera con la herramienta usando la función MOD y la opción Mod2, ejecutando lo mismo que el código anterior. Se observa una columna con el valor inicial "0000". En cada iteración del bucle agregamos un bit a la derecha que quitamos del mensaje por la izquierda.
Generar CRC
1111010000 MOD 1011 ⇒
0000 1111010000
k= 0 0001 111010000
k= 1 0011 11010000
k= 2 0111 1010000
k= 3 1111 010000
1111 XOR 1011 = 0100
k= 4 1000 10000
1000 XOR 1011 = 0011
k= 5 0111 0000
k= 6 1110 000
1110 XOR 1011 = 0101
k= 7 1010 00
1010 XOR 1011 = 0001
k= 8 0010 0
k= 9 0100Transmitimos el mensaje agregando el CRC 100 al mensaje y comprobamos en la recepción que el resto es cero:
Comprobar CRC
1111010100 MOD 1011 ⇒
0000 1111010100
k= 0 0001 111010100
k= 1 0011 11010100
k= 2 0111 1010100
k= 3 1111 010100
1111 XOR 1011 = 0100
k= 4 1000 10100
1000 XOR 1011 = 0011
k= 5 0111 0100
k= 6 1110 100
1110 XOR 1011 = 0101
k= 7 1011 00
1011 XOR 1011 = 0000
k= 8 0000 0
k= 9 0000Generando CRC sobre bytes
Si orientamos este tema a generar el CRC sobre el contenido de un archivo, tenemos que hacer más eficiente el algoritmo anterior. En lugar de trabajar con bits deberíamos trabajar con bytes. Y es que extraer los bytes de un archivo con JavaScript es algo muy simple usando un Uint8Array, como puede comprobar en el tema que habla sobre como leer bytes de un archivo. En lo que sigue tendremos un ArrayBytes con esos bytes en formato Uint8Array.
Trabajaremos con algoritmos que ejecutan operaciones sobre binarios en String, pero no hay que olvidar que esto no es muy eficiente. El objetivo es entender el funcionamiento con la finalidad de convertir el último algoritmo obtenido en una versión que trabaje con números en JavaScript, salvando las particularidades que JavaScript tiene sobre los números binarios. Empecemos con una función para convertir un número hexadecimal en String en un binario en String:
function hexToBin(hex=""){
return [...hex].reduce((p,v) =>
`${p}${Number("0x"+v).toString(2).padStart(4, "0")}`, "").
replace(/^0+/, "");
}Exponemos esta conversión porque los parámetros para generar el CRC suelen venir en hexadecimal. Aunque luego hablaremos más sobre esto, por ahora nos centramos en generar el CRC con estos parámetros que ya hemos usando en los ejemplos anteriores:
- width=3 es el ancho en bits del CRC.
- poly=0x3 es el polinomio divisor para obtener el CRC exceptuando el primer 1. El valor viene en hexadecimal y su valor binario es 0b11 en binario.
El polinomio divisor realmente es 1011 en binario, pero cuando se definen los parámetros de los CRC se omite el primer 1. Así que si nos dan el polinomio 0x3 en hexadecimal lo convertimos a binario y a continuación ajustamos con ceros por la izquierda hasta completar el ancho width, anteponiendo finalmente un 1. Esto es la que hace la primera sentencia de la siguiente función crcBytesBasic():
function crcBytesBasic({arrayBytes=[], width=0, poly="0"}){
poly = "1" + hexToBin(poly).padStart(width, "0");
let bytes = arrayBytes.length;
let widthBytes = Math.ceil(width/8);
let widthLastByte = width-8*(widthBytes-1);
let crc = "0".repeat(width);
for (let i=0; i<bytes; i++){
let Byte = arrayBytes[i].toString(2).padStart(8, "0");
crc = mod(Byte, poly, crc);
}
for (let i=0; i<widthBytes; i++) {
let Byte = "0".repeat(i===widthBytes-1 ? widthLastByte : 8);
crc = mod(Byte, poly, crc);
}
return crc;
}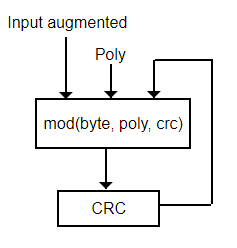
En la Figura puede ver un esquema de funcionamiento del algoritmo anterior. Lo exponemos porque posteriormente iremos modificando el algoritmo y también este esquema. Ahora vemos que la función mod(Byte, poly, crc) se ejecuta tantas veces como el número de bytes de la entrada más los aumentados. El CRC inicalmente es cero. Cuando se acaben el segundo bucle tendremos el CRC final en el registro.
En la herramienta podemos ejecutar una versión del algoritmo anterior, usando el generador CRC-3/GSM que produce una traza que vamos a separar en varias partes y comentar a continuación. En primer lugar se presentan los datos de entrada:
Input: z ⇒ arrayBytes = [01111010] Width: 3 Poly: 0x3 ⇒ (1)011
A continuación algunos cálculos previos, como el total de bytes del array de entrada. El ancho en bytes widthBytes del polinomio, que para el ejemplo con poly=(1)011 que tiene width=3 supone un byte. En widthLastByte calculamos los bits para la entrada aumentada. Con el polinomio (1)011 la entrada aumentada es 000 de 3 bits. Pero con otro polinomio más grande como (1)1000110011 con width=10 tenemos que widthBytes es 2 y widthLastByte es 2, es decir, la entrada aumentada serán dos bytes, teniendo el último byte un ancho efectivo de 2 bits.
bytes = arrayBytes.length = 1 widthBytes = Math.ceil(width/8) = 1 widthLastByte = width-8*(widthBytes-1) = 3 crc = 000
Primero ejecutamos el bucle que itera por el array de entrada. En el ejemplo el array sólo tiene un byte arrayBytes = [01111010]:
INPUT LOOP for i=0 to 1
i=0 ⇒ byte = arrayBytes[0] = 01111010
crc = mod(byte, poly, crc) = mod(01111010, 1011, 000) =
01111010 MOD 1011 ⇒
0000 01111010
k=0 0000 1111010
k=1 0001 111010
k=2 0011 11010
k=3 0111 1010
k=4 1111 010
1111 XOR 1011 = 0100
k=5 1000 10
1000 XOR 1011 = 0011
k=6 0111 0
k=7 1110
1110 XOR 1011 = 0101De la ejecución anterior obtenemos el resto 101 que nos servirá de registro para el siguiente bucle que itera por la entrada aumentada, un único byte con 3 bits 000:
INPUT AUGMENTED LOOP for j=0 to 0
j=0 ⇒ byte = "0".repeat(3) = 000
crc = mod(byte, poly, crc) = mod(000, 1011, 101) =
000 MOD 1011 ⇒
0101 000
k=0 1010 00
1010 XOR 1011 = 0001
k=1 0010 0
k=2 0100Finalmente obtenemos el resto 100. Vease que la ejecución de estos dos bucles, arrastrando el resto del primero como entrada de registro del segundo, es lo mismo que la ejecución que vimos al final del apartado anterior 1111010000 MOD 1011, que volvemos a reproducir a continuación señalando los dos bloques con distinto color:
1111010000 MOD 1011 ⇒ 0000 1111010000 k= 0 0001 111010000 k= 1 0011 11010000 k= 2 0111 1010000 k= 3 1111 010000 1111 XOR 1011 = 0100 k= 4 1000 10000 1000 XOR 1011 = 0011 k= 5 0111 0000 k= 6 1110 000 1110 XOR 1011 = 0101 k= 7 1010 00 1010 XOR 1011 = 0001 k= 8 0010 0 k= 9 0100
El algoritmo básico que hemos presentado debe aún mejorarse en muchos aspectos. En el próximo tema exponemos un poco de matemáticas para entender como funciona ese algoritmo y poder mejorarlo.