Recurrencias coeficientes variables
Diferenciar entre recursivos para calcular valores y costes
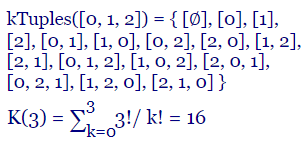
Esta serie de temas se dedica a generar el conjunto de sublistas para una función dada. Así, por ejemplo, el algoritmo combine2(n, k) que podemos ejecutar en la aplicación nos genera el conjunto de sublistas de tamaño k que son las combinaciones de un conjunto de tamaño n. El número de sublistas se obtiene con C(n, k) = n! / (k! (n-k!)). No cuestionamos esta fórmula, pues es un principio matemático que aceptamos sin más. Por otro lado el algoritmo que genera las sublistas tiene un coste calculado que ya vimos en ese tema con valor de T(n, k) = 2 C(n+1, k) - 1 con n≥k. Por lo tanto tenemos que diferenciar entre el cálculo de C(n, k) y el del algoritmo que implementamos y analizamos su coste con T(n, k), algoritmo para generar las sublistas de esa función.
Dicho esto ahora nos toca implementar y analizar algoritmos para generar las permutaciones. Pero antes analizaremos los siguientes algoritmos recursivos para calcular valores numéricos. Este primero es el que calcula el número de permutaciones de un conjunto con n elementos:
// P(n) = n * P(n-1)
function P(n){
if (n===0){
return 1;
} else {
return n * P(n-1);
}
}No vamos a analizarlo desde el punto de vista del coste, tal como hicimos en un tema anterior el factorial con función generadora, sino de su formulación matemática P(n) = n × P(n-1). Vea que es exactamente la misma recurrencia y recursivo que el usado para el factorial n! = n × (n-1)! puesto que P(n) = n!
Y vamos también a ver otro recursivo muy similar:
// K(n) = n * K(n-1) + 1
function K(n){
if (n===0){
return 1;
} else {
return n * K(n-1) + 1;
}
}La diferencia con el anterior es el +1. Este recursivo calcula el número de k-tuplas de un conjunto con n elementos. Más abajo veremos qué son las k-tuplas. Mientras vemos que su recurrencia matemática es K(n) = n × K(n-1) + 1, diferenciándose de las permutaciones solo en el sumando +1. Por esto uno podría estar tentado a pensar que si P(n) = n! entonces K(n) = n! + 1. Pero no es así, como observamos en el siguiente ejemplo donde ejecutamos ambos algoritmos para obtener valores para varios n:
Ejemplo: Algoritmos recursivo para calcular valores P(n) y K(n)
En las columnas P(n) y K(n) obtenemos los valores numéricos usando los recursivos anteriores. La otras dos columnas obtienen los valores usando esas expresiones matemáticas. Por un lado n! usa el algoritmo factorial(n) que es idéntico a P(n). El otro valor ∑k=0..n n!/k! calcula matemáticamente el número de k-tuplas, fórmula cerrada que trataremos de deducir en el resto de este tema.
Una fórmula cerrada para una recurrencia es una expresión matemática que no es recurrente y que produce el mismo resultado que la recurrencia. En definitiva, viene a ser lo que solemos denominar como solución del término general de la recurrencia.
Qué son las k-tuplas
Supongamos que tenemos el conjunto A= {0, 1, 2}. Las permutaciones de A son todos las sublistas ordenadas que podemos generar con todos los elementos de ese conjunto A. Su número es el resultado de P(3) = 3! = 6, resultados que se generan con el algoritmo permute(list) en la aplicación:
Mientras que las k-tuplas son todas las sublistas ordenadas que podemos generar con las permutaciones de todos los subconjuntos de ese conjunto A, resultados que generamos con otro algoritmo kTuples(list, 0) que usamos en la aplicación. En el tema siguiente explicaremos el motivo del segundo argumento que generaliza las K-Tuplas, pero por ahora vamos a ignorarlo.
[∅],
[0], [1], [2],
[0, 1], [1, 0], [0, 2], [2, 0], [1, 2], [2, 1],
[0, 1, 2], [1, 0, 2], [2, 0, 1], [0, 2, 1], [1, 2, 0], [2, 1, 0]
}
Se separan en líneas con el objetivo de ver lo siguiente: Los posibles subconjuntos de A se generan con C(n, k) usando el algoritmo combine(list, k) que usamos en la aplicación, iterando k=0 hasta k=n, incluyéndose el conjunto vacío ∅:
Para obtener las k-tuplas de A sólo tenemos que hallar las permutaciones de todos estos subconjuntos. Y su número es el resultado del recursivo K(3) = 16. En el resto de este tema buscaremos una fórmula cerrada para K(n) que nos permita calcular ese número sin usar el recursivo. Para ello tenemos que resolver la recurrencia K(n) = n K(n-1) + 1.
una secuencia (o lista ordenada) de n elementos, que viene a ser una permutación. Por otro lado designar el término general K(n) también es algo particular, aunque si P(n) cuenta las n-tuplas entonces K(n) cuenta las k-tuplas.
Recurrencias lineales con coeficientes variables
Supongamos que tenemos que resolver la siguiente recurrencia para calcular el número de k-tuplas:
| K(n) = { | 1 | si n=0 |
| n K(n-1) + 1 | si n>0 |
En primer lugar observamos el término n K(n-1) que indica que no puede usarse el modelo de ecuación de recurrencia de coeficientes constantes que vimos en el tema sobre recursivos que decía esto:
En ese modelo todos los coeficientes ai son constantes. Los tres ejemplos que vimos en el tema del enlace anterior, algunos de los cuáles hemos repetido en el segundo tema de esta serie, son todos con coeficientes constantes, obedeciendo a ese modelo:
- Factorial: T(n) = T(n-1) + 1
- Torres Hanoi: T(n) = 2 T(n-1) + 1
- Fibonacci: T(n) = T(n-1) + T(n-2) + 1
- Invertir array: T(n) = T(n-2) + 1
- Menor distancia: T(n) = T(n-1) + n
- Desordenar cadena: T(n) = 2 T(n-2) + 4n - 2
A todas las recurrencias anteriores puede aplicarse también la técnica de la función generadora (o generatriz) en series de potencias ordinarias (ordinary power series), tal como probamos para las tres primeras. Expresando nuestra recurrencia como el modelo tenemos tn - n tn-1 = 1, observamos que el segundo término tiene el coeficiente n no constante.
Antes de aplicar alguna técnica de función generadora, siempre podemos usar la técnica del despliegue o desarrollo de la recurrencia. Cuando la recurrencia no es muy compleja solemos llegar a un resultado. Vamos a intentarlo. Empezamos con la iteración i=n llegando hasta i=1, momento en el que alcanzamos el caso trivial K(0) = 1 y obtendremos la solución:
| = | n! | + | n! | + | n! | +...+ | n! | + | n! | + | n! | + | n! | = |
| 0! | 1! | 2! | (n-3)! | (n-2)! | (n-1)! | n! |
| = n! ∑k=0..n | 1 |
| k! |
Hemos llegado a una solución usando el desarrollo o despliegue de la recurrencia:
| K(n) = n! ∑k=0..n | 1 |
| k! |
Observe que hemos diferenciado una parte de las expresiones en color azul más claro. Se trata de que desarrollando la recurrencia P(0)=1, P(n) = n × P(n-1), lo mismo que decir 0!=1, n! = n × (n-1)!, entonces esas partes con color azul más claro sobrarían, llegando al final al resultado esperado:
Función generadora exponencial
A continuación vamos a intentarlo con otra función de generación diferente de la de serie de potencias que usamos en los temas anteriores. Partimos de la siguiente definición:
Evitamos índices negativos viendo que la recurrencia se inicia en n≥1:
Dividimos por (n+1)
| K(n+1) | = K(n) + | 1 |
| n+1 | n+1 |
Usaremos la función generadora exponencial siguiente que da lugar a una serie de potencias exponenciales (exponential power serie):
| Gn (x) = ∑n≥0 K(n) | xn |
| n! |
Si K(n) = 1 vemos el motivo de llamarse función exponencial (Wolframalpha), lo que es fácil de ver en el desplegable siguiente:
| ∑n≥0 | xn | = ex |
| n! |
Si como vimos en el apartado anterior P(n) = n! es el término general de las permutaciones, si aplicamos la función generadora exponencial a este término general tenemos:
| ∑n≥0 P(n) | xn | = ∑n≥0 n! | xn | = ∑n≥0 xn | = | 1 |
| n! | n! | 1-x |
observamos que obtenemos la serie geométrica, cuya secuencia es la unitaria 1, 1, 1, ..., siendo por tanto G(x) = 1/(1-x) la función generadora exponencial de las permutaciones y su serie es la serie exponencial de los factoriales, siendo su término general an = n!:
| ∑n≥0 n! | xn | = | 1 |
| n! | 1-x |
Esto nos da un pista de que la serie exponencial que estamos buscando para K(n) podría ser una fracción con un divisor 1-x. Vamos a buscarla a continuación.
Las condiciones iniciales son:
| G0 (x) = ∑n=0..0 K(n) | xn | = K(0) | x0 | = 1 |
| n! | 0! |
Aplicamos xn / n! a la recurrencia [1] y sumamos:
| ∑n≥0 | K(n+1) xn | = ∑n≥0 | K(n) xn | + ∑n≥0 | xn |
| (n+1) n! | n! | (n+1) n! |
Veamos el término de la izquierda de [2]
| ∑n≥0 | K(n) xn | = ∑n=0..0 | K(n) xn | + ∑n≥1 | K(n) xn | = |
| n! | n! | n! |
| = | K(0) x0 | + ∑n≥0 | K(n+1) xn+1 | = |
| 0! | (n+1)! |
| = 1 | + x ∑n≥0 | K(n+1) xn | = |
| (n+1) n! |
Despejando obtenemos
| ∑n≥0 | K(n+1) xn | = | 1 | ( G(x) - 1 ) |
| (n+1) n! | x |
Veamos el término de la derecha en [2] (Wolframalpha)
| ∑n≥0 | xn | = ∑n≥0 | xn | = ∑n≥0 | xn+1 x-1 | = |
| (n+1) n! | (n+1)! | (n+1)! |
| = | 1 | ∑n≥0 | xn+1 | = | 1 | ( - 1 + ∑n≥0 | xn | ) = | ex-1 |
| x | (n+1)! | x | n! | x |
Sustituyendo en [2]
| 1 | ( G(x) - 1 ) = G(x) + | ex - 1 |
| x | x |
De donde obtenemos la función generadora de la recurrencia dada:
| G(x) = | ex |
| 1-x |
Desarrollamos esta función con Taylor para ver si descubrimos la serie:
| G0(x) = | ex |
| 1-x |
| G1(x) = | ex (2-x) |
| (1-x)2 |
| G2(x) = | ex (x2-4x+5) |
| (1-x)3 |
| G3(x) = | ex (-x3+6x2-15x+16) |
| (1-x)4 |
| G4(x) = | ex (x4-8x3+30x2-64x+65) |
| (1-x)5 |
Particularizando para x=0 obtenemos la siguiente sucesión
Vemos que son los primeros términos que obtuvimos en el ejemplo interactivo del primer apartado para K(n). Pero supongamos que no sabemos nada acerca de esta sucesión y tenemos que determinar una expresión del término general. Y es en este punto donde puede uno atascarse. Pero hay una forma. Si escribimos esa secuencia en Wolframalpha nos expone una posible identificación de la secuencia que denomina OEIS A000522, web que tiene por título Enciclopedia On-line de secuencias de enteros. Esa web tiene también un buscador donde ponemos la secuencia y tratará de identificarla.
Ese enlace dice que es, entre otras cosas, la secuencia del número total de permutaciones de todos los subconjuntos de un conjunto con n elementos
. Expone, entre otras, la fórmula de la recurrencia a(n) = n × a(n-1) + 1, a(0) = 1 que es precisamente la recurrencia que estamos tratando. Expone esa web como función generadora exponencial (E.g.f: exponential generation function) precisamente la que hemos obtenido ex / (1-x).
Y, lo que es más importante, nos da muchos términos generales, entre los que extraemos los siguientes (cambiando a(n) por K(n) para ser coherentes con la denominación en este tema). En todos se aprecia una suma parcial k ∈ [0, n], exponiendo varias soluciones, de las cuáles una es la suma de 1/k!:
| K(n) = n! ∑k=0..n | 1 |
| k! |
Vea que ∑k≥0 1/k! = e. Con ese término general la función generadora queda así:
| G(x) = | ex | = ∑n≥0 ( n! ∑k=0..n | 1 | ) | xn |
| 1-x | k! | n! |
Se observa que para la recurrencia P(0)=1, P(n) = n × P(n-1) que calcula el factorial y que es similar a esta que estamos viendo prescindiendo del +1, como el término general es P(n) = n! entonces la función generadora no es otra cosa que la serie geométrica básica:
| G(x) = ∑n≥0 n! | xn | = | 1 |
| n! | 1-x |
Si aplicamos la función generadora a P(0)=1, P(n) = n × P(n-1) haríamos lo mismo que hicimos antes. Por ejemplo, en [2] sobraría el término de la derecha, con lo que llegaríamos a la expresión 1/x (G(x)-1) = G(x), de donde obtendríamos G(x) = 1/(1-x).
Producto de series, de Cauchy o convolución
Antes no pudimos deducir la solución usando Taylor y tuvimos que comprobarla en la página OEIS A000522. Veamos si es posible deducir directamente la solución anterior de la función generadora [3]:
| G(x) = | ex |
| 1-x |
Supongamos que tenemos estas dos funciones con sus series que ya conocemos:
| A(x) = | 1 | = ∑n≥0 xn |
| 1-x |
| B(x) = ex = ∑n≥0 | xn |
| n! |
Entonces si G(x) = A(x) B(x), siendo aj = 1 y bj = 1/j! solo tenemos que obtener el producto de esas series para obtener la solución. Se aplica el producto de series (de Cauchy o convolución) que ya expusimos en el primer tema:
Entonces siendo ak = 1 y bn-k = 1/(n-k)!
| G(x) = A(x) B(x) = ( ∑n≥0 xn ) × ( ∑n≥0 | xn | )= |
| n! |
| = ∑n≥0 ( ∑k=0..n | 1 | ) xn |
| (n-k)! |
Se observa que:
| ∑k=0..n | 1 | = ∑k=0..n | 1 |
| (n-k)! | k! |
Pues si desplegamos ambas sumas vemos que S1 = S2:
Entonces aplicamos esto y multiplicamos y dividimos por n! para igualarla con la serie exponencial. Este paso podría prescindirse, pero lo necesitamos para obtener el término general para K(n):
| G(x) = A(x) B(x) = ∑n≥0 ( n! ∑k=0..n | 1 | ) | xn |
| k! | n! |
llegamos a la misma solución:
| K(n) = n! ∑k=0..n | 1 |
| k! |
Si hubiésemos elegido las dos funciones al revés:
| A(x) = ex = ∑n≥0 | xn |
| n! |
| B(x) = | 1 | = ∑n≥0 xn |
| 1-x |
Entonces ak = 1/k! y bn-k = 1 pues todos los términos de esa serie son uno, llegando exactamente al mismo resultado del producto A(x) B(x) anterior, sin necesidad de usar la identidad que vimos en [4]:
| G(x) = A(x) B(x) = ( ∑n≥0 | xn | ) × ( ∑n≥0 xn )= ∑n≥0 ( n! ∑k=0..n | 1 | ) | xn |
| n! | k! | n! |
Puede comprobar en esta página de Wolframalpha que se llega al mismo resultado de la función generadora G(x) = ex / (1-x) multiplicando ambas series A(x) B(x). A partir de [5] podemos también tener este término general
| K(n) = n! ∑k=0..n | 1 |
| (n-k)! |
La función exponencial y las combinaciones
En la página OEIS A000522 que vimos antes también podemos representarlo en función de la k-permutación P(n, k). En nuestra aplicación Combine Tools preferimos hablar de variaciones V(n, k) en lugar de k-permutaciones. En cualquier caso P(n, k) = V(n, k) dado que sólo es un problema de denominación:
| = ∑k=0..n k! C(n, k) = ∑k=0..n | n! | = n! ∑k=0..n | 1 |
| (n-k)! | (n-k)! |
Se observa lo que comentamos en el apartado qué son las k-tuplas, siendo la suma de todas los términos P(k)×C(n, k) posibles para k ∈ [0, n]. Se evidencia fácilmente que:
| ∑k=0..n | 1 | = ∑k=0..n | 1 |
| (n-k)! | k! |
Pues si desplegamos ambas sumas vemos que S1 = S2:
De igual forma podemos hacer con la tercera identidad que vimos en el apartado anterior K(n) = ∑k=0..n P(k) C(n, k)
| G(x) = ∑n≥0 ( ∑k=0..n P(k) C(n, k) ) | xn | = |
| n! |
| = ∑n≥0 ( ∑k=0..n | k! C(n, k) | ) xn | = |
| n! |
| = ∑n≥0 xn × ∑n≥0 | k! C(n+k, k) | xn = |
| (n+k)! |
| = ∑n≥0 xn × ∑n≥0 | k! (n+k)! | xn = |
| (n+k)! k! (n+k-k)! |
| = ∑n≥0 xn × ∑n≥0 | xn | = A(x) B(x) = | ex |
| n! | 1-x |
Tras sumar k a n en el paso [6] para deshacer el producto de las dos series, hemos llegado a obtener el producto A(x) B(x) que vimos antes y que involucra a la misma función generadora G(x). Puede comprobar [6] en Wolframalpha. Podemos extraer también el término general en el paso previo tras sacar n! del grupo con paréntesis:
La función exponencial y las series binomiales
Si usamos Wolframalpha para evaluar G(x) = ex / (1-x) obtenemos esta serie que usa la serie binomial (-1+x)n:
| G(x) = | ex | =∑n≥-1 | (-1+x)n (-1) e |
| 1-x | (1+n)! |
Tratemos de demostrar esta identidad partiendo de la serie y llegando a G(x):
| ∑n≥-1 | (-1+x)n (-1) e | = |
| (n+1)! |
| = | (-1+x)-1 (-1) e | + ∑n≥0 | (-1+x)n (-1) e | = |
| (-1+1)! | (n+1)! |
| = | e | - e ∑n≥0 | (-1+x)n | = |
| 1-x | (n+1)! |
| = | e | - e ∑n≥0 | (-1+x)n+1 | = |
| 1-x | (n+1)! (-1+x) |
| = | e | + | e | ∑n≥0 | (-1+x)n+1 | = |
| 1-x | 1-x | (n+1)! |
| = | e | + | e | (- | (-1+x)0 | + ∑n≥0 | (-1+x)n | ) = |
| 1-x | 1-x | 0! | n! |
| = | e | + | e | (-1 | + ∑n≥0 | (-1+x)n | ) = |
| 1-x | 1-x | n! |
| = | e | ∑n≥0 | (-1+x)n | = |
| 1-x | n! |
| = | e | × | ex | = | ex |
| 1-x | e | 1-x |
En el paso [8] hacemos el cambio z = -1+x y resolvemos la serie exponencial que ya conocemos ∑n≥0 zn / n! = ez, que tras deshacer el cambio nos queda e-1+x = ex / e, logrando finalmente llegar a la G(x) esperada.
Esto demuestra la veracidad de la identidad obtenida en Wolfram Alpha, pero no nos dice nada acerca de la relación que hay entre la función exponencial y los binomiales. Empecemos por recordar el Binomio de Newton:
Si desplegamos ambos sumatorios
Estas dos sumas son iguales dado que C(n, k) = C(n, n-k)
| C(n, k) = | n! | ≡ C(n, n-k) = | n! |
| k!(n-k)! | (n-k)! k! |
De aquí pueden obtenerse las siguientes identidades con y=1 y con x=1 que ya hemos usado en temas anteriores, pero que también podemos usar con la alternativa n-k por la equivalencia anterior:
Como cuando k > n ⇒ C(n, k) = 0 podemos reducir las sumas a k ∈ [0, n]. Apliquemos estas series binomiales a nuestro problema partiendo de la situación que alcanzamos antes en [8], teniendo en cuenta que en (x+y)n ahora tenemos que y=-1. Lo aplicamos a la función f(x) = ex-1, de tal forma que luego podemos obtener G(x) = f(x) e / (1-x):
| f(x) = ex-1 = ∑n≥0 | (-1+x)n | = ∑n≥0 ∑k=0..n | C(n, k) xn-k (-1)k |
| n! | n! |
Puede comprobar que es cierto en Wolframalpha ¿Pero cómo se deduce esto? Como tenemos una suma en k=0..n intentemos separarla en un producto de series, pero antes apliquemos esto:
| C(n, k) | = | n! | = | 1 |
| n! | n! k! (n-k)! | k! (n-k)! |
Entonces
| f(x) = ∑n≥0 ∑k=0..n | C(n, k) xn-k (-1)k | = ∑n≥0 ∑k=0..n | xn-k | × | (-1)k | = |
| n! | (n-k)! | k! |
| = ( ∑n≥0 | xn-k+k | ) × ( ∑k≥0 | (-1)k | ) = |
| (n-k+k)! | k! |
| = ( ∑n≥0 | xn | ) × ( ∑k≥0 | (-1)k | ) = ex × | 1 | = ex-1 |
| n! | k! | e |
En la segunda línea hemos sumado k a n en la primera serie para deshacer el producto de series. Y a la suma de la derecha le ponemos índice k. Claramente la serie de la izquierda es ex como ya hemo visto.
Y la de la derecha es la serie para e-1:
| ∑k≥0 | (-1)k | = | 1 |
| k! | e |
como se observa en Wolframalpha. Entonces tenemos la función esperada:
| G(x) = | e | f(x) = | e | × | ex | = | ex |
| 1-x | 1-x | e | 1-x |
La función exponencial y la función gamma incompleta
En la página OEIS A000522 que vimos antes también expone otra solución usando la función gamma incompleta.
La función gamma incompleta se define de forma general como sigue:
| Γ(n, x) = (n-1)! e-x ∑k=0..n-1 | xk |
| k! |
Usando n+1 y x=1 nos queda
| Γ(n+1, 1) = n! e-1 ∑k=0..n | 1 |
| k! |
Si multiplicamos esto por e vemos que K(n) es exactamente la misma solución alcanzada en apartados anteriores:
| K(n) = n! ∑k=0..n | 1 |
| k! |
Entonces podemos expresar la serie de G(x) como sigue:
| G(x) = | ex | = ∑n≥0 ( e × Γ(n+1, 1) ) | xn |
| 1-x | n! |
Y el término general así:
Factorial ascendente y descentente. El símbolo de Pochhammer
Veamos ahora los factoriales ascendentes y descendentes. El factorial ascendente (rising factorial) o función de Pochhammer se define como el producto de n factores siguientes con n>0:
Mientras que el factorial descendente (falling factorial) se define como:
En ambos casos con n=0 se conviene que x0 = 1 y que x0 = 1.
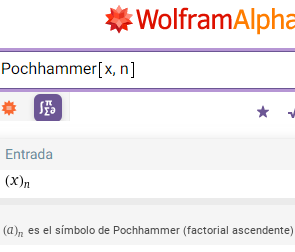
Hemos de tener cuidado con las notaciones x(n) para el ascendente y (x)n para el descendente, porque en lo relacionado con la función hipergeométrica (que veremos en el siguiente apartado) se usa (x)n para el ascendente (rising factorial), denominándolo el símbolo de Pochhammer. En Wolfram Alpha se implementa con (x)n = Pochhammer[x, n] refiriéndose al factorial ascendente xn.
En la Figura se observa la ejecución de Pochhammer[x, n] en Wolfram Alpha que traduce como (x)n. Pone al pie una nota que dice que (a)n es el símbolo de Pochhammer (factorial ascendente), refiriéndose realmente por tanto a x(n) = xn. Esta confusión podría evitarse usando xn y xn para el ascendente y descendente, pero así están las cosas. En la medida de lo posible procuraré usar la notación con sobrerayado y subrayado.
Wolfram Alpha también reconoce en lenguaje natural. pochhammer(x, n) como ascendente y factorialpower(x, n) como descendente.
Ambos factoriales se relacionan entre ellos así:
Están relacionados con el factorial ordinario así:
El factorial descendente está relacionado con las variaciones, pues V(n, k) = nk. Recordemos que las variaciones V(n, k) se suelen denominar como k-permutaciones P(n, k). Veamos como llegamos desde las variaciones hasta el factorial descendente:
| V(n, k) = C(n, k) P(k) = C(n, k) k! = | n! | = |
| (n-k)! |
| = | n·(n-1)·(n-2)···(n-k+1)·(n-k)! | = |
| (n-k)! |
Entonces podemos expresarlo así:
| nk = | n! |
| (n-k)! |
Por otro lado tenemos que:
| nk = | (n+k-1)! |
| (n-1)! |
Se deduce la relación con los coeficientes binomiales. Por un lado con el factorial descendente y las combinaciones sin repetición:
Con esto podemos expresar la fórmula que vimos en un apartado más arriba K(n) = ∑k=0..n k! C(n, k) también de esta forma:
Y por otro lado con el factorial ascendente y las combinaciones con repetición:
donde CR(n, k) = C(n+k-1, k) son las combinaciones con repetición que vimos en el tema anterior.
La función exponencial y la función hipergeométrica generalizada

Si usamos Wolframalpha para evaluar G(x) = ex / (1-x) obtenemos también esta serie basada en la función hipergeométrica generalizada pFq con p=2 y q=0:
| ex | =∑n≥0 2F0(1, -n;;-1) | xn |
| 1-x | n! |
Estudiemos esta solución, pues Wolfram Alpha las suele usar con frecuencia y nos pueden ayudar a identificar soluciones en otros problemas. En Wolframalpha vemos que la serie resultante de la función hipergeométrca 2F0(1, -n;;-1) genera la sucesión que vemos en la Figura.
En esa sucesión no aparece el valor para n=0 dado que siempre sera 1 en las funciones hipergeométricas generalizadas, tal como veremos después. Por lo tanto esa sucesión an = 1, 2, 5, 16, 65, 326, ... es la misma que se genera con K(n) que vimos en el ejemplo interactivo, así que tenemos otra representación para el término general:
Una serie hipergeométrica es una serie de potencias ∑n≥0 βn xn donde la relación entre dos términos es un cociente de polinomios, es decir, una función racional en n:
| βn+1 | = | A(n) |
| βn | B(n) |
La función exponencial genera una serie de este tipo:
| ex = ∑n≥0 | xn |
| n! |
vemos que tenemos A(n) = 1 y B(n) = n+1 puesto que
| βn+1 | 1 | n! | 1 | |||
| (n+1)! | ||||||
| = | = | = | ||||
| βn | 1 | (n+1)! | n+1 | |||
| n! |
La función hipergeométrica generalizada se define así:
| ∑n≥0 βn xn = pFq(a1,...,ap; b1,...,bq; x) = ∑n≥0 | a1n ··· apn | × | xn |
| b1n ··· bqn | n! |
El término ajn es el símbolo de Pochhammer o factorial ascendente. Aunque en esa página de Wikipedia y documentación sobre esto aparece escrita como (aj)n, es decir, como aparentemente el factorial descendente, aunque Wikipedida advierte que no es el estándar para el símbolo de Pochhammer.
Los coeficientes del polinomio A(n), con a0 = 1, es la sucesión An = 1, a1, ..., ap.
Es necesario que n+1 sea un factor de B(n). Si no lo fuera podemos multiplicar ambos polinomios por este factor. Si dividimos B*(n) = B(n) / (n+1), entonces los coeficientes Bn = 1, b1, ..., bq son los coeficientes del polinomio resultante B*(n) y no los de B(n). Vea que en ambos casos a0=1 y b0=1 no intervienen en la función.
En el ejemplo de la función exponencial tenemos que:
Con esto la función hipergeométrica generalizada que define la función exponencial es 0F0( ; ; x), tal como se observa en Wolframalpha, donde los dos primeros parámetros con los coeficientes se dejan en blanco pues p=0 y q=0:
| ex = ∑n≥0 | xn | = 0F0( ; ; x) |
| n! |
Apliquemos [10] a 2F0(1, -n;;-1) para ver si esto que vimos en Wolfram Alpha es cierto:
| ex | =∑n≥0 2F0(1, -n;;-1) | xn |
| 1-x | n! |
Vemos que p=2, q=0, a1=1, a2=-n, x=-1, entonces [10] queda así, donde hacemos el cambio n por k para no confundir con el n que aporta el término a2:
| ∑k≥0 | a1k ··· apk | × | xk |
| b1k ··· bqk | k! |
Entonces incluyendo los términos que conocemos:
| 2F0(1, -n;;-1) = ∑k≥0 1k (-n)k | (-1)k | ⇒ diverge |
| k! |
Si resolvemos en Wolframalpha nos dice que la suma diverge. Para evitarlo limitaremos el rango en k ∈ [0, n], pues sabemos que k varía en ese rango, y vemos lo que pasa:
| 2F0(1, -n;;-1) = ∑k=0..n 1k (-n)k | (-1)k | = e × Γ(n+1, 1) |
| k! |
Precisamente obtenemos la solución para K(n) que alcanzamos en un apartado más arriba que usaba la función gamma incompleta. Vea en Wolframalpha ese resultado alcanzado, apareciendo también la secuencia esperada 2, 5, 16, 65, 326, ....
Intentemos resolver ese resultado que nos ofrece de forma tan directa Wolfram Alpha. En un apartado anterior exponíamos estas identidades sobre factoriales ascendentes y descendentes, cambiando las variables x, n por n, k:
Si sustituimos esto en [11] nos queda:
| 2F0(1, -n;;-1) = ∑k=0..n | 1k (-n)k (-1)k | = |
| k! |
| = ∑k=0..n | k! k! C(n, k) | = ∑k=0..n k! C(n, k) = e × Γ(n+1, 1) |
| k! |
Y ese es el mismo resultado que alcanzamos para K(n) en un apartado anterior con el uso de las combinaciones y que es equivalente a e × Γ(n+1, 1) como ya vimos también.
En [12] como 1k = k! podemos ver otra solución para K(n) usando el factorial ascendente o símbolo de Pochhammer:
Función hipergeométrica confluente de segunda clase
En la página de Wikipedia y especialmente en Wolfram Mathworld, explican que 2F0(a, b; ; x) diverge, pero existe como un serie formal de potencias en 1/x, pudiendo usar la función hipergeométrica confluente de segunda clase U(a, b, x) con la siguiente transformación:
Con nuestros datos tenemos a = 1, b = -n, x = -1 por lo que (-1/x)a = 1, 1+a-b = n+2 y finalmente -1/x = 1:
En Wolframalpha puede comprobar ese resultado, que viene a ser otra solución equivalente de nuestro problema:
Resumen: Soluciones equivalentes de una recurrencia
A modo de resumen y para la recurrencia dada K(n) = n K(n-1) + 1, K(0) = 1 hemos deducido en este tema todas estas soluciones equivalentes, siendo K(n) el término general de la serie:
| ex | = ∑n≥0 K(n) | xn |
| 1-x | n! |
| Deducido con | K(n) |
|---|---|
| Despliegue recurrencia | ∑k=0..n n! / k! |
| Producto de series | ∑k=0..n n! / (n-k)! |
| Combinaciones | ∑k=0..n k! C(n, k) |
| Factorial descendente | ∑k=0..n nk |
| Factorial ascendente (símbolo Pochhammer) | ∑k=0..n (-n)k (-1)k |
| Función gamma incompleta | e × Γ(n+1, 1) |
| Función hipergeométrica generalizada | 2F0(1, -n; ; -1) |
| Función hipergeométrica confluente de segunda clase | U(1, n+2, 1) |
Este tema puede parecer muy largo, pero me ha servido para conocer formas equivalentes de representar la solución a una recurrencia. Y es algo necesario en caso de usar recursos como Wolfram Alpha, que a veces nos da la solución involucrando alguno de estos conceptos.