Permutaciones de Heap
El algoritmo de Heap para generar permutaciones

Las permutaciones de una lista con n elementos distintos son todas las sublistas ordenadas con n elementos distintos que se pueden generar. Se denota generamente como P(n). Su valor es P(n) = n!
El algoritmo de Heap genera las permutaciones de forma más eficiente que el que hemos usado en el tema anterior. Se basa en generar cada permutación desde una previa intercambiando una pareja de elementos cada vez. En la Figura puede ver como se van intercambiando posiciones desde la lista inicial [0, 1, 2] generando las permutaciones {[0, 1, 2], [1, 0, 2], [2, 0, 1], [0, 2, 1], [1, 2, 0], [2, 1, 0]}. Implementamos este algoritmo con permute2(list):
function permute2(list=[], n=list.length, result=[]){
if (n<=1) {
iter += 1;
if (withCopyCost) iter += list.length;
result.push(copy(list));
} else {
iter += 1;
for (let j=0; j<n; j++){
iter += 1;
permute2(list, n-1, result);
if (j<n-1) {
if (n%2===0){
[list[j], list[n-1]] = [list[n-1], list[j]];
} else {
[list[0], list[n-1]] = [list[n-1], list[0]];
}
}
}
}
return result;
}Se puede encontrar otro algoritmo equialente que apenas se diferencia con el anterior y que tiene el mismo coste. La diferencia está en el bucle y en la parte de intercambio, no necesitando la comprobación de paridad n%2===0 aunque se producen intercambios infructuosos con los mismos índices. En cualquier caso el número de iteraciones es exactamente el mismo en ambos casos. Este es el algoritmo del que vamos a analizar su coste en este tema y así evitamos manejar la paridad de la iteración en el coste:
function permute3(list=[], n=list.length, result=[]){
if (n<=1) {
iter += 1;
if (withCopyCost) iter += list.length;
result.push(copy(list));
} else {
iter += 1;
for (let j=n-1; j>-1; j--){
iter += 1;
[list[j], list[n-1]] = [list[n-1], list[j]];
permute3(list, n-1, result);
[list[j], list[n-1]] = [list[n-1], list[j]];
}
}
return result;
}Analizaremos permute3(list). La definición de la recurrencia de coste queda así:
| T(n) = { | 1 | si n≤1 |
| n T(n-1) + n + 1 | si n>1 |
Este algoritmo ya lo expuse en el tema Permutar con el algoritmo de Heap hace años. Como es una recurrencia de coeficientes variables, hice un despliegue o desarrollo de la recurrencia para obtener la solución. Replico aquí lo mismo que expuse en ese tema. En la iteración n al inicio tenemos:
Iteración n-1:
Iteración n-2:
Iteración n-3:
Seguimos hasta alcanzar la iteración 2
Lo resaltado en azul tiene los términos del rango [2..n-1]. El caso trivial es T(1) = 1, con lo que los dos resaltes en amarillo son iguales:
Vemos que lo resaltado en amarillo sigue la secuencia de la serie con rango [2..n-1] resaltada en azul, por lo que podemos agruparlos en una serie que se incrementa en un término con el rango ahora [2..n]:
Deducimos el término general como n!/(n-j+1)! con j ∈ [2..n] quedando:
| T(n) = 1 + 2 ∑j=2..n | n! |
| (n-j+1)! |
Observe en Wolframalpha que se obtiene la secuencia 1, 5, 19, 81, 411, 2473, 17319, ... para n≥1. Para n=0 esta recurrencia no ofrece valor alguno, siendo establecido por la definición como T(0) = 1. Se obtiene la misma secuencia si resolvemos directamente la recurrencia en Wolframalpha.
Algoritmo de Heap con función generadora
Vamos a obtener esa solución usando una función generadora o generatriz. Partimos de:
Incrementamos índices para evitar negativos:
Dividimos entre n+1:
| T(n+1) | = T(n) + | n+2 |
| n+1 | n+1 |
Usamos la función generadora exponencial con el caso base desplazado en n=1 (ver lo que comentamos en el tema desplazamiento del caso base):
| Gn (x) = ∑n≥1 T(n) | xn |
| n! |
Las condiciones iniciales son las siguientes, de las que sólo necesitaremos G1(x):
| G0 (x) = ∑n=0..0 T(n) | xn | = T(0) | x0 | = 1 |
| n! | 0! |
| G1 (x) = ∑n=1..1 T(n) | xn | = T(1) | x1 | = x |
| n! | 1! |
Aplicamos xn / n! a la recurrencia [1] y sumamos:
| ∑n≥1 | T(n+1) xn | = ∑n≥1 | T(n) xn | + ∑n≥1 | (n+2) xn |
| (n+1) n! | n! | (n+1) n! |
El término de la izquierda en [3] es:
| ∑n≥1 | T(n+1) xn | = ∑n≥1 | T(n+1) xn+1 x-1 | = | 1 | ∑n≥1 | T(n+1) xn+1 | = |
| (n+1) n! | (n+1)! | x | (n+1)! |
| = | 1 | ∑n≥2 | T(n) xn | = | 1 | ( - | T(1) x1 | + ∑n≥1 | T(n) xn | ) = |
| x | n! | x | 1! | n! |
| = | 1 | ( G(x) - x | ) |
| x |
El término después del signo igual en [3] es obvio:
| ∑n≥1 | T(n) xn | = G(x) |
| n! |
Y ahora el término de la derecha en [3]:
| ∑n≥1 | (n+2) xn | = ∑n≥1 | (n+1) xn | + ∑n≥1 | xn | = |
| (n+1) n! | (n+1)! | (n+1)! |
| = ∑n≥1 | xn | + | 1 | ∑n≥1 | xn+1 | = |
| n! | x | (n+1)! |
| = ∑n≥1 | xn | + | 1 | ∑n≥2 | xn | = |
| n! | x | n! |
| = - | x0 | + ∑n≥0 | xn | + | 1 | (- | x0 | - | x1 | + ∑n≥0 | xn | ) = |
| 0! | n! | x | 0! | 1! | n! |
| = -1 + ex + | -1 - x + ex | = |
| x |
| = -2 + ex + | -1 + ex | = |
| x |
Obviamente el término ∑n≥0 xn/n! = ex. Sustituyendo [4], [5] y [6] en [3]:
| 1 | ( G(x) - x ) = G(x) - 2 + ex + | ex-1 |
| x | x |
De donde:
| G(x) = | (ex-1) (x+1) | = | x ex | + | ex | - | 2 | + 1 |
| 1-x | 1-x | 1-x | 1-x |
El penúltimo sumando de la derecha en [7] es una geométrica:
| 2 | = 2 ∑n≥0 xn | = 2 ∑n≥0 n! | xn | = 2 ( | x0 | + ∑n≥1 n! | xn | ) = |
| 1-x | n! | 0! | n! |
| = 2 + 2 ∑n≥1 n! | xn | = |
| n! |
Los otros dos términos en [7] se identifican con las K-Tuplas para valores de k=0 y k=1:
| G(x, k) = | xk ex | = ∑n≥0 K(n, k) | xn |
| 1-x | n! |
donde K(n, k) es, entre otras formas, así:
| K(n, k) = ∑j=0..n-k | n! |
| j! |
Entonces con k=0 y k=1 nos queda:
| ex | + | x ex | = ∑n≥0 ( ∑j=0..n | n! | ) | xn | + ∑n≥0 ( ∑j=0..n-1 | n! | ) | xn | = |
| 1-x | 1-x | j! | n! | j! | n! |
| = ∑n≥0 ( - | n! | + 2 ∑j=0..n | n! | ) | xn | = |
| n! | j! | n! |
| = ∑n≥0 ( - 1 + 2 ∑j=0..n | n! | ) | xn | = |
| j! | n! |
| = ( - 1 + 2 ∑j=0..0 | 0! | ) | x0 | + ∑n≥1 ( - 1 + 2 ∑j=0..n | n! | ) | xn | = |
| j! | 0! | j! | n! |
| = 1 + ∑n≥1 ( - 1 + 2 ∑j=0..n | n! | ) | xn |
| j! | n! |
Agrupando [8] y [9] en [7] tenemos la serie de G(x), donde se observa que los tres términos por fuera de los sumatorios se anulan:
| G(x) = 1 + ∑n≥1 ( - 1 + 2 ∑j=0..n | n! | ) | xn | - 2 - 2 ∑n≥1 n! | xn | + 1 = |
| j! | n! | n! |
| = ∑n≥1 ( -2n!-1+2 ∑j=0..n | n! | ) | xn |
| j! | n! |
El término general es:
| T(n) = -2n! - 1 + 2 ∑j=0..n | n! |
| j! |
Observe en Wolframalpha que se obtiene la secuencia 1, 5, 19, 81, 411, 2473, 17319, ... para n≥1, la misma que obtuvimos en el apartado anterior.
Hacemos un ajuste manual con el sumatorio para reflejar el índice j≥2 del algoritmo y poder compararlo con la solución alcanzada en el apartado anterior:
| T(n) = - 2n! - 1 + | 2 n! | + | 2 n! | + 2 ∑j=2..n | n! |
| 0! | 1! | j! |
obteniéndose finalmente
| T(n) = 2n! - 1 + 2 ∑j=2..n | n! |
| j! |
Se comprueba que tiene la misma secuencia en Wolframalpha, por lo que esta solución es equivalente a la que alcanzamos en el apartado anterior con el desarrollo de la recurrencia:
| T(n) = 1 + 2 ∑j=2..n | n! |
| (n-j+1)! |
Demostrar la equivalencia de ambas soluciones usando las K-Tuplas
En el tema de las K-Tuplas demostramos esta igualdad:
| K(n, k) = ∑j=0..n-k | n! | = ∑j=0..n-k | n! |
| j! | (n-j-k)! |
Si tomamos n+1 y k=0 tenemos la siguiente igualdad:
| ∑j=0..n+1 | (n+1)! | = ∑j=0..n+1 | (n+1)! |
| j! | (n-j+1)! |
ajustando los índices
| (n+1)! | + (n+1) ∑j=0..n | n! | = | (n+1)! | + (n+1) ∑j=0..n | n! |
| (n+1)! | j! | 0! | (n-j+1)! |
simplificando:
| 1 + (n+1) ∑j=0..n | n! | = (n+1)! + (n+1) ∑j=0..n | n! |
| j! | (n-j+1)! |
despejando el primer sumatorio:
| ∑j=0..n | n! | = - | 1 | + | (n+1)! | + | n+1 | ∑j=0..n | n! | = |
| j! | n+1 | n+1 | n+1 | (n-j+1)! |
| = - | 1 | + n! + ∑j=0..n | n! |
| n+1 | n-j+1 |
Ajustamos índices j≥2 en ambos lados:
| n! | + | n! | + ∑j=2..n | n! | = - | 1 | + n! + | n! | + | n! | + ∑j=2..n | n! |
| 0! | 1! | j! | n+1 | (n+1)! | n! | (n-j+1)! |
Entonces tras simplificar todo lo que podamos:
| ∑j=2..n | n! | = 1 - n! + ∑j=2..n | n! |
| j! | (n-j+1)! |
Si sustituimos este sumatorio en [10] tendremos que llegar a [11]:
| T(n) = 2n! - 1 + 2 ∑j=2..n | n! | = |
| j! |
| = 2n! - 1 + 2 ( 1- n! + ∑j=2..n | n! | ) | = |
| (n-j+1)! |
| = 1 + 2 ∑j=2..n | n! |
| (n-j+1)! |
Siendo esta solución la esperada para demostrar que [10] es lo mismo que [11].
Coste de copia del Algoritmo de Heap
El análisis del coste visto en apartados anteriores no contempla el coste de copiar los resultados parciales. Dado que cuando tenemos un resultado parcial al llegar al caso base hemos de traspasarlo al array de resultados, si no hacemos una copia estaremos almacenando la misma referencia y, por tanto, el resultado al final contendría n! resultados iguales que la última permutación generada. Para evitarlo hacemos una copia del array de cada resultado parcial:
...
if (n<=1) {
iter += 1;
if (withCopyCost) iter += list.length;
result.push(copy(list));
} else {
...Como hay n! permutaciones para un conjunto de n elementos, entonces el coste de copiarlos será n n!, quedando el término general con coste de copia de esta forma para ambas soluciones equivalentes:
| T(n) = n n! + 2n! - 1 + 2 ∑j=2..n | n! |
| j! |
| T(n) = n n! + 1 + 2 ∑j=2..n | n! |
| (n-j+1)! |
Coste asintótico del Algoritmo de Heap
Cuando analicé este algoritmo hace años en coste asintótico del algoritmo de Heap encontré que el coste sin copia era del orden del factorial T(n) ∈ O(n!). Pero con coste de copia habría que sumar n n! por lo que se elevaba a T(n) ∈ O((n+1)!).
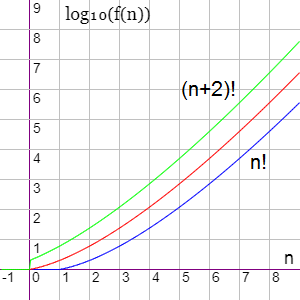
El algoritmo básico que presentamos en el tema anterior tenía un coste asintótico de T(n) ∈ O((n+2)!), con o sin copia, pues ese algoritmo siempre produce resultado parciales copiados. En cualquier caso el algoritmo de Heap reduce desde (n+2)! hasta n! en el caso de coste sin copia y hasta (n+1)! con copia. No parece mucho reducir una unidad de orden en el factorial, pero tal como comentamos en ese tema, si por ejemplo bajamos de 9! = 362880 a 8! = 40320 supone evitarnos 322560 iteraciones: cerca del 89% menos. Con ningún otro tipo de coste, ni siquiera el exponencial, supone tanto ahorro bajar una unidad de orden de coste. Esto se observa en la Figura.
Además en el enlace a algoritmo de Heap que pusimos al principio dice que en 1977 Robert Sedgewick concluyó que el algoritmo de Heap era el más eficiente para generar permutaciones en aquel momento. Y aunque no expone lo contrario, suponemos que esto sigue siendo cierto al menos con computación convencional.