Curvas Bezier cúbicas en SVG
Puntos de control de Bezier cúbica para aproximar arco de circunferencia
En el tema anterior vimos que se necesita un polígono de 5 o más puntos para conseguir una aproximación aceptable de la Bezier cuadrática a un arco de circunferencia, aproximación que de todas formas se podía apreciar desviaciones con una ampliación de 500 veces. Usando una Bezier cúbica conseguiremos una mejor aproximación incluso con polígonos de menos puntos.
La Figura representa dos puntos consecutivos P y Q de un polígono regular. En este caso es de 5 lados, pero haremos los cálculos para cualquier polígono con n≥3 lados. El ángulo α = 2π/n se divide en dos partes iguales de α/2, dado que la recta OF es la bisectriz que corta en dos partes el arco de circunferencia PBQ en color rojo.
La curva de Bezier cúbica se aproxima al arco de circunferencia si somos capaces de ubicar correctamente los dos puntos de control C y D. Es importante observar que las tangentes a la circunferencia en los puntos P y Q también serán tangentes a la curva de Bezier. Esos segmentos están ubicados sobre la recta que pasa por QF y PF respectivamente, siendo F el punto de réplica o envolvente que ya vimos en el tema anterior. Esto será clave para resolver el problema, como veremos.
El problema es localizar los puntos de control C y D. Pero como queremos una solución genérica, buscaremos la distancia de control desde el centro del polígono a uno cualquiera de los dos puntos de control, pues d = OC = OD dado que impondremos la condición de que que el arco de Bezier coincidirá con el de la circunferencia en la mitad de ese arco, con lo que los puntos de control serán simétricos respecto a la bisectriz. La otra variable necesaria será el ángulo de control δ, pues con la distancia y ese ángulo podremos ubicar un punto en cualquier lugar del plano.
Empezamos exponiendo la ecuación de Bezier cúbica, siendo t ∈ [0, 1]:
B(t) = (1-t)3 P + 3t(1-t)2 C + 3t2(1-t) D + t3 QExpresada en coordenadas XY:
x(t) = (1-t)3 xp + 3t(1-t)2 xc + 3t2(1-t) xd + t3 xq y(t) = (1-t)3 yp + 3t(1-t)2 yc + 3t2(1-t) yd + t3 yqLos puntos P y Q son cualquier pareja de puntos consecutivos del polígono de n lados que están separados α = 2π/n grados. Si P está en k×α grados, el siguiente Q estará en (k+1)×α grados, con k ∈ {0, 1, 2, ..., n-1}. Tomando el radio r = OP = OQ = OB, los puntos P, Q están ubicados en estos lugares:
xp = r cos(k α) yp = r sin(k α) xq = r cos((k+1) α) yq = r sin((k+1) α)El punto medio (x, y) sobre la bisectriz ha de cumplir la ecuación de la circunferencia de radio r:
x = r cos(k α + α/2) y = r sin(k α + α/2)Como la bisectriz corta en dos semiarcos de circunferencias iguales, el parámetro de la Bezier debe ser t=1/2 estando al centro del rango [0, 1], así que ese punto (x, y) también cumplirá:
x = 1/8 xp + 3/8 xc + 3/8 xd + 1/8 xq y = 1/8 yp + 3/8 yc + 3/8 yd + 1/8 yqLa primera simplificación es tomar la primera pareja de puntos con k=0. No olvidar que lo que estamos buscando es la distancia de control y el ángulo de control, valores que serán aplicables a cualquier pareja de puntos:
xp = r yp = 0 xq = r cos(α) yq = r sin(α) x = r cos(α/2) y = r sin(α/2)Tomar k=0 simplifica el primer punto P que cae sobre el eje X a una distancia del radio del polígono y ayudará posteriomente a resolver más cosas. Las ecuaciones de Bezier ahora quedan así:
r cos(α/2) = 1/8 r + 3/8 xc + 3/8 xd + 1/8 r cos(α) [1] r sin(α/2) = 3/8 yc + 3/8 yd + 1/8 r sin(α) [2]Necesitamos establecer más condiciones para resolver los puntos de control C = (xc, yc) y D = (xd, yd). La recta que pasa por PC es tangente a la circunferencia en el punto P y por tanto perpendicular al eje X, eje donde se ubica el punto P pues tiene un ángulo de cero grados dado que hemos dicho que k=0. Como P también pertenece a la Bezier, entonces P = (xc, yc) = (r, yc). De la ecuación [1] anterior obtenemos xd:
r cos(α/2) = 1/2 r + 3/8 xd + 1/8 r cos(α) ⇒ xd = 8/3 r cos(α/2) - 8/6 r - 1/3 r cos(α) [3]También condicionamos la tangente en el otro punto, la recta que pasa por QD, que podemos obtener dado que conocemos el punto P y el punto F que es el punto de réplica o envolvente que ya vimos en el tema anterior. Como PF es perpendicular al eje X, el triángulo OPF es rectángulo y por tanto el ángulo β es complentario de α/2 con lo que β = π/2 - α/2:
tan(β) = OP / PF = r / PF ⇒ (xf, yf) = (r, r/tan(β)) = (r, r tan(α/2))Donde aplicamos tan(β) = tan(π/2 - α/2) = 1/tan(α/2). Teniendo los puntos Q y F determinamos la recta que pasa por ambos, siendo la pendiente:
m = (yf - yq) / (xf - xq) = (r tan(α/2) - r sin(α)) / (r - r cos(α))La ecuación de la recta que pasa por Q con pendiente m es y = m (x-xq) + yq que usaremos para ubicar el punto (xd, yd):
yd = ((r tan(α/2) - r sin(α)) / (r - r cos(α))) (xd-r cos(α)) + r sin(α)Resolvemos con wolframalpha.com obteniéndose la simplificación x cot(α) + y = r csc(α) que también podemos poner como sigue si multiplicamos ambos lados por sin(α):
xd cos(α) + yd sin(α) = rForma alternativa de resolución
Podemos llegar al mismo resultado xd cos(α) + yd sin(α) = r planteándolo de otra forma. Por un lado vemos que las distancias desde el origen a cada punto de control deben ser iguales pues los puntos de control son simétricos respecto a la bisectriz. Una vez suprimiendo las raíces cuadradas nos queda:
OC = OD ⇒ r2 + yc2 = xd2 + yd2Por el mismo motivo de simetría las distancias PC y QD también deben ser iguales. PC = yc puesto que es la tangente perpendicular al eje X. QD lo obtenemos restando las coordenadas de esos puntos, recordando que conocemos las coordenadas del punto Q:
PC = QD ⇒ yc2 = (xd - xq)2 + (yd - yq)2 = (xd - r cos(α))2 + (yd - r sin(α))2Si sustituimos este valor de yc2 en la primera ecuación
r2 + (xd - r cos(α))2 + (yd - r sin(α))2 = xd2 + yd2Resolvemos con Wolframalpha.com obteniéndose la siguiente forma alternativa:
r = xd cos(α) + yd sin(α)Sustituyendo el valor de xd obtenido antes en [3] obtenemos ahora yd:
(8/3 r cos(α/2) - 8/6 r - 1/3 r cos(α)) cos(α) + yd sin(α) = r ⇒ yd = r/sin(α) + 8/6 r cos(α)/sin(α) + 1/3 r cos2(α)/sin(α) - 8/3 r cos(α/2) cos(α)/sin(α)Podriamos usar este punto (xd, yd) para obtener la distancia y ángulo de control. Pero podemos sustituir este yd en [2] con la esperanza de obtener yc y ver si se simplifica la otra pareja (xc, yc) = (r, yc), dado que xc ya tiene un valor simple:
r sin(α/2) = 3/8 yc + 3/8 (r/sin(α) + 8/6 r cos(α)/sin(α) + 1/3 r cos2(α)/sin(α) - 8/3 r cos(α/2) cos(α)/sin(α)) + 1/8 r sin(α) ⇒ yc = 4/3 r tan(α/4)Ese resultado tan simple lo he obtenido también en wolframalpha.com asumiendo, como es el caso, que r, α, yc son positivos. Por lo tanto el primer punto de control C tiene estas coordenadas:
(xc, yc) = (r, 4/3 r tan(α/4))Y de ahí obtenemos la distancia de control para ambos puntos, pues es la misma, como el resultado de (xc2+yc2)1/2:
distancia control = r (1 + (4/3 tan(α/4))2)1/2Y el ángulo de control como el resultado de α/2 - tan-1(yc / xc) para un punto es el siguiente, siendo negativo para el otro punto:
ángulo control = α/2 - tan-1(4/3 tan(α/4))A medida que incrementamos los lados del polígono la distancia de control se acerca al radio y el ángulo de control a cero, posicionándose ambos puntos de control en el punto medio del arco de circunferencia, lugar donde el arco de Bezier se igualará con el de la circunferencia con un polígono de infinitos lados:
limα→0 1/3 r (9 + 16 tan^2(α/4))1/2 = r limα→0 α/2 - tan-1(4/3 tan(α/4)) = 0La tabla siguiente resume los valores para polígonos de 3 a 6 lados y radio la unidad. Con el enlace a la web wolframalpha.com se puede comprobar estos resultados:
| lados (n) | α=2π/n | xc=r | yc | Distancia de control | Ángulo de control | Test |
|---|---|---|---|---|---|---|
| 3 | 2π/3 | 1 | 4/271/2 ≈ 0.7698 | (43/27)1/2 ≈ 1.26198 | ≈22.4109 ° | 3 lados |
| 4 | π/2 | 1 | 4/3 (21/2-1) ≈ 0.552285 | 1/3 (57-32×21/2)1/2 ≈ 1.14237 | ≈16.0888 ° | 4 lados |
| 5 | 2π/5 | 1 | 4/3 (1-2/51/2)1/2 ≈ 0.433226 | 1/3 (25-32/51/2)1/2 ≈ 1.08981 | ≈12.5765 ° | 5 lados |
| 6 | π/3 | 1 | 8/3-4/31/2 ≈ 0.357266 | 1/3 (121-64×31/2)1/2 ≈ 1.0619 | ≈10.3399 ° | 6 lados |
Una vez obtenidos la distancia de control y el ángulo de control, los usaremos en la aplicación para determinar los puntos de control de la curva Bezier cúbica para cada pareja de puntos del polígono, creándose el arco de curva con el comando:
Cxc yc xd yd xq yqIteramos por los puntos de la lista de puntos, llegando al punto num. Obtenemos el ángulo entre ese y el anterior, siendo θ = k×α, un múltiplo de α, ángulo al que restamos y sumamos el ángulo de control para el primer y segundo punto respectivamente. Los puntos de control se devuelven en el array [[xc, yc], [xd, yd]]:
let [x, y] = [this.listaPuntos[num].x, this.listaPuntos[num].y];
let [xa, ya] = [this.listaPuntos[num-1].x, this.listaPuntos[num-1].y];
let [xm, ym] = [xa + (x-xa)/2, ya + (y-ya)/2];
let theta = Math.atan2(ym-centroY, xm-centroX);
distanciaControl = Math.abs(distanciaControl);
anguloControl = anguloControl*Math.PI/180;
if (curva==="Q") {
...
} else { //curva==="C"
let xc = centroX + distanciaControl*Math.cos(theta - anguloControl);
let yc = centroY + distanciaControl*Math.sin(theta - anguloControl);
let xd = centroX + distanciaControl*Math.cos(theta + anguloControl);
let yd = centroY + distanciaControl*Math.sin(theta + anguloControl);
plus = [[xc, yc], [xd, yd]];
}
Representación gráfica de la curva Bezier cúbica
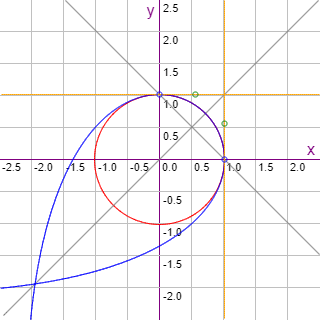
En la Figura podemos ver una representación gráfica de la curva de Bezier cúbica (en color azul) aproximándose al arco de circunferencia (color rojo), tomando un polígono de cuatro lados centrado en el origen y de radio la unidad.
Los puntos marcados con un pequeño círculo en azul son los dos vértices del polígono de cuatro lados que se ubican en el primer cuadrante. Los de color verde son los dos puntos de control: uno en (xc, yc) = (1, 4/3 (21/2 - 1)) y el otro en (xd, yd) = (4/3 (21/2 - 1), 1).
Esta aproximación a la circunferencia es mejor que la que conseguíamos con la Bezier cuadrática.
Trazar la gráfica matemática de la Figura
edita-funcion: color="red"; t=0..2*PI; x = cos(t); y = sin(t); #color="gray"; y = -x+1; #color="gray"; y=x; #color="blue"; t=-5..5;a=1;b=0;c=1;d=(4/3)*(SQRT2-1);f=1;g;0;h=1; x = pow(1-t,3)*a + 3*t*pow(1-t,2)*c + 3*pow(t,2)*(1-t)*d + pow(t,3)*g; y = pow(1-t,3)*b + 3*t*pow(1-t,2)*d + 3*pow(t,2)*(1-t)*f + pow(t,3)*h; #color="orange";y=1 #color="orange";x=1;y=-3..3 #color="blue";t=0..2*PI;r=0.04; x = 1+r*cos(t); y = r*sin(t); #color="blue";t=0..2*PI;r=0.04; x = r*cos(t); y = 1+r*sin(t); #color="green";t=0..2*PI;r=0.04; x = 1+r*sin(t); y = 0.552285+r*cos(t); #color="green";t=0..2*PI;r=0.04; x = 0.552285+r*sin(t); y = 1+r*cos(t); _anchoxy: 320_altoxy: 320_zoomx: 65_zoomy: 65_usar-colores: 0
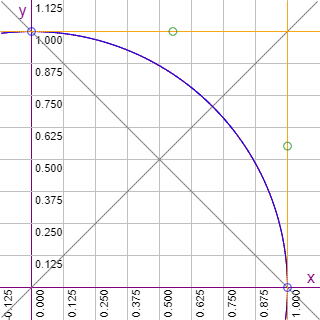
En la Figura ampliamos el cuadrante derecho hasta 256 veces. Vemos que no se observa una desviación de la Bezier con respecto al arco de circunferencia. Compare esta situación con la ampliación que hicimos en el tema anterior con la cuadrática.
La Figura es un SVG con cuatro curvas. La primera es un arco de circunferencia con el comando "A" construida con dos semiarcos de 180° cada uno y de color rojo. Sobre ella hay una curva de Bezier cúbica en un polígono de 3 lados en color azul, otra de 4 lados en color verde y finalmente una de 5 lados en color negro. La superposición es perfecta en este nivel de ampliación, mezclándose los colores en una especie de gris. Las cúbicas aparentan circunferencias perfectas. Pero no lo son.
Puede importar el código del SVG de la Figura en el editor SVG:
<svg viewBox="0 0 16 16" width="320" height="320">
<path d="M15 8A7 7 0 1 0 1 8A7 7 0 1 0 15 8z" stroke="red" fill="none" stroke-width="0.01"></path>
<path d="M15 8C15 13.39 9.17 16.76 4.5 14.06C-0.17 11.37 -0.17 4.63 4.5 1.94C9.17 -0.76 15 2.61 15 8z" stroke="blue" fill="none" stroke-width="0.01"></path>
<path d="M15 8C15 11.87 11.87 15 8 15C4.13 15 1 11.87 1 8C1 4.13 4.13 1 8 1C11.87 1 15 4.13 15 8z" stroke="green" fill="none" stroke-width="0.01"></path>
<path d="M15 8C15 11.03 13.05 13.72 10.16 14.66C7.28 15.59 4.12 14.57 2.34 12.11C0.55 9.66 0.55 6.34 2.34 3.89C4.12 1.43 7.28 0.41 10.16 1.34C13.05 2.28 15 4.97 15 8z" stroke="black" fill="none" stroke-width="0.01"></path>
</svg>
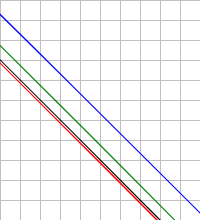
Hemos de ampliar mucho, hasta 30000 veces en la Figura, para observar las desviaciones. La roja es la construida con arcos de circunferencias. Las otras son cúbicas de 3 lados (azul), 4 lados (verde) y 5 lados (negra).
La Figura es una captura de pantalla del editor SVG. No pongo el propio SVG por si algún navegador no lo reproduce adecuadamente. Las versiones actualizadas de los navegadores si lo representan. De todas formas puede aplicar viewBox="12.93 3.02 0.0534 0.0534", reducir el grueso de línea de todas las curvas a stroke-width="0.0002" y aplicar un zoom de 30000. O bien puede ver el SVG en otra página usando este enlace al SVG con curvas Bezier cúbicas.