Construyendo un polígono regular

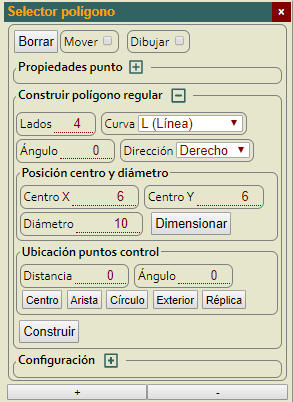
El Selector de área y polígono es una utilidad que tiene ya algunos años. Se trata de situar un área que se sobrepone sobre un elemento HTML permitiendo mover y cambiar el tamaño de ese elemento. En el modo de polígono podemos crear uno ubicando puntos que se unían con líneas SVG (elemento <line>). Ahora lo he mejorado para unir los puntos con elementos <path>, tanto formando una línea (comando "L") como curvas de Bezier cuadráticas ("Q"), cúbicas ("C") y arcos ("A") de circunferencias. Una utilidad que contempla son unos controles para construir un polígono regular como se observa en la Figura.

He mejorado el componente Selector de área y polígono a raíz de la creación de un editor SVG dentro del marco de herramientas Webtools online. Así podemos crear fácilmente SVG polígonales con el elemento <path>, editando los puntos con el componente selector de polígono. Puede ver una página con información de ese editor SVG.

En este tema veremos como unir los puntos del polígono con curvas de Bezier cuadráticas, usando el comando "Q" en lugar de "L". En el tema siguiente veremos las Bezier cúbicas usando el comando "C". El tercero lo dedicaremos a calcular los puntos de control para dibujar un arco de circunferencia con curvas de Bezier partiendo de dos puntos del plano.

En la Figura puede ver como construimos un polígono regular de 4 lados en el editor SVG. Con los controles de posición del centro y diámetro ubicamos el centro en el punto (6, 6) y el diámetro de 10 unidades. El botón "Dimensionar" calcularía esos valores para que el polígono quede centrado en el SVG. Unimos los puntos con líneas usando el comando "L". La parte de ubicación de puntos de control sólo aplica a las curvas de Bezier, ignorándose para el comando "L".

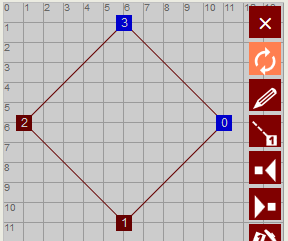
El primer punto del polígono se dibuja en el ángulo de rotación cero seleccionado, teniendo en cuenta que en HTML+CSS los ángulos avanzan en el sentido del reloj, al revés que como es usual hacerlo en matemáticas. Por lo tanto con un ángulo cero el primer punto está a la derecha del centro del polígono en dirección horizontal con 0 grados de separación, cayendo en esa línea horizontal. Los puntos siguientes se ubican con una separación de α = 360°/lados de separación.

La dirección de avance es derecha, avanzando en el sentido de las agujas del reloj. La dirección izquierda lo haría al revés. El polígono construido en el editor SVG es el de la Figura, donde el punto 0 es el primero y el 3 el último, ambos con fondo azul indicando este hecho y que cierran el polígono. Con el botón actualizamos el SVG generando el siguiente código:

<svg viewBox="0 0 24 24" width="480" height="480">
    <path d="M11 6L6 11L1 6L6 1z" stroke="currentcolor" fill="none"></path>
</svg>
    

Puntos de control interesantes en una curva de Bezier Cuadrática

Bezier cuadráticas

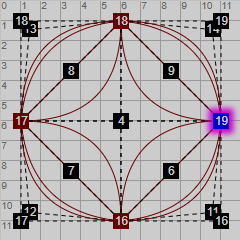Imagen no disponible

Curvas Bezier cuadráticas que unen los 4 puntos de un polígono: centro, arista, círculo y exterior.

Si unimos los puntos del polígono con curvas de Bezier cuadráticas podemos configurar la ubicación de los puntos de control, estableciendo la distancia de control desde el centro del polígono en la dirección de la bisectriz. Esta es la línea que divide el ángulo α = 360°/lados que forman dos puntos consecutivos del polígono.

También hay un ángulo de control de ubicación del punto de control, que es el ángulo que forma con la bisectriz. De esa forma la combinación de ese ángulo con la distancia nos pemite ubicar el punto de control en cualquier punto del plano. Está pensado para utilizarlo con Bezier cúbicas, por lo que en este tema para obtener los puntos interesesantes de una Bezier cuadrática no será utilizado.

Los puntos interesantes para una Bezier cuadrática se ubican sobre la bisectriz entre dos puntos consecutivos. Se calculan con los botones que vemos representados en la Figura 1: Centro, Arista, Círculo, Exterior y Réplica. En la primera imagen de la serie de cinco imágenes adjuntas a este párrafo se observan los puntos 16 y 19 que forman un lado del polígono. Realmente es la pareja 15-16, pues el 19 pertenece a la pareja 18-19 y cae justo encima del 15. El centro es el punto de control 4, la arista es el 6, la circular es el 11 y el exterior es el 16.

Si observamos uno a uno cada punto interesante, en la primera imagen de la serie verá los cuatro arcos tomando como distancia el propio centro del polígono. Los puntos del polígono son 0, 1, 2, 3 y 4 que cae sobre el 0. La curva de Bezier entre dos puntos se establece en el punto final, así que tenemos cuatro puntos de control 1, 2, 3 y 4 ubicados en este caso todos en el centro.

La imagen siguiente presenta la distancia Arista, cayendo los puntos de control en el centro de la arista que une dos puntos consecutivos del polígono. Cuando los puntos se alinean con el de control la curva de Bezier pasa a ser una recta. En la imagen siguiente se presenta la distancia Círculo, definida como la distancia necesaria desde el centro para que cada arco se aproxime al arco de circunferencia entre dos puntos consecutivos del polígono. Posteriormente veremos que es una aproximación y no un arco exacto de circunferencia. En la imagen última se presenta la distancia Exterior. Coincide con la de Réplica o envolvente con polígonos de 4 lados. Se observa que las líneas que unen los puntos de control replican y envuelven el polígono interior.

El problema es cómo calcular la ubicación de cada uno de los puntos de control interesantes. Partimos del esquema de la Figura que representa una pareja P-Q de puntos consecutivos de un polígono de cuatro lados. Los puntos P y Q forman un ángulo α con respecto al punto O, centro del polígono. En el gráfico ese ángulo es de 90° que corresponde a un cuadrante de un polígono de 4 lados, pero podría ser cualquier polígono de 3 o más lados. Los puntos de control interesantes están situados sobre la bisectriz que divide el ángulo de 90°, con los puntos O, M, C, E, F. Aunque realmente lo que estamos buscando es medir las distancias con respecto al centro del polígono: OM, OC, OF, OE.

Empezaremos localizando el punto M que está situado en el centro de la arista PQ, siendo la línea OE es la bisectriz que divide el ángulo α en dos partes iguales. Se observa claramente que OM = OP × cos(α/2) = OR × cos(α/2) pues OP = OR.

Váyamos ahora por el punto C. El arco de curva PQ se aproxima al arco de circunferencia de radio OR = OP = OQ, de tal forma que el punto de control C de círculo nos servirá para situar la curva cuadrática de Bezier sobre ese arco rojo de la circunferencia. Vemos que OC = OR + RC = OR + MR, admitiendo que MR = RC para cualquier ángulo α con el objeto de hacer coincidir el arco de la curva con el de la circunferencia, siendo el punto C el que mejor aproxima ambos.

Como por otro lado MR = OR-OM = OR-OR×cos(α/2) entonces sustituyendo en la anterior expresión OC = OR+MR = OR+OR-OR×cos(α/2) = OR×(2-cos(α/2)). En el siguiente apartado demostramos este valor aplicando directamente la fórmula de Bezier cuadrática, deduciéndose que la hipótesis MR = RC era correcta para obtener una aproximación a la circunferencia.

Otro punto de control interesante es el E que denominamos exterior, observándose que simplemente es el doble de la distancia OM, es decir, OE = 2×OM = 2×OR×cos(α/2).

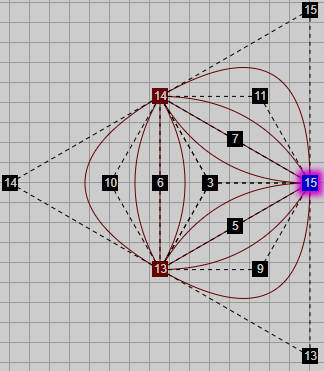
Hay otro punto control F que podemos obtener en la herramienta que es el de envolvente o réplica, pues se obtiene el polígono replicado con las líneas que unen los puntos de control. En el caso anterior con un ángulo de 90°, que se corresponde con un polígono de 4 lados, el punto de control exterior E coincide con el de réplica F. Pero para un polígono con otro ángulo como el de la Figura, el de réplica está situado más lejos que el exterior.

En esa imagen vemos que para la bisectriz que divide el ángulo que forman dos puntos consecutivos del polígono en color marrón, por ejemplo el 13 y 14, encontramos el punto de control (negro) del centro marcado con el 3, el de arista con el 6, el exterior con el 10 y el de réplica con el 14. Se observa que los puntos de control de réplica 13, 14 y 15 en color negro forman el polígono de 3 lados con líneas discontinuas que envuelve y replica el polígono interior 13, 14, 15 de puntos marrones y líneas continuas también de 3 lados.

La fórmula para obtener la distancia desde el centro del polígono al de réplica es OF = OR / cos(α/2). Podemos deducirlo siguiendo el esquema que reproduce dos puntos consecutivos P y Q del polígono de 3 lados anterior:

Los puntos O, M, F se corresponden con los puntos de control de la imagen anterior con números 3, 14 y 10 respectivamente. Por un lado vemos que QM = OQ × cos(β) = OQ × sin(α/2). Además sabemos que el ángulo β es complementario de α/2 dado que OMQ forma un triángulo rectángulo pues OF es la bisectriz. Se deduce que tan(α/2) = 1/tan(β). El ángulo β también es el mismo que se forma en el punto F, puesto que estamos replicando el polígono de 3 lados interior, así que tan(β) = QM/MF = 1/tan(α/2).

De ahí podemos deducir que MF = QM × tan(α/2) = OQ × sin(α/2) × tan(α/2) y por tanto OF = OM + MF = OQ × cos(α/2) + OQ × sin(α/2) × tan(α/2) = OR / cos(α/2), donde en último lugar hemos sustituido OQ por OR, el radio del polígono, puesto que OR = OP = OQ.

Observe que para un polígono de 4 lados tenemos un ángulo de 90°, siendo cos(45) = 2^-1/2, con lo que OE = 2×OR×2^-1/2 = OR×2^1/2, el mismo valor que obtenemos en OF = OR / 2^-1/2 = OR×2^1/2, por lo que el punto de control exterior E coincide con el de réplica F para un polígono de 4 lados.

En resumen las distancias del centro del polígono a los puntos de control interesantes para un polígono construido con curvas cuadráticas de Bezier son los siguientes, siendo r el radio del polígono y agregando el propio centro del polígono como punto interesante, donde el ángulo α depende del número de lados del polígono α = 360° / lados:

• Centro: d₀ = 0
• Arista: d_M = r cos(α/2)
• Exterior: d_E = 2 r cos(α/2)
• Círculo: d_C = r (2-cos(α/2))
• Réplica: d_F = r / cos(α/2)

Esas distancias desde el centro del polígono a los puntos de control se pueden calcular en la herramienta independientemente de los puntos del polígono, pues sólo debemos conocer el ángulo y el radio. Pero luego la herramienta tiene que localizar las coordenadas X,Y de todos los puntos de control usando esa misma distancia sobre las coordenadas (x_o, y_o) específicas del centro del polígono, obteniéndose cada punto de control interesante de esta forma:

• p_x = x_o + d × cos(θ)
• p_y = y_o + d × sin(θ)

El ángulo θ es un múltiplo de α/2 y se obtiene a partir de cada pareja específica de puntos P,Q desde los cuales podemos obtener el punto M y a su vez el ángulo específico θ con respecto al centro O. Este es el trozo de código que lleva a cabo ese cálculo, donde (xa, ya) y (x, y) son las coordenadas de dos puntos consecutivos P,Q del polígono y que se almacenan en el array listaPuntos:

let [x, y] = [this.listaPuntos[num].x, this.listaPuntos[num].y];
let [xa, ya] = [this.listaPuntos[num-1].x, this.listaPuntos[num-1].y];
let [xm, ym] = [xa + (x-xa)/2, ya + (y-ya)/2];
let theta = Math.atan2(ym-centroY, xm-centroX);
distanciaControl = Math.abs(distanciaControl);
anguloControl = anguloControl*Math.PI/180;
if (curva==="Q") {
    let px = centroX + distanciaControl*Math.cos(theta + anguloControl);
    let py = centroY + distanciaControl*Math.sin(theta + anguloControl);
    plus = [[px, py]];
} else {
    

En el código anterior verá que forzamos la distancia de control como un valor no negativo, dado que se trata del componenente radio del vector en la dirección de la bisectriz que une el centro del polígono con el punto de control, vector que queda definido con el ángulo de control que forma con la bisectriz. En los puntos de control interesantes que hemos visto ese ángulo de control era cero, pero tiene utilidad cuando veamos las curvas cúbicas de Bezier o en el SVG generado en la Figura.

Usar la distancia de control y el ángulo de control como parámetros permite crear figuras geométricas como la de esa Figura, donde hemos utilizado un polígono de 10 lados con una distancia de control 16 y un ángulo de control de 180°. Lo que observa en esa figura es el propio SVG generado con la herramienta.

Buscando la distancia del punto control para aproximar circunferencia con Bezier cuadrática

En el apartado anterior obtuvimos el valor de la distancia d_C = r (2-cos α/2) desde el centro del polígono necesaria para ubicar el punto de control de la curva cuadrática y obtener así una aproximación a la circunferencia centrada en ese punto. Recordemos que r es el radio del polígono de n lados, siendo α = 360°/n.

Hicimos la presunción de que la distancia desde el centro de la arista (punto azul de la Figura) hasta el punto rojo sobre la circunferencia es igual a la distancia desde ese punto rojo al punto verde de control. Obtuvimos así indirectamente la distancia de control (longitud del segmento entre el origen y el punto C) y ahora vamos a intentar obtenerlo aplicando directamente la fórmula de Bezier:

donde B es el punto del arco que debe coincidir con el de la circunferencia, P es un punto del polígono y Q es el siguente, ambos separados α° y por último C es el punto de control. El parámetro t varía entre 0 y 1. Desglosando en coordenadas queda de la siguiente forma:

Para simplificar los cálculos suponemos que el polígono es de n lados genérico y se centra en el punto (0, 0) del plano. Buscaremos el punto (x_c, y_c) para obtener la distancia al punto de control con la ecuación:

Los n puntos del polígono están separados entre uno y el siguiente un ángulo α. El punto P podría ser el k-ésimo, así que expresamos las coordenadas de ese punto en función del radio y el ángulo, siendo k ∈ {0, 1, 2, ..., n-1}:

Las coordenadas del punto Q estarán a k+1 veces el ángulo:

Como la distancia buscada está sobre la bisectriz, el punto B(t) = (x(t), y(t)) está sobre la bisectriz (es el punto rojo de la Figura). Y también estará en la circunferencia de radio r y con el mismo centro (0, 0). Ese punto lo expresamos en función de la circunferencia que tendrá un ángulo de kα+α/2, agregando α/2 para llegar desde P a la bisectriz:

Simplificaremos tomando k=0, con lo que estaremos haciendo los cálculos para los dos primeros puntos del polígono. La Figura representa esa situación, con un polígono de 8 lados, donde el primer punto P con k=0 empieza sobre el eje X y el siguiente Q está a α grados de separación. Como el polígono es regular y la distancia a buscar es un escalar, el valor obtenido para esa distancia será igual en cada pareja de puntos consecutivos. Los valores anteriores quedan entonces así:

Veáse que el arco de Bezier que se aproxima a la circunferencia debe ser simétrico respecto a la bisectriz del ángulo α, por lo que el parámetro tomará el valor t = 1/2, cayendo en el centro de su recorrido. Con t = 1/2 resolvemos las fórmulas del parámetro y con los valores anteriores la fórmula de Bezier nos queda así:

Extrayendo (x_c, y_c):

Y por último obtenemos la distancia buscada:

Para resolver el último resultado he utilizado la página de cálculos matemáticos WolframAlpha usando la ecuación expresada como ((2r cos α/2 - r/2 - r/2 cos α)^2 + (2r sin α/2 - r/2 sin α)^2)^1/2 obteniendo una forma simplificada alternativa (cos(α/2) - 2) (-abs(r)) que es igual que el resultado obtenido r(2-cos α/2) dado que r>0.

Una aproximacióna a la circunferencia con cuadráticas de Bezier

En el texto anterior hemos dicho que aproximamos la curva de Bezier cuadrática a un arco de circunferencia, pues en ningún caso podemos hacerlo coincidir exactamente. Para exponer un ejemplo visual vamos a construir una circunferencia aproximándola con una Bezier cuadrática centrada en el punto (12, 12) en un polígono de 4 lados con un diámetro de 20 unidades.

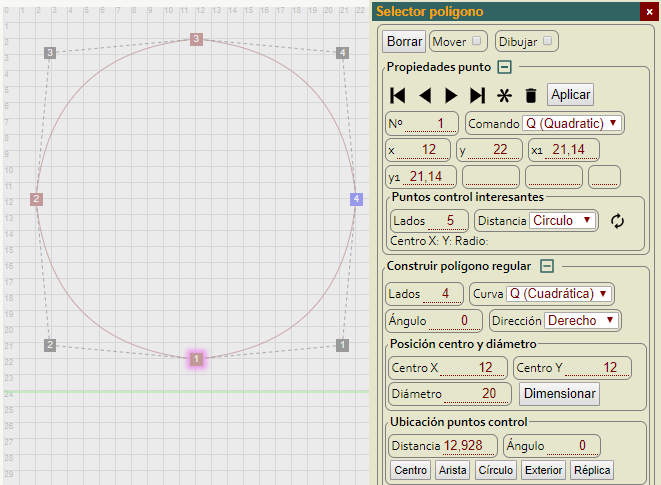
En la Figura puede ver una captura de pantalla del editor SVG. La utilidad para construir un polígono regular nos muestra el centro y diámetro. El botón "Círculo" nos calcula la distancia 12.928 desde el centro a la que deben estar los puntos de control para conseguir la mejor aproximación posible.

Tras construir el polígono con curvas de Bezier cuadráticas que unen los cuatro puntos, seleccionamos el punto 1 cuyos valores se muestran en la sección Propiedades del punto. Ese punto 1 está ubicado en (12, 22) y el punto de control de ese lado marcado con el número 1 tiene por coordenadas (21.14, 21.14). El punto anterior es el 0 (que está debajo del 4) y que está ubicado en (22, 12).

Para representar como gráfica matemática la curva de Bezier de ese cuadrante, no debemos olvidar que los ángulos en matemáticas empiezan en el primer cuadrante (superior derecha) y giran en sentido contrario a las agujas del reloj. Mientras que en HTML y CSS empiezan en el cuarto cuadrante (inferior derecha) y giran en el sentido de las agujas del reloj. Así que ese arco formado por los puntos 0 y 1 de la Figura aparecerán en el primer cuadrante en una representación matemática.

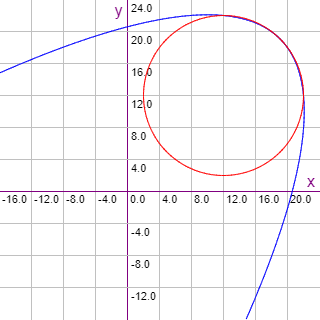
Utilizando la aplicación Gráficas matemáticas vamos a representar la curva Bezier cuadrática que une los puntos 0 y 1, tal como se muestra en la Figura en color azul. En color rojo hemos representado una circunferencia de radio 10 centrada en (12, 12).

La ecuación de Bezier particularizada para esos puntos es la siguiente:

La gráfica en color azul se produce con el parámetro en el rango t = [-3, 3]. Se trata de una parábola que intenta aproximarse al arco de circunferencia cuando el parámetro está en el rango t = [0, 1].

edita-funcion:
t=-3..3;
x = pow(1-t,2)*22 + 2*t*(1-t)*21.14 + pow(t,2)*12;
y = pow(1-t,2)*12 + 2*t*(1-t)*21.14 + pow(t,2)*22;
#
a=0..2*PI; r = 10;
x = 12 + r * cos(a);
y = 12 + r * sin(a);
_anchoxy:320_altoxy:320_zoomx:8_zoomy:8_movex:-4_movey:-4

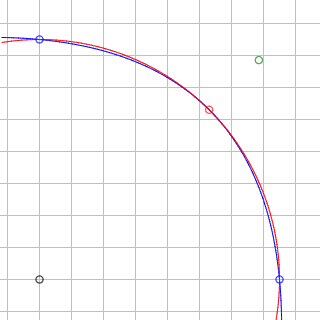
Ampliamos en la Figura la zona del arco y marcamos los puntos significativos rodeándolos con un pequeño círculo. El círculo negro es el centro del polígono en (12, 12). Se observa que hay coincidencia en los puntos del arco (círculo azules (12, 22) y (22, 12)) y en el punto rojo en la bisectriz que divide el ángulo en dos partes de 45°. El punto verde es el de control también situado sobre la bisectriz. Es evidente que los subarcos entre esos puntos se desvían significativamente del arco de circunferencia.

El polígono de 4 lados suponen arcos de 90°. Con un polígono de 3 lados los arcos serían de 360°/3 = 120° y la desviación de la Bezier cuadrática con el arco de circunferencia es mucho mayor. A medida que incrementamos el número de lados la desviacion se va reduciendo.

En la Figura puede observar un SVG con circunferencias usando elementos <path>. La primera en color rojo está construida usando el comando "A" con dos puntos, creándose una circunferencia perfecta construida con dos semiarcos de 180° cada uno. Las restantes son circunferencias aproximadas con curvas de Bezier cuadráticas en polígonos de 3 a 7 lados. Para ese tamaño vemos que con 3 o 4 lados se observa una desviación claramente visible con respecto a la circunferencia. Con 5 o más lados aparentan visualmente circunferencias. Pero no lo son.

Dado que la Figura es un SVG, puede incrementar el ZOOM de la página hasta el máximo (que suele ser 500 veces) y observar que la circunferencia con el polígono de 5 lados no es perfecta. Para comprobarlo con más precisión construiremos 4 circunferencias en SVG, todas centradas en el mismo punto y con el mismo diámetro. Una con el comando "A" en color rojo y las otras tres con el "Q" usando un polígono de 3 lados en azul, 4 lados en marrón y 5 lados en color magenta. El código que puede insertar en el editor SVG es el siguiente:

<svg viewBox="0 0 24 24" width="480" height="480">
    <path d="M2 12A10 10 0 1 0 22 12A10 10 0 1 0 2 12z" stroke="rgb(255,0,0)" fill="none" stroke-width="0.01"></path>
    <path d="M2 12Q4.5 -0.99 17 3.34Q27 12 17 20.66Q4.5 24.99 2 12z" stroke="rgb(0,0,255)" fill="none" stroke-width="0.01"></path>
    <path d="M2 12Q2.86 2.86 12 2Q21.14 2.86 22 12Q21.14 21.14 12 22Q2.86 21.14 2 12z" stroke="rgb(128,0,0)" fill="none" stroke-width="0.01"></path>
    <path d="M2 12Q2.36 5 8.91 2.49Q15.68 0.67 20.09 6.12Q23.91 12 20.09 17.88Q15.68 23.33 8.91 21.51Q2.36 19 2 12z" stroke="rgb(128,0,128)" fill="none" stroke-width="0.01"></path>
</svg>
    

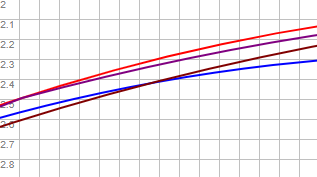
Ampliamos un trozo 1000 veces y se observa en la Figura como se desvían las cuadráticas de Bezier con respecto a la circuferencia en color rojo. Con esta ampliación apreciamos la desviación de la de color magenta construida con el polígono de 5 lados. En cualquier caso las circunferencias aproximadas con Bezier cuadráticas serán siempre interiores a la circunferencia de color rojo, coincidiendo con ella en los puntos del polígono y en el centro de las bisectrices.

En el tema siguiente veremos que se consigue mayor aproximación con una Bezier cúbica, incluso con un polígono de sólo 3 puntos.