Rectángulo único III Fila (Naked Pair)

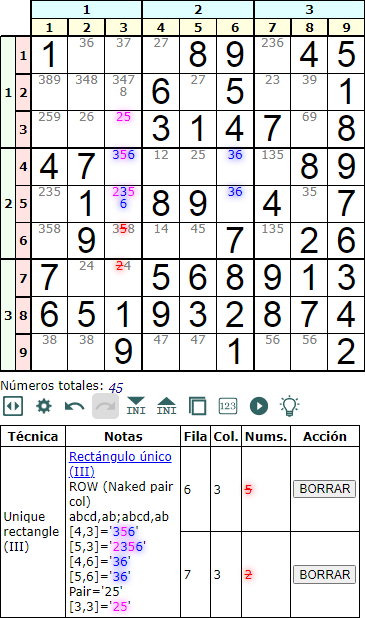
La técnica de resolución o profundizado de un Sudoku denominada rectángulo único tipo III Fila Naked Pair (unique rectangle III Row Naked Pair) del grupo de unicidad (uniqueness) se basa en un rectángulo donde dos esquinas pueden tener hasta cuatro disponibles 'abcd'.

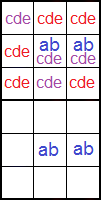
Las dos celdas con 'abcd' se ubican en dos filas de una caja, en la misma columna. Mientras que las otras dos celdas con 'ab' se ubican en las mismas filas de otra caja en la misma banda. Las celdas 'abcd' debe contener obligatoriamente 'a' y 'b'. Mientras que 'c' y 'd' deben aparecer en ambas, bien una de ellas o las dos en cada celda. En el ejemplo vemos que las celdas 'abcd' son '356' y '2356', siendo 'a' = '3', 'b' = '6', 'c' = '2' y 'd' = '5'. En la columna donde están los dos 'abcd' hemos de encontrar una única celda con los disponibles 'cd' (en color morado en el esquema). Vemos que es la celda con los disponibles '25'. En estas condiciones podemos eliminar 'c'='2' y d='5' en el resto de celdas (las señaladas en color rojo en el esquema).

Si razonamos sobre el esquema de la Figura, como 'c' y 'd' solo aparecen en las celdas 'cd' y 'abcd' pues ya se han eliminado del resto de celdas, en caso de que en 'cd' vaya 'c' entonces las dos celdas 'abcd' del rectángulo quedan 'abd'. Como 'd' no existe en otro lugar de esa columna tiene que ir necesariamente en alguna de esas dos celdas, con lo que se destruye el rectángulo de no unicidad. De igual forma se razona si en 'cd' tuviera que ir 'd'.

Si razonamos sobre el propio ejemplo, cuando en [3,3]='25' pongamos un '2' supone que [4,3]='356' y [5,3]='356', de tal forma que el '5' de estas dos celdas es único en la columna y deber ir necesariamente en alguna de las dos, deshaciendo el rectángulo de no unicidad. En cambio si en [3,3]='25' fuera un '5' supone que [4,3]='36' y [5,3]='236', con lo que el '2' de esta última celda es único en la columna y debe ir ahí necesariamente, con lo que también se deshace el rectágulo.

Se observa que la celda 'cd' = '25' junto a '2' y '5' en 'abcd' forman en cierto modo una pareja de solitarios o Naked pair. Por eso titulamos esta técnica como rectángulo único III Fila Naked Pair Columna. Es en Fila dado que 'abcd' y 'ab' aparecen en la misma fila en distintas cajas. Y es Naked Pair Columna pues la pareja de solitarios aparece en columna.

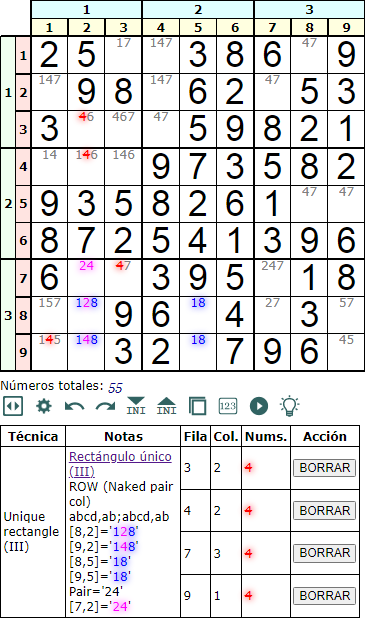
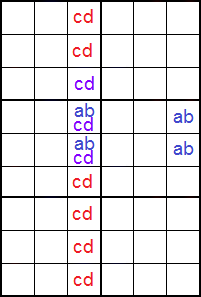
Cuando la celda con 'cd' cae dentro de la caja donde se ubican las dos celdas 'abcd', entonces podemos incrementar el número de posibilidades pues también se eliminan todos las apariciones de 'c' y 'd' dentro de la caja. En la Figura vemos que la celda con '24' está en la misma caja que las dos esquinas del rectángulo '128' y '148'.

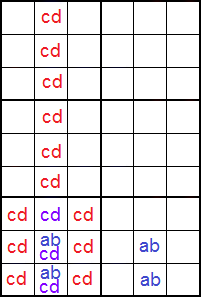
En el ejemplo si en '24' va un '2' entonces en '148' debe ir un '4' pues no existe otro '4' en la caja. De igual forma sucede si en '24' fuera un '4'. En ambos casos se deshace el rectángulo de no unicidad.

Las celdas del esquema de la Figura con disponibles 'cd' en color rojo, donde se eliminan 'c' y 'd', son las zonas de influencia al mismo tiempo de 'cd' en color morado y las dos 'abcd', que se corresponden con la caja y columna.

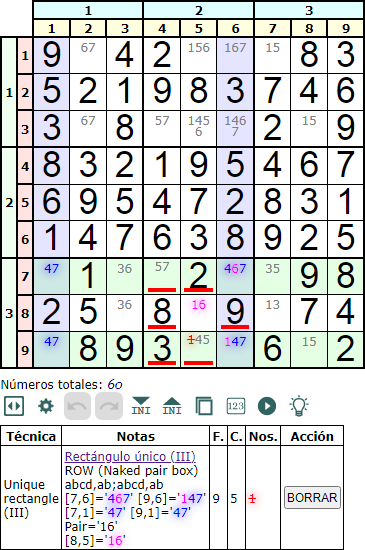
En la Figura vemos un ejemplo de un rectángulo único III en fila con un Naked pair box. La parte de la pareja '16' no se localiza en la columna 6 de influencia de las dos celdas con disponibles '467' y '147'. Pero si encontramos '16' en una celda de la misma caja y en otra columna distinta de la 6, con lo que podemos eliminar las apariciones de '1' y '6' en el resto de celdas de esa caja (las resaltadas con una línea roja inferior).

Vemos en el esquema anterior que 'cd' no se encuentra en la columna donde se ubican los 'abcd', lo que representamos como '¬cd'. Pero si lo encontramos en la misma caja. Identificando con el ejemplo tenemos 'ab'='47', 'cd'='16' y 'abcd'='4716', siendo la pareja '1' y '6' la que encontramos en la caja.

Los ejemplos anteriores responden al esquema de texto 'abcd,ab;abcd,ab'. Esto quiere decir que en dos filas encontramos 'abcd' y 'ab'. El otro esquema posible sería 'abcd,abcd;ab,ab' donde los dos 'abcd' aparecen un una fila y los dos 'ab' en otra fila. En el ejemplo de la Figura vemos '245' y '2458' en una fila, en distintas cajas. Y las dos celdas con '45' en otra fila.

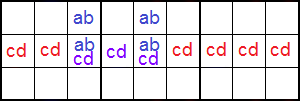
En este caso la zona de influencia de 'cd' en color morado y 'abcd' es la fila, tal como se observa en el esquema de la Figura.

Rectángulo único III Columna (Naked Pair)

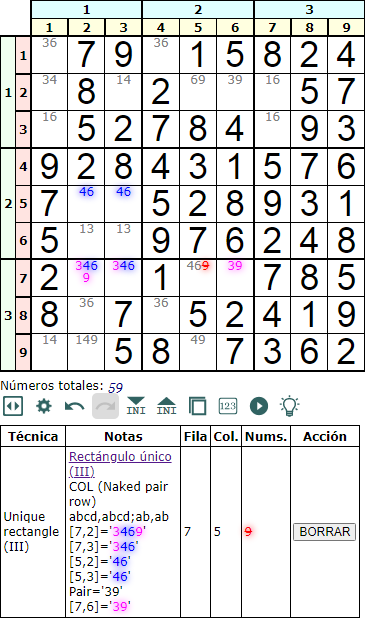
El rectángulo único III Columna (Naked Pair) es como el anterior, pero ahora las esquinas del rectángulo aparecen en una pila de cajas. En el ejemplo de la Figura vemos '3469' y '346' en una fila de una caja y en las mismas columnas de otra caja vemos las dos celdas con '46'.

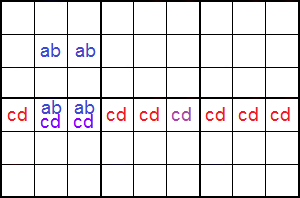
Tal como se observa en el esquema de la Figura, hemos de encontrar una única celda con los disponibles 'cd' (en color morado) en la misma fila. En estas condiciones podemos eliminar los disponibles 'c' y 'd' (en color rojo) en el resto de celdas de la fila.

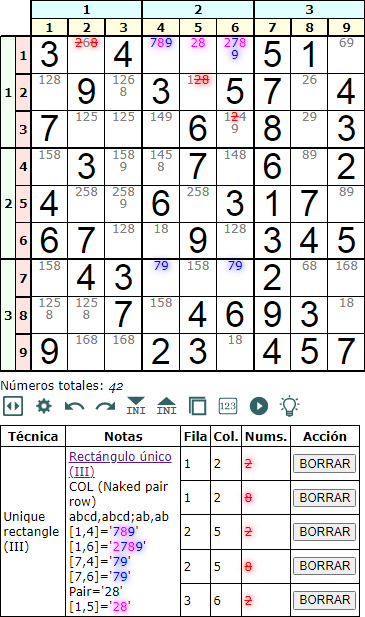
Si la celda con los disponibles 'cd' = '28' cae en la misma caja donde se ubican los dos 'abcd' ('789' y '2789'), entonces podemos eliminar los 'c' = '2' y 'd' = '8' en la fila y también en la caja.

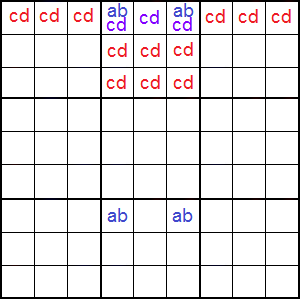
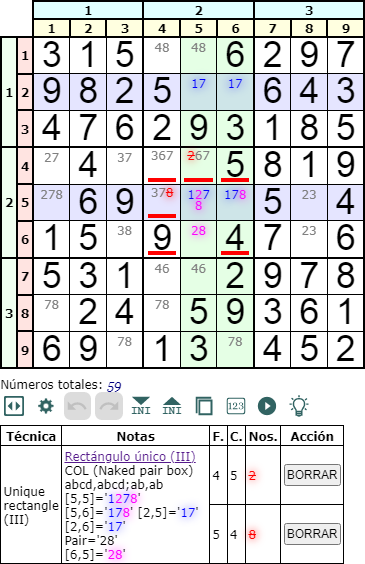
Cuando con el mismo esquema 'abcd,abcd;ab,ab' vemos que 'cd' no se encuentra en la misma fila que los 'abcd' pero si en otra celda de la misma caja, encontramos un Naked pair box como el de la Figura.

Vemos en el esquema '¬cd' indicando que 'cd' no se encuentra en la misma fila que los dos 'abcd'. Pero si se encuentra en la misma caja. En el ejemplo tenemos 'ab'='17', 'cd'='28', 'abcd'='1728'.

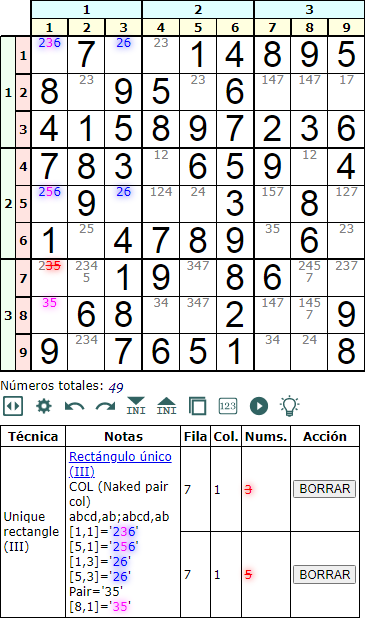
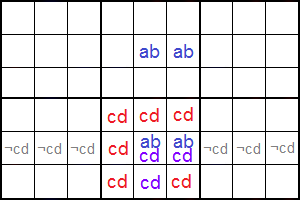
Por último cuando el esquema de texto es 'abcd,ab;abcd,ab' entonces la pareja de solitarios aparece en columna. En el ejemplo de la Figura la celda '35' forma una pareja con las dos esquinas del rectángulo '236' y '256'.

Rectángulo único III Fila (Naked Trio)

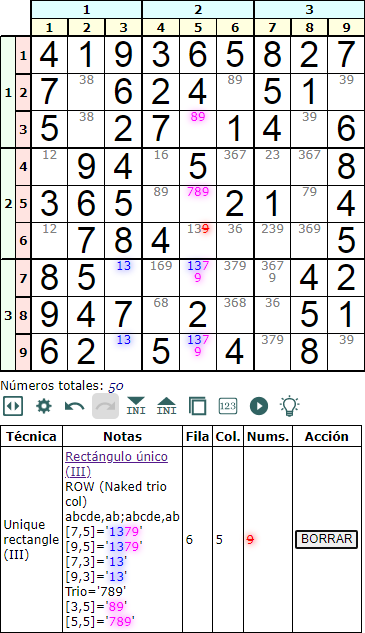
Igual que usando una pareja de solitarios podemos usar un trio de solitarios. Tenemos entonces la técnica rectángulo único III Fila (Naked Trio), unique rectangle III Row (Naked Trio). Ahora el rectángulo tiene dos esquinas con hasta cinco disponibles 'abcde'.

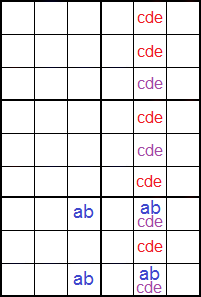
En la Figura vemos la dos esquinas del rectángulo 'abcde' con los mismos disponibles '1379' y '1379'. Las otras dos esquinas son las que tienen los disponibles '13'. Vemos que hay además dos celdas con disponibles '89' y '789'. Forman un trio solitario (naked trio) con los disponibles '7' y '9' de las dos esquinas del rectángulo en la misma columna.

Si en '89' va un '8' entonces '789' queda con '79'. Si aquí va un '7' nos quedan las dos esquinas del rectángulo con '139' por lo que el '9' debe ir en alguna de las dos pues no existe en otra celda de la columna. Si en '79' va un '9' se razonaría de igual forma. Por otro lado, si en '89' va un '9' entonces en '789' va un '8' pues sería único en la columna, mientras que las esquinas del rectángulo quedan con '137' y debe ir necesariamente un '7' en alguna de las dos, pues ya no hay más '7' en la columna. En cualquier caso se deshace el rectángulo de no unicidad.

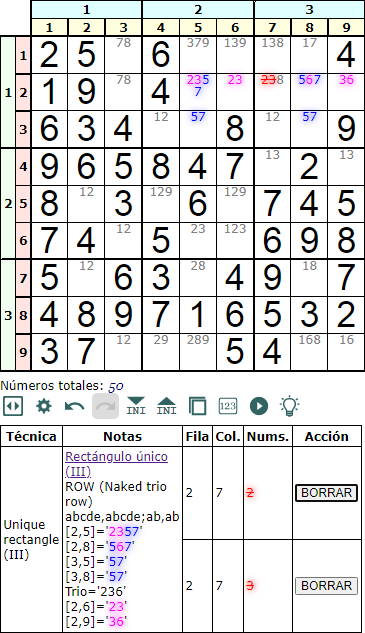
Cuando las dos esquinas 'abcde' caen en una fila, como el ejemplo de la Figura con '2357' y '567', entonces la zona de influencia es la fila. Encontramos el trio con las celdas con disponibles '23' y '36'. El trio '2', '3' y '6' se elimina del resto de celdas.

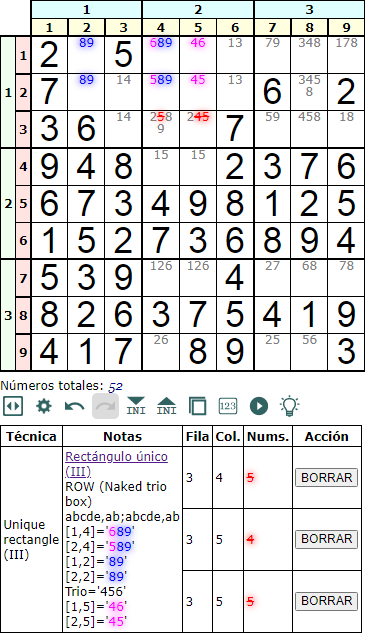
Si las dos celdas del trio con los dispoinbles 'cde' caen en la misma caja, entonces la zona de influencia de estas dos celdas y las dos esquinas 'abcde' del rectángulo es la propia caja.

En el ejemplo el trio '4', '5' y '6' se elimina en los disponibles de la caja.

Rectángulo único III Columna (Naked Trio)

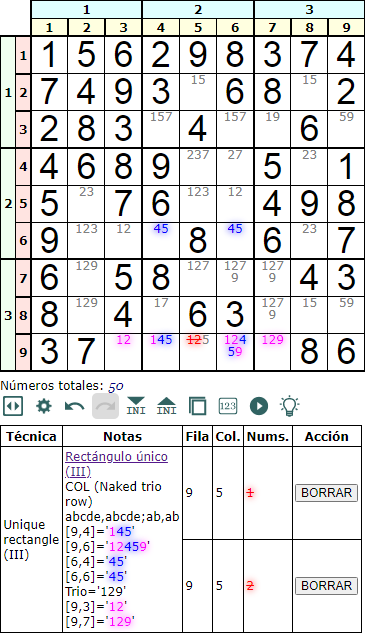
El rectángulo único III columna (unique rectangle III column) se forma con dos celdas 'abcde' en una fila de una caja y dos celdas 'ab' en otra fila de otra caja en la misma pila. En la Figura vemos un ejemplo. Hay implícito un trio de solitarios o Naked trio en la fila donde se ubican los 'abcde' con los disponibles '1', '2' y '9'.

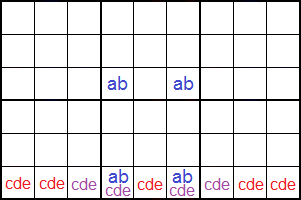
En el esquema se observa la disposición de las celdas en esa fila.

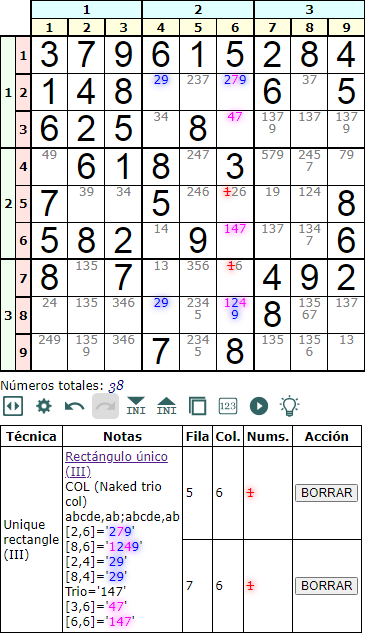
Si la ubicación de las celdas 'abcde' se encuentra en una columna como el ejemplo de la Figura, es en esa columna donde debemos encontrar el Naked trio. Vemos que se forma con los disponibles '1', '4' y '7'.

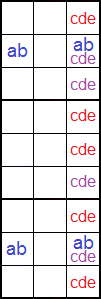
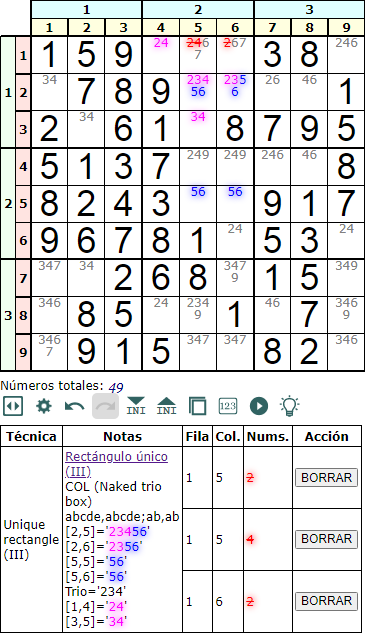
Por último cuando las dos celdas 'cde' que conforman el Naked trio se ubican en la misma caja que las dos celdas 'abcde', entonces eliminamos los disponibles 'c', 'd' y 'e' en las celdas de esa caja.