Sudoku: Unicidad. Rectángulo oculto
Rectángulo oculto tipo I Fila
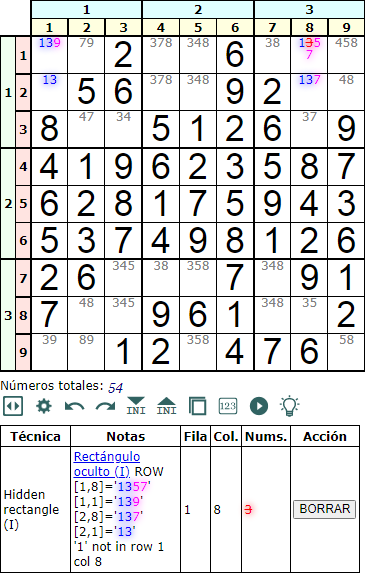
La técnica de resolución o profundizado de un Sudoku denominada rectángulo oculto tipo I en Fila (hidden rectangle type I row) del grupo unicidad (uniqueness) se basa en encontrar un rectángulo con dos esquinas opuestas en diagonal con tres o más disponibles, una esquina con dos disponibles y la última con dos o más disponibles.
En la Figura vemos un ejemplo con las dos celdas [1,1] = '139' y [2,8] = '137' en esquinas opuestas en diagonal. Las otras dos esquinas son [2,1] = '13' y [1,8] = '1357'. La pareja de disponibles '13' son las que conforman el rectángulo de no unicidad que debemos evitar a toda costa.
Las zonas de influencia de las tres esquinas '139', '1357' y '137' son la primera fila y la octava columna. Si en los disponibles de las celdas de esas zonas no encontramos alguno de los disponibles '1' o '3', podemos eliminar el otro de ellos. En el ejemplo vemos que '1' no se encuentra en esa fila 1 y columna 8, con lo que podemos eliminar '3' en la celda intersección [1,8] = '1357'.
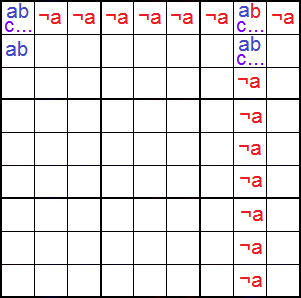
El esquema de la Figura refleja lo anterior. Con 'c...' representamos uno o más disponibles. Con '¬a' representamos que no existe 'a' en los diponibles de esa celda. En esas condiciones podemos eliminar 'b' en la celda intersección 'abc...' de la esquina superior derecha.
El objetivo es deshacer el rectángulo de no unicidad. Obviamente si no existe 'a' en la primera fila y octava columna, 'a' tiene que ir necesariamente en las celdas 'abc'. O bien va en la celda intersección y por lo tanto podemos eliminar 'b'. O si no va en esta irá en las otras dos celdas 'abc..' en diagonal, en cuyo caso también 'b' no irá en la celda intersección.
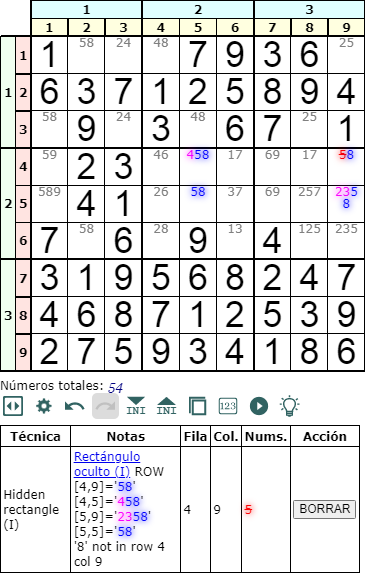
La celda intersección puede tener sólo dos disponibles. En este caso esta celda podrá ser cualquiera de las dos con dos disponibles 'ab'. En el ejemplo de la Figura vemos que es también la superior derecha del rectángulo, puesto que el '8' no existe en la fila 4 y columna 9, con lo que podemos eliminar '5' en la celda intersección.
Esta situación es muy interesante pues esa eliminación nos deja la celda intersección con un único disponible, un Naked single, lo que conducirá a tener mejores posibilidades de resolver el Sudoku.
Rectángulo oculto tipo I Columna
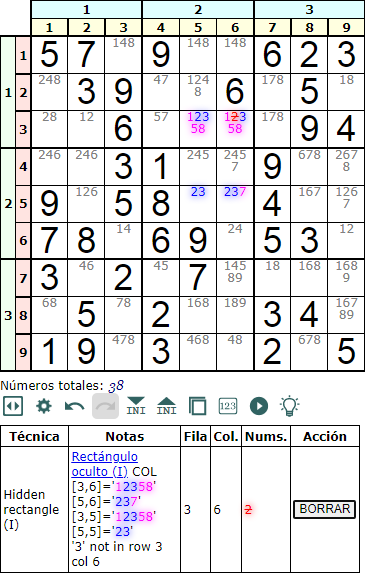
El rectángulo oculto tipo I columna (hidden rectangle type I column) funciona igual que el anterior en fila. Ahora el rectángulo se forma en una pila de cajas. En el ejemplo de la Figura vemos la celda intersección [3,6] = '12358', donde eliminamos '2' pues de la pareja '23' vemos que '3' no existe en la fila tercera ni en la columna sexta. Con esto deshacemos el rectángulo de no unicidad.
La técnica se visualiza fácilmente, por lo que no creo necesario acompañar más esquemas.
Rectángulo oculto tipo II Fila
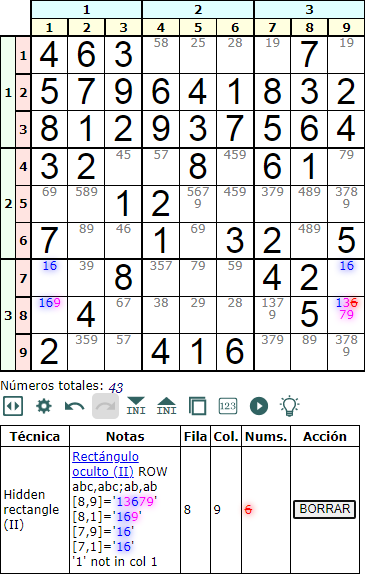
El rectángulo oculto tipo II fila (hidden rectangle type II row) se basa en dos esquemas posibles. Uno de ellos es 'abc,abc;ab,ab' donde encontraremos dos esquinas 'abc...' en una fila y las otras dos con 'ab' en la otra fila. Las celdas 'abc...' han de llevar tres o más disponibles. Y las celdas 'ab' llevarán solo dos disponibles. En el ejemplo de la Figura vemos las celdas [8,1] = '169' y [8,9] = '13679' en una fila. Mientras que [7,1] = '16' y [7,9] = '16' están en otra fila.
Vemos que '16 son los disponibles que conforman el rectángulo de no unicidad. En este caso sólo tenemos que comprobar que disponible de '16' no se encuentra en alguna de las dos columnas de influencia de las dos celdas '169' y '13679'. Vemos que '1' no se encuentra en la columna 1 de influencia de la celda '169' y si en la columna '9' de la celda '13679'. En estas condiciones podemos eliminar '6' en la celda '13679'.
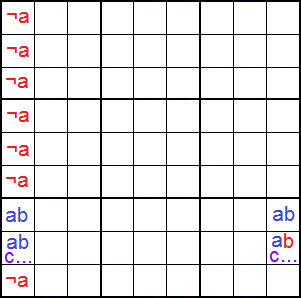
En el esquema de la Figura representamos con '¬a' el hecho de que no existe el disponible 'a' en esas celdas. Como 'a' no existe en la primera columna entonces debe ir necesariamente en alguna de las dos celdas 'ab' y 'abc...' de esa primera columna. Eliminando 'b' del 'abc...' de la última columna aseguramos que no se produce el rectángulo de no unicidad.
El otro esquema posible para el rectángulo en fila es 'abc,ab;abc,ab', encontrando las dos celdas 'abc...' en una columna y las otras dos 'ab' en otra columna de otra caja.

En el esquema vemos que si 'a' no existe en una fila podemos eliminar 'b' de la celda 'abc...' de la otra fila. El razonamiento es similar al anterior. Si 'a' no existe en la fila tendrá que ir en 'abc...' o 'ab' de esa fila. Borrando 'b' del 'abc...' de la primera columna deshacemos el rectángulo de no unicidad.
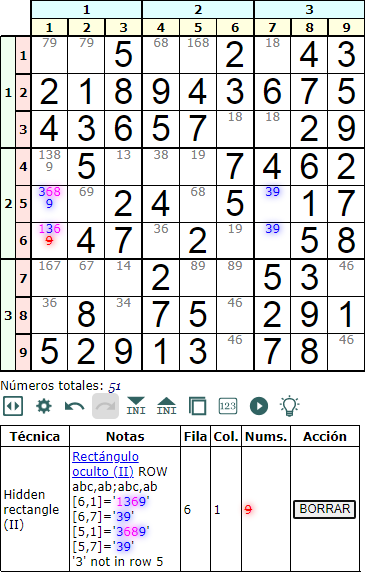
Rectángulo oculto tipo II Columna
El rectángulo oculto tipo II columna (hidden rectangle type II column) es igual que el que vimos antes para fila. El esquema 'abc,abc;ab,ab' es tal que encontramos las celdas 'abc...' en una fila y las otras dos 'ab' en otra fila de otra caja en la misma pila de cajas.
En el ejemplo de la Figura vemos dos celdas [1,4] = '1248' y [1,5] = '1248'. Y otras dos [7,4] = '48' y [7,5] = '48'. Comprobamos que '4' no existe entre los disponibles de la cuarta columna, por lo que eliminamos el '8' de la celda [1,5].
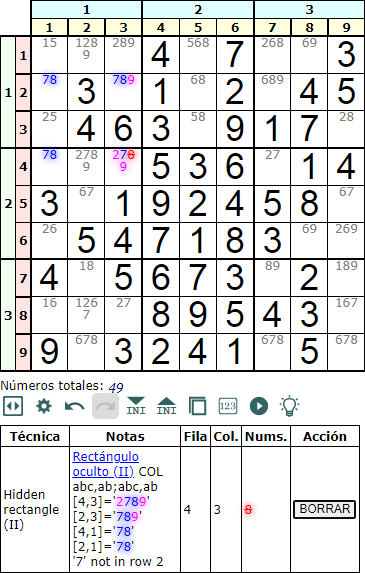
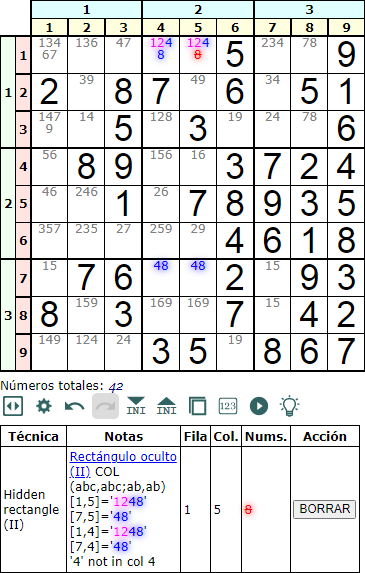
El otro esquema posible para el rectángulo oculto tipo II en columna es 'abc,ab;abc,ab'. Ahora tenemos dos celdas 'abc...' en una columna y otras dos 'ab' en otra columna.
En el ejemplo de la Figura vemos que el '7' de '78' no existe en la segunda fila, por lo que eliminamos '8' de la celda '2789' en la cuarta fila.