Único solitario (Naked single)

Las técnicas de resolución de un Sudoku son aquellas que consiguen una solución sin necesidad de utilizar el último recurso del vuelta atrás (backtracking). En estos temas también las denomino técnicas de profundizado pues nos ayudan a profundizar en el árbol de resolución.

En este tema expondré las técnicas básicas: únicos solitarios y ocultos, parejas solitarias y ocultas, trios solitarios y ocultos y bloqueados. En inglés se les denomina naked and hidden singles, naked and hidden pairs, naked and hidden trios y locked. En un siguiente tema veremos un par de técnicas del grupo Wing.

Son muchas las técnicas pero sólo dos de ellas sirven para descubrir nuevos números. Son los únicos solitarios u ocultos. Veamos en este apartado los primeros. En la Figura vemos una captura de la aplicación para la gestión de Sudokus, aplicación que nos descubre pistas para resolver el Sudoku mediante el botón con el icono . En estos temas se incluye un botón con el icono al pie de cada imagen para copiar el tablero e importarlo en esa aplicación de gestión de Sudokus.

Volviendo a la Figura, se observa que se descubre un número único solitario (naked single) en la celda [1, 6]. Como solo hay ese número disponible (o pencil mark) '6' en esa celda, entonces debe ir ahí necesariamente.

Se trata entonces de analizar los disponibles en las celdas para ver si se puede aplicar alguna técnica que pueda encontrar un nuevo número. O si esto no es posible, al menos que reduzca el número de disponibles con objeto de que en siguientes pasos si pueda obtenerse.

Único oculto (Hidden single)

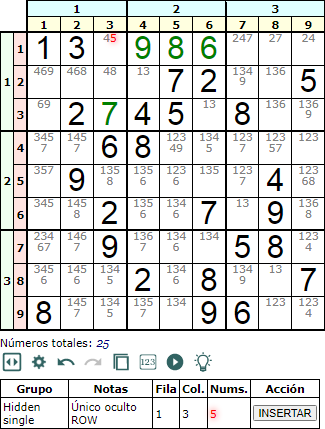
La otra técnica que descubre números son los únicos ocultos (hidden singles). En la Figura se observa que el número '5', que aparece entre los disponibles '45' de la celda [1, 3], es único en esa fila. Debe entonces ir ahí necesariamente pues no está disponible en el resto de celdas de la fila.

Vease que al mismo tiempo es único en la caja. En todas las técnicas la aplicación analiza primero las filas, luego las columnas y finalmente las cajas. Por eso aparece en este caso en la fila.

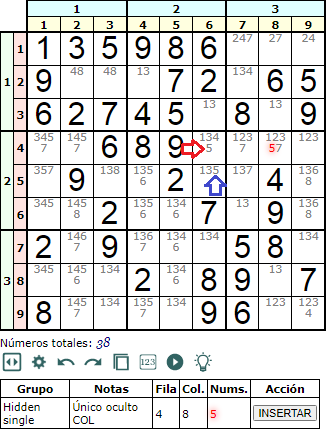
En la Figura vemos otro número '5' en la celda [4, 8] que es único oculto en esa columna, pues no hay más apariciones de ese número entre los disponibles de la octava columna.

Al insertar el '5' en la celda [4, 8] eliminaremos todos las apariciones de ese número en esa columna así como en la caja y en la fila. Vease que al eliminar el '5' señalado con una flecha en rojo hace que aparezca otro nuevo número '5' único oculto en la celda [5, 6] (flecha azul), pues ese '5' vuelve a ser único entre los disponibles de la sexta columna.

Esto evidencia que ésta y las siguiente técnicas que vamos a ver son un proceso que van reduciendo el número de disponibles dando lugar a nuevas oportunidades de ser aplicadas.

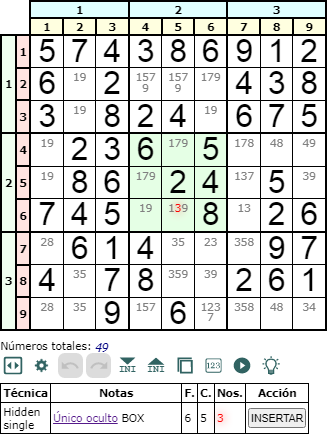
Otro esquema posible es que el número sea único en una caja, como es el número '3' en la caja central que vemos en el ejemplo de la Figura

Pareja solitarios (Naked pair)

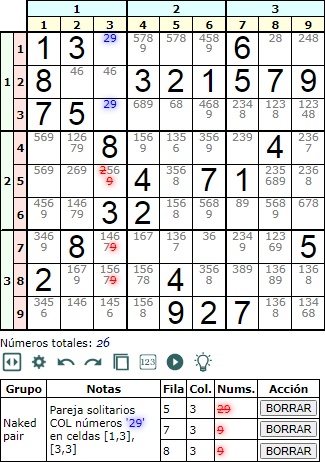
La primera y más sencilla técnica que reduce disponibles son las parejas solitarios (naked pairs). En la Figura observamos una en la tercera columna. La pareja de disponibles son los números '29' que aparecen en las dos celdas [1, 3] y [3, 3] (resaltados en azul). Vea que el '2' y el '9' también aparecen en otras celdas de esa columna (tachados y resaltados en rojo).

Si insertáramos el '2' en la celda [5, 3] entonces al eliminar su aparición en los disponibles de la columna nos encontraríamos que en las dos celdas [1, 3] y [3, 3] quedaría un '9', dando como resultado un Sudoku no completable. De igual forma pasará si insertáramos un '9' entre los resaltados en rojo, quedando entonces un '2' en esas dos celdas [1, 3] y [3, 3] llegando a una situación de no completable.

En resumen, cuando en una fila, columna o caja hay dos celdas con el mismo par de disponibles entonces podemos eliminar esos números en el resto de disponibles de esa fila, columna o caja.

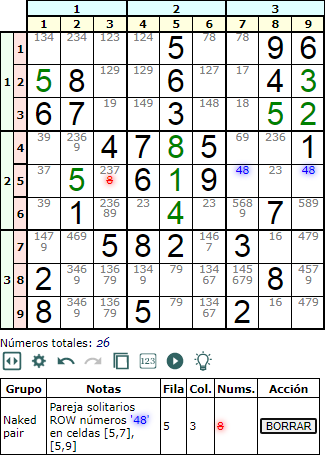
En la Figura vemos la pareja de disponibles '48' en las celdas [5, 7] y [5, 9] de la quinta fila. Es una pareja de solitarios ahora en una fila. Sólo hay una aparición de uno de sus números, el '8' en la celda [5, 3]. Al eliminar ese '8' vemos que aparece un nuevo número '8' en la celda [6, 3] como único oculto en la tercera columna (o en esa caja también).

Por eso estas técnicas, aunque sencillas, son importantes porque van descubriendo nuevas posibilidades que nos evitarán usar el último recurso del vuelta atrás.

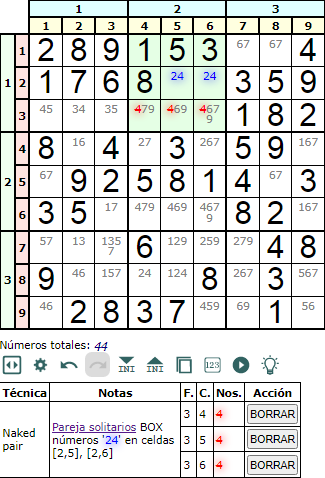
En la Figura vemos una pareja solitarios en la caja central superior, eliminando en tres celdas de esa caja el número '4'.

Pareja ocultos (Hidden pair)

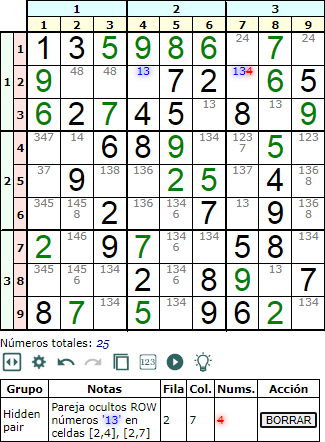
Al igual que hay únicos solitarios y únicos ocultos, también hay parejas solitarios y parejas ocultos (hidden pairs). En la Figura se observa una en la segunda fila. La pareja de disponibles '13' se localiza en las celdas [2, 4] y [2, 7]. En esta última celda además viene acompañada por un '4'. Lo importante es ver que no hay más apariciones de los números '1' y '3' en la fila, asegurando que los disponibles '13' forman una pareja en esa celdas de la fila. Así podemos eliminar el resto de disponibles de esa celda, como el '4' de la celda [2, 7].

Vease que también hay una pareja de solitarios en la misma fila con los disponibles '48' en las celdas [2, 2] y [2, 3]. Podríamos también eliminar el '4' de la celda [2, 7]. La aplicación busca primero las parejas de ocultos y luego las parejas de solitarios, razón por la cual apareció primera la vista antes con los diponibles '13' en las celdas [2, 4] y [2, 7]. En ambos casos conduciría a eliminar el mismo '4'.

En la Figura vemos una pareja de ocultos '68' en columna, donde se resalta en color verde la columna afectada. Se encuentra en el mismo tablero que el del ejemplo anterior.

En la Figura vemos una pareja ocultos en una caja, en las celdas [8, 3] y [9, 3]. Los disponibles '24' no se encuentran entre el resto de disponibles de la caja, formando una pareja. Esto conduce a que podemos eliminar el '8' entre sus disponibles.

Bloqueados (Locked)

En la técnica de bloqueados (locked) interviene una caja con una fila o columna. En la Figura puede ver un ejemplo con la primera caja y la tercera fila. La intersección de las celdas entre ambos conjuntos son las celdas [3, 1], [3, 2] y [3, 3]. Esta intersección contiene los disponibles '1' y '4' que no se encuentran en otras celdas de las fila. Mentras que '3' y '5' se encuentran en la intersección y en otras celdas de la fila, precisamente en la celda [3, 4]. En estas condiciones podemos eliminar las apariciones de '1' y '4' del resto de celdas de la caja, en este caso vemos que aparece un '14' en la celda [2, 2] a eliminar.

Para explicar lo anterior hay que pensar que los disponibles '1' y '4' en la caja están bloqueados por su disposición única en esa fila: sólo pueden ir ahí en esa fila dado que no aparecen en otras celdas de la fila exteriores a la caja. Eso asegura que se puedan eliminar en otras celdas de la caja.

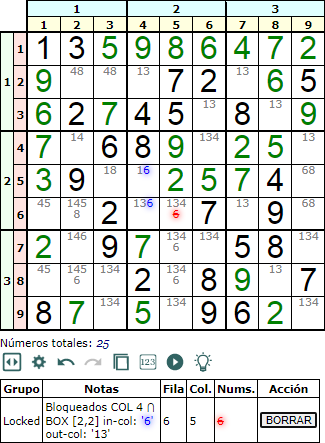
En la Figura puede ver el número '6' bloqueado en la cuarta columna en relación con la caja central. Ese '6' no aparece en la celdas de la columna exteriores a esa caja, pudiendo entonces ser eliminado en otras celdas de la caja.

Trio solitarios (Naked trio)

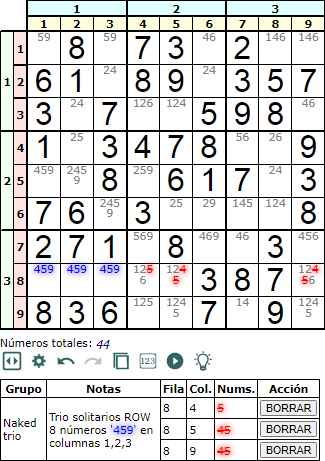
Al igual que hay parejas también podemos encontrar trios y cuartetos, aunque en la aplicación no se buscan estos últimos. En la Figura tenemos un trio solitarios (Naked trio) en la penúltima fila. Se observan resaltados en azul los disponibles '459' en las celdas [8, 1], [8, 2] y [8, 3]. Tal como razonamos para las parejas, estos tres disponibles '4', '5' y '9' han de ir necesariamente en esas celdas, pudiendo eliminar sus apariciones en el resto de celdas de la fila

Podemos razonar como el trio de números '459' en las tres celdas [8, 1], [8, 2] y [8, 3] asegura eliminar esos números del resto de celdas de la caja. Por ejemplo, si insertamos el '5' en la celda [8, 4] entonces nos quedarán los disponibles '49' en las tres celdas [8, 1], [8, 2] y [8, 3]. Esto da lugar a una situación de no completable puesto que tendríamos tres celdas y sólo dos disponibles para rellenarlas.

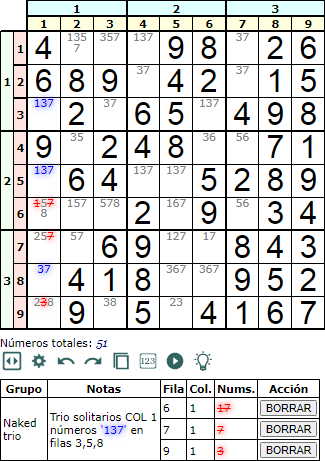
Los trios ocupan tres celdas con tres números disponibles en una fila, columna o caja. Pero no necesariamente los mismos en las tres celdas. La Figura, un Naked trio en columna, expone los disponibles '37' en la celda [8, 1] y '137' en las celdas [3, 1] y [5, 1].

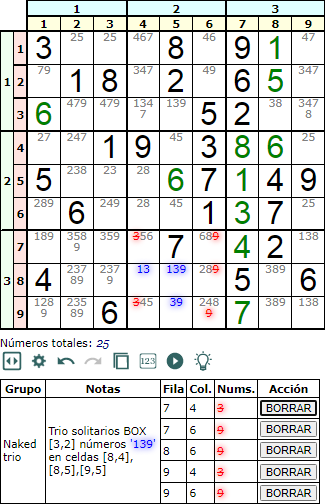
Los trios no son muy comunes y difíciles de localizar. Sin embargo suelen aportar muchas eliminaciones. En la Figura vemos un Naked trio en caja que elimina 5 disponibles en el resto de todas las celdas de esa caja.

Trio ocultos (Hidden trio)

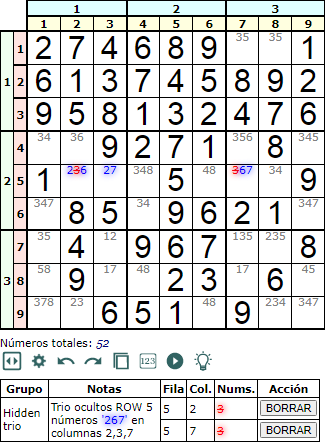
Al igual que parejas ocultos también hay trios ocultos (hidden trio). En la Figura se observan los disponibles '26', '27' y '67' en las celdas [5, 2], [5, 3] y [5, 7] respectivamente. Como dijimos antes, los trios han de relacionar tres números en tres celdas. En este caso son '2', '6' y '7' que aparecen en combinaciones de dos en las tres celdas. En los ocultos, en esta caso en fila, no deben aparecer esos '2', '6' y '7' en otras celdas de la fila, con lo que podemos eliminar sus apariciones en las celdas del trio.

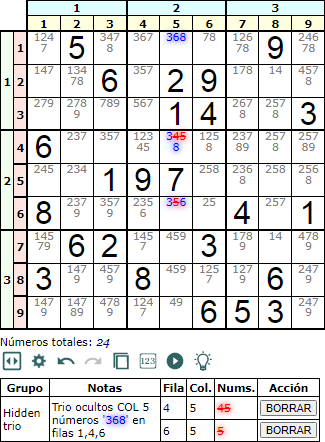
En la Figura vemos una combinación de trios en columna con los disponibles '368', '38' y '36' en las celdas [1, 5], [4, 5] y [6, 5]. Los números '3', '6' y '8' no aparecen en los disponibles del resto de celdas de esa columna, con lo que podemos eliminar el resto de disponibles en las celdas del trio.

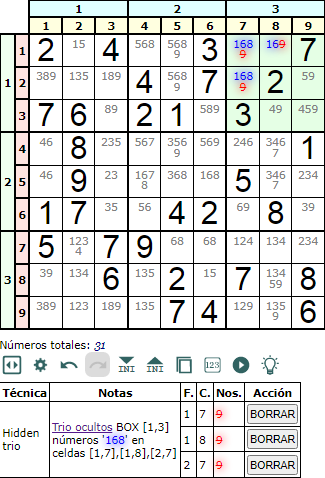
Por último vemos en la Figura un trio ocultos en la caja superior derecha. Como '1', '6' y '8' no aparecen en el resto de celdas de esa caja, podemos eliminar el '9' en las celdas afectadas.