Divide y vencerás
Algoritmos recursivos del tipo divide y vencerás
Anteriormente vimos que reducíamos por substracción el tamaño del problema en cada llamada al recursivo. ¿Qué pasaría si en lugar de substraer usamos la división? Si tenemos un problema de tamaño n iríamos reduciendo por la mitad en cada llamada. Así para llegar desde n hasta 1, si este fuera el caso trivial, se producirán los tamaños de problema sucesivos n/2, n/4, n/8, n/16, ..., 4, 2, 1. Eso son exactamente log2 n términos. Muchos menos que si vamos reduciendo de uno en uno n-1, n-2, ..., 3, 2, 1 donde hay n-1 términos. Y como log2 n < n-1 habremos reducido el coste del recursivo significativamente.
Si no nos convence veamos este ejemplo. Si tienes una tarta de manzana que mide 20cm de diámetro y la cortas por la mitad, y tomas una mitad y la vuelves a cortar por la mitad, y así sucesivamente, sólo necesitarás hacer 32 cortes para llegar a tener al final un trozo de un tamaño menor al de un átomo ¿Sólo 32 cortes?
Probablemente nos topemos con un átomo de carbono, que tiene un tamaño insignificante de 7×10-11m. Así que el número de cortes será log2(0.2 / 7×10-11) = 31.41193..., por lo que en el corte 32 tendremos un trozo con un ancho inferior a un átomo de carbono.
Si quiere comprobarlo puede copiar y pegar este código en la consola del navegador:
let cortes = 0, tarta = 0.2, atomo = 7e-11;
while (tarta > atomo){
cortes++;
tarta = tarta/2;
}
console.log(cortes); // 32
Algo parecido escribió Carl Sagan en su libro Cosmos, al inicio del capítulo IX, junto a su célebre frase Para poder hacer una tarta de manzana a partir de cero hay que inventar primero el universo.
Aunque él decía que se necesitaban 90 cortes, que no se de dónde lo deduce, en el fondo lo interesante es como con un número de divisiones que no parece muy grande podemos reducir el tamaño de una tarta de manzana hasta el de un átomo.
Si en lugar de dividir por la mitad hubiesemos elegido la estrategia de ir quitando una parte fija igual al tamaño del átomo de carbono, tendríamos que hacer 0.2 / 7×10-11 = 2.857...×109 cortes para que el último fuera igual o menor que el tamaño de un átomo de carbono. Esta estrategia de reducción por substracción es la que hemos visto en los temas anteriores. El problema se reduce en una cantidad fija en cada nueva llamada. Mientras que la de cortar por la mitad es la de reducción por división, denominada generalmente como divide y vencerás.
Si el tamaño del problema es 2.857...×109 y lo resolvemos con sólo 32 iteraciones habremos reducido enormemente el coste. Observe que ⌈ log2 2.857...×109 ⌉ = 32. Los divide y vencerás tienen un coste logarítmico, el menor de los costes típicos posibles de los algoritmos, que en orden creciente son: log(n), n, n log(n), n2, n3, 2n, n!
Raíz cuadrada entera
Si n, r son dos números enteros no negativos, diremos que raiz(n) = r cuando se cumpla r2 ≤ n < (r+1)2. Por ejemplo raiz(11) = 3 dado que 32 ≤ 11 < (3+1)2. La solución simple consistiría en iterar desde 0 a n hasta encontrar un r que cumpla r2 ≤ n < (r+1)2, como en el siguiente ejemplo:
function raiz(n){
numIter++;
let r = 0;
while (r<n){
numIter++;
r = r + 1;
if (r**2 <= n && n < (r+1)**2){
break;
}
}
return r;
}Ejemplo: Raíz cuadrada entera con un bucle
raiz(n): Math.sqrt(n)+1: Iteraciones: En el ejemplo calculamos también la raíz real usando la función de JavaScript Math.sqrt(n) para comprobar el resultado. Contamos las iteraciones del bucle, observándose que el coste exacto es T(n) = n1/2 + 1 y que T(n) ∈ O(n1/2). En esta estimación suponemos que el coste de calcular las expresiones del condicional r2 ≤ n < (r+1)2 son de coste unitario, por lo que el coste final es sólo proporcional al número de iteraciones más una iteración por las instrucciones de entrada al bucle incluyendo el while.
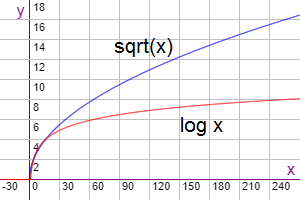
Si podemos aplicar divide y vencerás obteniendo un coste O(log(n)) reduciremos significativamente el coste de O(n1/2) que obtuvimos con el bucle anterior. En la Figura se observa que la función raíz cuadrada crece por encima del logaritmo en base 2.
Para aplicar divide y vencerás modificamos la función a raizBin(n, i=0, j=n) donde [i, j] son dos índices que indican el inicio y final del tramo donde buscar la solución. En la primera llamada será [0,n]. Si n≤1 devolveremos ese valor no produciéndose ninguna llamada. En otro caso cuando el tramo de búsqueda llegue a [i,i+1] la solucion será el valor i.
Si no fuera así, hallamos la mitad del tramo m = ⌊(i+j)/2⌋ y comprobamos lo siguiente:
- Si m2 ≤ n entonces m ≤ n1/2 y la raíz estará en el tramo derecho [m, j]
- Si m2 > n entonces m > n1/2 y la raíz estará en el tramo izquierdo [i, m]
function raizBin(n, i=0, j=n){
numIter++;
if (n<=1){
return n;
} else if (j===i+1){
return i;
} else {
let m = Math.floor((i+j)/2);
if (m**2 <= n){
i = m;
} else {
j = m;
}
return raizBin(n, i, j);
}
}Ejemplo: Raíz cuadrada entera recursiva
raizBin(n): Math.sqrt(n): Iteraciones: Coste calculado T(n): Intentaremos calcular el coste a partir del código de este divide y vencerás. Vemos que no hay bucles, por lo que todas las instrucciones en secuencia forman un coste unitario. Así que en el caso trivial el coste es uno y en el no trivial es uno más un coste de mitad de tamaño. En este recursivo n permanece constante en cada llamada y lo que varía es i y j. Pero para lo que sigue consideramos que el tamaño del problema en cada llamada es n = j-i, que viene a ser la longitud del tramo [i, j].
| T(n) = | { | 1 | si n ≤ 1 |
| T(n/2) + 1 | si n > 1 |
Restringiendo la recurrencia sólo para valores de n tal que sea un potencia de 2, es decir, n ∈ {1, 2, 4, 8, 16, ..., 2q}, entonces podemos hacer un cambio de variable n = 2q ⇒ n/2 = 2q/2 = 2q-1 con lo que podemos definir otra recurrencia S(q) = T(2q) = T(n) y que S(q-1) = T(2q-1) = T(n/2) nos queda esta definición:
| S(q) = | { | 1 | |
| S(q-1) + 1 |
Ahora si somos capaces de resolver esta recurrencia con el método de ecuación característica:
sq - sq-1 = 1 a0tn+a1tn-1+...+antn-n = bnp(n) (a0xn+a1xn-1+...+a)(x-b)d+1 = 0Identificando n=1, b=1, p(q) = q0 polinomio de grado d=0
(x1-1)(x-1)0+1 = 0 ⇒ (x-1)2 = 0Se obtiene solución r=1 de multiplicidad 2
S(q) = c1 1q + c2 q 1q = c1 + c2 qDeshacemos el cambio de variable n = 2q ⇒ q = log2 n, escribiendo en estos problemas log2 como log y recordando que definimos S(q) = T(2q) y por tanto S(log n) = T(n)
S(log n) = T(n) = c1 + c2 log nObtenemos T(n) ∈ O(log n) cuando n es una potencia 2 ¿Y qué pasa con el resto de valores?
La regla de uniformidad dice que si f(n) es una función suave y T(n) es asintóticamente no decreciente, entonces si T(n) ∈ O(f(n)) con n = bq (n potencia de b con b≥2) sucede que T(n) ∈ O(f(n)) para todo n. Las funciones suaves son como log n, n log n y cualquier polinomio P(n). No lo son 2n, n! o nlog n. Para deducirlo hemos de ver si la razón f(2n)/f(n) está o no acotada para deducir si es o no suave respectivamente. Por ejemplo para 2n tenemos la razón limn→∞ 22n/2n = limn→∞ 2n = ∞ no está acotada, mientras que para log n tenemos limn→∞ log(2n)/log(n) = limn→∞ (log 2 + log n)/log(n) = limn→∞ (1/log n) + 1 = 1 si está acotada.
Como T(n) ∈ O(log n) es asintóticamente no decreciente y f(n) = log n es suave, entonces T(n) ∈ O(log n) para todo n.
¿Y qué pasa con la solución exacta? Si obtenemos los tres primeros valores desde la recurrencia con n potencias de 2:
T(20) = T(1) = 1 T(21) = T(2) = T(2/2) + 1 = T(1) + 1 = 2 T(22) = T(4) = T(4/2) + 1 = T(2) + 1 = 3planteamos estas dos ecuaciones:
T(2) = 2 ⇒ c1 + c2 log 2 = 2 ⇒ c1 + c2 = 2 T(4) = 3 ⇒ c1 + c2 log 4 = 2 ⇒ c1 + 2 c2 = 3con soluciones c1 = 1 y c2 = 1 obteniéndose una solución exacta para n potencias de 2:
T(n) = 1 + log nEsta solución nos sirve con n ∈ {1, 2, 4, 8, 16, ..., 2q}, pero entre dos potencias de 2 no es fácil obtener una solución exacta. Si relacionamos en la siguiente tabla las iteraciones del contador numIter del ejemplo, vemos que entre dos potencias de 2 el número de iteraciones puede ser el valor de la potencia anterior o siguiente. Vemos que T(11) = T(8) = 4 o bien T(11) = T(16) = 5, lo que se verifica con numIter = 5. Y que para el siguiente T(12) = T(8) = 4 o bien T(12) = T(16) = 5, verificándose con numIter = 4.
n numIter ------------- 1 1 = 1 + log 1 2 2 = 1 + log 2 3 3 4 3 = 1 + log 4 5 3 6 4 7 4 8 4 = 1 + log 8 9 4 10 5 11 5 12 4 13 4 14 5 15 5 16 5 = 1 + log 16
Generalizamos la idea anterior para cualquier n, calculando primero log(n). Comprobamos si ⌊log(n)⌋ = ⌈log(n)⌉ en cuyo caso n será una potencia de 2 y el coste será T(n) = 1 + log(n). En otro caso T(n) = 1+⌊log(n)⌋ o bien T(n) = 1+⌈log(n)⌉. Implementamos esto en JavaScript como sigue:
let log = Math.log2(n);
let logf = Math.floor(log);
let logc = Math.ceil(log);
if (logf===logc) {
coste.textContent = 1 + log;
} else {
coste.textContent = (1+logf) + " ó " + (1+logc);
}Esto lo he podido comprobar con algunos valores, pero de ninguna forma presupone que sea cierto para todos los valores.
Búsqueda dicotómica en un Array ordenado
Este ejercicio es muy parecido al anterior de buscar la raíz cuadrada entera, donde el coste con un bucle era O(n1/2) y con un divide y vencerás era O(log n). En aquel problema se trataba de buscar la raíz cuadrada en un conjunto de puntos del segmento inicial [0, n] y ahora se trata de buscar un valor particular en ese segmento.
Si pasamos una lista ordenada como un Array con n elementos y hemos de buscar si un valor existe en esa lista usando un bucle, puede suceder que esté al inicio y el coste es unitario, que esté a la mitad y el coste es n/2 o que esté al final o que no exista en la lista y el coste es n. Hasta ahora sólo hemos puesto coste como O(n) que se lee "el coste está en el orden de...". Se entiende como orden en el peor de los casos, pues existen dos más, quedando la búsqueda en un bucle con estos tres órdenes de coste:
- En el mejor de los casos Ω(1) cuando el valor está en el inicio de la lista
- En el promedio de los casos Θ(···) según probabilidad
- En el peor de los casos O(n) cuando el valor no existe o está al final de la lista
El promedio de los casos dependerá de la distribución de probabilidad donde se encuentre el valor a buscar. Si el promedio de las veces el valor a buscar se encuentra en el último tercio del Array, podríamos decir que el coste promedio es Θ(2/3 n), pues hemos de pasar como mínimo los dos primeros tercios del bucle para entrar en el último tercio. En cualquier caso como Θ(2/3 n) ∈ Θ(n), el caso promedio también estaría en el orden de n.
No siempre vamos a conocer esa distribución de probabilidad. Pero con divide y vencerás si puede ser necesario analizar el mejor y peor de los casos, pues el siguiente recursivo se comporta peor que el bucle cuando el valor a buscar se encuentra al inicio. El recursivo busca una palabra en una lista de 200, con un coste de 8 iteraciones para buscar la primera palabra "alert". Recordando que el coste exacto era 1 + log n, vemos que este es el coste peor, puesto que 1 + log 200 = 8.6438... con valor entero inferior 8. Sin embargo tiene un coste de una iteración para buscar la palabra "onmousemove" que está en el centro de la lista.
- En el mejor de los casos Ω(1) cuando el valor está en el centro de la lista
- En el promedio de los casos Θ(···) según probabilidad
- En el peor de los casos O(log n) cuando no está en la lista y en otros casos
Por ahora sólo podemos precisar el mejor de los casos, pues el promedio dependerá de la probabilidad y el peor sabemos que es O(log n) cuando no se encuentra en la lista y en otros casos que no es fácil precisar.
El recursivo es similar al anterior. Buscamos en un segmento [i, j] buscando su centro m. Finalizamos si en esa posición está la palabra a buscar. Cuando la longitud del segmento sea menor de 2 ya no podemos dividir más y la palabra no se encuentra, devolviendo -1. En otro caso dado que la lista está ordenada comprobamos si el valor está en el segmento derecho o izquierdo, llamando nuevamente sobre uno u otro segmento. Se observa que la estructura es igual que la del recursivo de la raíz, así que el coste asintótico es T(n) ∈ O(log n) y el calculado T(n) = 1 + log n.
function buscar(lista, valor, i=0, j=lista.length){
let m = Math.floor((i+j)/2);
if (valor===lista[m]){
return m;
} else if (j===i+1) {
return -1;
} else {
if (valor>lista[m]){
i = m;
} else {
j = m;
}
return buscar(lista, valor, i, j);
}
}Ejemplo: Búsqueda dicotómica en un Array ordenado
Longitud de la lista n: buscar(lista, valor): Iteraciones: Coste calculado T(n) = 1+log(n): Exponenciación
La función exponenciación entera es f(n) = an con a, n ∈ ℕ. En JavaScript se ejecuta con Math.pow(a, n), y también con el operador doble asterisco: a**n, que es una forma simplificada de multiplicar a por si mismo n veces, que expresamos como sigue:
Esto se implementa como un bucle:
function pow(a, n){
numIter++;
if (n===0) {
return 1;
} else {
let result = a;
for (let i=1; i<n; i++){
numIter++;
result = result*a;
}
return result;
}
}Ejemplo: Exponenciación entera con bucle
pow(a, n): Math.pow(a, n): Iteraciones: La definición de la recurrencia del coste es en el caso trivial es T(0) = 1 y en el no trival T(n) = 1 + (n-1) = n. El coste es O(n) y el calculado es T(n) = n que coincide con el contador de iteraciones numIter que hemos puesto en el código. Para plasmarlo en un recursivo partimos de la recurrencia an = a×an-1 que implementamos así:
function powRec(a, n){
numIter++;
if (n===0) {
return 1;
} else {
return a * powRec(a, n-1);
}
}Ejemplo: Exponenciación entera recursiva
powRec(a, n): Math.pow(a, n): Iteraciones: La definición de la recurrencia es T(0) = 1 como antes en el caso trivial y en el no trival T(n) = 1 + T(n-1), lo que conduce a una solución general T(n) = c1 + c2 n y una particular T(n) = n+1, coincididiendo este coste calculado con el contador numIter. El asintótico sigue siendo O(n) como el del bucle.
Para aplicar divide y vencerás a este problema hemos de ver que en general an = an/2 × an/2, pero como trabajamos con entero es cierto para n par pero no para impares. Vamos a usar la división entera ⌊n/2⌋ y diferenciar entre casos pares e impares:
- Si n es par entonces n/2 = ⌊n/2⌋ ⇒ an = a⌊n/2⌋ × a⌊n/2⌋
- Si n es impar entonces n/2 = ⌊n/2⌋ + 1/2 ⇒ an = a⌊n/2⌋+1/2 × a⌊n/2⌋+1/2 de donde deducimos que an = a⌊n/2⌋ × a⌊n/2⌋ × a1
Podríamos implementarlos con el siguiente código:
function powBin(a, n){
numIter++;
if (n===0) {
return 1;
} else {
let result = powBin(a, Math.floor(n/2));
result = result*result;
if (n%2>0) result = a*result;
return result;
}
}Pero a efectos de calcular el coste en el caso de impares no podemos ignorar que la operación a1 es también una llamada al recursivo, apareciendo un caso trivial más cuando n=1. En una implementación definitiva nos ahorraríamos esto, pero a efectos de entender el problema lo vamos a contemplar con objeto de ver si podemos calcular mejor el coste exacto en el caso de impares.
function powBin(a, n){
numIter++;
if (n===0) {
return 1;
} else if (n===1) {
return a;
} else {
let result = powBin(a, Math.floor(n/2));
result = result * result;
if (n%2>0) result = result * powBin(a, 1);
return result;
}
}Ejemplo: Exponenciación entera con divide y vencerás
powBin(a, n): Math.pow(a, n): Iteraciones: Coste calculado T(n): En los casos triviales n≤1 el coste es T(n) = 1. En el caso no trivial con n par tenemos T(n) = 1 + T(n/2). Es una recurrencia como las vistas en los ejemplos anteriores, con una solución general T(n) = c1 + c2 log n de tal forma que T(n) ∈ O(log n). No debemos olvidar que la solución general se encontró para n potencias de 2, como n=2q para q ∈ ℕ. Obtuvimos T(n) = 1 + log n con n potencias de 2.
Si n es impar T(n) = 1 + T(n/2) + T(1) = T(n/2) + 2. Si resolvemos esta recurrencia para n potencias de 2 aunque n sea impar, obtenemos la misma solución general T(n) = c1 + c2 log n. Las condiciones iniciales ahora son:
T(20) = T(1) = 1 T(21) = T(2) = T(2/2) + 2 = T(1) + 2 = 3 T(22) = T(4) = T(4/2) + 2 = T(2) + 2 = 5 T(1) = c1 + c2 log 1 = 1 ⇒ c1=1 T(2) = c1 + c2 log 2 = 3 ⇒ 1 + c2 = 3 ⇒ c2 = 2 T(n) = 1 + 2 log nComo vimos en los ejemplos anteriores, por la regla de uniformidad el coste asintótico es T(n) ∈ O(log n) para cualquier valor de n. Sin embargo no parece fácil agrupar el coste calculado en una única expresión. Haremos lo mismo que en el ejemplo de la raíz obteniendo un intervalo de coste
- Si n=0 entonces T(n) = 1
- Si n es potencia de 2 entonces T(n) = 1 + ⌊log n⌋ = 1 + ⌈log n⌉ = 1 + log(n)
- En otro caso 1 + ⌈log n⌉ ≤ T(n) ≤ 1 + 2 ⌊ log n ⌋
Implementamos esto en nuestro ejemplo con el siguiente código:
if (n===0) {
coste.textContent = 1;
} else {
let log = Math.log2(n);
let logf = Math.floor(log);
let logc = Math.ceil(log);
if (logf===logc){
coste.textContent = 1+log;
} else {
coste.textContent = (1+logc) + " ≤ T(n) ≤ " + (1+2*logf);
}
}El intervalo de coste para valores que no son potencias de 2 lo he determinado de una forma experimental. No he sabido por tanto probar que es así para todo n. Veamos el coste obtenido con valores para n=8 hasta n=16 que se resume en esta tabla:
n=2q+i numIter 1+⌈log n⌉ 1+2⌊log n⌋ ------------------------------------------ 8=23+0 4 4 Es potencia 2q 9=23+1 5 5 7 10=23+2 5 5 7 11=23+3 6 5 7 12=23+4 5 5 7 13=23+5 6 5 7 14=23+6 6 5 7 15=23+7 7 5 7 16=24+0 5 5 Es potencia 2q+1
Se observa que n=8 y n=16 son dos potencias de 2 sucesivas, donde el coste es T(8) = 1 + log(8) = 4 y T(16) = 1 + log(16) = 5, lo que coincide con el número de iteraciones. En los casos intermedios que no son potencias de 2 vemos que el intervalo de coste 1 + ⌈log n⌉ ≤ T(n) ≤ 1 + 2 ⌊ log n ⌋ recoge el resto de casos donde el número de interaciones queda dentro del intervalo.
Exponenciación de matrices
Con f(n) = an definimos la exponenciación de una matriz a de dimensión 2×2 a un entero no negativo n. Es como el problema anterior, pero ahora la base es una matriz. En primer lugar necesitamos definir una función que multiplica dos matrices de 2×2:
function multiplyArrays2x2(a, b){
return [
[
a[0][0]*b[0][0] + a[0][1]*b[1][0],
a[0][0]*b[0][1] + a[0][1]*b[1][1]
],
[
a[1][0]*b[0][0] + a[1][1]*b[1][0],
a[1][0]*b[0][1] + a[1][1]*b[1][1]
]
];
}Desde un punto de vista asintótico podemos considerar que tiene un coste unitario, pues se trata de realizar en secuencia ocho multiplicaciones y cuatro sumas, todas operaciones con números que en JavaScript tiene una longitud fija (64 bits) sea cual sea el número. Con esta operación pasamos a construir el recursivo que es similar al de la exponenciación entera:
function powArray2x2Bin(a, n) {
numIter++;
if (n===0) {
return [[1, 0], [0, 1]];
} else if (n===1) {
return a;
} else {
let result = powArray2x2Bin(a, Math.floor(n/2));
result = multiplyArrays2x2(result, result);
if (n%2>0) result = multiplyArrays2x2(result, a);
return result;
}
}Ejemplo: Exponenciación de matrices
| [[, | ] |
| [, | ]] |
powArray2x2Bin(a, n):Iteraciones: El coste asintótico es T(n) ∈ O(log n). No vamos a extendernos más en costes dado que la estructura es igual que la del ejemplo anterior de la exponenciación entera. La utilidad de este ejemplo se entenderá en el siguiente apartado.
Fibonacci con coste logarítmico
En un tema anterior sobre el problema de Fibonacci partíamos de un coste O(Φn) reduciéndolo hasta uno lineal O(n), cuyo recursivo era el siguiente:
function fibonacci3(n, ri=0, rj=1){
if (n<1){
return ri;
} else if (n<2) {
return rj;
} else {
let p = n-1;
[ri, rj] = [rj, ri+rj];
return fibonacci3(p, ri, rj);
}
}Si en el ejemplo de la exponeciación de una matriz ejecutamos ([[0, 1], [1, 1]])n para los primeros valores de n obtenemos:
n an Matriz resultado -------------------------------------------- 0 a0 = [[1, 0], [0, 1]] (Matriz identidad) 1 a1 = [[0, 1], [1, 1]] 2 a2 = [[1, 1], [1, 2]] 3 a3 = [[1, 2], [2, 3]] 4 a4 = [[2, 3], [3, 5]] 5 a5 = [[3, 5], [5, 8]] 6 a6 = [[5, 8], [8, 13]]
Recordando que los primeros términos de la sucesión de Fibonacci son f(0)=0, f(1)=1, f(2)=1, f(3)=2, f(4)=3, f(5)=5, f(6)=8 vemos que podemos reconocerlos en las posiciones del Array resultado. Esto es porque partimos de una matriz [[0, 1], [1, 1]] que a medida que la vamos exponenciando va produciendo los términos de la sucesión.
Construimos una funión que declare la matriz [[0, 1], [1, 1]] y que haga una llamada a powArray2x2Bin(a, n). Obtendremos una matriz resultado del cual podemos tomar result[0][1] o result[1][0] indistintamente.
function fibonacci(n){
let a = [[0, 1], [1, 1]];
return powArray2x2Bin(a, n);
}En el ejemplo también ejecutamos fibonacci3(n), contando iteraciones en ambos.
Ejemplo: Fibonacci con coste logarítmico
fibonacci(n) con powArray2x2Bin(a, n): Iteraciones: fibonacci3(n): Iteraciones: El coste es O(log n), el mismo que el de la exponenciación de matrices. El coste calculado es T(n) = 1 + log n. Podemos reducirlo hasta T(n) = log n si tomamos el último valor de la matriz, pero siempre que no necesitemos el valor f(0) = 0 como resultado de la sucesión. Veáse por ejemplo el resalte azul en los valores obtenidos más arriba, de tal forma que para obtener f(6) = 8 haríamos powArray2x2Bin(a, 6-1) dentro de la función y así hacemos una multiplicación de matriz menos:
function fibonacci(n){
let a = [[0, 1], [1, 1]];
return powArray2x2Bin(a, n-1);
}Aunque luego en la devolución del resultado tendríamos que coger la última posición de la matriz result[1][1]. De todas formas aunque hayamos reducido el coste en una unidad, el orden sigue siendo O(log n).
Fórmula general del coste de un divide y vencerás
La aplicación de la técnica divide y vencerás en el ejemplo del apartado anterior es clarificadora de la potencia de dicha técnica. Pasar de O(n) hasta O(log n) es una reducción de iteraciones muy importante. Al igual que vimos para los problemas con reducción por substracción, en estos divide y vencerás que son del tipo reducción por división pueden identificarse con la siguiente definición de recurrencia de coste:
| T(n) = | { | c nk | si 1 ≤ n < b |
| a T(n/b) + c nk | si n ≥ b |
En esa definición a,c ∈ ℝ+, k ∈ ℝ+∪{0}, n,b ∈ ℕ, b>1, con lo que se establece la siguiente fórmula de resolución del coste de la recurrencia, que escribimos con el coste en el caso peor O() aunque se demuestra para el caso promedio Θ() también.
| T(n) = | { | O(nk) | si a < bk |
| O(nk logb n) | si a = bk | ||
| O(nlogb a) | si a > bk |
Todos los problemas que hemos visto en este tema son de la forma T(n) = T(n/2) + c n0, siendo a=1, b=2, k = 0, por lo que la solución es la del caso a = bk, solucionándose con O(nk logb n) = O(log2 n).
Y hasta aquí todo lo que he aprendido sobre recursivos que resuelven problemas reduciendo su tamaño en cada llamada. Pero los recursivos tienen también otras aplicaciones que no tienen que ver con reducir el tamaño y que veremos en los temas siguientes.