Encontrar caminos en grafos
Encontrar camino en un grafo findPath()
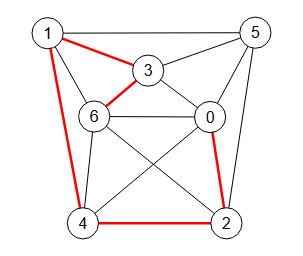
Con el algoritmo encontrar camino en un grafo entre dos nodos buscamos un camino que empiece en un nodo y acabe en el otro. En la Figura vemos el primer camino encontrado entre los nodos "0" y "6" que incluye los los nodos 0,2,4,1,3,6
En la aplicación establecemos el primer y último nodo para buscar un camino. Puede haber más de uno pero se devuelve el primero que se encuentre, a no ser que se marque encontrar todos como veremos después. Podemos modificar color camino y color texto de la arista, para los casos donde las aristas tienen una etiqueta de texto. La aplicación devuelve el resultado con una lista de nodos [0,2,4,1,3,6]. Se usa la opción inverso desmarcada pues sólo tiene efecto con la opción encontrar todos marcada, como veremos después.
Time: 0 ms Encontrar camino: [[0,2,4,1,3,6]]
Puede importar el ejemplo con este JSON:
{"nodes":[
{"index":0,"nodeOffset":"50.8 34.4","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"-47.6 0.8","parent":[{"index":-1}]},
{"index":2,"nodeOffset":"74 52","parent":[{"index":0}]},
{"index":3,"nodeOffset":"26 -9.2","parent":[{"index":0},{"index":1}]},
{"index":4,"nodeOffset":"-16.8 52","parent":[{"index":0},{"index":1},{"index":2}]},
{"index":5,"nodeOffset":"35.6 -24.4","parent":[{"index":0},{"index":1},{"index":2},{"index":3}]},
{"index":6,"nodeOffset":"-45.6 9.2","parent":[{"index":0},{"index":1},{"index":2},{"index":3},{"index":4}]}
],
"config":{
"algorithm":"Find path",
"lastIndex":6
}}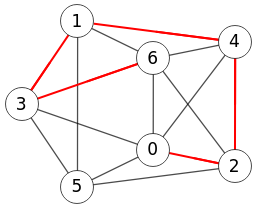
En la Figura vemos como se exporta Wolfram usando la función FindPath[g, s, t] donde "s" y "t" son el primer y último índice de nodos del camino, teniendo en cuenta que en Wolfram los índices se inician desde 1.
Usamos Table para unificarlo con el caso de que tenga que encontrar todos los caminos, aunque para este ejemplo no sería necesario. En la variable "f" tenemos el primer camino encontrado {{1,3,5,2,4,7}} como una lista de vértices. Y luego en "e" obtemos la lista de aristas {{1-3, 3-5, 5-2, 2-4, 4-7}} que necesitamos para resaltarlas en el grafo con HighlightGraph.
g = AdjacencyGraph[{{0,0,1,1,1,1,1},{0,0,0,1,1,1,1},{1,0,0,0,1,1,1},{1,1,0,0,0,1,1},{1,1,1,0,0,0,1},{1,1,1,1,0,0,0},{1,1,1,1,1,0,0}},
ImageSize->257, VertexSize->{"Scaled", 0.12}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center], 7->Placed[6,Center]}, VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindPath[g, 1, 7];
e = Table[EdgeList[PathGraph[i]], {i, f}];
h = Table[HighlightGraph[g, {Style[i, Red, Thick], Annotation[i, EdgeLabelStyle->Directive[Blue,17.5,Bold]]}], {i,e}]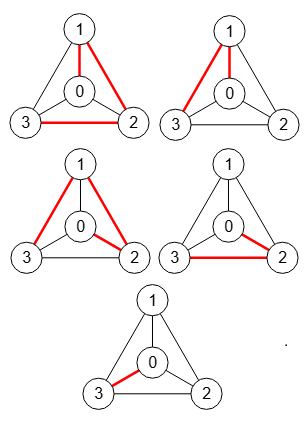
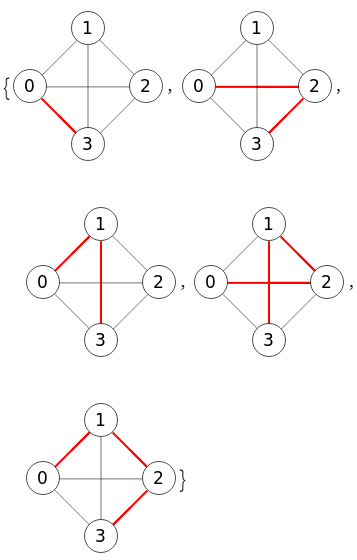
Como dijimos antes, con la opción encontrar todos nos devuelve todos los caminos entre dos nodos. En la Figura vemos todos los caminos entre los nodos "0" y "3", imagen compuesta a partir de las individuales a los que podemos acceder en la aplicación con los botones
Si hubiésemos activado también la opción inverso aparecerían los mismos caminos en orden invertido.
A continuación se muestra el resultado obtenido y el JSON para importar el ejemplo.
Time: 0 ms Encontrar camino: [[0,1,2,3],[0,1,3],[0,2,1,3],[0,2,3],[0,3]]
{"nodes":[
{"index":0,"nodeOffset":"-12.5 25","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"12.5 -25","parent":[{"index":0}]},
{"index":2,"nodeOffset":"9.15 12.5","parent":[{"index":0},{"index":1}]},
{"index":3,"nodeOffset":"-59.15 12.5","parent":[{"index":0},{"index":1},{"index":2}]}
],
"config":{
"algorithm":"Find path",
"lastIndex":3,
"findAll":true
}}
En la Figura vemos como se exportan los mismos caminos en Wolfram del ejemplo anterior. Aunque la disposición de los nodos es diferente, los caminos encontrados son los mismos.
En este caso usamos FindPath[g, 1, 4, Infinity, All], con "Infinity" busca caminos de cualquier tamaño y con "All" los busca todos. Con Table preparamos todas las listas de aristas para resaltarlas.
g = AdjacencyGraph[{{0,1,1,1},{1,0,1,1},{1,1,0,1},{1,1,1,0}}, ImageSize->156,
VertexSize->{"Scaled", 0.2}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center],
4->Placed[3,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindPath[g, 1, 4, Infinity, All];
e = Table[EdgeList[PathGraph[i]], {i, f}];
h = Table[HighlightGraph[g, {Style[i, Red, Thick], Annotation[i, EdgeLabelStyle->Directive[Blue,17.5,Bold]]}], {i,e}]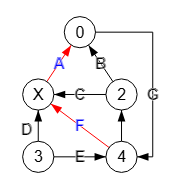
En la Figura vemos como la aplicación busca un primer camino [4,1,0] entre los nodos "4" y "0" del grafo dirigido.
Cuando uno o más nodos tienen valores diferentes de sus índices, la aplicación ofrece además el camino con los valores de los nodos [4,"X",0].
Time: 0 ms Encontrar camino: [[4,1,0]] Valores de nodos de camino ⇒ [4,"X",0]
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"value":"X","parent":[{"index":0,"value":"A"}]},
{"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"C"}]},
{"index":3,"parent":[{"index":1,"value":"D","lineTextOffset":"-0.75 0.25"},{"index":4,"value":"E"}]},
{"index":4,"parent":[{"index":1,"value":"F"},{"index":2},{"index":0,"lineOffset":"1","markerReverse":true,"value":"G"}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find path",
"firstIndex":4
}}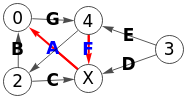
Y en la Figura vemos como se exporta a Wolfram, encontrando el mismo primer camino, aunque la disposición de los nodos es diferente.
g = AdjacencyGraph[{{0,0,0,0,1},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}}, ImageSize->188,
VertexSize->{"Scaled", 0.17}, VertexLabels->{1->Placed[0,Center], 2->Placed["X",Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], EdgeLabels->{(2->1)->"A", (3->1)->"B", (3->2)->"C", (4->2)->"D", (4->5)->"E", (5->2)->"F", (1->5)->"G"},
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindPath[g, 5, 1];
e = Table[EdgeList[PathGraph[i, DirectedEdges->True]], {i, f}];
h = Table[HighlightGraph[g, {Style[i, Red, Thick], Annotation[i, EdgeLabelStyle->Directive[Blue,17.5,Bold]]}], {i,e}]Este es el JavaScript para ejecutar findPath() que encuentre el primero o todos los caminos (con findAll verdadero). Usa getParents() para obtener los padres de un nodo y así seguir las aristas incidentes en cada nodo visitado. Está basado en la búsqueda en profundidad recursiva (getDepthFirstSearchRecursive()9.
function findPath({matrix=[], firstIndex=0, lastIndex=0, findAll=false, reverse=false, path=[], result=[]}) {
if (iter++, iter>maxIter) {
result.warning = `Maximum iterations ${maxIter} reached`;
return result;
}
try {
let n = matrix.length;
path.push(firstIndex);
if (firstIndex===lastIndex) {
result.push(path);
} else {
let parents = getParents({matrix, index:firstIndex});
if (typeof parents==="string") throw new Error(parents);
if (reverse) parents.reverse();
for (let parent of parents){
if (parent!==firstIndex && !path.includes(parent)) {
let res = findPath({matrix, firstIndex:parent, lastIndex, findAll, path:[...path], result});
if (typeof res==="string") {
result.warning = res;
return result;
}
if (!findAll && result.length>0) return result;
}
}
}
} catch(e){result = e.message}
return result;
}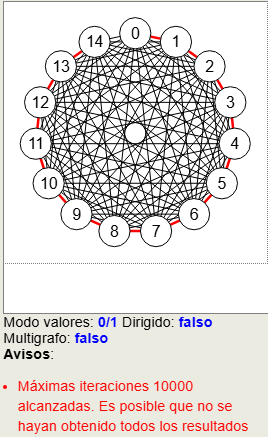
El algoritmo controla al inicio que no se superen un máximo de iteraciones maxIter que, inicialmente con valor 10000, puede también configurarse. En la Figura vemos que al tratar de encontrar todos los caminos entre los nodos "0" y "14" en un grafo completo K15 encuentra 4994 caminos y finaliza al llegar al máximo de 10000 iteraciones, adivirtiendo que Es posible que no se hayan obtenido todos los resultados
.
Según Wikipedia en un grafo completo Kn+2 hay en total ⌊ e n! ⌋ caminos distintos entre dos vértices del grafo, con lo que para este grafo K13+2 habrán en total ⌊ e 13! ⌋ = 16926797486
{"nodes":[
{"index":0,"nodeOffset":"2.5","parent":-1},
{"index":1,"nodeOffset":"62.1 -21.54","parent":0},
{"index":2,"nodeOffset":"68.9 -11.77","parent":[0,1]},
{"index":3,"nodeOffset":"70.54 2.64","parent":[0,1,2]},
{"index":4,"nodeOffset":"65.61 19.18","parent":[0,1,2,3]},
{"index":5,"nodeOffset":"53.81 35","parent":[0,1,2,3,4]},
{"index":6,"nodeOffset":"36.01 47.36","parent":[0,1,2,3,4,5]},
{"index":7,"nodeOffset":"14.15 54.13","parent":[0,1,2,3,4,5,6]},
{"index":8,"nodeOffset":"-9.15 54.13","parent":[0,1,2,3,4,5,6,7]},
{"index":9,"nodeOffset":"-31.01 47.36","parent":[0,1,2,3,4,5,6,7,8]},
{"index":10,"nodeOffset":"-48.81 35","parent":[0,1,2,3,4,5,6,7,8,9]},
{"index":11,"nodeOffset":"-60.61 19.18","parent":[0,1,2,3,4,5,6,7,8,9,10]},
{"index":12,"nodeOffset":"-65.54 2.64","parent":[0,1,2,3,4,5,6,7,8,9,10,11]},
{"index":13,"nodeOffset":"-63.9 -11.77","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12]},
{"index":14,"nodeOffset":"-57.1 -21.54","parent":[0,1,2,3,4,5,6,7,8,9,10,11,12,13]}
],
"config":{
"algorithm":"Find path",
"lastIndex":14
}}Encontrar camino de cobertura en un grafo findCoveragePath()
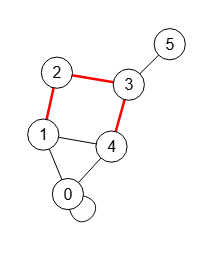
El algoritmo encontrar camino de cobertura para un subconjunto de nodos de un grafo busca un primer camino que recorra esos nodos en cualquier orden. En la Figura buscamos un camino que recorra los nodos 3,2,1,4 y el algoritmo encuentra el primer camino 1,2,3,4
Encontrar un camino de cobertura puede denominarse también como encontrar un camino Hamiltoniano parcial por el motivo que explicaremos más abajo.
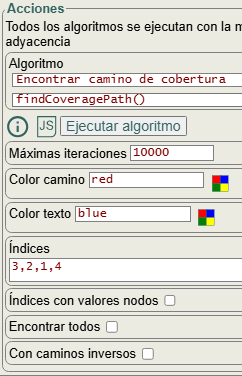
En las opciones encontramos una lista de índices de nodos que tiene que incluir todos los nodos que tiene que recorrer el camino en cualquier orden. Los índices de los nodos pueden pasarse como una lista de indices con valores de nodos, como veremos después. Así como con encontrar todos se buscarán todos los caminos posibles. También podemos modificar el color camino y color texto, para el caso de aristas etiquetadas.
La aplicación devuelve el siguiente resultado usando el siguiente JSON para importar el ejemplo.
Time: 0 ms Encontrar camino de cobertura: [[1,2,3,4]]
{"nodes":[
{"index":0,"nodeOffset":"-22.8 65.2","parent":[{"index":-1},{"index":0,"lineType":"cubic","lineOffset":"4 0 0 4"}]},
{"index":1,"nodeOffset":"-16 16.4","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-27.2 -33.4","parent":[{"index":1}]},
{"index":3,"nodeOffset":"1.6 -53.6","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-22 21.2","parent":[{"index":0},{"index":1},{"index":3}]},
{"index":5,"nodeOffset":"18 -94.8","parent":[{"index":3}]}
],
"config":{
"algorithm":"Find coverage path",
"indexes":"3,2,1,4"
}}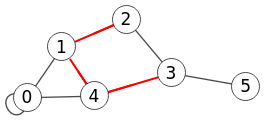
En la Figura vemos como exportamos a Wolfram ese ejemplo, encontrando otro camino 2,1,3,4, pues como veremos después son varios los caminos que cubren esos nodos. No he encontrado en Wolfram una función específica para encontrar un camino de cobertura. He tenido que recuperar todos los caminos posibles con FindPath[g, s, t, {n}, All] que busca todos los caminos ("All") con "n" nodos entre el nodo "s" y "t", iterando "s" y "t" con las combinaciones de la lista de índices "l" tomados de dos den dos (s = Subsets[l,{2}]).
Tras aplanar el resultado "r" con Flatten[r, 1] y seleccionar exactamente el que contenga los mismos nodos que la lista de índices con Select[t, ContainsExactly[#, l]&], obtenemos todas las listas de aristas y resaltamos con HighlightGraph.
Con la última sentencia If[False, h, First[h]] si buscamos todos los caminos pasaremos "True" y "False" en otro caso, presentándose todos o sólo el primero que encuentre como es el caso de este ejemplo.
g = AdjacencyGraph[{{1,1,0,0,1,0},{1,0,1,0,1,0},{0,1,0,1,0,0},{0,0,1,0,1,1},{1,1,0,1,0,0},{0,0,0,1,0,0}},
ImageSize->266, VertexSize->{"Scaled", 0.12}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center]}, VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
l = {4,3,2,5};
n = Length[l]-1;
s = Subsets[l,{2}];
r = Table[FindPath[g, Part[i,1], Part[i, 2], {n}, All], {i, s}];
t = Flatten[r, 1];
f = Select[t, ContainsExactly[#, l]&];
e = Table[EdgeList[PathGraph[i]], {i, f}];
h = Table[HighlightGraph[g, {Style[i, Red, Thick], Annotation[i, EdgeLabelStyle->Directive[Blue,17.5,Bold]]}], {i,e}];
If[False, h, First[h]]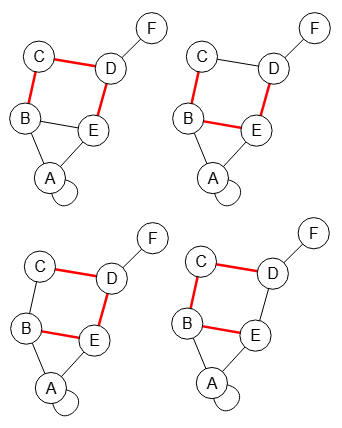
Para ejecutar el mismo ejemplo pero con la opción encontrar todos marcada, modificamos el grafo dándole valores alfabético mayúsculas a los nodos, lo que conseguimos con la propiedad "nodeValueAuto":"alphabetic-upper" que pasamos en la configuración del JSON.
Podemos pasar la misma lista de índices 3,2,1,4 o una lista de índices con valores nodos marcando esa opción, pasando los valores D,C,B,E que se corresponden con esos índices.

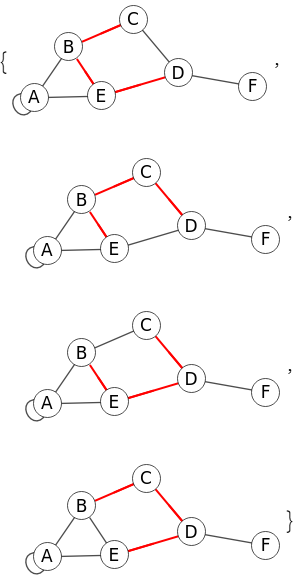
Obtenemos el resultado siguiente con 4 caminos, tanto en listas de índices como en listas de valores, grafos resaltados a los que podemos acceder con los botones Componemos en una sóla imagen los 4 grafos resaltados que vemos en la Figura.
Time: 0 ms Encontrar camino de cobertura: [[1,2,3,4],[2,1,4,3],[1,4,3,2],[4,1,2,3]] Valores de nodos de camino ⇒ ["B","C","D","E"], ["C","B","E","D"], ["B","E","D","C"], ["E","B","C","D"]
{"nodes":[
{"index":0,"nodeOffset":"-22.8 65.2","parent":[{"index":-1},{"index":0,"lineType":"cubic","lineOffset":"4 0 0 4"}]},
{"index":1,"nodeOffset":"-16 16.4","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-27.2 -33.4","parent":[{"index":1}]},
{"index":3,"nodeOffset":"1.6 -53.6","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-22 21.2","parent":[{"index":0},{"index":1},{"index":3}]},
{"index":5,"nodeOffset":"18 -94.8","parent":[{"index":3}]}
],
"config":{
"nodeValueAuto":"alphabetic-upper",
"algorithm":"Find coverage path",
"indexes":"D,C,B,E",
"indexesWithNodeValues":true,
"findAll":true
}}
En la Figura vemos el resultado en Wolfram de encontrar todos los caminos de cobertura para los nodos con índices 3,2,1,4.
El código es el mismo que vimos antes para el primer camino, sólo cambia la última sentencia If[True, h, First[h]], que ahora pone "True" para devolver todos los caminos.
g = AdjacencyGraph[{{1,1,0,0,1,0},{1,0,1,0,1,0},{0,1,0,1,0,0},{0,0,1,0,1,1},{1,1,0,1,0,0},{0,0,0,1,0,0}},
ImageSize->266, VertexSize->{"Scaled", 0.12}, VertexLabels->{1->Placed["A",Center], 2->Placed["B",Center], 3->Placed["C",Center],
4->Placed["D",Center], 5->Placed["E",Center], 6->Placed["F",Center]}, VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
l = {4,3,2,5};
n = Length[l]-1;
s = Subsets[l,{2}];
r = Table[FindPath[g, Part[i,1], Part[i, 2], {n}, All], {i, s}];
t = Flatten[r, 1];
f = Select[t, ContainsExactly[#, l]&];
e = Table[EdgeList[PathGraph[i]], {i, f}];
h = Table[HighlightGraph[g, {Style[i, Red, Thick], Annotation[i, EdgeLabelStyle->Directive[Blue,17.5,Bold]]}], {i,e}];
If[True, h, First[h]]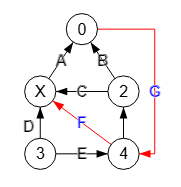
En la Figura vemos el primer camino de cobertura encontrado en un grafo dirigido que cubra los nodos 0,1,4, donde el nodo "1" se etiqueta con "X".
Time: 0 ms Encontrar camino de cobertura: [[0,4,1]] Valores de nodos de camino ⇒ [0,4,"X"]
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"value":"X","parent":[{"index":0,"value":"A"}]},
{"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"C"}]},
{"index":3,"parent":[{"index":1,"value":"D","lineTextOffset":"-0.75 0.25"},{"index":4,"value":"E"}]},
{"index":4,"parent":[{"index":1,"value":"F"},{"index":2},{"index":0,"lineOffset":"1","markerReverse":true,"value":"G"}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find coverage path",
"indexes":"0,1,4"
}}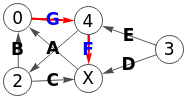
En la Figura vemos el resultado en Wolfram de un camino de cobertura para los nodos 0,1,4, que en Wolfram hay que agregar uno siendo 1,2,5.
El código es el mismo que vimos antes, solo cambia PathGraph[i, DirectedEdges->True] agregando lo necesario para especificar que las aristas son de un grafo dirigido.
g = AdjacencyGraph[{{0,0,0,0,1},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}}, ImageSize->188,
VertexSize->{"Scaled", 0.17}, VertexLabels->{1->Placed[0,Center], 2->Placed["X",Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(2->1)->"A", (3->1)->"B", (3->2)->"C", (4->2)->"D", (4->5)->"E", (5->2)->"F", (1->5)->"G"},
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
l = {1,2,5};
n = Length[l]-1;
s = Subsets[l,{2}];
r = Table[FindPath[g, Part[i,1], Part[i, 2], {n}, All], {i, s}];
t = Flatten[r, 1];
f = Select[t, ContainsExactly[#, l]&];
e = Table[EdgeList[PathGraph[i, DirectedEdges->True]], {i, f}];
h = Table[HighlightGraph[g, {Style[i, Red, Thick], Annotation[i, EdgeLabelStyle->Directive[Blue,17.5,Bold]]}], {i,e}];
If[False, h, First[h]]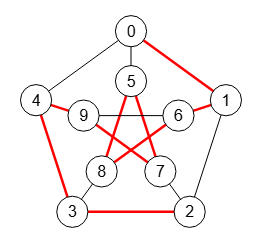
Encontrar un camino de cobertura para todos los nodos de un grafo con la función que estamos viendo getFindCoveragePath() equivale a encontrar un camino Hamiltoniano con la función findHamiltonianPath() que veremos en el tema siguiente, pues un camino Hamiltoniano es aquel que recorre todos los nodos del grafo. En la Figura vemos un camino encontrado 0,1,6,8,5,7,9,4,3,2 que es el mismo que uno de los caminos Hamiltonianos entre los nodos "0" y "2".
Debido a lo anterior el algoritmo encontrar camino de cobertura para un subconjunto de nodos de un grafo podría denominarse encontrar un camino Hamiltoniano parcial.
Este es el resultado del camino de cobertura que cubre todos los nodos usando el siguiente JSON. Observe que pasamos todos los índices del grafo 0,1,2,3,4,5,6,7,8,9 y además marcamos encontrar todos, obteniéndos muchos resultados que hemos abreviado, resaltando uno de ellos 0,1,6,8,5,7,9,4,3,2
Time: 12 ms Encontrar camino de cobertura: [[0,1,2,3,4,9,6,8,5,7],[0,1,2,3,4,9,7,5,8,6],[0,1,2,7,5,8,3,4,9,6], [0,1,2,7,5,8,6,9,4,3],[0,1,6,8,5,7,2,3,4,9],[0,1,6,8,5,7,9,4,3,2], ··· [9,6,8,3,4,0,5,7,2,1],[9,6,8,5,7,2,1,0,4,3],[9,6,8,5,7,2,3,4,0,1]]
{"nodes":[
{"index":0,"nodeOffset":"2.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"65.54 2.64","parent":[{"index":0}]},
{"index":2,"nodeOffset":"51.01 22.36","parent":[{"index":1}]},
{"index":3,"nodeOffset":"-4.34 -2.64","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-35.54 2.64","parent":[{"index":0},{"index":3}]},
{"index":5,"nodeOffset":"-22.5 -5","parent":[{"index":0}]},
{"index":6,"nodeOffset":"21.52 -16.18","parent":[{"index":1}]},
{"index":7,"nodeOffset":"-2.41 -18.82","parent":[{"index":2},{"index":5}]},
{"index":8,"nodeOffset":"-9.26 -43.82","parent":[{"index":3},{"index":5},{"index":6}]},
{"index":9,"nodeOffset":"-41.52 -16.18","parent":[{"index":4},{"index":6},{"index":7}]}
],
"config":{
"algorithm":"Find coverage path",
"indexes":"0,1,2,3,4,5,6,7,8,9",
"findAll":true
}}Ejecutando el camino Hamiltoniano findHamiltonianPath() entre los nodos "0" y "2" obtenemos este resultado con el JSON siguiente, obteniendose el mismo camino 0,1,6,8,5,7,9,4,3,2
Time: 0 ms Encontrar camino Hamiltoniano: [[0,1,6,8,5,7,9,4,3,2]]
{"nodes":[
{"index":0,"nodeOffset":"2.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"65.54 2.64","parent":[{"index":0}]},
{"index":2,"nodeOffset":"51.01 22.36","parent":[{"index":1}]},
{"index":3,"nodeOffset":"-4.34 -2.64","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-35.54 2.64","parent":[{"index":0},{"index":3}]},
{"index":5,"nodeOffset":"-22.5 -5","parent":[{"index":0}]},
{"index":6,"nodeOffset":"21.52 -16.18","parent":[{"index":1}]},
{"index":7,"nodeOffset":"-2.41 -18.82","parent":[{"index":2},{"index":5}]},
{"index":8,"nodeOffset":"-9.26 -43.82","parent":[{"index":3},{"index":5},{"index":6}]},
{"index":9,"nodeOffset":"-41.52 -16.18","parent":[{"index":4},{"index":6},{"index":7}]}
],
"config":{
"algorithm":"Find Hamiltonian path",
"lastIndex":2
}}A continuación presentamos un código JavaScript para ejecutar una versión poco eficiente de findCoveragePath() usando findPath() que vimos en el apartado anterior y la función combinatoria combine(list, k) para generar la combinaciones de una lista de elementos. Se basa en generar todas las combinaciones de los vértices que queremos cubrir en combinaciones de parejas de vértices, con objeto de encontrar todos los caminos posibles con findPath() entre esa pareja de vértices y ver cuál de ellos contiene los mismos vértices que los que tenemos que cubrir.
Esto funciona cuando el número de caminos posibles entre dos nodos no es muy alto. Pero como explicamos más arriba, en un grafo completo con 15 nodos hay 16926797486 caminos posibles, con lo que el algoritmo no podrá finalizar devolviéndolos todos.
//Inefficient algorithm for demonstration purposes only, use findCoveragePath() instead.
//Not included in the application.
function findCoveragePathCombine({matrix=[], indexes=[], findAll=true}){
let result = [];
result.warnings = [];
try {
if (indexes.length>1) {
if ((new Set(indexes)).size!==indexes.length) {
throw new Error(`Indexes has repeated elements`);
}
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
let combinations = combine(indexes, 2);
if (typeof combinations==="string") throw new Error(combinations);
if (combinations.hasOwnProperty("warning")) {
result.warnings.push(combinations.warning);
}
let pairs = [];
for (let pair of combinations) {
pairs.push(pair);
if (directed) pairs.push(pair.toReversed());
}
for (let [firstIndex, lastIndex] of pairs.values()){
let paths = findPath({matrix, firstIndex, lastIndex, findAll:true});
if (typeof paths==="string") throw new Error(paths);
if (paths.warning) throw new Error(paths.warning);
for (let path of paths) {
if (path.length===indexes.length && path.every(v => indexes.includes(v))) {
result.push(path);
if (!findAll) return result;
}
}
}
}
} catch(e){result.warnings.push(e.message)}
return result;
}Así que he tenido que buscar otra forma más eficiente de ejecutar findCoveragePath() que se expone a continuación, usando isGraphDirected para saber si el grafo es dirigido y getEdges() para obtener las aristas del grafo. Se basa en iterar de forma recursiva por esas aristas comprobando cuáles forman un camino que incluya todos los vértices que queremos cubrir.
function findCoveragePath({matrix=[], indexes=[], findAll=true, withReversePaths=false}){
let result = [];
result.warnings = [];
try {
if (indexes.length>1) {
if ((new Set(indexes)).size!==indexes.length) {
throw new Error(`Indexes has repeated elements`);
}
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
let edgesAll = getEdges({matrix, edgesCompact:false});
if (typeof edgesAll==="string") throw new Error(edgesAll);
let edges = Object.keys(edgesAll).map(v => v.split(",").map(v => +v)).
filter(v => indexes.includes(v[0]) && indexes.includes(v[1]));
function rec(edges=[], indexes=[], findAll=false, withReversePaths,
directed=false, path=[]) {
let result = [];
result.warning = "";
try {
if (iter++, iter>maxIter) {
if (path.length===indexes.length) {
result.push([path[0][0], ...path.map(v => v[1])]);
}
throw new Error(`Maximum iterations ${maxIter} reached`);
}
if (path.length===0) {
for (let i=0; i<edges.length; i++) {
let edge = edges[i];
let edges2 = edges.toSpliced(i, 1);
let res = rec(edges2, indexes, findAll, withReversePaths,
directed, [edge]);
if (typeof res==="string") throw new Error(res);
if (res.warning!=="") result.warning = res.warning;
if (res.length>0) {
if (directed || withReversePaths) {
result.push(...res);
} else {
let r = res[0].toReversed().join(",")
if (!result.some(v => v.join(",")===r)) {
result.push(...res);
}
}
if (!findAll) break;
}
}
} else {
let vertexsPath = [path[0][0], ...path.map(v => v[1])];
if (indexes.every(v => vertexsPath.includes(v))) {
result.push(vertexsPath);
} else {
let target = path[path.length-1];
let vertexs = path.map(v => v[0]);
for (let i=0; i<edges.length; i++) {
let edge = edges[i];
if (target[0]!==edge[1] && target[1]===edge[0] &&
!vertexs.includes(edge[0])) {
let path2 = [...path, [...edge]];
let edges2 = edges.toSpliced(i, 1);
let res = rec(edges2, indexes, findAll,
withReversePaths, directed, path2);
if (typeof res==="string") throw new Error(res);
if (res.warning!=="") result.warning = res.warning;
if (res.length>0) {
result.push(...res);
if (!findAll) break;
}
}
}
}
}
} catch(e) {result.warning = e.message}
return result;
}
let res = rec(edges, indexes, findAll, withReversePaths, directed);
if (res.warning!=="") result.warnings.push(res.warning);
result = res;
}
} catch(e){result.warnings.push(e.message)}
return result;
}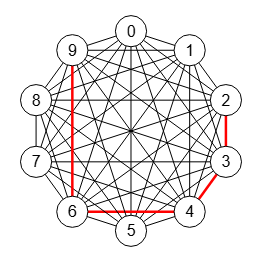
En la Figura vemos que usando el algoritmo findCoveragePath con menos de 10000 iteraciones en el recursivo (sólo se necesitan 8 iteraciones y un tiempo ejecución inferior a 1 ms) es suficiente para encontrar un primer camino que cubra los vértices 9,2,3,4,6 en un grafo completo K10, devolviendo el camino [2,3,4,6,9]. Pero con findCoveragePathCombine() necesitaremos 219217 iteraciones (tiempo ejecución en torno a 125 ms). Para grafos con más caminos como el K15 que dijimos antes esa búsqueda es infructuosa con ese algoritmo.
{"nodes":[
{"index":0,"nodeOffset":"2.5","parent":-1},
{"index":1,"nodeOffset":"66.01 -17.36","parent":0},
{"index":2,"nodeOffset":"70.54 2.64","parent":[0,1]},
{"index":3,"nodeOffset":"60.54 27.36","parent":[0,1,2]},
{"index":4,"nodeOffset":"36.01 47.36","parent":[0,1,2,3]},
{"index":5,"nodeOffset":"2.5 55","parent":[0,1,2,3,4]},
{"index":6,"nodeOffset":"-31.01 47.36","parent":[0,1,2,3,4,5]},
{"index":7,"nodeOffset":"-55.54 27.36","parent":[0,1,2,3,4,5,6]},
{"index":8,"nodeOffset":"-65.54 2.64","parent":[0,1,2,3,4,5,6,7]},
{"index":9,"nodeOffset":"-61.01 -17.36","parent":[0,1,2,3,4,5,6,7,8]}
],
"config":{
"algorithm":"Find coverage path",
"indexes":"9,2,3,4,6"
}}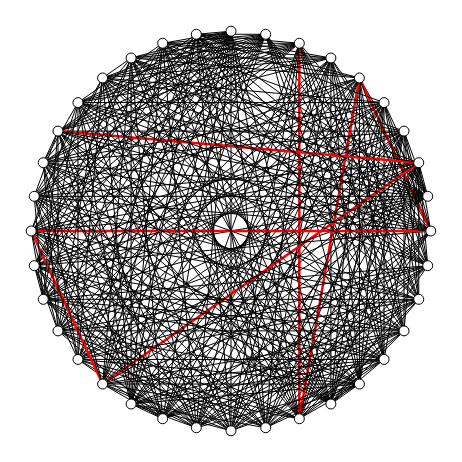
En la Figura vemos como encontrar un camino de cobertura de los vértices 9,16,2,27,30,7,4,22 en un grafo Kneser 9,2 que tiene 36 nodos y 378 aristas y una cantidad de caminos entre dos nodos que no soy capaz de calcular. Encuentra un primer camino [2,16,4,9,27,22,7,30] que cubre esos nodos con menos de 10000 iteraciones y un tiempo de ejecución de 1ms.
{"nodes":[
{"index":0,"nodeOffset":"81.39","parent":-1},
{"index":1,"nodeOffset":"84.17 1.22","parent":-1},
{"index":2,"nodeOffset":"86.53 4.82","parent":-1},
{"index":3,"nodeOffset":"88.06 10.72","parent":-1},
{"index":4,"nodeOffset":"88.36 18.72","parent":-1},
{"index":5,"nodeOffset":"87.11 28.58","parent":-1},
{"index":6,"nodeOffset":"84 40","parent":-1},
{"index":7,"nodeOffset":"78.79 52.64","parent":-1},
{"index":8,"nodeOffset":"167.83 41.11","parent":[2,3,4,5,6,7]},
{"index":9,"nodeOffset":"165.6 55","parent":[1,3,4,5,6,7]},
{"index":10,"nodeOffset":"160.94 68.89","parent":[1,2,4,5,6,7]},
{"index":11,"nodeOffset":"153.89 82.36","parent":[1,2,3,5,6,7]},
{"index":12,"nodeOffset":"144.54 95","parent":[1,2,3,4,6,7]},
{"index":13,"nodeOffset":"133.09 106.42","parent":[1,2,3,4,5,7]},
{"index":14,"nodeOffset":"119.78 116.28","parent":[1,2,3,4,5,6]},
{"index":15,"nodeOffset":"104.91 124.28","parent":[0,3,4,5,6,7,10,11,12,13,14]},
{"index":16,"nodeOffset":"88.83 130.18","parent":[0,2,4,5,6,7,9,11,12,13,14]},
{"index":17,"nodeOffset":"71.91 133.78","parent":[0,2,3,5,6,7,9,10,12,13,14]},
{"index":18,"nodeOffset":"54.57 135","parent":[0,2,3,4,6,7,9,10,11,13,14]},
{"index":19,"nodeOffset":"37.23 133.78","parent":[0,2,3,4,5,7,9,10,11,12,14]},
{"index":20,"nodeOffset":"20.31 130.18","parent":[0,2,3,4,5,6,9,10,11,12,13]},
{"index":21,"nodeOffset":"4.22 124.28","parent":[0,1,4,5,6,7,8,11,12,13,14,17,18,19,20]},
{"index":22,"nodeOffset":"-10.64 116.28","parent":[0,1,3,5,6,7,8,10,12,13,14,16,18,19,20]},
{"index":23,"nodeOffset":"-23.95 106.42","parent":[0,1,3,4,6,7,8,10,11,13,14,16,17,19,20]},
{"index":24,"nodeOffset":"-35.4 95","parent":[0,1,3,4,5,7,8,10,11,12,14,16,17,18,20]},
{"index":25,"nodeOffset":"-44.75 82.36","parent":[0,1,3,4,5,6,8,10,11,12,13,16,17,18,19]},
{"index":26,"nodeOffset":"-51.8 68.89","parent":[0,1,2,5,6,7,8,9,12,13,14,15,18,19,20,23,24,25]},
{"index":27,"nodeOffset":"-56.47 55","parent":[0,1,2,4,6,7,8,9,11,13,14,15,17,19,20,22,24,25]},
{"index":28,"nodeOffset":"-58.69 41.11","parent":[0,1,2,4,5,7,8,9,11,12,14,15,17,18,20,22,23,25]},
{"index":29,"nodeOffset":"-58.54 27.64","parent":[0,1,2,4,5,6,8,9,11,12,13,15,17,18,19,22,23,24]},
{"index":30,"nodeOffset":"-56.09 15","parent":[0,1,2,3,6,7,8,9,10,13,14,15,16,19,20,21,24,25,28,29]},
{"index":31,"nodeOffset":"-51.54 3.58","parent":[0,1,2,3,5,7,8,9,10,12,14,15,16,18,20,21,23,25,27,29]},
{"index":32,"nodeOffset":"-45.13 -6.28","parent":[0,1,2,3,5,6,8,9,10,12,13,15,16,18,19,21,23,24,27,28]},
{"index":33,"nodeOffset":"-37.16 -14.28","parent":[0,1,2,3,4,7,8,9,10,11,14,15,16,17,20,21,22,25,26,29,32]},
{"index":34,"nodeOffset":"-27.96 -20.18","parent":[0,1,2,3,4,6,8,9,10,11,13,15,16,17,19,21,22,24,26,28,31]},
{"index":35,"nodeOffset":"-17.94 -23.78","parent":[0,1,2,3,4,5,8,9,10,11,12,15,16,17,18,21,22,23,26,27,30]}
],
"config":{
"nodeValueAuto":"none",
"nodeRadius":2,
"algorithm":"Find coverage path",
"indexes":"9,16,2,27,30,7,4,22"
}}Encontrar caminos independientes en un grafo findIndependentPaths()
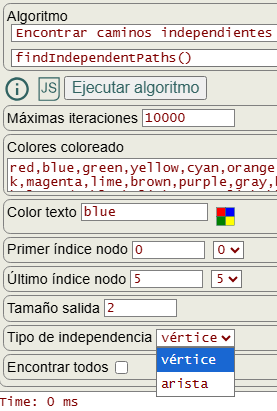
Encontrar caminos con vértices o aristas independientes (vertex or edge independent paths) o también denominados caminos con vértices o aristas disjuntos (vertex or edge disjoint paths) entre dos nodos "s" y "t" de un grafo supone encontrar subconjuntos de caminos donde cada de uno ellos no comparte vértices o aristas con los otros caminos sin incluir "s" y "t".
Los caminos pueden encontrarse con vértices o aristas, pudiendo seleccionarlo en la opción tipo de independencia como vemos en la Figura. En los dos siguientes apartados veremos como encontrar caminos con vértices y con aristas independientes.
Si no se excluyen los nodos inicial y final "s" y "t" estaríamos hablando de caminos con todos los vértices independientes. En este apartado al decir caminos independientes
o caminos con vértices o aristas independientes
nos estaremos refiriendo a caminos con vértices o aristas internamente independientes
en la forma en que los hemos definido excluyendo los extremos del camino, aunque prescindamos del término "internamente".
El código JavaScript para implementar findIndependentPaths() se expone a continuación, recibiendo los argumentos matrix, typeIndependence, firstIndex, lastIndex, outputSize y findAll. Los argumentos path, res y result forman parte de las llamadas internas del recursivo y no es necesario pasarlos inicialmente.
function findIndependentPaths({matrix=[], typeIndependence="vertex", firstIndex=0,
lastIndex=0, outputSize=1, findAll=false, path=[], res=[], result=[]}) {
if (iter++, iter>maxIter) throw new Error(`Maximum iterations ${maxIter} reached`);
try {
let n = matrix.length;
path.push(firstIndex);
if (firstIndex===lastIndex) {
res.push([path]);
if (outputSize===1) {
result.push([path]);
} else {
let duplicatePaths = [];
for (let paths of res) {
let independents = true;
for (let itemPath of paths) {
let temp = areIndependent(itemPath, path, typeIndependence);
if (typeof temp==="string") throw new Error(temp);
independents = temp;
if (!independents) break;
}
if (independents) {
duplicatePaths.push([...paths]);
paths.push(path);
if (paths.length===outputSize) {
result.push([...paths]);
if (!findAll) return result;
}
}
}
for (let paths of duplicatePaths) {
res.push(paths);
}
}
} else {
let parents = getParents({matrix, index:firstIndex});
for (let parent of parents){
if (parent!==firstIndex) {
if (!path.includes(parent)) {
let temp = findIndependentPaths({matrix, typeIndependence,
firstIndex:parent, lastIndex, outputSize, findAll,
path:[...path], res, result});
if (typeof temp==="string") throw new Error(temp);
if (!findAll && temp.length>0) break;
}
}
}
}
} catch(e){result.warnings = [e.message]}
return result;
}El algoritmo es un recursivo del tipo DFS que vimos en el tema anterior, explorando los nodos del grafo en profundidad primero, parando cuando encuentra un camino para comprobar si ese camino tiene vértices (o aristas en otro caso) independientes con los que ya tenemos almacenados. Para ello usamos la siguiente función auxiliar:
function areIndependent(path1=[], path2=[], typeIndependence="vertex") {
let result = true;
try {
let [a, b] = path1.length<path2.length ? [path1, path2] : [path2, path1];
if (typeIndependence==="vertex") {
if (a.length===2 && b.length===2) {
return false;
} else {
for (let i=1; i<a.length-1; i++) {
if (b.includes(a[i])){
return false;
}
}
}
} else {
for (let i=1; i<a.length; i++) {
for (let j=1; j<b.length; j++) {
if (a[i-1]===b[j-1] && a[i]===b[j] || a[i-1]===b[j] && a[i]===b[j-1]){
return false;
}
}
}
}
} catch(e){result = e.message}
return result;
}Encontrar caminos con vértices independientes
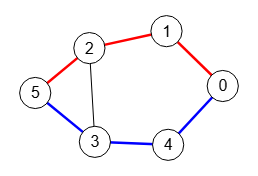
Encontrar caminos con vértices independientes (vertex independent paths) o también denominados caminos con vértices disjuntos (vertex disjoint paths) entre dos nodos "s" y "t" de un grafo supone encontrar subconjuntos de caminos donde cada de uno ellos no comparte vértices con los otros caminos sin incluir "s" y "t".
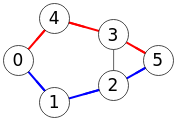
En el grafo de la Figura los dos caminos independientes entre nodos "0" y "5" [0,1,2,5] y [0,4,3,5] no comparten ningún nodo sin incluir "0" y "5".
Time: 1 ms Encontrar caminos con vértices independientes: [[[0,1,2,5],[0,4,3,5]]]
{"nodes":[
{"index":0,"nodeOffset":"74.91 22","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"38.1","parent":[{"index":-1},{"index":0}]},
{"index":2,"nodeOffset":"-7.06 6.8","parent":[{"index":-1},{"index":1}]},
{"index":3,"nodeOffset":"-19.14 44.4","parent":[{"index":-1},{"index":2}]},
{"index":4,"nodeOffset":"-4.1 45.6","parent":[{"index":-1},{"index":3},{"index":0}]},
{"index":5,"nodeOffset":"-71.6 24.8","parent":[{"index":-1},{"index":2},{"index":3}]}
],
"config":{
"algorithm":"Find independent paths",
"lastIndex":5,
"outputSize":2
}}
En la Figura vemos como exportamos a Wolfram usando la función FindVertexIndependentPaths[g, s, t, k], con "s" y "t" el primer y último nodo y con "k" el máximo de caminos a encontrar, pudiendo ser "Infinity" para que Wolfram busque los de mayor tamaño.
g = AdjacencyGraph[{{0,1,0,0,1,0},{1,0,1,0,0,0},{0,1,0,1,0,1},{0,0,1,0,1,1},{1,0,0,1,0,0},{0,0,1,1,0,0}},
ImageSize->177, VertexSize->{"Scaled", 0.18}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center]}, VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindVertexIndependentPaths[g, 1, 6, 2];
e = Table[EdgeList[PathGraph[i]], {i, f}];
c = {Red, Blue, RGBColor["green"], Yellow, Cyan, Orange, Pink, Magenta, Green, Brown, Purple, Gray, Black, RGBColor["lavenderblush"], LightGreen, LightBlue, LightYellow, LightCyan, LightGray};
s = Table[Apply[Style, {i, Part[c, First[First[Position[e, i]]]], Thick}], {i,e}];
HighlightGraph[g, s]
En la Figura se observa las opciones para ejecutar este algoritmo findVertexIndependentPaths(). Podemos configurar una lista de colores para coloreado y el color texto para el caso de aristas con etiquetas. Aparte de establecer el primer y último nodo, vemos las opciones tipo de independencia con vértice seleccionado, tamaño salida que establece el tamaño del número de caminos independientes a explorar y encontrar todos para devolver todos los que se encuentren.
El número de caminos con vértices independientes se podría obtener analizando todos los caminos del grafo. Ejecutando para ese ejemplo findPath() entre los nodos "0" y "5" con la opción de encontrar todos los caminos obtendremos los 4 caminos siguientes: [[0,1,2,3,5], [0,1,2,5], [0,4,3,2,5], [0,4,3,5]]. El algoritmo analiza todas las combinaciones de caminos entre 1 y el máximo número de caminos posibles del grafo, entre 1 y 4 para este ejemplo. Para ello usamos el recursivo combine(list, k), produciendo las siguientes combinaciones de 4 elementos tomados en subconjuntos de 1 hasta 4 elementos:
paths = [[0,1,2,3,5], [0,1,2,5], [0,4,3,2,5], [0,4,3,5]]
list = [0, 1, 2, 3];
combine([0,1,2,3], 1) = {[0,1,2,3,5], [0,1,2,5], [0,4,3,2,5], [0,4,3,5]}
[0,1,2,3,5] ⇒ [[0,1,2,3,5]] ⇒ Independiente
[0,1,2,5] ⇒ [[0,1,2,5]] ⇒ Independiente
[0,4,3,2,5] ⇒ [[0,4,3,2,5]] ⇒ Independiente
[0,4,3,5] ⇒ [[0,4,3,5]] ⇒ Independiente
combine([0,1,2,3], 2) = {[0, 1], [0, 2], [0, 3], [1, 2], [1, 3], [2, 3]}
[0, 1] ⇒ [[0,1,2,3,5], [0,1,2,5]] ⇒ Repite 1,2
[0, 2] ⇒ [[0,1,2,3,5], [0,4,3,2,5]] ⇒ Repite 2,3
[0, 3] ⇒ [[0,1,2,3,5], [0,4,3,5]] ⇒ Repite 3
[1, 2] ⇒ [[0,1,2,5], [0,4,3,2,5]] ⇒ Repite 2
[1, 3] ⇒ [[0,1,2,5], [0,4,3,5]] ⇒ Independientes
[2, 3] ⇒ [[0,4,3,2,5], [0,4,3,5]] ⇒ Repite 4,3
combine([0,1,2,3], 3) = {[0, 1, 2], [0, 1, 3], [0, 2, 3], [1, 2, 3]}
[0, 1, 2] ⇒ [[0,1,2,3,5], [0,1,2,5], [0,4,3,2,5]] ⇒ Repite 1,2,3
[0, 1, 3] ⇒ [[0,1,2,3,5], [0,1,2,5], [0,4,3,5]] ⇒ Repite 1,2,3
[0, 2, 3] ⇒ [[0,1,2,3,5], [0,4,3,2,5], [0,4,3,5]] ⇒ Repite 2,3,4
[1, 2, 3] ⇒ [[0,1,2,5], [0,4,3,2,5], [0,4,3,5]] ⇒ Repite 2,3,4
combine([0,1,2,3], 4) = {[0, 1, 2, 3]}
[0, 1, 2, 3] ⇒ [[0,1,2,3,5], [0,1,2,5], [0,4,3,2,5], [0,4,3,5]] ⇒ Repite 1,2,3,4 Para combinaciones de 1 elemento se obtienen resultados con un único camino que se consideran independientes. Para el resto se seleccionan aquellos cuyos nodos a excepción del "0" y "5" no se repiten, observando que sólo hay un caso [[0,1,2,5], [0,4,3,5]]
Ese planteamiento es válido cuando el número de caminos entre dos nodos en un grafo no es muy alto. Pero como ya hemos visto en apartados anteriores, para grafos más complejos no se obtienen todos los resultados con findPath(). El algoritmo findIndependentPaths() que finalmente se implementa no usa ese planteamiento sino otro basado en búsqueda en profundidad como veremos al final de este apartado.
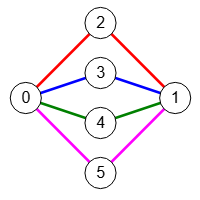
En la Figura vemos un grafo donde sus 4 caminos son idependientes entre los nodos "0" y "1", resaltándose cada uno con un color diferente. Si iteramos con tamaño de salida entre 1 y 4 encontraremos 4 con 1 camino, 6 con 2 caminos, 4 con 3 caminos y 1 con 4 caminos, como se observa en el siguiente esquema.
Si seguimos iterando a partir de 5 caminos veremos que no encuentra ningún resultado, por lo que 4 caminos independientes es el número máximo, algo que para este simple grafo es obvio observando la Figura. Más abajo volveremos sobre esto.
Encontrar caminos con vértices independientes: 1 CAMINO [[[0,2,1]], [[0,3,1]], [[0,4,1]], [[0,5,1]]] 2 CAMINOS [[[0,2,1],[0,3,1]], [[0,2,1],[0,4,1]], [[0,2,1],[0,5,1]], [[0,3,1],[0,4,1]], [[0,3,1],[0,5,1]], [[0,4,1],[0,5,1]]] 3 CAMINOS [[[0,2,1],[0,3,1],[0,4,1]], [[0,2,1],[0,3,1],[0,5,1]], [[0,2,1],[0,4,1],[0,5,1]], [[0,3,1],[0,4,1],[0,5,1]]] 4 CAMINOS [[[0,2,1],[0,3,1],[0,4,1],[0,5,1]]]
Con este JSON se importa el ejemplo con el tamaño de 4 caminos:
{"nodes":[
{"index":0,"nodeOffset":"5.71 27.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"51.43 27.5","parent":[{"index":-1}]},
{"index":2,"nodeOffset":"7.14 -2.5","parent":[{"index":-1},{"index":0},{"index":1}]},
{"index":3,"nodeOffset":"-7.14 17.5","parent":[{"index":-1},{"index":0},{"index":1}]},
{"index":4,"nodeOffset":"-21.43 37.5","parent":[{"index":-1},{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"-35.71 57.5","parent":[{"index":-1},{"index":0},{"index":1}]}
],
"config":{
"algorithm":"Find independent paths",
"colorsForColoring":"red,blue,green,magenta",
"lastIndex":1,
"outputSize":4
}}
En la Figura vemos como se exporta a Wolfram ese ejemplo. Como en el código f = FindVertexIndependentPaths[g, 1, 2, 4] que busca como máximo 4 caminos. Si usarámos en su lugar "Infinity" Wolfram busca hasta el máximo número posible de caminos independientes, devolviendo también ese máximo con 4 caminos independientes pues no hay superiores, tal como también resulta en nuestra aplicación. Aparte de la ubicación de los nodos es exactamente el mismo resultado obtenido en la aplicación.
g = AdjacencyGraph[{{0,0,1,1,1,1},{0,0,1,1,1,1},{1,1,0,0,0,0},{1,1,0,0,0,0},{1,1,0,0,0,0},{1,1,0,0,0,0}},
ImageSize->200, VertexSize->{"Scaled", 0.16}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center]}, VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindVertexIndependentPaths[g, 1, 2, 4];
e = Table[EdgeList[PathGraph[i]], {i, f}];
c = {Red, Blue, RGBColor["green"], Magenta};
s = Table[Apply[Style,{i, Part[c, First[First[Position[e, i]]]], Thick}], {i,e}];
HighlightGraph[g, s]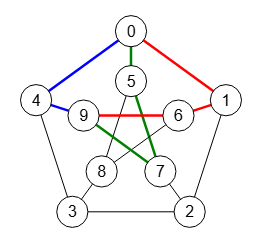
En el grafo de Petersen de la Figura hay 4 combinaciones de caminos de tamaño 3 con vértices independientes entre los nodos "0" y "9", accediendo al segundo de ellos usando el botón para el mostrado, resaltándose el segundo en el resultado que devuelve la aplicación:
Time: 1 ms Encontrar caminos independientes vértice: [[[0,1,2,3,8,6,9],[0,4,9],[0,5,7,9]], [[0,1,6,9],[0,4,9],[0,5,7,9]], [[0,1,6,9],[0,4,9],[0,5,8,3,2,7,9]], [[0,1,2,7,9],[0,4,9],[0,5,8,6,9]]]
{"nodes":[
{"index":0,"nodeOffset":"2.5","parent":-1},
{"index":1,"nodeOffset":"65.54 2.64","parent":0},
{"index":2,"nodeOffset":"51.01 22.36","parent":1},
{"index":3,"nodeOffset":"-4.34 -2.64","parent":2},
{"index":4,"nodeOffset":"-35.54 2.64","parent":[0,3]},
{"index":5,"nodeOffset":"-22.5 -5","parent":0},
{"index":6,"nodeOffset":"21.52 -16.18","parent":1},
{"index":7,"nodeOffset":"-2.41 -18.82","parent":[2,5]},
{"index":8,"nodeOffset":"-9.26 -43.82","parent":[3,5,6]},
{"index":9,"nodeOffset":"-41.52 -16.18","parent":[4,6,7]}
],
"config":{
"algorithm":"Find independent paths",
"lastIndex":9,
"outputSize":3,
"findAll":true
}}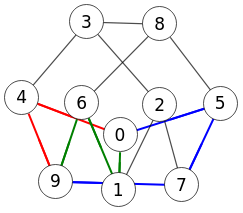
En la Figura vemos como se exporta a Wolfram ese ejemplo. La ubicación de los nodos no es igual, observando que el nodo "1" esta ubicado encima de la arista "9-7", pero es exactamente el mismo grafo con el resultado [[0,1,6,9], [0,4,9], [0,5,7,9]], uno de los que encontramos también en nuestra aplicación.
g = AdjacencyGraph[{{0,1,0,0,1,1,0,0,0,0},{1,0,1,0,0,0,1,0,0,0},{0,1,0,1,0,0,0,1,0,0},{0,0,1,0,1,0,0,0,1,0},{1,0,0,1,0,0,0,0,0,1},
{1,0,0,0,0,0,0,1,1,0},{0,1,0,0,0,0,0,0,1,1},{0,0,1,0,0,1,0,0,0,1},{0,0,0,1,0,1,1,0,0,0},{0,0,0,0,1,0,1,1,0,0}},
ImageSize->243, VertexSize->{"Scaled", 0.13}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center], 7->Placed[6,Center], 8->Placed[7,Center], 9->Placed[8,Center],
10->Placed[9,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindVertexIndependentPaths[g, 1, 10, 3]
e = Table[EdgeList[PathGraph[i]], {i, f}];
c = {Red, Blue, RGBColor["green"], Yellow, Cyan, Orange, Pink, Magenta, Green, Brown, Purple, Gray, Black, RGBColor["lavenderblush"], LightGreen, LightBlue, LightYellow, LightCyan, LightGray};
s = Table[Apply[Style, {i, Part[c, First[First[Position[e, i]]]], Thick}], {i,e}];
HighlightGraph[g, s]Si en lugar de FindVertexIndependentPaths[g, 1, 10, 3] ponemos FindVertexIndependentPaths[g, 1, 10, Infinity] veremos que encuentra el mismo resultado sin que se aprecie un incremento en el tiempo de ejecución. Es posible que Wolfram use VertexConnectivity para obtener el grado de conectividad o FindMaximumFlow para obtener el valor del máximo flujo, resultando que esos números son iguales que el mayor resultado con 3 caminos, como vemos si agregamos este código:
(* Maximum number of independent paths *)
f
Length[f]
VertexConnectivity[g, 1,10]
FindMaximumFlow[g, 1, 10]
Resultando que Length[f] = 3, VertexConnectivity[g, 1, 10] = 3, y FindMaximumFlow[g, 1, 10] = 3 con lo que no se necesitaría explorar todos los tamaños cuando se pase "Infinity" sino sólo ese grado 3 de conectividad o máximo flujo.
En la aplicación implementamos encontrar máximo flujo con findMaximumFlow() y encontrar caminos con aristas independientes usando máximo flujo findEdgeIndependentPathsMaxFlow() que nos permitirá encontrar caminos independientes de forma más eficiente, aunque con aristas en lugar de vértices. En el siguiente tema trataremos ese asunto.
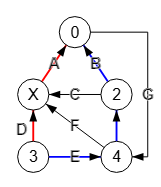
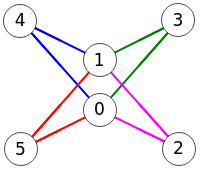
En la Figura vemos que también podemos buscar caminos con vértices independientes en un grafo dirigido. En este caso con la opción de encontrar todos entre los nodos "3" y "0" vemos que encuentra 1 resultado con tamaño de 2 caminos, presentándose en la imagen anterior el primero de ellos.
Cuando uno o más nodos tienen valores diferentes a sus índices, la aplicación presenta también el resultado con esos valores, lo que sucede con el nodo con índice "1" que tiene el valor "X":
Time: 0 ms Encontrar caminos independientes vértice: [[[3,1,0],[3,4,2,0]]] Valores de nodos de camino ⇒ [[3,"X",0],[3,4,2,0]]
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"value":"X","parent":[{"index":0,"value":"A"}]},
{"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"C"}]},
{"index":3,"parent":[{"index":1,"value":"D","lineTextOffset":"-0.75 0.25"},{"index":4,"value":"E"}]},
{"index":4,"parent":[{"index":1,"value":"F"},{"index":2},{"index":0,"lineOffset":"1","markerReverse":true,"value":"G"}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find independent paths",
"firstIndex":3,
"outputSize":2,
"findAll":true
}}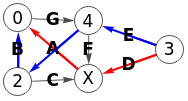
En la Figura vemos como se exporta a Wolfram el ejemplo anterior.
g = AdjacencyGraph[{{0,0,0,0,1},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}}, ImageSize->188,
VertexSize->{"Scaled", 0.17}, VertexLabels->{1->Placed[0,Center], 2->Placed["X",Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(2->1)->"A", (3->1)->"B", (3->2)->"C", (4->2)->"D", (4->5)->"E", (5->2)->"F", (1->5)->"G"},
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindVertexIndependentPaths[g, 4, 1, 2];
e = Table[EdgeList[PathGraph[i, DirectedEdges->True]], {i, f}];
c = {Red, Blue, RGBColor["green"], Yellow, Cyan, Orange, Pink, Magenta, Green, Brown, Purple, Gray,
Black, RGBColor["lavenderblush"], LightGreen, LightBlue, LightYellow, LightCyan, LightGray};
s = Table[Apply[Style,{i, Part[c, First[First[Position[e, i]]]], Thick}], {i,e}];
HighlightGraph[g, s]Encontrar caminos con aristas independientes
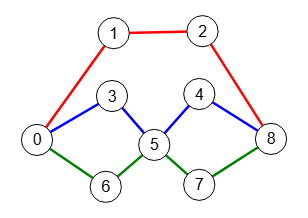
Encontrar caminos con aristas independientes (edge independent paths) o también denominados caminos con aristas disjuntas (edge disjoint paths) entre dos nodos "s" y "t" de un grafo supone encontrar subconjuntos de caminos donde cada de uno ellos no comparte aristas con los otros caminos, aunque pudieran compartir nodos.
En la Figura vemos un grafo con 3 aristas independientes. Observe que el nodo "5" se comparte entre los caminos rojo y verde. Si tratamos de encontrar caminos con vértices independientes que vimos en el apartado anterior, este caso no sería incluido pues ese nodo "5" está compartido. Sin embargo al tratarse de aristas lo que se tiene en cuenta es que no se compartan dichas aristas.
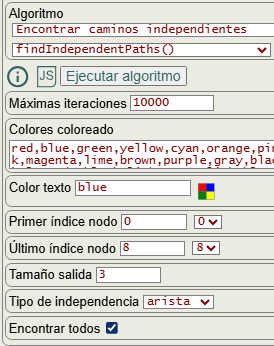
En la Figura vemos las opciones para encontrar caminos con aristas independientes, que son las mismas que vimos en el apartado anterior: colores coloreado con una lista de colores para los diferentes caminos, color texto para el caso de etiquetas de aristas, primer y último índice de nodo, tamaño de salida para el número de caminos a buscar, tipo independencia que es "arista" en este caso y encontrar todos para devolver todos los resultados posibles.
La aplicación devuelve dos resultados con 3 caminos, presentándose en la Figura el primero de ellos:
Time: 0 ms Encontrar caminos con aristas independientes: [[[0,1,2,8],[0,3,5,4,8],[0,6,5,7,8]], [[0,1,2,8],[0,3,5,7,8],[0,6,5,4,8]]]
Con este JSON puede importar el ejemplo:
{"nodes":[
{"index":0,"nodeOffset":"4.8 43.6","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"25.47 0.8","parent":[{"index":-1},{"index":0}]},
{"index":2,"nodeOffset":"51","parent":[{"index":-1},{"index":1}]},
{"index":3,"nodeOffset":"4.8 26","parent":[{"index":-1},{"index":0}]},
{"index":4,"nodeOffset":"29.73 25.2","parent":[{"index":-1}]},
{"index":5,"nodeOffset":"1.71 45.6","parent":[{"index":-1},{"index":3},{"index":4}]},
{"index":6,"nodeOffset":"-27.7 62.4","parent":[{"index":-1},{"index":0},{"index":5}]},
{"index":7,"nodeOffset":"-0.31 61.6","parent":[{"index":-1},{"index":5}]},
{"index":8,"nodeOffset":"18.4 43.2","parent":[{"index":-1},{"index":4},{"index":7},{"index":2}]}
],
"config":{
"algorithm":"Find independent paths",
"lastIndex":8,
"outputSize":3,
"typeIndependence":"edge",
"findAll":true
}}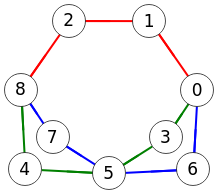
En la Figura vemos el resultado al exportar a Wolfram con la función FindEdgeIndependentPaths[g, s, t, k], con "s" y "t" el primer y último nodo y con "k" el máximo de caminos a encontrar, pudiendo ser "Infinity" para que Wolfram busque los de mayor tamaño.
Encuentra el mismo resultado que en la aplicación [[0,1,2,8], [0,3,5,4,8], [0,6,5,7,8]].
g = AdjacencyGraph[{{0,1,0,1,0,0,1,0,0},{1,0,1,0,0,0,0,0,0},{0,1,0,0,0,0,0,0,1},{1,0,0,0,0,1,0,0,0},{0,0,0,0,0,1,0,0,1},
{0,0,0,1,1,0,1,1,0},{1,0,0,0,0,1,0,0,0},{0,0,0,0,0,1,0,0,1},{0,0,1,0,1,0,0,1,0}}, ImageSize->219,
VertexSize->{"Scaled", 0.14}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center], 7->Placed[6,Center], 8->Placed[7,Center],
9->Placed[8,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindEdgeIndependentPaths[g, 1, 9, 3];
e = Table[EdgeList[PathGraph[i]], {i, f}];
c = {Red, Blue, RGBColor["green"], Yellow, Cyan, Orange, Pink, Magenta, Green, Brown, Purple, Gray,
Black, RGBColor["lavenderblush"], LightGreen, LightBlue, LightYellow, LightCyan, LightGray};
s = Table[Apply[Style,{i, Part[c, First[First[Position[e, i]]]], Thick}], {i,e}];
HighlightGraph[g, s]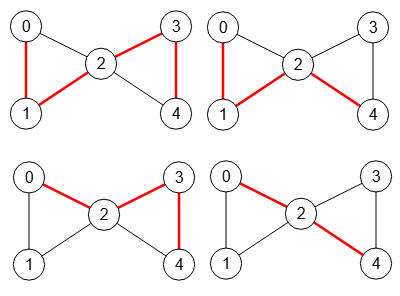
Para comprobar las diferencias entre encontrar caminos con vértices y aristas independientes, vemos en la Figura en primer lugar los 4 resultados con 1 camino con vértices independientes, no habiendo con tamaños 2 o superiores.
Time: 0 ms Encontrar caminos independientes vértice: [[[0,1,2,3,4]], [[0,1,2,4]], [[0,2,3,4]], [[0,2,4]]]
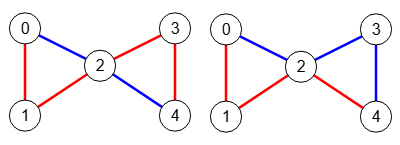
En cambio con aristas independientes, además de los anteriores, también encuentra 2 resultados con 2 caminos que vemos en la Figura, notando que los caminos comparten el nodo "2".
Time: 0 ms Encontrar caminos independientes arista: [[[0,1,2,4],[0,2,3,4]], [[0,1,2,3,4],[0,2,4]]]]
Con este JSON podrá importar el ejemplo:
{"nodes":[
{"index":0,"nodeOffset":"3.33 2.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"-13.33 37.5","parent":[{"index":-1},{"index":0}]},
{"index":2,"nodeOffset":"0 17.5","parent":[{"index":-1},{"index":0},{"index":1}]},
{"index":3,"nodeOffset":"13.33 2.5","parent":[{"index":-1},{"index":2}]},
{"index":4,"nodeOffset":"-3.33 37.5","parent":[{"index":-1},{"index":2},{"index":3}]}
],
"config":{
"algorithm":"Find independent paths",
"lastIndex":4,
"outputSize":2,
"typeIndependence":"edge",
"findAll":true
}}
En la Figura vemos la exportación a Wolfram, donde expone el mismo que el primero que encontramos, aunque con los colores invertidos.
g = AdjacencyGraph[{{0,1,1,0,0},{1,0,1,0,0},{1,1,0,1,1},{0,0,1,0,1},{0,0,1,1,0}},
ImageSize->163, VertexSize->{"Scaled", 0.19}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindEdgeIndependentPaths[g, 1, 5, Infinity];
e = Table[EdgeList[PathGraph[i]], {i, f}];
c = {Red, Blue, RGBColor["green"], Yellow, Cyan, Orange, Pink, Magenta, Green, Brown, Purple, Gray,
Black, RGBColor["lavenderblush"], LightGreen, LightBlue, LightYellow, LightCyan, LightGray};
s = Table[Apply[Style,{i, Part[c, First[First[Position[e, i]]]], Thick}], {i,e}];
HighlightGraph[g, s]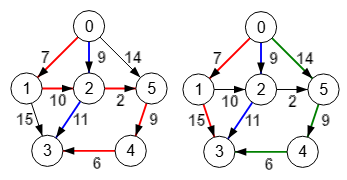
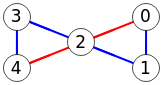
En la Figura vemos a la izquierda uno de los resultados con 2 caminos con aristas independientes entre los nodos "0" y "3" para un grafo dirigido, observando que los caminos comparten el nodo "2". Este es el resultado para un tamaño de salida:
Time: 0 ms Encontrar caminos independientes arista: [[[0,1,2,5,4,3],[0,2,3]], [[0,1,3],[0,2,3]], [[0,1,2,3],[0,2,5,4,3]], [[0,1,3],[0,2,5,4,3]], [[0,2,3],[0,5,4,3]], [[0,1,2,3],[0,5,4,3]],[[0,1,3],[0,5,4,3]]]
Mientras que para un tamaño 3 se obtiene un único resultado que es el que vemos en la parte derecha de la Figura, con este resultado:
Time: 0 ms Encontrar caminos independientes arista: [[[0,1,3],[0,2,3],[0,5,4,3]]]
Con este JSON puede importar el ejemplo:
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0,"value":7,"lineTextOffset":-0.8}]},
{"index":2,"parent":[{"index":0,"value":9,"lineTextOffset":0.8},{"index":1,"value":10,"lineTextOffset":"0 0.8"}]},
{"index":3,"parent":[{"index":1,"value":15,"lineTextOffset":-0.8},{"index":4,"value":6,"lineTextOffset":"0.5 0.8"},{"index":2,"value":11,"lineTextOffset":0.8}]},
{"index":4,"parent":[{"index":5,"value":9,"lineTextOffset":0.8}]},
{"index":5,"parent":[{"index":0,"value":14,"lineTextOffset":0.8},{"index":2,"value":2,"lineTextOffset":"0 0.8"}]}
],
"config":{
"markerStart":"arrow",
"algorithm":"Find independent paths",
"lastIndex":3,
"outputSize":3,
"typeIndependence":"edge",
"findAll":true
}}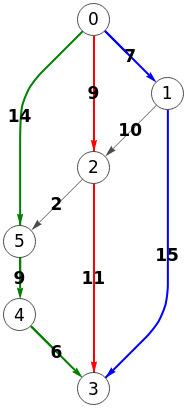
Este ejemplo con tamaño 3 se exporta a Wolfram como vemos en la Figura, observando que son los mismos 3 caminos con aristas independientes que encontramos.
Hacemos un ajuste en los círculos de los vértices a 0.5 pues con el tamaño automático eran muy grandes.

g = AdjacencyGraph[{{0,1,1,0,0,1},{0,0,1,1,0,0},{0,0,0,1,0,1},{0,0,0,0,0,0},{0,0,0,1,0,0},{0,0,0,0,1,0}},
ImageSize->188, VertexSize->{"Scaled", 0.08}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center]},
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(1->2)->7, (1->3)->9, (2->3)->10, (2->4)->15, (5->4)->6, (3->4)->11, (6->5)->9, (1->6)->14, (3->6)->2},
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
f = FindEdgeIndependentPaths[g, 1, 4, 3];
e = Table[EdgeList[PathGraph[i, DirectedEdges->True]], {i, f}];
c = {Red, Blue, RGBColor["green"], Yellow, Cyan, Orange, Pink, Magenta, Green, Brown, Purple, Gray, Black,
RGBColor["lavenderblush"], LightGreen, LightBlue, LightYellow, LightCyan, LightGray};
s = Table[Apply[Style,{i, Part[c, First[First[Position[e, i]]]], Thick}], {i,e}];
HighlightGraph[g, s]