Acciones sobre grafos
Acciones sobre un grafo

En la sección de acciones de Grafos SVG ejecutamos algoritmos sobre un grafo. Estas acciones pueden ser muy simples como obtener el número de vértices de un grafo. O más complejos como colorear un grafo que es lo que muestra la Figura.
Todos los algoritmos se ejecutan sobre la matriz de adyacencia devolviendo un resultado, pero sin modificarla. Algunos requerirán además otros argumentos que aparecerán en el panel de la Figura. Algunos algoritmos modifican la presentación, como en el coloreado de nodos o para resaltar caminos o ciclos. Además al JSON que se exporte se le agrega el nombre del algoritmo y los argumentos o parámetros de ejecución.
El resultado de los algoritmos será una variable de JavaScript tipos Number, Boolean, Array, Object u otros, pero nunca un String. La aplicación trata cada resultado convirtiéndolo en texto y volcándolo en el área de texto inferior que se observa en la Figura, agregando el tiempo de ejecución y comentarios en algunos casos.
El resultado de tipo String se reserva para el control de errores en los algoritmos, pues cuando se produce un error que interceptamos con try {...} catch(e){result = e.message} return result devolvemos el mensaje de error como un String, para así desde el punto de llamada de la función detectarlo con algo como if (typeof x==="string") throw new Error(x). Si necesitáramos devolver un tipo String lo encerramos en un Object o en un Array.
El control máximas iteraciones con un valor inicial de 10.000 iteraciones sirve para cortar la ejecución de algunos algoritmos cuando se llegue a ese límite, especialmente los recursivos, con lo que evitamos que se colapse el navegador.
El botón nos lleva a información del algoritmo en páginas de esta serie de temas. Si no hay información publicada vinculará con la página de inicio. El botón nos presenta un panel con el código JavaScript del algoritmo, código que actualmente está usando la aplicación, pues pudiera ser que hubiese hecho modificaciones sin actualizar el que aparece en estas páginas.
En el ÍNDICE al inicio de esta página se relacionan todos los algoritmos que hay actualmente en la aplicación. Aquellas entradas que tengan un vínculo significa que he publicado esa acción en algún tema de este sitio. Algunos ya los he incluido en temas anteriores. Otros los expondré en este tema y siguientes. La siguiente lista expone los primeros grupos, resaltando aquellos que se exponen en este tema. Seguramente iré incorporando más algoritmos por lo que esta lista no es exhaustiva, pudiendo consultar el ÍNDICE mencionado que siempre contendrá una lista actualizada de todos los recursos.
- Acciones básicas que son acciones para contar vértices o aristas, grados de los vértices y otras cosas básicas sobre grafos, encontrando obtener total vértices getTotalVertexs(), obtener total de aristas getTotalEdges(), obtener grados de los vértices getVertexDegrees() y obtener grados entrada/salida de los vértices getVertexInOutDegrees() en este tema. Y modo valores de la matriz getMatrixModeValue() que vimos en un tema anterior. En el tema siguiente veremos otras acciones básicas 2 que tienen que ver con la conversión entre matriz de adyacencia y lista de aristas, lista de adyacencias, matriz de indicencias y matriz de distancias.
- Direccionalidad sobre las direcciones de un grafo, con acciones como es el grafo dirigido isGraphDirected(), obtener dirección getDirection(), obtener matriz no dirigida getUndirectedMatrix(), obtener matriz dirigida getDirectedMatrix(), todos en un tema anterior.
- Vecindad que obtiene padres, hijos y vecinos, como obtener padres getParents(), obtener hijos getChildren() y obtener vecinos getNeighbors(), todos en un tema anterior.
- Ciclos en un grafo, con tiene ciclos hasCycles(), obtener ciclos desde nodo getCyclesFromNode() y obtener todos los ciclos getCyclesAll() todos en este tema.
- Tipología que nos dice si un grafo cumple alguna característica. En temas anteriores ya expuse es el grafo multigrafo isMultiGraph(), es el grafo completo isGraphComplete(), es el grafo bipartito isGraphBipartite() y es el grafo bipartito completo isGraphBipartiteComplete(). Aún no he publicado la acción es el grafo un árbol isGraphTree(), pues es necesario ver primero los algoritmos de conectividad que a su vez necesitan los de búsqueda.
En temas siguientes expondré el resto de algoritmos en estos grupos:
- Ciclo Hamiltoniano
- Búsqueda en grafos
- Conectividad en grafos
- Coloreado de un grafo
- Árbol recubrimiento mínimo (MST)
- Camino mínimo
- Subgrafos
- Cliques
- Isomorfismo de grafos
Obtener total vértices getTotalVertexs()

La acción obtener total vértices devuelve el número de vértices de un grafo. Como se observa en la Figura, todos los algoritmos se ejecutan sobre la matriz de adyacencia del grafo, devolviendo un resultado dependiendo del tipo de acción.
Esta acción de obtener el número de vértices es muy simple, pues sólo se trata de devolver la longitud de la matriz de adyencia matrix.length, como se observa en el código de la función getTotalVertexs({matrix}):
function getTotalVertexs({matrix=[]}) {
return matrix.length;
}
Aplicándolo sobre el grafo de muestra de la Figura, que puede encontrar en la sección de muestras mediante el botón , obtenemos el resultado siguiente, donde se informa del tiempo de ejecución, insignificante en este caso, y del resultado.
Time: 0 ms Obtener total de vértices: 5
Si tras la ejecución del algoritmo se exporta a JSON veremos que incluye "algorithm":"Get total vertexs" en la configuración. Importando este JSON se dibujará el grafo y luego se ejecutará ese algoritmo.
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"value":"X","parent":[{"index":0,"value":"A"}]},
{"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"C"}]},
{"index":3,"parent":[{"index":1,"value":"D","lineTextOffset":"-0.75 0.25"},{"index":4,"value":"E"}]},
{"index":4,"parent":[{"index":1,"value":"F"},{"index":2},{"index":0,"lineOffset":"1","markerReverse":true,"value":"G"}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Get total vertexs"
}}
Al exportar a Wolfram Cloud se agrega el código que Wolfram usa para conseguir el resultado. Como vemos en la Figura, la función equivalente es VertexCount[g]. Recordando que en Wolfram Cloud cada línea de código es una sentencia que devuelve un resultado, si hay un punto y coma al final no se mostrará el resultado. Con la opción ocultar resultados previos no agregamos el punto y coma, mostrándose los resultados previos, pues el resultado de la última línea siempre se mostrará.
Los valores de ajustar tamaños son factores que mayores que uno incrementan y menores reducen los tamaños de la imagen, vértices, textos y grueso de aristas. En general la vista en Wolfram suele ser similar, pero en ciertos casos hay que aplicar algún ajuste de esos tamaños.

En la Figura vemos el resultado del código Wolfram que exponemos más abajo. Es el mismo grafo, aunque con otra disposición de los nodos. A continuación del grafo se muestra el resultado "5" de la ejecución de VertexCount[g].
En la página VertexCount de Wolfram Cloud así como en Vertex Count en Wolfram MathWorld encontrará más información.
g = AdjacencyGraph[{{0,0,0,0,1},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}}, ImageSize -> 188,
VertexSize -> {"Scaled", 0.17}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed["X",Center], 3 -> Placed[2,Center],
4 -> Placed[3,Center], 5 -> Placed[4,Center]}, VertexLabelStyle -> Directive[Black,17.5],
EdgeLabelStyle -> Directive[Black,17.5,Bold], EdgeLabels -> {(2->1)->"A", (3->1)->"B", (3->2)->"C", (4->2)->"D", (4->5)->"E", (5->2)->"F", (1->5)->"G"},
VertexStyle -> White, DirectedEdges -> True, EdgeStyle -> {{Black,Thickness[0.005]}}]
VertexCount[g]Obtener total de aristas getTotalEdges()

La acción obtener total de aristas cuenta las aristas de un grafo. En la Figura vemos la ejecución sobre un grafo dirigido con un autobucle. Vemos que el grafo se clasifica como multigrafo (autobucles), exponiendo el aviso El grafo es multigrafo y el algoritmo podría no ejecutarse correctamente
. El motivo de este aviso así como del control forzar dirigido lo explicaremos más abajo. El resultado que se obtiene con ese control desactivado por defecto es el siguiente, contando 6 aristas:
Time: 0 ms Obtener total de aristas: 6
El código JavaScript de getTotalEdges() es el siguiente, usando isGraphDirected() que ya expusimos en un tema anterior:
function getTotalEdges({matrix=[], forceDirected=false}) {
let result = 0;
try {
let directed = forceDirected || isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
let n = matrix.length;
for (let i=0; i<n; i++) {
for (let j=0; j<=i; j++) {
if (matrix[i][j]!==0) result++;
if (i!==j && directed && matrix[j][i]!==0) result++;
}
}
} catch(e){result = e.message}
return result;
}0 0 0 0 1 0 0 0 1 1 1 0 1 0 1 0
Sobre la matriz de adyacencia iteramos contando las relaciones matrix[i][j]!==0 o, si es dirigido, matrix[j][i]!==0. De ahí la necesidad de usar la función sGraphDirected(). O forzar dirigido con el argumento forceDirected cuya utilidad explicaremos más abajo.

En la Figura vemos el grafo de ejemplo, que puede importar desde la sección de muestras a la que se accede con el botón , o bien importando el JSON siguiente.
{"nodes":[
{"index":0,"nodeOffset":"-4","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"16 -5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-4 -10","parent":[{"index":1},{"index":0,"lineOffset":10.37,"lineType":"quadratic"},{"index":2,"lineType":"cubic","lineOffset":"-4 4 4 4"}]},
{"index":3,"nodeOffset":"-24 -55","parent":[{"index":2},{"index":0}]}
],
"config":{
"wv":73,
"hv":77,
"width":182.51,
"height":192.5,
"adjust":false,
"wvIni":73,
"markerEnd":"arrow",
"algorithm":"Get total edges"
}}
La exportación a Wolfram Cloud puede verla en la Figura, exponiendo el resultado de 6 aristas usando la función EdgeCount[g], encontrando más información en Edge Count de Wolfram MathWorld.

No sé cuál es el motivo por el que la arista "2🡒0" aparece con un grueso de línea más débil. Para hacerla visible tenemos que ajustar el grueso de aristas, como se observa en la Figura, con un factor de 1.7
El código Wolfram se expone a continuación.
g = AdjacencyGraph[{{0,0,0,0},{1,0,0,0},{1,1,1,0},{1,0,1,0}}, ImageSize -> 193, VertexSize -> {"Scaled", 0.16},
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center]},
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White,
DirectedEdges -> True, EdgeStyle -> {{Black,Thickness[0.0085]}}]
EdgeCount[g]
Al grafo anterior le agregamos a la arista "3🡒2" otra arista "2🡒3", teniendo entonces una arista doble o todo dirigida "2🡘3", como se observa en la Figura.
0 0 0 0
1 0 0 0
1 1 1 1
1 0 1 0En la matriz de adyacencia vemos el "1" en la posicion (2,3) que es la nueva arista "2🡒3". Ahora el resultado es obviamente de 7 aristas.
Time: 0 ms Obtener total de aristas: 7
Este grafo es también un multigrafo con autobucles y múltiples aristas. Puede importarlo con el siguiente JSON.
{"nodes":[
{"index":0,"nodeOffset":"-4","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"16 -5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-4 -10","parent":[{"index":1},{"index":0,"lineOffset":10.37,"lineType":"quadratic"},{"index":3,"lineType":"quadratic","lineOffset":"-2 2"},{"index":2,"lineType":"cubic","lineOffset":"-4 4 4 4"}]},
{"index":3,"nodeOffset":"-24 -55","parent":[{"index":2},{"index":0}]}
],
"config":{
"wv":73,
"hv":77,
"width":182.51,
"height":192.5,
"adjust":false,
"wvIni":73,
"markerEnd":"arrow",
"algorithm":"Get total edges"
}}
Exportando a Wolfram Cloud obtenemos el resultado de la Figura contando también 7 aristas. Vea que ahora la disposición de los nodos en Wolfram no se parece en nada a la de la Figura, algo que no entiendo muy bien pues la única diferencia es la existencia de la nueva arista "2🡒3".
g = AdjacencyGraph[{{0,0,0,0},{1,0,0,0},{1,1,1,1},{1,0,1,0}}, ImageSize -> 193,
VertexSize -> {"Scaled", 0.16}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center]},
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White, DirectedEdges -> True,
EdgeStyle -> {{Black,Thickness[0.005]}}]
EdgeCount[g]
Veamos ahora el motivo del aviso en color rojo sobre multigrafos y el control forzar dirigido que exponíamos al inicio de este apartado en la Figura.
0 1 1 1 1 0 1 0 1 1 1 1 1 0 1 0
Para ello convertiremos todas las aristas en aristas dobles o todo dirigidas. A excepción del autobucle, pues no es posible representar en la matriz de adyacencia un autobucle doblemente dirigido. Vea que la matriz de adyacencia tiene "1" en todas las posiciones menos la diagonal, donde aparece el autobucle en la posición (2,2).
En estas condiciones si no se especifica otra cosa, esa matriz de adyacencia configura un grafo no dirigido, pues cuando todas las aristas son doblemente dirigidas no hay forma de diferenciar su matriz de adyacencia de un grafo no dirigido.
En el apartado multigrafos y las limitaciones de la matriz de adyacencia de un tema anterior explicamos más sobre esto. Una forma de evitarlo es usar un control externo a la matriz de adyacencia que fuerce a dirigido ese grafo. Y ese es el cometido del control forzar dirigido, como se observa en el siguiente JSON para importar el grafo anterior con la configuración "forceDirected":true.
{"nodes":[
{"index":0,"nodeOffset":"8.17","parent":[{"index":-1},{"index":2},{"index":1,"lineType":"quadratic","lineOffset":"3 -3"},{"index":3,"lineOffset":"-3 -3","lineType":"quadratic"}]},
{"index":1,"nodeOffset":"16 -5","parent":[{"index":0},{"index":2,"lineType":"quadratic","lineOffset":"3 3"}]},
{"index":2,"nodeOffset":"-16.17 40","parent":[{"index":1},{"index":0,"lineOffset":10.37,"lineType":"quadratic"},{"index":3,"lineType":"quadratic","lineOffset":"-2 2"},{"index":2,"lineType":"cubic","lineOffset":"-4 4 4 4"}]},
{"index":3,"nodeOffset":"-24 -55","parent":[{"index":2},{"index":0}]}
],
"config":{
"wv":73,
"hv":77,
"width":182.51,
"height":192.5,
"adjust":false,
"wvIni":73,
"markerEnd":"arrow",
"algorithm":"Get total edges",
"forceDirected":true
}}
En la Figura vemos el resultado de 11 aristas del grafo todo dirigido activando el control forzar dirigido. Si lo desactiva resultará que el algoritmo identifica la matriz de adyacencia como la de un grafo no dirigido y el resultado será de 6 aristas.

Exportando a Wolfram vemos que cuenta también las 11 aristas. Es posible que Wolfram use la propiedad DirectedEdges -> True para diferenciar el grafo de uno no dirigido. Es fácil comprobar que si eliminamos esa propiedad, Wolfram representará un grafo no dirigido contando 6 aristas.
g = AdjacencyGraph[{{0,1,1,1},{1,0,1,0},{1,1,1,1},{1,0,1,0}}, ImageSize -> 193, VertexSize -> {"Scaled", 0.16},
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center]},
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold],
VertexStyle -> White, DirectedEdges -> True, EdgeStyle -> {{Black,Thickness[0.005]}}]
EdgeCount[g]Obtener grados de los vértices getVertexDegrees()

Para un grafo no dirigido el grado de un vértice es el número de aristas incidentes a ese vértice. Para un grafo dirigido cuentan tanto las aristas entrantes como las salientes. En la Figura vemos como ejecutar esta acción sobre un grafo no dirigido con un autobucle. Se observa el comentario en rojo El grafo es multigrafo y el algoritmo podría no ejecutarse correctamente
, motivo que junto al control forzar dirigido ya explicamos en el apartado anterior y que volveremos a exponer al final de este apartado.
El algoritmo se ejecuta, como en todos los casos, sobre la matriz de adyacencia:
function getVertexDegrees({matrix=[], forceDirected=false}) {
let result = [];
try {
let directed = forceDirected || isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
let n = matrix.length;
for (let i=0; i<n; i++){
let p = 0;
for (let j=0; j<n; j++) {
if (directed && matrix[i][j]!==0 && matrix[j][i]!==0 || i===j && matrix[i][j]!==0) {
p += 2;
} else if (matrix[i][j]!==0 || matrix[j][i]!==0) {
p += 1;
}
}
result.push(p);
}
} catch(e) {result = e.message}
return result;
}El resultado obtenido es un array [4, 3, 2, 3, 3, 1] con los grados de los vértices en el mismo orden que los índices de los nodos.
Time: 0 ms Obtener grados de los vértices: [4,3,2,3,3,1] Índice del array es el índice del nodo, valor del array es el grado del nodo Valor nodo → grado ⇒ 1→4, 2→3, 3→2, 4→3, 5→3, 6→1

En la Figura vemos como la aplicación modifica el aspecto visual del grafo agregando los grados de los vértices en texto de color azul a los valores de los nodos.
1 1 0 0 1 0 1 0 1 0 1 0 0 1 0 1 0 0 0 0 1 0 1 1 1 1 0 1 0 0 0 0 0 1 0 0
Esto no supone modificar la matriz de adyacencia ni siquiera el JSON de salida, solo es una presentación en pantalla como ayuda visual de la ejecución.
{"nodes":[
{"index":0,"nodeOffset":"-22.8 65.2","value":"1","parent":[{"index":-1},{"index":0,"lineType":"cubic","lineOffset":"4 0 0 4"}]},
{"index":1,"nodeOffset":"-16 16.4","value":"2","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-27.2 -33.4","value":"3","parent":[{"index":1}]},
{"index":3,"nodeOffset":"1.6 -53.6","value":"4","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-22 21.2","value":"5","parent":[{"index":0},{"index":1},{"index":3}]},
{"index":5,"nodeOffset":"18 -94.8","value":"6","parent":[{"index":3}]}
],
"config":{
"algorithm":"Get vertex degrees"
}}
En la Figura vemos la ejecución en Wolfram usando la función VertexDegree[g], encontrando más información en Vertex Degree en Wolfram MathWorld. Se obtienen los mismos grados 4, 3, 2, 3, 3, 1.
g = AdjacencyGraph[{{1,1,0,0,1,0},{1,0,1,0,1,0},{0,1,0,1,0,0},{0,0,1,0,1,1},{1,1,0,1,0,0},{0,0,0,1,0,0}}, ImageSize -> 266, VertexSize -> {"Scaled", 0.12},
VertexLabels -> {1 -> Placed[1,Center], 2 -> Placed[2,Center], 3 -> Placed[3,Center], 4 -> Placed[4,Center], 5 -> Placed[5,Center], 6 -> Placed[6,Center]},
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
VertexDegree[g]
Ya vimos el multigrafo con aristas dobles y autobucle de la Figura en el apartado anterior donde aplicábamos el algoritmo para obtener el total de aristas. Para obtener los grados de los nodos pasa lo mismo. Como explicamos en ese apartado y un tema anterior sobre multigrafos y las limitaciones de la matriz de adyacencia, no hay forma de diferenciar con una matriz de adyacencia entre un grafo no dirigido y su equivalente todo dirigido, con o sin autobucles.
0 1 1 1 1 0 1 0 1 1 1 1 1 0 1 0
Si no especificamos algo más, su matriz de adyacencia definirá un grafo no dirigido y no el grafo de la Figura. Para evitarlo usamos el control forzar dirigido, que pasamos al algoritmo como el argumento booleano forceDirected con valor falso por defecto. Activándolo obtenemos el resultado correcto [6, 4, 8, 4] que son las aristas incidentes tanto de entrada como de salida a cada nodo:
Time: 0 ms Obtener grados de los vértices: [6,4,8,4] Índice del array es el índice del nodo, valor del array es el grado del nodo Valor nodo → grado ⇒ 0→6, 1→4, 2→8, 3→4
Estes es el JSON que puede importar en la aplicación.
{"nodes":[
{"index":0,"nodeOffset":"8.17","parent":[{"index":-1},{"index":2},{"index":1,"lineType":"quadratic","lineOffset":"3 -3"},{"index":3,"lineOffset":"-3 -3","lineType":"quadratic"}]},
{"index":1,"nodeOffset":"16 -5","parent":[{"index":0},{"index":2,"lineType":"quadratic","lineOffset":"3 3"}]},
{"index":2,"nodeOffset":"-16.17 40","parent":[{"index":1},{"index":0,"lineOffset":10.37,"lineType":"quadratic"},{"index":3,"lineType":"quadratic","lineOffset":"-2 2"},{"index":2,"lineType":"cubic","lineOffset":"-4 4 4 4"}]},
{"index":3,"nodeOffset":"-24 -55","parent":[{"index":2},{"index":0}]}
],
"config":{
"wv":73,
"hv":77,
"width":182.51,
"height":192.5,
"adjust":false,
"wvIni":73,
"markerEnd":"arrow",
"algorithm":"Get vertex degrees",
"forceDirected":true
}}
Y este es el resultado en Wolfram obteniendo los mismos grados 6, 4, 8, 4.
g = AdjacencyGraph[{{0,1,1,1},{1,0,1,0},{1,1,1,1},{1,0,1,0}}, ImageSize -> 193, VertexSize -> {"Scaled", 0.16},
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center]},
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold],
VertexStyle -> White, DirectedEdges -> True, EdgeStyle -> {{Black,Thickness[0.005]}}];
VertexDegree[g]Obtener grados entrada/salida de los vértices getVertexInOutDegrees()
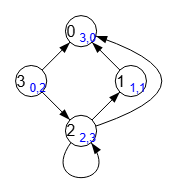
Los grados de un nodo son las aristas que entran y salen de ese nodo, tal como vimos en el apartado anterior, tanto para un grafo dirigido como uno no dirigido. Para un grafo no dirigido podemos definir los grados de entrada o salida, diferenciando entre aristas que entran o salen del nodo. En la Figura vemos un grafo dirigido con autobucle, donde se incluye estos grados. Por ejemplo, para el nodo "0" entran 3 aristas y no sale ninguna indicándose con el subíndice "3,0". El nodo "2" tiene un autobucle y "2" aristas entrantes y "3" salientes, pues el autobucle entra y sale al mismo tiempo.
El resultado es un Array indicando cada pareja de aristas entrantes/salientes para cada nodo correlativamente:
Time: 0 ms Obtener grados entrada/salida de los vértices: [[3,0],[1,1],[2,3],[0,2]]
Puede importar el ejemplo con este JSON:
{"nodes":[
{"index":0,"nodeOffset":"-4","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"16 -5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-4 -10","parent":[{"index":1},{"index":0,"lineOffset":10.37,"lineType":"quadratic"},{"index":2,"lineType":"cubic","lineOffset":"-4 4 4 4"}]},
{"index":3,"nodeOffset":"-24 -55","parent":[{"index":2},{"index":0}]}
],
"config":{
"wv":73,
"hv":77,
"width":182.51,
"height":192.5,
"adjust":false,
"wvIni":73,
"markerEnd":"arrow",
"algorithm":"Get vertex in/out degrees"
}}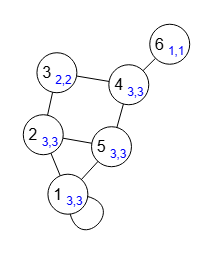
Es obvio que si se aplica a un grafo dirigido cada nodo tiene las mismas aristas entrantes que salientes. En la Figura vemos un grafo no dirigido, donde cada nodo tiene igual aristas de entrada que salida. Se obtiene el siguiente resultado, donde vemos que cuando los valores de los nodos son distintos de los índices la aplicación traduce esos valores, por ejemplo para el nodo con índice "0" expone 1 → [3,3] y así sucesivamente.
Observe que el autobucle es arista entrante y saliente al mismo tiempo.
Time: 1 ms Obtener grados entrada/salida de los vértices: [[3,3],[3,3],[2,2],[3,3],[3,3],[1,1]] Valor nodo → [grado entrada, grado salida] ⇒ 1 → [3,3], 2 → [3,3], 3 → [2,2], 4 → [3,3], 5 → [3,3], 6 → [1,1]
Se puede importar con este JSON. Hemos ampliado a 8 el radio de los nodos con nodeRadius para dar sitio a los subíndices (el valor base es 6.25)
{"nodes":[
{"index":0,"nodeOffset":"-22.8 65.2","value":"1","parent":[{"index":-1},{"index":0,"lineType":"cubic","lineOffset":"4 0 0 4"}]},
{"index":1,"nodeOffset":"-16 16.4","value":"2","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-27.2 -33.4","value":"3","parent":[{"index":1}]},
{"index":3,"nodeOffset":"1.6 -53.6","value":"4","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-22 21.2","value":"5","parent":[{"index":0},{"index":1},{"index":3}]},
{"index":5,"nodeOffset":"18 -94.8","value":"6","parent":[{"index":3}]}
],
"config":{
"nodeRadius":8,
"algorithm":"Get vertex in/out degrees"
}}Este es el JavaScript para ejecutar getVertexInOutDegrees():
function getVertexInOutDegrees({matrix=[]}){
let result = [];
try {
let n = matrix.length;
for (let i=0; i<n; i++){
let p = [0, 0];
for (let j=0; j<n; j++) {
if (matrix[i][j]!==0) {
p[1] += 1;
}
if (matrix[j][i]!==0) {
p[0] += 1;
}
}
result.push(p);
}
} catch(e) {result = e.message}
return result;
}Tiene ciclos hasCycles()

El algoritmo para saber si un grafo tiene ciclos (hasCycles()) se aplica en la aplicación como se muestra en la Figura. Recibe la matriz de adyacencia y el argumento ignorar autobucles (ignoreSelfLoops) que por defecto es falso y que explicaremos más abajo.
La función JavaScript hasCycles({matrix=[], ignoreSelfLoops=false}) se expone a continuación:
function hasCycles({matrix=[], ignoreSelfLoops=false}){
let result = false;
try {
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
let cycles = getCyclesAll({matrix, directed, firstMatch: true, ignoreSelfLoops});
if (typeof cycles==="string") throw new Error(cycles);
result = cycles.length>0;
} catch(e){result = e.message}
return result;
}Usa getCyclesAll() que veremos en un siguiente apartado para encontrar todos los ciclos, con el argumento firstMatch: true de tal forma que cuando encuentre el primer ciclo finaliza, así que si tiene ciclos devolverá un resultado con al menos un ciclo convirtiendo cycles.length>0 en verdadero.
Y también isGraphDirected() para saber si el grafo es dirigido que ya vimos en un tema anterior.

En la Figura vemos el grafo de ejemplo que contiene un autobucle, muestra que puede importar desde la colección que se abre con el botón con icono o bien copiar desde el siguiente JSON.
El resultado es un booleano con valor verdadero para este ejemplo:
Time: 0 ms Tiene ciclos: true
{"nodes":[
{"index":0,"nodeOffset":"-22.8 65.2","value":"1","parent":[{"index":-1},{"index":0,"lineType":"cubic","lineOffset":"4 0 0 4"}]},
{"index":1,"nodeOffset":"-16 16.4","value":"2","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-27.2 -33.4","value":"3","parent":[{"index":1}]},
{"index":3,"nodeOffset":"1.6 -53.6","value":"4","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-22 21.2","value":"5","parent":[{"index":0},{"index":1},{"index":3}]},
{"index":5,"nodeOffset":"18 -94.8","value":"6","parent":[{"index":3}]}
],
"config":{
"algorithm":"Has cycles"
}}
En la Figura vemos la ejecución en Wolfram con la función FindCycle[g], que devuelve una lista de ciclos. Para saber si tiene ciclos hacemos Length[FindCycle[g]]>0 devolviendo un booleano en caso de que la longitud de ciclos encontrados sea mayor que cero.
g = AdjacencyGraph[{{1,1,0,0,1,0},{1,0,1,0,1,0},{0,1,0,1,0,0},{0,0,1,0,1,1},{1,1,0,1,0,0},{0,0,0,1,0,0}},
ImageSize -> 266, VertexSize -> {"Scaled", 0.12}, VertexLabels -> {1 -> Placed[1,Center], 2 -> Placed[2,Center],
3 -> Placed[3,Center], 4 -> Placed[4,Center], 5 -> Placed[5,Center], 6 -> Placed[6,Center]},
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold],
VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
Length[FindCycle[g]]>0
Si eliminamos las aristas "2-5" y "3-4" en el grafo anterior llegamos al grafo de la Figura. La ejecución de tiene ciclos resultará verdadero si ignorar autobucles es falso pues detecta el autobucle como un ciclo. Si se ignoran autobucles resultará falso pues no hay otros ciclos que el del autobucle.
{"nodes":[
{"index":0,"nodeOffset":"-6.13 65.2","value":"1","parent":[{"index":-1},{"index":0,"lineType":"cubic","lineOffset":"4 0 0 4"}]},
{"index":1,"nodeOffset":"-7.67 16.4","value":"2","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-27.2 -33.4","value":"3","parent":[{"index":1}]},
{"index":3,"nodeOffset":"-15.07 21.4","value":"4","parent":[{"index":-1}]},
{"index":4,"nodeOffset":"-5.33 21.2","value":"5","parent":[{"index":0},{"index":3}]},
{"index":5,"nodeOffset":"-7 -19.8","value":"6","parent":[{"index":3}]}
],
"config":{
"algorithm":"Has cycles",
"ignoreSelfLoops":true
}}
En la Figura vemos como se ejecuta en Wolfram, que siempre ignora los autobucles, pues no los considera ciclos.

Para obtener el grafo anterior hemos reducido el tamaño de los vértices con el factor 0.85 como se observa en la Figura, con la finalidad de que el autobucle se muestre más claramente.
g = AdjacencyGraph[{{1,1,0,0,1,0},{1,0,1,0,0,0},{0,1,0,0,0,0},{0,0,0,0,1,1},{1,0,0,1,0,0},{0,0,0,1,0,0}},
ImageSize -> 266, VertexSize -> {"Scaled", 0.1}, VertexLabels -> {1 -> Placed[1,Center], 2->Placed[2,Center],
3->Placed[3,Center], 4->Placed[4,Center], 5->Placed[5,Center], 6->Placed[6,Center]},
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White,
EdgeStyle->{{Black,Thickness[0.005]}}];
Length[FindCycle[g]]>0

El grafo dirigido de la Figura no tiene ciclos si ignoramos los autobucles como se muestra en la Figura. En otro caso sólo tiene el ciclo del autobucle.
{"nodes":[
{"index":0,"nodeOffset":"-4","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"16 -5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-4 -10","parent":[{"index":1},{"index":0,"lineOffset":10.37,"lineType":"quadratic"},{"index":2,"lineType":"cubic","lineOffset":"-4 4 4 4"}]},
{"index":3,"nodeOffset":"-24 -55","parent":[{"index":2},{"index":0}]}
],
"config":{
"wv":73,
"hv":77,
"width":182.51,
"height":192.5,
"adjust":false,
"wvIni":73,
"markerEnd":"arrow",
"algorithm":"Has cycles",
"ignoreSelfLoops":true
}}
En la Figura al inicio de este apartado veíamos que la aplicación exponía el aviso El grafo es multigrafo y el algoritmo podría no ejecutarse correctamente
. El motivo ya lo explicamos en el apartado multigrafos y las limitaciones de la matriz de adyacencia de un tema anterior. El grafo de la Figura es un multigrafo no dirigido con múltiples aristas que no es representable en la matriz de adyacencia. Visualmente se observan varios ciclos posibles entre los dos nodos, pero el algoritmo nos dirá que no tiene ciclos.
0 1 1 0
Exportando su matriz de adyacencia sólo presenta una de las cuatro aristas del grafo. Y en un grafo con dos nodos y una arista entre ellos no hay ciclos, obviamente.
{"nodes":[
{"index":0,"nodeOffset":"-28.67 6.8","parent":[{"index":-1},{"index":1},{"index":1,"lineType":"cubic","lineOffset":"2 -2 0 -2"}]},
{"index":1,"nodeOffset":"35.34 -18.2","parent":[{"index":0,"lineOffset":"0 1.47"},{"index":0,"lineType":"cubic","lineOffset":"2 2 0 2"}]}
],
"config":{
"algorithm":"Has cycles"
}}Obtener ciclos desde nodo getCyclesFromNode()

En la Figura vemos como obtener todos los ciclos desde el nodo con valor "1" (índice 0). El primer ciclo encontrado es el autobucle. Después veremos que Wolfram ignora los autobucles, pero en la aplicación sí los consideramos. La ejecución del algoritmo no modifica la matriz de adyacencia del grafo, resaltando los caminos de cada ciclo usando las opciones color camino y color fondo nodo, pudiendo iterar por los ciclos encontrados con los botones que se observa en la parte superior derecha de la Figura. Devuelve el resultado siguiente:
Time: 0 ms Obtener ciclos desde nodo: [[0,0],[0,1,2,3,4,0],[0,1,4,0]] Cada subarray es un ciclo que incluye índices de nodos Valores de nodos de ciclos desde el nodo "1" (index 0) ⇒ [1, 1], [1, 2, 3, 4, 5, 1], [1, 2, 5, 1]
Con este JSON puede importar el grafo:
{"nodes":[
{"index":0,"nodeOffset":"-22.8 65.2","value":"1","parent":[{"index":-1},{"index":0,"lineType":"cubic","lineOffset":"4 0 0 4"}]},
{"index":1,"nodeOffset":"-16 16.4","value":"2","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-27.2 -33.4","value":"3","parent":[{"index":1}]},
{"index":3,"nodeOffset":"1.6 -53.6","value":"4","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-22 21.2","value":"5","parent":[{"index":0},{"index":1},{"index":3}]},
{"index":5,"nodeOffset":"18 -94.8","value":"6","parent":[{"index":3}]}
],
"config":{
"algorithm":"Get cycles from node"
}}
En la Figura realizamos una composición con todos los ciclos encontrados con índices [[0,0],[0,1,2,3,4,0],[0,1,4,0]] o con valores [1, 1], [1, 2, 3, 4, 5, 1], [1, 2, 5, 1]. Un camino es una lista de nodos con una arista entre cada dos nodos. Si el primero es igual que el último será un ciclo.
Se resaltan los caminos en cada subgrafo, usando las opciones color camino y color fondo nodo que puede observar en la Figura.
Si en la aplicación hubiésemos marcado ignorar autobucles veríamos que omitiría el primer autociclo.

Como Wolfram no reconoce los autobucles como ciclos, en la Figura vemos los otros dos subgrafos coincidentes con los ciclos desde el nodo con valor "1" (índice 0) que obtuvimos en la aplicación.
Usa la función FindCycle[{g, 1}, Infinity, All]. El primer argumento {g, 1} busca los ciclos en el grafo g desde el nodo "1". El segundo argumento Infinity busca ciclos de cualquier longitud. Ahí se podría filtrar con un valor numérico k con lo que filtraría ciclos hasta esa longitud. Con {k} filtraría exactamente de esa longitud. El tercer argumento All devuelve todos los ciclos, pudiendo filtrar hasta un valor si se incluye un número. Estas opciones de filtrado no están disponibles en nuestra aplicación.
Para presentar todos los ciclos usamos la función HighlightGraph[] para resaltar una lista de aristas dentro de un grafo y Table[] para iterar por todos los subgfrafos.
g = AdjacencyGraph[{{1,1,0,0,1,0},{1,0,1,0,1,0},{0,1,0,1,0,0},{0,0,1,0,1,1},{1,1,0,1,0,0},{0,0,0,1,0,0}},
ImageSize->266, VertexSize->{"Scaled", 0.12}, VertexLabels->{1->Placed[1,Center], 2->Placed[2,Center],
3->Placed[3,Center], 4->Placed[4,Center], 5->Placed[5,Center], 6->Placed[6,Center]},
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}]
h = FindCycle[{g, 1}, Infinity, All]
Table[HighlightGraph[g, {Style[EdgeList[i], Red, Thick], Annotation[EdgeList[i], EdgeLabelStyle->Directive[Blue,17.5,Bold]]}], {i, h}]
Veamos ahora el grafo dirigido de la Figura, multigrafo con múltiples aristas, mostrándose todos los ciclos desde el nodo "0", obteniéndose el siguiente resultado.
Time: 0 ms Obtener ciclos desde nodo: [[0,3,0],[0,3,2,0],[0,3,2,1,0]]
{"nodes":[
{"index":0,"nodeOffset":"8.17","parent":[{"index":-1},{"index":3,"lineType":"quadratic","lineOffset":"-2 -2"}]},
{"index":1,"nodeOffset":"16 -5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-4 -10","parent":[{"index":1},{"index":0,"lineOffset":10.37,"lineType":"quadratic"},{"index":3}]},
{"index":3,"nodeOffset":"-36.17 20","parent":[{"index":2,"lineOffset":"-2 2","lineType":"quadratic"},{"index":0}]}
],
"config":{
"wv":73,
"hv":77,
"width":182.51,
"height":192.5,
"adjust":false,
"wvIni":73,
"markerEnd":"arrow",
"algorithm":"Get cycles from node"
}}
En la Figura vemos que Wolfram encuentra los mismos ciclos.
g = AdjacencyGraph[{{0,0,0,1},{1,0,0,0},{1,1,0,1},{1,0,1,0}}, ImageSize->193,
VertexSize->{"Scaled", 0.16}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center]}, VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}]
h = FindCycle[{g, 1}, Infinity, All]
Table[HighlightGraph[g, {Style[EdgeList[i], Red, Thick], Annotation[EdgeList[i], EdgeLabelStyle->Directive[Blue,17.5,Bold]]}], {i, h}]Veamos el código JavaScript de la función getCyclesFromNode(). Usa isGraphDirected() para saber si el grafo es dirigido que ya vimos en un tema anterior. Se van obteniendo ciclos con getCyclesIndex(), se ordenan y se comprueban si no existen previamente en el resultado.
function getCyclesFromNode({matrix=[], index=0, directed=null, ignoreSelfLoops=false}){
let result = [];
try {
let n = matrix.length;
if (directed===null) {
directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
}
let cycles = getCyclesIndex({matrix, index, directed, ignoreSelfLoops});
if (typeof cycles==="string") throw new Error(cycles);
if (cycles.hasOwnProperty("warning")) result.warning = cycles.warning;
for (let cycle of cycles) {
cycle = sortCycle(cycle, index);
if (!includesCycle(result, cycle)) {
result.push([...cycle]);
}
}
result.forEach(v => v.push(v[0]));
} catch(e){result = e.message}
return result;
}La función que realmente busca los ciclos desde un índice index es getCyclesIndex(). Es un recursivo que finalizará con el primer ciclo encontrado si el argumento firstMatch es verdadero. En otro caso seguirá hasta devolverlos todos. O bien si se llega al máximo de iteraciones finalizará, anotando en la propiedad cycles.warning un aviso al respecto.
function getCyclesIndex({matrix=[], index=0, directed=null, firstMatch=false, ignoreSelfLoops=false, cycle=[], cycles=[]}){
try {
if (iter++, iter>maxIter) {
cycles.warning = `Maximum iterations ${maxIter} reached`;
} else {
if (directed===null) {
directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
}
if (cycle.includes(index)){
let bool = !directed && cycle.length>=3 || directed && cycle.length>=2 || !ignoreSelfLoops && cycle.length<2;
if (bool && cycle[0]===index) {
cycles.push(cycle);
}
} else if (!firstMatch || cycles.length===0) {
let parents = getParents({matrix, index});
if (parents.length>0) {
let copyCycle = [...cycle, index];
for (let i of parents) {
let temp = getCyclesIndex({matrix, index:i, directed, firstMatch, ignoreSelfLoops, cycle:copyCycle, cycles});
}
}
}
}
} catch(e){cycles = e.message}
return cycles;
}La función auxiliar sortCycle() ordena los ciclos poniendo al inicio el índice min:
function sortCycle(cycle=[], min=null){
if (cycle.length>0) {
if (min===null) min = Math.min(...cycle);
while (iter++, iter<=maxIter && cycle[0]!==min) {
cycle.unshift(cycle.pop());
}
}
return cycle;
}La otra función auxiliar que necesitamos es para comprobar si un ciclo existe ya en la lista de ciclos. Para ello es necesario irlos guardando ordenados.
function includesCycle(cycles=[], cycle=[]) {
if (cycles.length===0 || cycle.length>1 || !Array.isArray(cycle)) return false;
let j = cycle.join(",");
let jr = [...cycle.slice(1), cycle[0]].reverse().join(",");
for (let cy of cycles) {
let k = cy.join(",");
if (j===k || jr===k) return true;
}
return false;
}Obtener todos los ciclos getCyclesAll()

En la Figura vemos como obtener todos los ciclos de un grafo dirigdo. La ejecución del algoritmo no modifica la matriz de adyacencia del grafo, resaltando los caminos de cada ciclo usando las opciones color camino y color fondo nodo, pudiendo iterar por los ciclos encontrados con los botones que se observa en la parte superior derecha de la Figura. Devuelve el resultado siguiente:
Time: 0 ms Obtener todos los ciclos: [[0,4,1,0],[0,4,2,0],[0,4,2,1,0]] Cada subarray es un ciclo que incluye índices de nodos Valores de nodos de todos los ciclos ⇒ [0, 4, X, 0], [0, 4, 2, 0], [0, 4, 2, X, 0]
Este es el JSON para importar en la aplicación:
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"value":"X","parent":[{"index":0,"value":"A"}]},
{"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"C"}]},
{"index":3,"parent":[{"index":1,"value":"D","lineTextOffset":"-0.75 0.25"},{"index":4,"value":"E"}]},
{"index":4,"parent":[{"index":1,"value":"F"},{"index":2},{"index":0,"lineOffset":"1","markerReverse":true,"value":"G"}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Get cycles all"
}}
En la Figura componemos los tres subgrafos con los ciclos [[0,4,1,0],[0,4,2,0],[0,4,2,1,0]], relacionados por índices de nodos. O bien [0, 4, X, 0], [0, 4, 2, 0], [0, 4, 2, X, 0] si usamos sus valores.

En la Figura vemos el resultado en Wolfram, equivalente al nuestro.
Usa la función FindCycle[g, Infinity, All]. El primer argumento {g, n} busca los ciclos en el grafo g desde el nodo n. Si se omite busca todos los ciclos. El segundo argumento Infinity busca ciclos de cualquier longitud. Ahí se podría filtrar con un valor numérico k con lo que filtraría ciclos hasta esa longitud. Con {k} filtraría exactamente de esa longitud. El tercer argumento All devuelve todos los ciclos, pudiendo filtrar hasta un valor si se incluye un número. Estas opciones de filtrado no están disponibles en nuestra aplicación.
Para presentar todos los ciclos usamos la función HighlightGraph[] para resaltar una lista de aristas dentro de un grafo y Table[] para iterar por todos los subgrafos.
g = AdjacencyGraph[{{0,0,0,0,1},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}}, ImageSize->188,
VertexSize->{"Scaled", 0.17}, VertexLabels->{1->Placed[0,Center], 2->Placed["X",Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(2->1)->"A", (3->1)->"B", (3->2)->"C", (4->2)->"D", (4->5)->"E", (5->2)->"F", (1->5)->"G"}, VertexStyle->White,
DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}]
h = FindCycle[g, Infinity, All]
Table[HighlightGraph[g, {Style[EdgeList[i], Red, Thick], Annotation[EdgeList[i], EdgeLabelStyle->Directive[Blue,17.5,Bold]]}], {i, h}]
En caso de alcanzarse el máximo de iteraciones (10000 por defecto), el algoritmo finalizará con los ciclos encontrados, exponiendo el mensaje Máximas iteraciones 10000 alcanzadas. Es posible que no se hayan obtenido todos los resultados
, como se observa en la Figura.
El código JavaScript para obtener todos los ciclos es getCyclesAll(). Usa isGraphDirected() para saber si el grafo es dirigido que ya vimos en un tema anterior. Y las funciones auxiliares getCyclesIndex(), sortCycle() y includesCycle() que ya vimos en el apartado anterior. Con el argumento firstMatch devuelve el primer ciclo encontrado, lo que nos sirve para comprobar si un grafo tiene ciclos sin necesidad de recuperarlos todos. En esto se basa el algoritmo hasCycles() que vimos en un apartado anterior.
function getCyclesAll({matrix=[], firstMatch=false, directed=null, ignoreSelfLoops=false}) {
let result = [];
try {
let n = matrix.length;
if (directed===null) {
directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
}
for (let index=0; index<n; index++) {
let cycles = getCyclesIndex({matrix, index, directed, firstMatch, ignoreSelfLoops});
if (typeof cycles==="string") throw new Error(cycles);
if (cycles.hasOwnProperty("warning")) result.warning = cycles.warning;
for (let cycle of cycles) {
cycle = sortCycle(cycle);
if (!includesCycle(result, cycle)) {
result.push([...cycle]);
}
}
if (cycles.length>0 && firstMatch) break;
}
result.forEach(v => v.push(v[0]));
} catch(e){result = e.message}
return result;
}