Direccionalidad en grafos
Cambiar direccionalidad: dirigido arriba/abajo, no dirigido y todo dirigido

He agregado a Grafos SVG un nuevo botón para cambiar la dirección del grafo de una forma más simple. En la Figura podemos ver el panel para cambiar la dirección, entre dirigido arriba, dirigido abajo, no dirigido y todo dirigido que veremos en este apartado. En un apartado siguiente veremos todo arriba, todo abajo, doble flecha e inverso.
Si i, j son dos índices de nodos con j > i, si la mitad o más de las aristas son j🡒i lo denominamos grafo dirigido arriba. Si menos de la mitad son j < i tendremos i🡒j y lo denominamos dirigido abajo.

También podemos decir que un grafo es dirigido arriba si la mitad o más aristas van de un nodo con índice mayor que el índice del nodo de destino, como es el caso del grafo de la Figura. En otro caso será dirigido abajo.
Esta convención se basa en la ubicación automática de nodos usando niveles que expusimos en el tema anterior, pues para una relación dirigido arriba entre dos nodos significa que se ubican los nodos apuntados (padres) en el mismo nivel o por encima de los que les apuntan (hijos), como son las aristas 1🡒0, 2🡒0, 2🡒1, 3🡒1, 4🡒1 y 4🡒2 de la Figura. Mientras que las aristas 3🡒4 y 0🡒4 son relaciones dirigido abajo, donde el nodo apuntando está en el mismo nivel o por debajo del nodo que le apunta. Como la mayor parte de las aristas son dirigidas arriba, el grafo se define dirigido arriba.
Observe que el nodo "0" no apunta a ningún nodo superior, es decir, no hay ningun nodo con índice menor al que apunte, pues su enlace es 0🡒4 con índice "4" mayor, ubicándose entonces al inicio como nodo raíz con padre {"index":-1}. Mientras que el nodo "3" no tienen nadie que le apunte, por lo que podríamos denominarlo como hoja, lo cual es correcto para un árbol aunque este grafo no lo sea.
0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1 0 0
Para este apartado empezamos usando el grafo de muestra de la Figura, que puede importar en la aplicación desde esta matriz de adyacencia en formato SSV o, indistintamente, desde el siguiente JSON:
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1},{"index":4}]},
{"index":4,"parent":[{"index":1},{"index":2}]}
],
"config":{
"markerEnd":"arrow"
}}Si seleccionamos una arista cambiaremos la dirección de esa arista. Si no hay ninguna seleccionada se cambiarán las direcciones de todas las aristas. En lo que sigue vemos ejemplos para cambiar todas las aristas.

En la Figura he compuesto en una misma imagen las primeras cuatro direccionalidades del grafo que vamos a explicar. Las matrices de adyacencia se presentan en formato SSV (valores separados por espacios). La primera es para el dirigido arriba que es el grafo inicial, no produciéndose ningún cambio:
0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1 0 0
Y a continuación el dirigido abajo:
0 1 1 0 0 0 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0
Vea que el dirigido arriba tiene la mayor parte de las aristas con valor distinto de cero por debajo de la diagonal de la matriz. Mientras que el dirigido abajo es al revés.
Además una es la transposición de la otra, intercambiando filas por columnas. El objeto nodes del JSON es exactamente el mismo, solo cambia la propiedad "markerStart":"arrow" cuando en el dirigido arriba era "markerEnd":"arrow"
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1},{"index":4}]},
{"index":4,"parent":[{"index":1},{"index":2}]}
],
"config":{
"markerStart":"arrow"
}}0 1 1 0 1 1 0 1 1 1 1 1 0 0 1 0 1 0 0 1 1 1 1 1 0
El siguiente es el no dirigido, con una matriz simétrica con respecto a la diagonal. Tiene el mismo objeto nodes en el JSON, donde ahora no aparece "markerStart" ni "markerEnd", lo que significa que tienen el valor "none".
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1},{"index":4}]},
{"index":4,"parent":[{"index":1},{"index":2}]}
],
"config":{
}}0 1 1 0 1 1 0 1 1 1 1 1 0 0 1 0 1 0 0 1 1 1 1 1 0
Y por último el todo dirigido, que también podemos denominar como arista doble por el motivo que veremos después, cuya matriz es exactamente igual que el no dirigido, diferenciándose solo por la configuración "markerEnd":"arrow":
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4},{"index":1},{"index":2}],"nodeOffset":"25 0"},
{"index":1,"parent":[{"index":0},{"index":2},{"index":3},{"index":4}]},
{"index":2,"parent":[{"index":0},{"index":1},{"index":4}]},
{"index":3,"parent":[{"index":1},{"index":4}],"nodeOffset":"-16.67 50"},
{"index":4,"parent":[{"index":1},{"index":2},{"index":0},{"index":3}],"nodeOffset":"-8.33 50"}
],
"config":{
"markerEnd":"arrow"
}}Este punto es muy importante, pues no es posible representar solo con una matriz un grafo con todas las aristas dirigidas en ambos sentidos. Si no todas las aristas son dirigidas, si es posible. Veamos esto.

En la Figura hemos agregado una arista doble (o toda dirigida) entre los nodos "3" y "4". Esta es la matriz de adyacencia:
0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1 1 0
En esta matriz observamos el 1 con borde en la quinta fila del nodo "4", valor que se agrega en la posición del nodo "3" en esa fila, con lo que tenemos la arista "4🡒3". En la cuarta fila del nodo "3" tenemos otro 1 recuadrado en la posición del nodo "4", con lo que tenemos la arista "3🡒4". Vemos que ambos recuadros son simétricos respecto a la diagonal. Obviamente, si todos los nodos son simétricos, entonces es una matriz simétrica y el grafo se convierte en no dirigido, desapareciendo todas las flechas.
operateDirectionGraph() expondremos una forma de representar un grafo todo dirigido en una matriz de adyacencia modificada.
Vea que las arista doble "3⟷4" o "4⟷3" son realmente dos aristas "4🡒3" y "3🡒4" en un grafo dirigido, como se observa en la Figura desplazando una de ellas. Este es el JSON de ese grafo:
{"nodes":[ {"index":0,"parent":[{"index":-1},{"index":4}]}, {"index":1,"parent":[{"index":0}]}, {"index":2,"parent":[{"index":0},{"index":1}]}, {"index":3,"parent":[{"index":1},{"index":4,"lineOffset":"0 1.15"}]}, {"index":4,"parent":[{"index":1},{"index":2},{"index":3}]} ], "config":{ "markerEnd":"arrow" }}La arista doble o toda dirigida son dos aristas, una en cada sentido. Y no debe confundirse con la arista con doble flecha que veremos en el siguiente apartado, que es una única arista con una flecha en cada punta de la arista.
Cambiar direccionalidad: grafos acíclicos, aristas con doble flecha e inversión de aristas

Veamos ahora las otras opciones de cambios de dirección que aún no hemos visto: todo arriba, todo abajo, doble flecha e inverso, como se observa en la Figura.
0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 1 1 0
Con la dirección todo arriba todas las aristas van arriba, de tal forma que si i<j las aristas son j🡒i. Se observa en la matriz que los valores en y por encima de la diagonal son todos cero.
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1}]},
{"index":4,"parent":[{"index":1},{"index":2},{"index":0},{"index":3}]}
],
"config":{
"markerEnd":"arrow"
}}0 1 1 0 1 0 0 1 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0
Con la dirección todo abajo todas las aristas van abajo, de tal forma que si i<j las aristas son i🡒j. Se observa en la matriz que los valores en y por debajo de la diagonal son todos cero. Con estas dos opciones todo arriba o todo abajo convertimos el grafo en acíclico, puesto que al ir todas las aristas en una única dirección no hay posibilidad de ciclos.
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4}]},
{"index":1,"parent":[{"index":0,"markerStart":"arrow","markerEnd":"none"}]},
{"index":2,"parent":[{"index":0,"markerStart":"arrow","markerEnd":"none"},{"index":1,"markerStart":"arrow","markerEnd":"none"}]},
{"index":3,"parent":[{"index":1,"markerStart":"arrow","markerEnd":"none"},{"index":4}]},
{"index":4,"parent":[{"index":1,"markerStart":"arrow","markerEnd":"none"},{"index":2,"markerStart":"arrow","markerEnd":"none"}]}
],
"config":{
"markerEnd":"arrow"
}}0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1 0 0
Con la dirección doble flecha la matriz no cambia, es la misma que la inicial. Para cada arista se incluye una doble flecha con "markerStart":"arrow" y "markerEnd":"arrow". Esto es diferente que la dirección todo dirigido como veíamos más arriba, donde aparecían dos aristas en ambos sentidos entre ambos nodos. En este caso es una única arista con una flecha al principio y otra al final, por lo que no es representable su matriz de adyacencia.
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1},{"index":4}]},
{"index":4,"parent":[{"index":1},{"index":2}]}
],
"config":{
"markerStart":"arrow",
"markerEnd":"arrow"
}}
Por último veamos la dirección inverso. Tomando el grafo de la Figura con aristas "4🡒3" y "3🡒4", al aplicar dirección inversa, invierte todas las aristas.
0 1 1 0 0 0 0 1 1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 1 0
La matriz no cambia. El JSON sólo se diferencia que antes había "markerEnd":"arrow" en la configuración y ahora tenemos "markerStart":"arrow".
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1},{"index":4,"lineOffset":"0 1.15"}]},
{"index":4,"parent":[{"index":1},{"index":2},{"index":3}]}
],
"config":{
"markerStart":"arrow"
}}
Tomando el grafo de la derecha de la Figura, aplicamos la arista "0-1" como no dirigida y la "1⟷3" con arista con doble flecha. Como vimos antes, una arista doble flecha es un única línea con una flecha al principio y otra al final de la línea, algo diferente como la relación todo dirigido entre dos nodos, que también puede denominarse arista doble pues son dos aristas en los dos sentidos, como el caso de "3🡒4" y "4🡒3" en ese grafo.
Lo que obtenemos, un grafo con mezcla de direcciones, es el primer grafo de los compuestos en la Figura, con esta matriz de adyacencia:
0 1 1 0 0 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 1 0 0 1 0
Esta matriz de adyacencia no representa el grafo, pues al mezclar aristas dirigidas con no dirigidas y doble flecha, no podemos obtener su representación en la matriz de adyacencia. Si usamos esta matriz para obtener su grafo, vemos el segundo a la derecha en la Figura. La arista doble flecha "1⟷3" pierde esa condición y se convierte en una arista simple "3🡒1". La arista no dirigida "0-1" se convierte en todo dirigido o arista doble, con dos aristas "0🡒1" y "1🡒0", lo que podemos comprobar separando esa arista y las ya existentes "3🡒4" y "4🡒3" que no se ven afectadas, tal como se observa en el grafo inferior de la Figura.
Ajustes visuales: intercambiar enlaces

La acción intercambiar enlaces estaba en la aplicación anterior como un opción de entrada y ahora la he traspasado a ajustes visuales (enlaces), que se abre con el botón que ya expusimos en un tema anterior. Con la acción enlaces podemos eliminar la propiedad quitar marcador invertido (markerReverse) o intercambiar enlaces, como vemos en la Figura.

El JSON del grafo que podemos importar para este apartado es el que expone a continuación, donde vemos "markerEnd":"arrow" ubicándose la flecha al final de cada enlace. Así por ejemplo, 1🡒0 tiene la flecha apuntando al nodo "0".
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4}]},
{"index":1,"parent":[{"index":0}]},
{"index":2,"parent":[{"index":0},{"index":1}]},
{"index":3,"parent":[{"index":1},{"index":4}]},
{"index":4,"parent":[{"index":1},{"index":2}]}
],
"config":{
"markerEnd":"arrow"
}}
En la Figura vemos el resultado obtenido tras aplicar intercambiar enlaces, donde el nodo "3" pasa a ser el raíz.
El JSON resultante es el que se expone a continuación, observando que se modifican los parent de los nodos, manteniendo la misma configuración.
{"nodes":[
{"index":0,"parent":[{"index":2},{"index":1}]},
{"index":1,"parent":[{"index":4},{"index":3},{"index":2}]},
{"index":2,"parent":[{"index":4}]},
{"index":3,"parent":[{"index":-1}]},
{"index":4,"parent":[{"index":3},{"index":0}]}
],
"config":{
"markerStart":"arrow"
}}Muestra inicial 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1 0 0 Enlaces intercambiados 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1 0 0
Como todos los ajustes visuales, intercambiar enlaces NO transpone la matriz de adyacencia. Si quisiéramos transponerla podemos usar la acción cambiar la direccionalidad del grafo que veremos en el siguiente apartado. O usar la operación transponer grafo que ejecuta la función operateTransposeGraph() que veremos en un apartado más abajo.
Comparar intercambiar enlaces con cambiar la direccionalidad

En un apartado anterior vimos como intercambiar enlaces no cambiaba la direccionalidad del grafo, es decir, mantenía la misma matriz de adyacencia, pero cambiaba el aspecto visual ubicando los nodos en otras posiciones. Acabamos de ver como cambiar la direccionalidad del grafo, modificándose en este caso la matriz de adyacencia con un aspecto visual que difería del inicial solo en la dirección de las flechas, pues mantenía la estructura del JSON nodes y solo actuaba sobre config.
Antes de ver otras formas de actuar sobre las direcciones, comparemos ambas posibilidades con un nuevo grafo de muestra que vemos en la Figura con una arista curva y un autobucle, donde todos los nodos están posicionados con el ajuste visual ajustar a círculo, ubicándose sobre un círculo en el orden de las agujas del reloj, tal como vemos en su siguiente JSON con las propiedades "nodeOffset" en cada nodo:
{"nodes":[
{"index":0,"nodeOffset":"-4","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"16 -5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-4 -10","parent":[{"index":1},
{"index":0,"lineOffset":10.37,"lineType":"quadratic"},
{"index":2,"lineType":"cubic","lineOffset":"-4 4 4 4"}]},
{"index":3,"nodeOffset":"-24 -55","parent":[{"index":2},{"index":0}]}
],
"config":{
"wv":73,
"hv":77,
"width":182.51,
"height":192.5,
"adjust":false,
"wvIni":73,
"markerEnd":"arrow"
}}
0 0 0 0
1 0 0 0
1 1 1 0
1 0 1 0
La opción para cambiar la dirección del grafo a dirigido abajo accediendo con el botón actúa solo sobre las flechas, cambiando en la configuración "markerStart":"arrow" cuando inicialmente era "markerEnd":"arrow". Mantiene por lo tanto la ubicación anterior de los nodos, pero transpone la matriz de adyacencia cambiando filas por columnas.
Este es el JSON obtenido, con la matriz transpuesta a continuación.
{"nodes":[
{"index":0,"nodeOffset":"-4","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"16 -5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"-4 -10","parent":[{"index":1},
{"index":0,"lineOffset":10.37,"lineType":"quadratic"},
{"index":2,"lineType":"cubic","lineOffset":"-4 4 4 4"}]},
{"index":3,"nodeOffset":"-24 -55","parent":[{"index":2},{"index":0}]}
],
"config":{
"wv":73,
"hv":77,
"width":182.51,
"height":192.5,
"adjust":false,
"wvIni":73,
"markerStart":"arrow"
}}
0 1 1 1
0 0 1 0
0 0 1 1
0 0 0 0
La opción para intercambiar enlaces, ajuste visual al que se puede acceder con el botón , produce el resultado que vemos en la Figura. Como es un ajuste visual, no cambia la direccionalidad del grafo, es decir, no se modifica la matriz de adyacencia. Pero al cambiar los enlaces y estar los nodos posicionados con nodeOffset, la ubicación final parece más errática.
{"nodes":[
{"index":0,"nodeOffset":"-4","parent":[{"index":3},
{"index":2,"lineOffset":10.37,"lineType":"quadratic"},{"index":1}]},
{"index":1,"nodeOffset":"16 -5","parent":[{"index":2}]},
{"index":2,"nodeOffset":"-4 -10","parent":[{"index":3},
{"index":2,"lineType":"cubic","lineOffset":"-4 4 4 4"}]},
{"index":3,"nodeOffset":"-24 -55","parent":[{"index":-1}]}
],
"config":{
"wv":73,
"hv":77,
"width":182.51,
"height":192.5,
"adjust":false,
"wvIni":73,
"markerStart":"arrow"
}}
0 0 0 0
1 0 0 0
1 1 1 0
1 0 1 0Operar sobre la dirección del grafo con operateDirectionGraph()

El panel asistente generación al que se accede con el botón permite realizar operaciones sobre la matriz de adyacencia de un grafo, así como generar nuevas matrices de adyacencia para crear nuevos grafos.
En un tema posterior explicaremos con más detalle lo que contiene. Pero ahora interesa ver la acción Operar dirección grafo como se observa en la Figura. Vea que aparece las frase "Todas las operaciones son ejecutadas con la matriz de adyacencia", no actuando sobre el JSON, con lo que la entrada será una matriz de adyacencia y la salida también será otra matriz de adyacencia, a partir de la cual se construye el nuevo grafo sometido a la operación.

Siguiendo el mismo ejemplo del grafo del primer apartado, que podemos importar con esta matriz de adyacencia:
0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1 0 0
y que volvemos a reproducir en la Figura, observando que la mayor parte de las flecha van arriba, entendiendo dirigido arriba como explicamos en el primer apartado, pues si j>i tenemos que la mitad o más de las aristas son j🡒i.
Así tenemos que en el grafo de la Figura hay 6 aristas 1🡒0, 2🡒0, 2🡒1, 3🡒1, 4🡒1, 4🡒2 que van arriba según esa definición, mientras que 2 van abajo 0🡒4, 3🡒4, constituyéndose por lo tanto en un grafo dirigido arriba, pues la mayor parte van desde un nodo con índice mayor que el de destino.

Al aplicar dirigido abajo cambiamos todas las direcciones. Si antes la mayor parte de las aristas iban arriba, ahora van abajo y por lo tanto es un grafo dirigido abajo según nuestra definición.
0 1 1 0 0 0 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0
Esto equivale a transponer la matriz de adyacencia, como se observa que es la transpuesta de la anterior cambiando filas por columnas.

Con la dirección todo arriba todas las aristas van desde un nodo con índice mayor que el del destino, como se observa en la Figura.
0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 1 1 0
La matriz de adyacencia tiene valores sólo en la parte inferior de la diagonal.

Con la dirección todo abajo las aristas van desde un nodo con índice menor que el del destino.
0 1 1 0 1 0 0 1 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0
La matriz tiene valores solo en la parte superior de la diagonal. Estas dos opciones todo arriba y todo abajo producen grafos acíclicos.

En la aplicación disponemos de la opción posicionar, que tras obtener la matriz de adyacencia con la nueva dirección aplicada, se reposicionan los nodos en su ubicación que previamente tenían en caso de que esa opción estuviera activada, operación que se ejecuta con el JSON. Todos los ejemplos anteriores se han ejecutado con esta opción activada.
En la Figura vemos el resultado equivalente a todo abajo que vimos en la Figura, pero ahora con la opción posicionar desactivada, ubicándose lo nodos en la posición automática por niveles que se obtiene directamente desde la matriz de adyacencia.

Vea que la arista "1🡒4" queda oculta detrás, que podemos descubrir si cambiamos la posición del nodo "2", como se observa en la Figura. Este grafo es estructuralmente el mismo que el de la Figura.
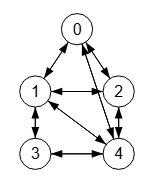
Con la dirección todo dirigido hay que recordar lo que dijimos en apartado anterior sobre cambiar la direccionalidad que actuaba sobre el JSON, donde sí podíamos convertir el grafo en todo dirigido actuando sobre el JSON, como el grafo de la Figura, pero no siendo representable sobre la matriz de adyacencia, pues un grafo todo dirigido debe tener necesariamente una matriz simétrica y ya hemos dicho que la aplicación reserva las matrices simétricas para identificar única y exclusivamente a los grafos no dirigidos. Pero vamos a ver un truco para conseguir representar en una matriz de adyacencia modificada un grafo todo dirigido.
Al estudiar el tema del máximo flujo, un algoritmo que se debía ejecutar solo sobre grafos dirigidos aunque funcionaba también sobre los no dirigidos, expuse que usando la operación operateSubdivisionGraph() que veremos en un tema posterior podríamos solucionarlo.
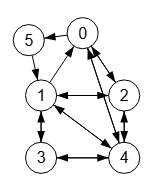
Como se observa en la Figura, aplicamos la operación subdivisión a la primera arista "0🡒1" que encontramos en el grafo, creándose el nuevo nodo "5" con sus aristas siguiendo la dirección "0🡒5🡒1".
0 0 1 0 1 1 1 0 1 1 1 0 1 1 0 0 1 0 0 1 0 0 1 0 1 1 1 1 0 0 0 1 0 0 0 0
Esto equivale a añadir una nueva columna y una nueva fila a la matriz de adyacencia, traslando el valor de la posición "0,1" al correspondiente en la columna o fila. Esto hace que la matriz deje de ser simétrica y representa entonces un grafo todo dirigido. Este tipo de transformación no afecta a algoritmos como el del máximo flujo.

Y por último con no dirigido eliminamos todas las direcciones.
0 1 1 0 1 1 0 1 1 1 1 1 0 0 1 0 1 0 0 1 1 1 1 1 0
La matriz de adyacencia es simétrica, representando única y exclusivamente un grafo no dirigido.
El botón con la leyenda "Código" que vemos en la Figura nos permite acceder al código JavaScript que ejecuta la operación operateDirectionGraph() exclusivamente sobre la matriz de adyacencia, devolviendo a su vez otra matriz de adyacencia:
function operateDirectionGraph({matrix=[], edgesDirection="none", removeEdgeValues=false}) {
let dev = {error: "", matrix: []}, temp;
try {
if (temp = getMatrixModeValue({matrix}), typeof temp==="string") throw new Error(temp);
let [modeValue, nullValue] = temp;
if (modeValue!=="0/1" && removeEdgeValues) {
matrix = matrix.map(v => v.map(w => w===nullValue ? 0 : 1));
modeValue = "0/1";
nullValue = 0;
}
let n = matrix.length;
if (edgesDirection==="undirected") {
dev.matrix = Array.from({length: n}, () => Array.from({length: n}, () => nullValue));
for (let i=0; i<n; i++){
for (let j=i; j<n; j++) {
let value = nullValue;
if (matrix[i][j]!==nullValue) {
value = matrix[i][j];
} else if (matrix[j][i]!==nullValue) {
value = matrix[j][i];
}
dev.matrix[i][j] = value;
dev.matrix[j][i] = value;
}
}
} else if (edgesDirection==="directed-all") {
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
dev.matrix = JSON.parse(JSON.stringify(matrix));
if (directed) {
let value = (modeValue==="0/number" || modeValue==="0/1") ? 1 :
modeValue==="false/true" ? true :
modeValue = "";
for (let i=0; i<n; i++){
for (let j=0; j<n; j++) {
if (i!==j) {
if (dev.matrix[i][j]!==nullValue && dev.matrix[j][i]===nullValue) {
dev.matrix[j][i] = value
} else if (dev.matrix[i][j]===nullValue && dev.matrix[j][i]!==nullValue) {
dev.matrix[i][j] = value;
}
}
}
}
}
let edges = getEdges({matrix:dev.matrix, edgesCompact:true});
if (typeof edges=="string") throw new Error(edges);
if (edges.length>0) {
let [ie, je] = edges[0];
let value = dev.matrix[ie][je];
dev.matrix[ie][je] = nullValue;
for (let i=0; i<n; i++) {
dev.matrix[i].push(i===ie ? value : nullValue);
}
let arr = Array.from({length: n+1}, (v,i) => i===je ? value : nullValue);
dev.matrix.push(arr);
}
} else if (edgesDirection!=="none") {
dev.matrix = Array.from({length: n}, () => Array.from({length: n}, () => nullValue));
for (let i=0; i<n; i++){
for (let j=0; j<n; j++) {
if (matrix[i][j]!==nullValue) {
if (edgesDirection==="directed-up"){
dev.matrix[i][j] = matrix[i][j];
dev.matrix[j][i] = nullValue;
} else if (edgesDirection==="directed-down"){
dev.matrix[i][j] = nullValue;
dev.matrix[j][i] = matrix[i][j];
} else if (edgesDirection==="all-up"){
if (i<j) {
dev.matrix[j][i] = matrix[i][j];
dev.matrix[i][j] = nullValue;
} else {
dev.matrix[j][i] = nullValue;
dev.matrix[i][j] = matrix[i][j];
}
} else if (edgesDirection==="all-down"){
if (i>j) {
dev.matrix[j][i] = matrix[i][j];
dev.matrix[i][j] = nullValue;
} else {
dev.matrix[j][i] = nullValue;
dev.matrix[i][j] = matrix[i][j];
}
}
}
}
}
}
} catch(e){dev.error = `#Error operateDirectionGraph(): ${clean(e.message)}`}
return dev;
}El argumento edgesDirection es la dirección que puede ser none, undirected, directed-up, directed-down, all-up, all-down para las opciones ninguno, no dirigido, dirigido arriba, dirigido abajo, todo arriba y todo abajo respectivamente.
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
El valor none, del que no pusimos ningún ejemplo antes, simplemente eliminará todas las aristas. La matriz de adyacencia tendrá todos los valores cero.
En el código aparece la función auxiliar Obtener modo valores de la matriz, que veremos más abajo en getMatrixModeValue() incluida en la sección de algoritmos, función que usamos para eliminar los valores de las aristas en caso de que se pase el argumento removeEdgeValues activado.
Exportando a Wolfram con operateDirectionGraph()

Para todas las operaciones se exporta el código para ejecutar en Wolfram Cloud. Empecemos por la operación no dirigido que convierte un grafo que inicialmente es dirigido arriba, que ya vimos en el apartado anterior y que exponemos nuevamente en la Figura compuesta con ambos grafos.
0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1 0 0
Esta es la matriz de adyacencia que generaba el grafo dirigido arriba.

En la Figura podemos ver el grafo original dirigido arriba que se nos presenta en Wolfram Cloud, donde la mayor parte de las aristas van de un nodo con índice mayor que el de destino igual que el nuestro, aunque la disposición espacial pueda ser diferente. Y el grafo no dirigido usando la función UndirectedGraph[g]. En la aplicación se ofrece ese enlace a información en Wolfram Documentacion Center y, cuando esté disponible, también en MathWorld Wolfram Undirected Graph.
El siguiente código para Wolfram Cloud separa cada sentencia con una línea horizontal, pues las sentencias en Wolfram se separan por salto de línea. La primera presenta el grafo inicial. La segunda aplica la operación UndirectedGraph[g] para obtener el grafo no dirigido.
g = AdjacencyGraph[{{0,1,1,0,1},{1,0,1,1,1},{1,1,0,0,1},{0,1,0,0,1},{1,1,1,1,0}}, ImageSize->250,
VertexSize->{"Scaled", 0.13}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center]},
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}]
UndirectedGraph[g]
Veamos ahora el ejemplo para operar dirigido abajo un grafo que inicialmente es dirigido arriba, que ya vimos en el apartado anterior y que exponemos nuevamente en la Figura compuesta con ambos grafos. Como el original era dirigido arriba, se trata de hacer una transposición de la matriz de adyacencia.
0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1 0 0
Esta es la matriz de adyacencia que generaba el grafo dirigido arriba.

En la Figura vemos el resultado obtenido en Wolfram, con una distinta disposición gráfica de los nodos, pero con la misma relación de aristas. En el código Wolfram que exponemos a continuación, donde separamos cada sentencia con una línea horizontal, pues las sentencias en Wolfram se separan por salto de línea.
Separamos la configuración c del grafo original para luego incluirla en el final y darle el mismo estilo que el original. Observe la definición de la función f = First[#]<Last[#]&; tal que si vamos a convertir dirigido abajo el condicional es el que aparece < y para dirigido arriba sería >. Aplicando Map con esa función a la lista de aristas l contamos cuántas aristas hay en uno u otro sentido con Count. Aplicando el condicional If devolvemos la matriz sin cambios o la transpuesta con Transpose en función de si es dirigido arriba u>=v o abajo u<v. Finalmente aplicamos AdjacencyGraph para construir el grafo final.
c = {ImageSize->250, VertexSize->{"Scaled", 0.13},
VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, DirectedEdges->True,
EdgeStyle->{{Black,Thickness[0.005]}}};
g = AdjacencyGraph[{{0,0,0,0,1},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}}, c]
x = AdjacencyMatrix[g];
z = Transpose[x];
l = EdgeList[g];
f = First[#]<Last[#]&;
a = Count[Map[f,l], True];
b = Count[Map[f,l], False];
ff[u_,v_] := If[u>=v, x, z];
y = ff[a, b];
AdjacencyGraph[y, c]No he conseguido aplicar de una forma directa esta operación en Wolfram, por lo que los enlaces que ofrece la aplicación no conducen a información concreta. Si lo desea puede ver cada una de las funciones auxiliares en Wolfram Documentation Center: AdjacencyMatrix, Transpose, EdgeList, First, Last, Count, If, AdjacencyGraph.
Hay una forma indirecta cuando lo que se trata es de convertir entre dirigido arriba y dirigido abajo, que es usando la función ReverseGraph[g] que cambia la dirección de todas las aristas, obteniéndose exactamente lo mismo que la Figura con este código:
c = {ImageSize->250, VertexSize->{"Scaled", 0.13},
VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, DirectedEdges->True,
EdgeStyle->{{Black,Thickness[0.005]}}};
g = AdjacencyGraph[{{0,0,0,0,1},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}}, c]
ReverseGraph[g]
Veamos ahora el ejemplo para operar todo abajo un grafo que inicialmente es dirigido arriba, que ya vimos en el apartado anterior y que exponemos nuevamente en la Figura compuesta con ambos grafos.
El inicial es un grafo donde donde la mayor parte de las aristas van de un nodo con índice mayor que el de destino. Mientras que el resultado de la operación todo abajo es un grafo donde todas las aristas van de un nodo con menor índice que el de destino.
0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1 0 0
Esta es la matriz de adyacencia que generaba el grafo dirigido arriba.

En la Figura vemos en Wolfram Cloud el grafo original dirigido arriba y el resultado todo abajo.
El código que se ofrece a continuación a ejecutar en Wolfram Cloud se basa en las funciones DirectedGraph y UndirectedGraph. Primero obtenemos el grafo no dirigido con UndirectedGraph[g] y aplicarle DirectedGraph[UndirectedGraph[g], "Acyclic"] con el argumento Acyclic, haciendo que el grafo sea acíclico, lo que forzará a que todas las aristas se implementen abajo, es decir, desde nodos con menor índice a destinos con mayor índice.
g = AdjacencyGraph[{{0,0,0,0,1},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}},
ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels->{1->Placed[0,Center],
2->Placed[1,Center], 3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center]},
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
DirectedGraph[UndirectedGraph[g], "Acyclic"]
Veamos ahora el ejemplo para operar todo arriba un grafo que inicialmente es dirigido arriba, que ya vimos en el apartado anterior y que exponemos nuevamente en la Figura compuesta con ambos grafos.
0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1 0 0
Esta es la matriz de adyacencia que generaba el grafo dirigido arriba.

El grafo dirigido arriba tiene todas las aristas con nodos de mayor índice que el de destino. Nuevamente hace el grafo acíclico. En la Figura vemos el resultado en Wolfram.
No he encontrado una forma directa de hacer esto en Wolfram, pues usando h = DirectedGraph[UndirectedGraph[g], "Acyclic"] tendremos un grafo dirigido abajo, como vimos antes. Pero podemos aplicar x = Transpose[AdjacencyMatrix[h]] para transponer su matriz y representarlo como grafo con AdjacencyGraph[x, c], para lo cual al inicio tuvimos que extraer la configuración de estilo del grafo inicial en la variable c.
c = {ImageSize->250, VertexSize->{"Scaled", 0.13},
VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center],
4->Placed[3,Center], 5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, DirectedEdges->True,
EdgeStyle->{{Black,Thickness[0.005]}}};
g = AdjacencyGraph[{{0,0,0,0,1},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}}, c]
h = DirectedGraph[UndirectedGraph[g], "Acyclic"];
x = Transpose[AdjacencyMatrix[h]];
AdjacencyGraph[x, c]Grafo todo dirigido (o con todas las aristas dobles) en Wolfram

Por último veamos como Wolfram puede forzar un grafo no dirigido a uno todo dirigido, que también podemos denominar con todas las aristas dobles.
0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1 0 0
Empezamos con el mismo grafo inicial dirigido arriba que hemos usado en los ejemplos anteriores y que se almacena en la variable g. El primer resultado de la Figura es un grafo no dirigido, que se consigue con h = UndirectedGraph[g].
Con MatrixForm[AdjacencyMatrix[h]] obtenemos la matriz de adyacencia del grafo no dirigido anterior, observando que es simétrica tal y como debe corresponder a un no dirigido.
Con j = DirectedGraph[h] forzamos a todo dirigido el grafo no dirigido anterior.
Con MatrixForm[AdjacencyMatrix[j]] obtenemos la matriz de adyacencia de este grafo dirigido, observando que es la misma matriz de adyacencia que el no dirigido. Por eso esta operación no se contempla en operateDirectionGraph(), pues como devuelve una matriz, esta debe ser única para cada representación del grafo.
g = AdjacencyGraph[{{0,0,0,0,1},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}}, ImageSize->250,
VertexSize->{"Scaled", 0.13}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, DirectedEdges->True,
EdgeStyle->{{Black,Thickness[0.005]}}]
h = UndirectedGraph[g]
MatrixForm[AdjacencyMatrix[h]]
j = DirectedGraph[h]
MatrixForm[AdjacencyMatrix[j]]

Recordemos que podemos conseguir un grafo todo dirigido con la utilidad para cambiar la direccionalidad del grafo, donde obtuvimos el grafo de la Figura, donde todas las aristas son dobles, apareciendo gráficamente sobrepuestas, pero que pueden separarse visualmente como ya vimos en ese apartado. La exportación directa a Wolfram se observa en la Figura.
Como observamos en el siguiente código, la matriz de adyacencia es la simétrica que daría lugar a un grafo no dirigido. Pero la directiva DirectedEdges->True fuerza el grafo a todo dirigido.
g = AdjacencyGraph[{{0,1,1,0,1},{1,0,1,1,1},{1,1,0,0,1},{0,1,0,0,1},{1,1,1,1,0}}, ImageSize->250,
VertexSize->{"Scaled", 0.13}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center],
3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center]},
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}]Obtener modo valores getMatrixModeValue()

Como se observa en la Figura, en la parte inferior del panel izquierdo encontramos la sección acciones donde podemos ejecutar algoritmos sobre el grafo. Tal como indica el comentario, todos los algoritmos se ejecutan con la matriz de adyacencia. No modifican la estructura del grafo, aunque pueden modificar el estilo cambiando la presentación. Los algoritmos devuelven diferentes resultados dependiendo de la acción que llevemos a cabo. En la parte inferior se expone también el codigo JavaScript que se ejecuta.
En este caso ejecutamos el algoritmo para obtener el modo valores de la matriz, ejecutándose getMatrixModeValue({matrix}), donde el argumento matrix es la matriz de adyacencia que la aplicación obtiene del grafo, como se explica en el tema estructuras de datos, en el apartado dedicado a la matriz de adyacencia.
El valor devuelto por el algoritmo es el Array ["null/value", null] para ese ejemplo, donde el primer valor es un String con el modo entre null/value, 0/number, 0/1 y false/true. El segundo es el valor que hace nula la arista, pudiendo ser los valores null, 0, false.
A continuación exponemos el código del algoritmo:
function getMatrixModeValue({matrix=[]}) {
let result = ["", undefined];
try {
let mflat = matrix.flat();
if (mflat.every(v => v===true || v===false)){
result = ["false/true", false];
} else if (mflat.every(v => v===0 || v===1) || mflat.every(v => v==="")){
result = ["0/1", 0];
} else if (mflat.every(v => typeof v==="number")) {
result = ["0/number", 0];
} else if (mflat.every(v => v===null || typeof v==="string" || typeof v==="number")){
result = ["null/value", null];
}
if (result[0]==="") throw new Error("Unknown");
} catch(e){result = e.message}
return result;
}Es el grafo dirigido isGraphDirected()
Otro de los algoritmos que podemos encontrar en la sección acciones y que tiene que ver con la direccionalidad del grafo es cuestionar si el grafo es dirigido (a los grafos dirigidos también se les denomina digrafos), usando el algoritmo isGraphDirected({matrix}).
function isGraphDirected({matrix=[]}){
let result = false;
try {
result = matrix.some((v,i) => v.some((w,j) => matrix[i][j]!==matrix[j][i]));
} catch(e){result = e.message}
return result;
}El algoritmo es muy simple y se basa en comprobar la simetría de la matriz. Si para todo i, j sucede que matrix[i][j] = matrix[j][i] entonces la matriz es simétrica y el grafo es no dirigido. En otro caso será dirigido.
Obtener dirección getDirection()
Dirigido arriba: 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1 0 0 Dirigido abajo 0 1 1 0 0 0 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0
Como explicamos más arriba sobre grafos dirigido arriba y abajo, podemos detectar en la matriz donde hay más valores no nulos en la matriz de adyacencia. En la primera matriz de la izquierda vemos que hay más "1" por debajo de la diagonal que por encima, constituyéndose en un grafo dirigido arriba según nuestro convenio. El otro es dirigido abajo pues tiene más "1" por encima de la diagonal.
El algoritmo getDirection({matrix}) comprueba primero si el grafo es dirigido usando el algoritmo isGraphDirected() que ya vimos en el apartado anterior. Si no es dirigido devuelve ["undirected"]. Si es dirigido cuenta los valores no nulos por encima y por debajo de la diagonal devolviendo ["directed-up"] o ["directed-down"] según el caso
function getDirection({matrix=[]}){
let result = [], temp;
try {
if (temp = isGraphDirected({matrix}), typeof temp==="string") throw new Error(temp);
if (!temp) {
result = ["undirected"];
} else {
if (temp = getMatrixModeValue({matrix}), typeof temp==="string") throw new Error (temp);
let [modeValue, nullValue] = temp;
let diagonalTop = 0;
let diagonalDown = 0;
let n = matrix.length;
for (let i=0; i<n; i++){
for (let j=i; j<n; j++){
if (matrix[i][j]!==nullValue) diagonalTop++;
if (matrix[j][i]!==nullValue) diagonalDown++;
}
}
if (diagonalDown>=diagonalTop) {
result = ["directed-up"];
} else {
result = ["directed-down"];
}
}
if (result.length===0) throw new Error("Unknown");
} catch(e){result = "Error: " + e.message}
return result;
}Para obtener el valor nulo de las aristas usamos el algoritmo getMatrixModeValue() que ya vimos en un apartado anterior.
Obtener matriz no dirigida getUndirectedMatrix()

En la Figura tenemos un grafo con valores numéricos en todas las aristas menos una "D🡒E" que tiene el valor "X". Podemos importar en la aplicación la siguiente matriz de adyacencia con modo valores null/value para generar ese grafo:
[[null, null, null, null, null], [10, null, null, null, null], [20, 30, null, null, null], [null, 40, null, null, "X"], [null, 50, 60, null, null]]
[[0, 0, 0, 0, 0], [10, 0, 0, 0, 0], [20, 30, 0, 0, 0], [0, 40, 0, 0, 1], [0, 50, 60, 0, 0]]
Si cambiamos el valor de la arista "D🡒E" con un valor numérico como 1, o incluso si eliminamos el valor de esa arista, la matriz de adyacencia se puede representar en el modo 0/number. Si importa esta matriz en la aplicación verá que obtiene el mismo grafo con la arista "D🡒E" con valor 1.
Time: 0 ms Matriz no dirigida: [[0,10,20,0,0], [10,0,30,40,50], [20,30,0,0,60], [0,40,0,0,1], [0,50,60,1,0]]
Los algoritmos usan matrices de adyacencia exclusivamente en los modos 0/number y 0/1. Así que antes de ejecutarse el algoritmo, la aplicación convertirá los otros modos null/value o false/true en los otros modos admitidos.
Con el algoritmo de este apartado getUndirectedMatrix({matrix}) se recibe la matriz de un grafo dirigido o no dirigido en alguno de esos modos y devuelve una matriz no dirigida en el mismo modo.
function getUndirectedMatrix({matrix=[]}){
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
if (directed) {
let n = matrix.length;
for (let i=0; i<n; i++) {
for (let j=0; j<n; j++) {
if (i!==j) {
if (matrix[i][j]!==0 && matrix[j][i]===0) {
matrix[j][i] = matrix[i][j];
} else if (matrix[j][i]!==0 && matrix[i][j]===0) {
matrix[i][j] = matrix[j][i];
}
}
}
}
}
return matrix;
}El algoritmo usa isGraphDirected() que ya vimos en un apartado anterior.
Obtener matriz dirigida getDirectedMatrix()
Time: 1 ms Matriz dirigida: [[0,0,0,0,0], [10,0,0,0,0], [20,30,0,0,0], [0,40,0,0,0], [0,50,60,1,0]]
Este algoritmo recibe una matriz de adyacencia y devuelve la matriz dirigida, con las mismas consideraciones que vimos en el apartado anterior. El resultado de los algoritmos siempre devuelve un único valor, en este caso una matriz, no devolviendo nunca un String pues nos servirá para detectar que se ha generado un error, siendo ese valor String el mensaje de error. Si es necesario devolver un String lo encerramos en un Array por ejemplo. La aplicación presenta además el tiempo de ejecución, que en este caso es insignificante, y comentarios y aclaraciones junto al resultado.
function getDirectedMatrix({matrix=[]}){
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
if (!directed) {
let n = matrix.length;
for (let i=0; i<n; i++) {
for (let j=i+1; j<n; j++) {
matrix[i][j] = 0;
}
}
}
return matrix;
}Operar grafo transpuesto operateTransposeGraph()

Aún hay otra operaración que podemos ejecutar sobre la direccionalidad del grafo y es operar grafo transpuesto, como se observa en la Figura. Las operaciones se presentan con el botón .
"error":"", "matrix": [[0,1,1,1], [0,0,1,0], [0,0,1,1], [0,0,0,0]]}
La operación devuelve un objeto con el posible mensaje de error y la matriz de adyacencia transpuesta del grafo original, modificando el grafo en la aplicación. Con el botón "Codigo" que vemos en la Figura tenemos acceso al código de la operación que se ejecuta:
function operateTransposeGraph({matrix=[]}){
let dev = {error: "", matrix: []}, temp;
try {
temp = getMatrixModeValue({matrix});
if (typeof temp==="string") throw new Error(temp)
let [modeValue, nullValue] = temp;
let n = matrix.length;
dev.matrix = Array.from({length: n}, () => Array.from({length: n}, () => nullValue));
for (let i=0; i<n; i++) {
for (let j=0; j<n; j++){
dev.matrix[i][j] = matrix[j][i];
}
}
} catch(e){dev.error = `#Error operateTransposeGraph(): ${clean(e.message)}`}
return dev;
}Vea que usamos el algoritmo getMatrixModeValue() que ya vimos en un apartado anterior, usándose para obtener el valor nulo nullValue y construir la matriz de adyacencia vacía.