Algoritmos CRC con tabla
Algoritmo para obtener el CRC usando una tabla
En los temas anteriores hemos aplicado mejoras empezando por el algoritmo de la división para obtener el resto, pasando al algoritmo del resto pues no nos interesaba el cociente de la división, mejorándolo con otro para evitar el aumento de la entrada y por último llegábamos al algoritmo con índice de un byte, donde pasábamos al tercer argumento de la función mod(x, y, z) un índice que era un valor binario entre 256 posibles. Esta mejora que veremos en este tema nos permitirá almacenar en una tabla esos 256 valores para no tener que estar calculándolos con cada byte del archivo.
Habíamos terminado el tema anterior con la recurrencia siguiente, donde x[i, d] es el byte tomado en la iteración i-ésima, con una longitud de d bits. Y que ρ es el resto r'i-1 de la iteración anterior. Con r' indicamos que es el CRC de la entrada aumentada, aunque se obtiene sobre la entrada sin aumentar x, no sobre x':
r'i = mod( 0d , y , ( x[i, d] + ρ[0, d] ) 10w-d ) + ρ[d, w-d] 10d
Como x[i, d] + ρ[0, d] ocupa 8 bits, este término sólo tendrá 28 = 256 valores posibles. Así que tendremos 256 índices entre 0·10w-d y 11111111·10w-d, lo que nos permitirá almacenarlos en un tabla y no tener que estar ejecutando mod(0, poly, index) con cada byte del bucle, algo que haremos en este apartado.
Vease que no es necesario multiplicar x[i, d] + ρ[0, d] por 10w-d para componer el índice de la tabla, puesto que este agregado de w-d ceros lo tendremos en cuenta cuando generemos la tabla con los 256 resultados posibles de la expresión (x[i, d] + ρ[0, d]) 10w-d.
Así que nuestra recurrencia queda como sigue:
r'i = table[x[i, d] + ρ[0, d]] + ρ[d, w-d] 10d
Veamos como generamos la tabla.Supongamos que index = 01111010, 0x7A en hexadecimal, 122 en decimal, letra "z" en ASCII. Y que el polinomio es 0x9B con un ancho w = 8 bits (CRC-8/LTE). Agregando el 1 inicial es poly = (1)10011011. En la herramienta Web Tools online podemos obtener mod(08, poly, index) = mod(08, 110011011, 01111010) = 00101010 con la siguiente traza:
00000000 MOD 110011011 ⇒
001111010 00000000
k=0 011110100 0000000
k=1 111101000 000000
111101000 XOR 110011011 = 001110011
k=2 011100110 00000
k=3 111001100 0000
111001100 XOR 110011011 = 001010111
k=4 010101110 000
k=5 101011100 00
101011100 XOR 110011011 = 011000111
k=6 110001110 0
110001110 XOR 110011011 = 000010101
k=7 000101010 Podemos observar que el primer 1 del polinomio no afecta al resultado final, pues el primer dígito del resto siempre será cero, resaltado en azul. El resto tiene w= 8 dígitos y se resalta en amarillo. Así que podríamos ahorrarnos este primer 1 en poly = (1)10011011 y el polinomio pasaría a ser poly = 10011011 si hiciéramos una ligera modificación en el cálculo anterior de la siguiente forma:
Poly 10011011 Trace for index=0b01111010, 0x7A, 122 : j=0 ⇒ 01111010 << 1 = 11110100 = 11110100 ⇒ 0xF4 j=1 ⇒ 11110100 << 1 = 11101000 ^ Poly = 01110011 ⇒ 0x73 j=2 ⇒ 01110011 << 1 = 11100110 = 11100110 ⇒ 0xE6 j=3 ⇒ 11100110 << 1 = 11001100 ^ Poly = 01010111 ⇒ 0x57 j=4 ⇒ 01010111 << 1 = 10101110 = 10101110 ⇒ 0xAE j=5 ⇒ 10101110 << 1 = 01011100 ^ Poly = 11000111 ⇒ 0xC7 j=6 ⇒ 11000111 << 1 = 10001110 ^ Poly = 00010101 ⇒ 0x15 j=7 ⇒ 00010101 << 1 = 00101010 = 00101010 ⇒ 0x2A
Como el dividendo, es decir 08 en mod(08, 110011011, 01111010), son siempre 8 ceros, sólo es necesario tener en cuenta el tercer argumento, es decir, el índice 01111010. Iteramos de 0 a 7 desplazando un bit a la izquierda, lo que equivale a eliminar el primer bit por la izquierda y agregar un cero por la derecha. Si el primer bit es un uno entonces sumamos XOR (^) con el poly (sin el (1) inicial) .
Se trata entonces de iterar por los 256 valores posibles del índice, entre 0b00000000 y 0b11111111, 0 y 255 en decimal, e ir obteniendo el resto de cada índice. Cada uno de estos índices se multiplica por 10w-d. En el ejemplo como w = 8 y d = 8 entonces 10w-d = 1 y no produce ningún efecto. Si fuera un polinomio con ancho w = 24 bits multiplicaríamos por 1016 lo que equivale a agregar 16 ceros al índice antes de iniciar el bucle de generación. Ambos procedimientos son totalmente equivalentes, hacen lo mismo.
El código para generar la tabla es el siguiente:
let widthBits = Math.max(width, 8);
poly = hexToBin(poly).padStart(width, "0").padEnd(widthBits, "0");
let table = [];
for (let i=0; i<256; i++){
let n = i.toString(2).padStart(8, "0") + "0".repeat(widthBits-8);
for (let j=0; j<8; j++){
let shifted = shiftLeft(n, 1);
if (n[0] === "1") {
n = xor(shifted, poly).padStart(widthBits, "0");
} else {
n = shifted;
}
}
table.push(n);
}Observe que no agregamos el (1) inicial al polinomio. Como en ejemplos anteriores, primero ajustamos al inicio al ancho w del polinomio (width en el código) y luego realizamos el ajuste al final para el caso de los polinomios con ancho inferior a 8. Esto ya fue explicado en el tema anterior.
Iteramos entre 0 y 255, pasando cada uno de estos números a binario con let n = i.toString(2). Ajustamos ceros a la izquierda para que tenga 8 bits. Y luego concatenamos por la derecha con "0".repeat(widthBits-8) para ejecutar la multiplicación del índice por 10w-d. Si w = d = 8 no tiene ningún efecto. Si fuera mayor, como w = 24, entonces multiplicamos por 1024-8 = 1016, lo que equivale a agregar widthBits-8 ceros a la derecha.
Desplazamos a la izquierda un bit y comprobamos si el primer bit es un uno, en cuyo caso sumamos XOR con el polinomio (sin el (1) inicial). Completamos con ceros por la izquierda pues la operación XOR elimina los ceros iniciales. Guardamos el resultado en la posición index de la tabla con table.push(n).
Repetimos nuevamente la recurrencia junto al esquema para comentar más detalles:
r'i = table[x[i, d] + ρ[0, d]] + ρ[d, w-d] 10d
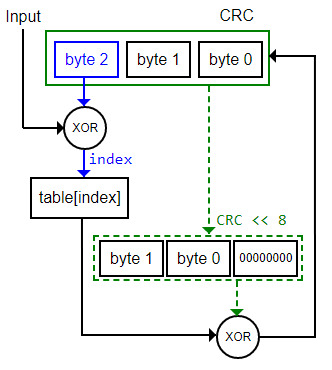
En el esquema de la Figura se presenta un CRC de 24 bits, 3 bytes. En input está la entrada sin aumentar de los bytes del archivo. El registro CRC se modifica en cada iteración de los bytes del archivo, resultando el CRC final cuando finalice el bucle.
Podemos identificar el top byte del CRC del paso anterior (byte 2) con ρ[0, d]. El byte de la entrada (input) es x[i, d]. La suma XOR entre ambos produce un índice (index) entre 0 y 255. Ese índice nos dará un valor en table[index].
Desplazamos el CRC del paso anterior 8 bits a la izquierda, que es el resultado de calcular ρ[d, w-d] 10d. Sumamos XOR con el valor de la tabla. El resultado será el nuevo CRC para el paso siguiente del bucle.
El código siguiente expone la función crcTableStringBasic() que implementa lo que hemos visto. No olvide que seguimos usando binarios representados en strings. En un siguiente apartado convertiremos este algoritmo en uno final con números binarios.
function crcTableStringBasic({arrayBytes=[], width=0, poly="0"}){
let widthBits = Math.max(width, 8);
poly = hexToBin(poly).padStart(width, "0").padEnd(widthBits, "0");
let table = [];
for (let i=0; i<256; i++){
let n = i.toString(2).padStart(8, "0") + "0".repeat(widthBits-8);
for (let j=0; j<8; j++){
let shifted = shiftLeft(n, 1);
if (n[0] === "1") {
n = xor(shifted, poly).padStart(widthBits, "0");
} else {
n = shifted;
}
}
table.push(n);
}
let crc = "0".repeat(widthBits);
for (let i=0; i<arrayBytes.length; i++){
let Byte = arrayBytes[i].toString(2).padStart(8, "0");
let crcTopByte = shiftRight(crc, widthBits-8);
let index = xor(crcTopByte, Byte);
let tab = table[Number(`0b${index}`)];
let crcShift = shiftLeft(crc, 8);
crc = xor(crcShift, tab).padStart(widthBits, "0");
}
crc = crc.substr(0, width);
return crc;
}En el código anterior widthBits es el ancho w en bits del polinomio, sin incluir el (1) inicial. Ajustamos a 8 bits para el caso de polinomios con ancho inferior. Como el argumento poly es un hexadecimal representado en un string, usamos la función hexToBin(poly) que expusimos en un tema anterior para convertir a binario en string. No incluimos el (1) inicial. Rellenamos ceros por la izquierda para completar el tamaño w y, si el polinomio es tal que w<8, agregamos 8-w ceros por la derecha, lo que equivale a rellenar con padEnd(widthBits, "0"). Vease que si w≥8 entonces width es igual que widthBits y no produce ningún efecto el relleno por la derecha.
El siguiente paso es generar la tabla en un bucle que itera entre i=0 y i=255. En cada iteración convertimos i en un binario en string, completando con ceros a la izquierda 8 bits. Y agregando w-8 (widthBits-8) ceros a la derecha. Con esto multiplicamos por 10w-d el índice, pues en la recurrencia teníamos table[index] = (x[i, d] + ρ[0, d]) 10w-d.
Iteramos por los bits del índice n desde j=0 hasta j=7. Desplazamos un bit a la izquierda con shiftLeft(n, 1). Cuando el primer bit de la izquierda sea 1 sumaremos XOR con el polinomio. Al final de este bucle guardaremos el valor en la tabla.
A continuación se ejecuta el bucle que itera por los bytes de la entrada arrayBytes. Estos bytes nos vienen como números y los convertimos a binarios en string. Veamos una traza del CRC-24/LTE-A, polinomio de ancho w=24 bits, usando la entrada "123456789", presentando sólo la iteración del tercer byte (i=2):
i=2 ⇒ byte = arrayBytes[2] = 00110011
crcTopByte = crc >>> 16 = 101101111000110010010001 >>> 16 = 000000000000000010110111
index = byte ^ crcTopByte = 00110011 ^ 000000000000000010110111 = 10000100 (132)
tab = table[index] = 101000001010000101000101 ⇒ 0xA0A145
crcShift = crc << 8 = 101101111000110010010001 << 8 = 100011001001000100000000
crc = crcShift ^ table[index] = 100011001001000100000000 ^ 1011000011000001000101 =
1011000011000001000101 ⇒ 0x2C3045En esta traza los desplazamientos derecha e izquierda se ejecutan con las funciones shiftRight() y shiftLeft() sobre binarios en strings, aunque en la traza aparezcan escritas con >>> y << respectivamente.
Obtenemos el crcTopByte desplazando a la derecha w-8 (widthBits-8) bits, que para este ejemplo es 32-8=16 bits. Observe en la traza que se obtienen los 8 primeros bits resaltados en amarillo. Calculamos el índice sumando XOR este crcTopByte con el byte de la entrada. Vamos a la tabla a recuperar el valor almacenado en este índice con table[Number(`0b${index}`)], no olvidando que index es un binario en string y que lo tenemos que convertir a número para obtener la posición en ese array. Con esto tenemos ya en la variable tab el término table[x[i, d] + ρ[0, d]] de nuestra recurrencia. Para obtener ρ[d, w-d] 10d desplazamos a la izquierda d=8, pues es como multiplicar por 10d. Finalizamos sumando XOR ambos términos.
Detalles de implementación con números binarios en JavaScript
Antes de pasar a implementar con números el algoritmo anterior, conviene repasar como JavaScript maneja las operaciones binarias a nivel de bit (bitwise operators). Estas son AND (&), OR (|), XOR (^), NOT (~) y los operadores de desplazamiento izquierda (<<) y derecha (>> y >>>). No deben confundirse los operadores binarios & y | con los operadores lógicos && o ||.
El máximo entero que podemos representar en JavaScript es 0x1FFFFFFFFFFFFF con valor decimal 9007199254740991, que tiene 53 bits 1. Sin embargo para las operaciones binarias a nivel de bit JavaScript usa un registro con solo 32 bits, conformando enteros positivos y negativos entre los máximos valores decimales -2147483648 y +2147483647.
Si ejecutamos una operación como 187 & 220 donde los operandos son números decimales, JavaScript convierte esos operandos en enteros de 32 bits y luego realiza la operación alineando los bits por la derecha y aplicando la operación AND (&) bit a bit:
187 = 00000000000000000000000010111011 220 = 00000000000000000000000011011100 187 & 220 = 152 = 00000000000000000000000010011000
La operación anterior puede ejecutarse con 0b10111011 & 0b11011100 usando binarios o también con 0xBB & 0xDC con hexadecimales.
Los bits a la izquierda que superen los 32 bits se descartan. Por ejemplo, si ejecutamos 12884902075 & 220 donde el valor del primer operando tiene a la izquierda dos bits uno que superan los 32 bits, tal como aparece resaltado en amarillo a continuación, vemos que son descartados, siendo de hecho el valor 187 para el primer operando como antes y generando el mismo resultado de la operación:
12884902075 = 1100000000000000000000000010111011 220 = 00000000000000000000000011011100 187 & 220 = 152 = 00000000000000000000000010011000
El primer bit a la izquierda o bit más significativo es el llamado bit de signo. Veamos los límites de estos números enteros, donde se observa que todos los números negativos tiene el primer bit a uno:
-2147483648 0b10000000000000000000000000000000 0x80000000 -255 0b11111111111111111111111100000001 0xFFFFFF01 -1 0b11111111111111111111111111111111 0xFFFFFFFF 0 0b00000000000000000000000000000000 0x00000000 +1 0b00000000000000000000000000000001 0x00000001 +255 0b00000000000000000000000011111111 0x000000FF +2147483647 0b01111111111111111111111111111111 0x7FFFFFFF
Los números negativos se manejan en complemento a dos. Por ejemplo, si JavaScript está operando -255 en operaciones a nivel de bit, toma el positivo 255, lo invierte con el operador NOT (~) y le suma 1:
255 = 0b00000000000000000000000011111111 0x000000FF
~255 = 0b11111111111111111111111100000000 0xFFFFFF00
1 = 0b00000000000000000000000000000001 0x00000001
~255+1 = -255 = 0b11111111111111111111111100000001 0xFFFFFF01El complemento a dos garantiza que el primer bit será siempre uno cuando el número es negativo y cero en otro caso. Si aplicamos el complemento a dos a un negativo obtenemos el positivo:
-255 = 0b11111111111111111111111100000001 0xFFFFFF01
~-255 = 0b00000000000000000000000011111110 0xFFFFFFFE
1 = 0b00000000000000000000000000000001 0x00000001
~-255+1 = 255 = 0b00000000000000000000000011111111 0x000000FFVease que aplicar NOT a un número negativo es como sumarle 0xFFFFFFFF, suma que producirá 1 bit de acarreo a la izquierda que supera 32 bits que será ignorado en operaciones a nivel de bit:
~-255 = ~11111111111111111111111100000001 = 00000000000000000000000011111110 -255+0xFFFFFFFF = 00000000000000000000000011111111 11111111111111111111111111111111 ───────────────────────────────── 100000000000000000000000011111110
En la implementación que haremos después manejaremos polinomios de 32 bits que pueden originar valores CRC negativos. Supongamos que obtenemos un valor CRC -255. Si hiciéramos (-255).toString(2) obtendríamos -0b11111111, -0xFF en hexadecimal. No podemos devolver este valor pues no es el verdadero binario que se esconde detrás del complemento a dos. Podemos deshacerlo con lo siguiente:
((-255)+0xFFFFFFFF+1).toString(2) = (4294967041).toString(2) = "11111111111111111111111100000001"
Como 0xFFFFFFFF + 1 = 0x100000000 = 232 también podemos hacerlo así:
((-255)+Math.pow(2, 32)).toString(2) = (4294967041).toString(2) = "11111111111111111111111100000001"
Veamos un ejemplo usando el polinomio 0x814141AB (CRC-32/AIXM) de ancho 32 bits, generando en la tabla el índice decimal 122 (0x7A), exponiendo los números en hexadecimal para que no ocupen mucho espacio en pantalla. Observe que aparecen algunos resultados negativos:
j=0 ⇒ 0x7A000000 << 1 = -0xC000000 = -0xC000000 j=1 ⇒ -0xC000000 << 1 = -0x18000000 ^ Poly = 0x694141AB j=2 ⇒ 0x694141AB << 1 = -0x2D7D7CAA = -0x2D7D7CAA j=3 ⇒ -0x2D7D7CAA << 1 = -0x5AFAF954 ^ Poly = 0x24444707 j=4 ⇒ 0x24444707 << 1 = 0x48888E0E = 0x48888E0E j=5 ⇒ 0x48888E0E << 1 = -0x6EEEE3E4 = -0x6EEEE3E4 j=6 ⇒ -0x6EEEE3E4 << 1 = 0x22223838 ^ Poly = -0x5C9C866D j=7 ⇒ -0x5C9C866D << 1 = 0x46C6F326 ^ Poly = -0x38784D73
En la traza convertimos cada valor numérico en un string, en este caso usando toString(16). Se observa por ejemplo que el primer valor 0x7A000000 es el que se inicia con el índice 0x7A multiplicado por 224 (agregando 24 ceros). En binario es un número que empieza con 01111010 y le siguen tres bytes ceros. Como el primer bit es un cero se trata de un número no negativo. Al desplazar un bit a la izquierda, el primer byte será 11110100, con lo que el registro de 32 bits tiene un primer bit puesto a uno y por tanto es un número negativo. Cualquier representación de ese número, como usando toString(), se realizará aplicando el complemento a dos:
n = 11110100 00000000 00000000 00000000 ⇒ F4000000 ~n = 00001011 11111111 11111111 11111111 ⇒ 0BFFFFFF 1 = 00000000 00000000 00000000 00000001 ⇒ 00000001 ~n+1 = 00001100 00000000 00000000 00000000 ⇒ -0C000000
Por lo tanto el binario real resultado de la operación 0x7A000000 << 1 es 0xF4000000 y no la representación en complemento a dos -0xC000000. Mientras ejecutamos el algoritmo no es necesarios hacer nada, puesto que JavaScript usará el binario real con las operaciones a nivel de bit. Pero si hacemos una traza usando toString(2), o bien cuando devolvamos el CRC al final del algoritmo, hemos de deshacer el complemento a dos si el numero es negativo. En la traza anteponemos el signo "#" para indicar su valor binario real:
j=0 ⇒ 0x7A000000 << 1 = #0xF4000000 = #0xF4000000
j=1 ⇒ #0xF4000000 << 1 = #0xE8000000 ^ Poly = 0x694141AB
j=2 ⇒ 0x694141AB << 1 = #0xD2828356 = #0xD2828356
j=3 ⇒ #0xD2828356 << 1 = #0xA50506AC ^ Poly = 0x24444707
j=4 ⇒ 0x24444707 << 1 = 0x48888E0E = 0x48888E0E
j=5 ⇒ 0x48888E0E << 1 = #0x91111C1C = #0x91111C1C
j=6 ⇒ #0x91111C1C << 1 = 0x22223838 ^ Poly = #0xA3637993
j=7 ⇒ #0xA3637993 << 1 = 0x46C6F326 ^ Poly = #0xC787B28D
El negativo aparece como resultado de una operación a nivel de bit:
0x7A000000 = 2046820352 0x80000000 = 2147483648 0x7A000000 << 1 = -0x0C000000 = -201326592 0x7A000000 | 0x80000000 = -0x06000000 = -100663296 0x7A000000 ^ 0x80000000 = -0x06000000 = -100663296 0x7A000000 + 0x80000000 = 0xFA000000 = 4194304000
Vease que la operaciones desplazamiento, OR y XOR generan un uno en el primer bit, generando un negativo. Mientras que la operación suma aritmética no funciona a nivel de bit y considera los números en formato de coma flotante (ver IEEE754). Observe a continuación como forzamos un negativo descubriendo el complemento a dos con la operación OR con un cero, mientras que la suma aritmética con un cero no modifica el valor:
(0xF4000000 + 0).toString(16) = 0xF4000000 (0xF4000000 | 0).toString(16) = -0x0C000000
En el apartado siguiente usaremos esto para saber cuando el primer bit es un uno.
Operadores de desplazamiento a nivel de bit en JavaScript
La operación desplazamiento a la derecha en JavaScript se ejecuta con el operador >>>. En los algoritmos basados en binarios en string hemos usado la función shiftRight(x, shift), donde x es un binario en string y shift es un número decimal con la cantidad de bits a desplazar:
function shiftRight(x="0", shift=0){
return "0".repeat(shift) + x.substr(0, x.length-shift);
}Usando el polinomio 0x814141AB con la entrada "123456789", en el byte i=3 con el algoritmo del apartado con binarios en string se realiza un desplazamiento de 24 bits a la derecha para obtener el crcTopByte usando esta función shiftRight():
crcTopByte =
shiftRight(crc, 24) =
shiftRight("11101000000000010111001001011000", 24) =
"11101000"Se observa que con esa operación obtenemos el primer byte de la izquierda. En la implementación del algoritmo que haremos en el siguiente apartado usando números, ejecutamos >>>, obvservando que el número es negativo pero se usa el número real sin complemento a dos, obteniéndose el mismo resultado:
crcTopByte = crc >>> 24 = #11101000000000010111001001011000 >>> 24 = 11101000
En JavaScript también existe el desplazamiento a la derecha conservando el signo >>, pero no es de aplicación puesto que estamos ignorando negativos. En cualquier caso el desplazamiento a la derecha se comporta igual en ambos casos.
El problema se plantea con el desplazamiento a la izquierda en JavaScript. Con binarios en string usamos la siguiente función:
function shiftLeft(x="0", shift=0) {
return x.substr(shift) + "0".repeat(shift);
}Esa función actúa sobre un registro cuya longitud viene dada por el argumento x. Si fuera necesario hay que pasar ceros a la izquierda para completar la longitud del registro. Mientras que en JavaScript tenemos el operador << que actúa siempre sobre un registro de 32 bits. Y esto supone una diferencia importante a tener en cuenta.
Por ejemplo, desplazar a la izquierda 3 bits sobre el binario en string "0011101111", que queremos que sea un registro de 10 bits para lo cual agreamos dos ceros a la izquierda:
shiftLeft("0011101111", 3) = "1101111000"Con esa función el ancho del registro viene determinado por la longitud del primer argumento, por lo que los tres primeros bits desaparecen por la izquierda y se agregan tres ceros por la derecha. Al final el resultado seguirá teniendo una longitud de 10 bits. Mientras que en JavaScript el ancho siempre es de 32 bits:
0b00000000000000000000000011101111 << 3 = 0b00000000000000000000011101111000
Obviamente no es mismo resultado. Para eliminar los bits a la izquierda mayor del ancho w=10 que estamos considerando, podemos hacer lo siguiente:
(0b11101111 << 3) & (Math.pow(2, 10)-1) = 1101111000
Se trata de aplicar un máscara con w=10 unos, resultado de 2w-1 = 210-1 = 10000000000 - 1 = 1111111111, con lo que eliminamos los bits sobrantes de la izquierda:
n = 00000000000000000000011101111000 210-1 = 00000000000000000000001111111111 n & (210-1) = 00000000000000000000001101111000
La otra complicación con el desplazamiento a la izquierda es que el número pudiera resultar negativo si el primer bit es un uno. Ya vimos antes que sólo debemos tenerlo en cuenta si vamos a dar salida a ese número con toString().
Por otro lado en el algoritmo con binarios en strings que hemos visto, cuando generabamos la tabla teníamos que comprobar que el primer bit era un uno. Como usábamos binarios en string era suficiente consultando n[0]==="1", dado que n era un string. En la implementación con números no podemos hacer eso pues manejaremos números. Podemos usar lo que vimos al final del apartado anterior: cuando el número es negativo entonces el primer bit es un uno. Bastaría consultar si (n|0) < 0, siempre y cuando n fuera un registro de w=32 bits, es decir, con polinomio de w=32 bits de ancho. Pero nuestros algoritmos deben prepararse para admitir polinomios de anchos inferiores a 32 bits. Así que usaremos ((n*Math.pow(2, 32-widthBits))|0) < 0. Se trata de agregar 32-w ceros a n, que tiene una longitud w, con lo que obtenemos un número binario de 32 bits y así podemos consultar si es negativo. Veamos un ejemplo.
w = 12 bits n = 110101101101 n·232-12 = n·220 = 11010110110100000000000000000000 (11010110110100000000000000000000 | 0) < 0 ⇒ true
El número 110101101101 tiene el primer bit a uno en un registro de w=12 bits. Al multiplicar agregamos 20 ceros, más los 12 del número hacen un total de 32 bits, lo que produce un negativo al operar OR con cero.
Hay otra forma para consultar si el primer bits es uno: n >>> (widthBits-1) & 1. Si n = 110101101101 es el mismo número del ejemplo anterior con un ancho w=12 bits, al desplazar 12-1 = 11 bits a la derecha su primer bit quedará ubicado en el bit menos significativo del registro de 32 bits de JavaScript. Consultando con un AND 1 sabremos si es o no un uno.
Implementación JavaScript del algoritmo CRC con números binarios
Con los visto en los apartados anteriores vamos a acometer la implementación en números binarios de JavaScript. Presentamos directamente el algoritmo siguiente, que no deja de ser el mismo que el visto en el primer apartado usando strings, pero ahora ajustándolo a números:
function crcTableBasic({arrayBytes=[], width=0, poly="0"}){
let widthBits = Math.max(width, 8);
poly = Number(`0x${poly}`) * Math.pow(2, widthBits-width);
let table = [];
for (let i=0; i<256; i++){
let n = i * Math.pow(2, widthBits-8);
for (let j=0; j<8; j++){
let shifted = (n<<1) & (Math.pow(2, widthBits)-1);
//también if (((n*Math.pow(2, 32-widthBits))|0) < 0)
if (n>>>(widthBits-1) & 1) {
n = shifted ^ poly;
} else {
n = shifted;
}
}
table.push(n);
}
let crc = 0;
for (let i=0; i<arrayBytes.length; i++){
let Byte = arrayBytes[i];
let crcTopByte = crc >>> (widthBits-8);
let index = crcTopByte ^ Byte;
let tab = table[index];
let crcShift = (crc<<8) & (Math.pow(2, widthBits)-1);
crc = crcShift ^ tab;
}
if (crc<0) crc += Math.pow(2, 32);
crc = crc / Math.pow(2, widthBits-width);
return crc;
}El argumento poly nos trae el polinomio en un string con valor hexadecimal. Lo convertimos a número con Number(`0x${poly}`) y lo multiplicamos por Math.pow(2, widthBits-width) para ajustarlo a polinomios con anchos inferiores a 8. Como widthBits = Math.max(width, 8) entonces lo anterior agrega ceros cuando el ancho del polinomio es inferior a 8 bits. Todo esto hace lo mismo que lo visto con strings hexToBin(poly).padStart(width, "0").padEnd(widthBits, "0").
A continuación entramos en el bucle que genera la tabla. El número n se multiplica por Math.pow(2, widthBits-8), pues debe tener el tamaño del polinomio. Dentro del bucle interno hay un desplazamiento a la izquierda, que ajustamos al ancho del polinomio con (n<<1) & (Math.pow(2, widthBits)-1), tal como vimos en el apartado anterior sobre la eliminación de los bits que sobresalen del registro de ancho widthBits por la izquierda. La consulta sobre si el primer bit es un uno la hacemos con n>>>(widthBits-1) & 1, ya explicado al final del apartado anterior. Incluimos un comentario con la otra forma de hacerlo. Dentro del bucle que itera por los bytes sólo hay que comentar el ajuste del desplazamiento a la izquierda, pues en el resto no hay que ajustar nada.
Al salir del bucle tenemos ya el CRC, que si fuera negativo deshacemos el complemento a dos como ya vimos en apartados anteriores. Finalizamos deshaciendo el ajuste inicial para polinomios inferiores a 8 bits, pues si al inicio multiplicamos el polinomio por Math.pow(2, widthBits-width), ahora dividimos el CRC por la misma cantidad. En esencia al inicio habíamos agregado widthBits-width ceros y ahora los quitamos.
Veamos una traza del CRC-24/LTE-A, polinomio de ancho w=24 bits, usando la entrada "123456789", presentando sólo la iteración del tercer byte (i=2) igual que lo expuesto al final del primer apartado:
i=2 ⇒ byte = arrayBytes[2] = 00110011
crcTopByte = crc >>> 16 = 101101111000110010010001 >>> 16 = 10110111
index = byte ^ crcTopByte = 00110011 ^ 10110111 = 10000100 (132)
tab = table[index] = 101000001010000101000101 ⇒ 0xA0A145
crcShift = crc << 8 = 101101111000110010010001 << 8 = 100011001001000100000000
crc = crcShift ^ table[index] = 100011001001000100000000 ^ 101101111000110010010001 =
001011000011000001000101 ⇒ 0x2C3045Se obtiene el mismo CRC parcial 0x2C3045 que con el algoritmo con binarios en string. Y al trabajar con números es más eficiente que el anterior que trabaja con strings. Pero tiene una limitación, pues con numeros binarios sólo podemos llegar hasta CRC de 32 bits, mientras que con strings no tenemos limitación de longitud. De todas formas en el tema siguiente veremos un algoritmo para generar CRC de cualquier longitud con números en JavaScript.
Invirtiendo los bits de un binario en JavaScript
El algoritmo anterior trabaja con números binarios en JavaScript y es más eficiente que el que trabaja con binarios en string del primer apartado. Podríamos afinar aún más evitando los ajustes que nos imponen los desplazamientos a la izquierda o la consulta del primer bit. Para ello antes vamos a ver como podemos invertir un número binario. Si tenemos el binario 00110101 y lo invertimos resultará 10101100. Esto parece fácil hacerlo manualmente. Y de hecho también es sencillo llevarlo a cabo si el binario es un string:
function reverse(x="0", width=0){
x = x.replace(/^0+/, "") || "0";
return [...x.padStart(width, "0")].reverse().join("");
}Lo anterior convierte el string en un array de caracteres y luego lo invierte usando el método reverse() de Array, volviendo a unir sus caracteres con el método join().
Para invertir un binario es importante especificar su ancho. Por ejemplo, si tenemos el binario 110 y aplicamos inversiones de varios anchos obtenemos números diferentes:
3 110 011 4 0110 0110 5 00110 01100 6 000110 011000
Implementamos reverse() con números de la siguiente forma:
function reverse(num=0, width=0) {
let reversed = 0;
for (let i=0; i<width; i++) {
let x = (num >>> i) & 1;
//También reversed += x * Math.pow(2, width-1-i);
reversed = x | (reversed << 1);
}
return reversed;
}Iteramos por los bits del ancho w (width en el código) tomando el bit que está a la derecha en cada paso y lo guardamos en x. Lo incorporamos por la izquierda de dos formas posibles. Una de ellas se basa en multiplicar ese bit x, que puede ser un cero o un uno, por la potencia del lugar de la izquierda x·2w-1-i. Si por ejemplo w = 8 y el primer bit de la derecha es un uno (posición i=0), entonces para situarlo a la izquierda hacemos 1·28-1-0 = 27 que es el binario r=10000000, ubicando el uno al inicio del ancho w=8. El siguiente bit, cero o uno, se multiplica por 26 y se suma al r obtenido antes. Y así sucesivamente. Esta forma es la que aparece en la línea en comentario del código anterior.
La segunda forma es desplazando el invertido r (reversed en el código) una posición a la izquierda y haciendo un OR con el bit extraído. Si tuviéramos en un momento dado del bucle r = 10101 y el siguiente bit extraído es un cero, entonces hacemos 1 | (r << 1) = 1 | (10101 << 1) = 1 | 101010 = 101011. Recuerde que el desplazamiento izquierda es sobre el registro de 32 bits de JavaScript.
La siguiente traza muestra como evoluciona el bucle para las dos opciones, obteniéndose al final del bucle el mismo binario:
n: 00110101 (num) w: 8 (width) r: 0 (reversed) x: (n >>> i) & 1 i x x|(r<<1) r+x·2w-1-i ----------------------------- 0 1 1 10000000 1 0 10 10000000 2 1 101 10100000 3 0 1010 10100000 4 1 10101 10101000 5 1 101011 10101100 6 0 1010110 10101100 7 0 10101100 10101100
Quizás es preferible la opción x | (reversed << 1) dado que la otra usa operaciones aritméticas que pueden ser más lentas.
Algoritmo CRC reflejado optimizado para JavaScript
En el primer apartado vimos como obtener el resto de una forma simplificada. Como ejemplo usamos la entrada index = 01111010, 0x7A en hexadecimal, 122 en decimal, letra "z" en ASCII. Y que el polinomio era 0x9B con un ancho w = 8 bits (CRC-8/LTE). Agregando el 1 inicial es poly = (1)10011011. Obteníamos el resultado de mod(08, poly, index) = mod(08, 110011011, 01111010) = 00101010 usando una simplificación del algoritmo donde prescindíamos del uno inicial del polinomio:
Poly 10011011 ⇒ 0x9B Trace for Index = 0b01111010, 0x7A, 122 : j=0 ⇒ 01111010 << 1 = 11110100 = 11110100 j=1 ⇒ 11110100 << 1 = 11101000 ^ Poly = 01110011 j=2 ⇒ 01110011 << 1 = 11100110 = 11100110 j=3 ⇒ 11100110 << 1 = 11001100 ^ Poly = 01010111 j=4 ⇒ 01010111 << 1 = 10101110 = 10101110 j=5 ⇒ 10101110 << 1 = 01011100 ^ Poly = 11000111 j=6 ⇒ 11000111 << 1 = 10001110 ^ Poly = 00010101 j=7 ⇒ 00010101 << 1 = 00101010 = 00101010
Si invertimos el polinomio sin el uno inicial tenemos Poly reversed = 11011001. Si invertimos la entrada tenemos Index reversed = 01011110. Si en lugar de utilizar el desplazamiento izquierda usamos el derecha, el algoritmo ejecutará esto:
Poly reversed 11011001 ⇒ 0xD9 Trace for Index reversed = 0b01011110, 0x5E, 94: j=0 ⇒ 01011110 >>> 1 = 00101111 = 00101111 j=1 ⇒ 00101111 >>> 1 = 00010111 ^ Poly = 11001110 j=2 ⇒ 11001110 >>> 1 = 01100111 = 01100111 j=3 ⇒ 01100111 >>> 1 = 00110011 ^ Poly = 11101010 j=4 ⇒ 11101010 >>> 1 = 01110101 = 01110101 j=5 ⇒ 01110101 >>> 1 = 00111010 ^ Poly = 11100011 j=6 ⇒ 11100011 >>> 1 = 01110001 ^ Poly = 10101000 j=7 ⇒ 10101000 >>> 1 = 01010100 = 01010100
Se observa la exacta simetría de ambos algoritmos. Cada resto parcial de esta ejecución con polinomio y entrada invertido es un fiel reflejo del de la ejecución sin inversión. Usamos desplazamientos a la derecha que son menos problemáticos en JavaScript. Además vemos que se suma XOR con el polinomio cuando el bit de la derecha es un uno (resaltados en amarillo), lo nos facilitará comprobar si ese bit es un uno.
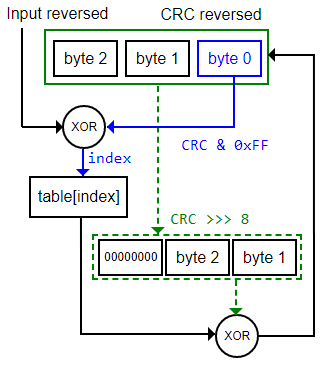
Apliquemos esto al algoritmo para obtener el CRC que se presenta esquemáticamente en la Figura. La entrada Input reversed es invertida, es decir, cada byte se invierte con reversed(Byte, 8) antes de tratarlo. El registro que contiene el CRC también está invertido, por lo que tomaremos el byte menos significativo o byte de la derecha como crcTopByte. Esto lo conseguimos con algo tan simple como CRC & 0xFF.
Hacemos, como antes, la suma XOR entre el byte y el index para obtener el valor de la tabla. Desplazamos 8 bits a la derecha el CRC y lo sumamos XOR con el resultado de la tabla, siendo este el nuevo valor del CRC para el siguiente byte de la entrada.
La implementación del algoritmo reflejado es la siguiente:
function crcTableReverseBasic({arrayBytes=[], width=0, poly="0"}){
let widthBits = Math.max(width, 8);
poly = reverse(Number(`0x${poly}`), width);
let table = [];
for (let i=0; i<256; i++){
let n = i;
for (let j=0; j<8; j++){
let shifted = n >>> 1;
if (n & 1===1) {
n = shifted ^ poly;
} else {
n = shifted;
}
}
table.push(n);
}
let crc = 0;
for (let i=0; i<arrayBytes.length; i++){
let Byte = reverse(arrayBytes[i], 8);
let crcTopByte = crc & 0xFF;
let index = crcTopByte ^ Byte;
let tab = table[index];
let crcShift = crc >>> 8;
crc = crcShift ^ tab;
}
crc = reverse(crc, width);
if (crc<0) crc += Math.pow(2, 32);
return crc;
}Compare la parte que genera la tabla con la versión anterior sin reflejar:
//Versión sin reflejar para generar la tabla
poly = Number(`0x${poly}`) * Math.pow(2, widthBits-width);
let table = [];
for (let i=0; i<256; i++){
let n = i * Math.pow(2, widthBits-8);
for (let j=0; j<8; j++){
let shifted = (n<<1) & (Math.pow(2, widthBits)-1);
if (n>>>(widthBits-1) & 1) {
n = shifted ^ poly;
} else {
n = shifted;
}
}
table.push(n);
}Ahora hay que invertir el polinomio, pero no es necesario multiplicarlo por Math.pow(2, widthBits-width) para ajustar los polinomios a múltiplos de 8, pues estos ceros agregados quedarán a la izquierda y se desprecian. De igual forma no necesitaremos multiplicar cada byte entre 0 y 255 por Math.pow(2, widthBits-8). Ni ajustar el desplazamiento izquierda pues tenemos un desplazamiento derecha. Y en lugar de detectar si el bit más significativo es un uno, detectaremos que el bit menos significativo sea un uno, lo que se hace con n & 1===1 de forma muy simple.
Compare el bucle que itera por los bytes de la entrada y las operaciones de salida que devuelven el CRC con la versión anterior sin reflejar:
//Versión sin reflejar del bucle de la entrada y devolución CRC
for (let i=0; i<arrayBytes.length; i++){
let Byte = arrayBytes[i];
let crcTopByte = crc >>> (widthBits-8);
let index = crcTopByte ^ Byte;
let tab = table[index];
let crcShift = (crc<<8) & (Math.pow(2, widthBits)-1);
crc = crcShift ^ tab;
}
if (crc<0) crc += Math.pow(2, 32);
crc = crc / Math.pow(2, widthBits-width);
return crc;Ahora hay que invertir el byte de la entrada, pero el crcTopByte es ahora el byte de la derecha del CRC, que se obtiene fácilmente con crc & 0xFF. Ni hay que ajustar el desplazamiento a la izquierda para obtener crcShift, pues ahora es un desplazamiento derecha. Con la versión reflejada antes de devolver el CRC tenemos que invertirlo para deshacer el reflejo del algoritmo. Pero no necesitamos deshacer el agregado de ceros como si hacemos en la versión sin reflejar.
Las operaciones con la versión reflejada son más simples. El único inconveniente es invertir con reverse() el polinomio, cada byte de la entrada y el CRC final. En un tema posterior veremos que esto es una ventaja en ciertos casos.
Veamos la ejecución de un ejemplo que ya hemos visto con los dos algoritmos anteriores de este tema. Se trata del CRC-24/LTE-A, polinomio de ancho w=24 bits, usando la entrada "123456789", presentando sólo la iteración del tercer byte (i=2):
i=2 ⇒ byte = arrayBytes[2] = 00110011 ⇒ byte = reverse(byte) = 11001100
crcTopByte = crc & 0xFF = 100010010011000111101101 & 11111111 = 11101101
index = byte ^ crcTopByte = 11001100 ^ 11101101 = 00100001
tab = table[index] = 101000101000010100000101
crcShift = crc >>> 8 = 100010010011000111101101 >>> 8 = 000000001000100100110001
crc = crcShift ^ tab = 000000001000100100110001 ^ 101000101000010100000101 =
101000100000110000110100 ⇒ 0xA20C34Si invertimos este resultado parcial reverse(101000100000110000110100, 24) obtendremos el mismo CRC parcial 0x2C3045 que con los dos algoritmos anteriores vistos en este tema.
El interior del bucle que itera por los bytes de la entrada puede simplificarse en una única línea con crc = (crc >>> 8) ^ table[Byte ^ (crc & 0xFF)], donde el byte es invertido previamente y el CRC es también el invertido. Si vemos algo como esto cuando empezamos a estudiar como funcionan los algoritmos para generar el CRC nos sentiremos algo confusos, tal como expusimos al inicio de esta serie de temas. Ahora ya estamos en condiciones de entenderlo.
Pero la cosa no acaba aquí. Aún nos falta un siguiente tema, pues sobre este último algoritmo hay varias cosas más que necesitamos hacer.