Algoritmo reflejado para generar CRC hasta 32 bits

En los temas anteriores hemos visto algoritmos para generar el CRC que hemos denominado básicos. Todos ellos se ejecutaban con tres argumentos: el array de bytes del archivo (arrayBytes), el ancho del polinomio (width) y el polinomio (poly). Pero en los algoritmos finales hay que contemplar cuatro argumentos más: init, refin, refout y xorout. En este tema haremos una implementación final del algoritmo reflejado con todos los argumentos. Dado que JavaScript maneja números binarios sólo hasta 32 bits, haremos también otra versión para manejar polinomios de anchos superiores. Completaremos el tema comentando como verificar en el destino un mensaje que nos llegue con el CRC agregado al final.

En la ejecución de la herramienta Web Tools online podrá ejecutar el CRC-8/AUTOSAR con la entrada "123456789", ofreciéndose una traza de la ejecución de los siguientes algoritmos:

crcBytesBasic({arrayBytes, poly, width}) = 000111110 ⇒ 0x3E
crcBytesBasic2({arrayBytes, poly, width}) = 00111110 ⇒ 0x3E
crcBytesBasic3({arrayBytes, poly, width}) = 00111110 ⇒ 0x3E
crcTableStringBasic({arrayBytes, poly, width}) = 00111110 ⇒ 0x3E
crcTableBasic({arrayBytes, poly, width}) = 111110 ⇒ 0x3E
crcTableReverseBasic({arrayBytes, poly, width}) = 111110 ⇒ 0x3E
getCrc({arrayBytes, poly, width, init, refin, refout, xorout}) = 11011111 ⇒ 0xDF
getCrcArr({arrayBytes, poly, width, init, refin, refout, xorout}) = 11011111 ⇒ 0xDF

Los que contienen "Basic" en el nombre de la función son todos los que hemos visto en temas anteriores. Vease que se ejecuta con tres argumentos: el array de bytes arrayBytes, el polinomio poly y su ancho width. La función getCrc() que veremos a continuación tiene cuatro argumentos más: init, refin, refout y xorout. Al igual que la última getCrcArr() que veremos en un apartado siguiente, permitiéndonos generar CRC con polinomios superiores a 32 bits. Con los básicos obtenemos el mismo resultado, que difiere de los dos últimos, pues algunos de esos nuevos argumentos modifican el proceso de generación del CRC. Primero veamos como se implementa getCrc() y luego explicaremos esos nuevos argumentos.

function getCrc({arrayBytes=[], width=0, poly="0",
init="0", refin=false, refout=false, xorout="0"}){ // (*)
    poly = reverse(Number(`0x${poly}`), width);
    init = reverse(Number(`0x${init}`), width); // (*)
    xorout = Number(`0x${xorout}`); // (*)
    let crc = init; // (*)
    let table = [];
    for (let i=0; i<256; i++){
        let n = i;
        for (let j=0; j<8; j++){
            let shifted = n >>> 1;
            if (n & 1===1) {
                n = shifted ^ poly;
            } else {
                n = shifted;
            }
        }
        table.push(n);
    }
    for (let i=0; i<arrayBytes.length; i++){
        let Byte = arrayBytes[i];
        if (!refin) Byte = reverse(Byte, 8); // (*)
        let crcTopByte = crc & 0xFF;
        let index = crcTopByte ^ Byte;
        let tab = table[index];
        let crcShift = crc >>> 8;
        crc = crcShift ^ tab;
    }
    if (!refout) crc = reverse(crc, width); // (*)
    crc = crc ^ xorout; // (*)
    if (crc<0) crc += Math.pow(2, 32);
    return crc;
}

Este algoritmo puede generar CRC con ancho hasta 32 bits. Es el algoritmo crcTableReverseBasic() visto al final del tema anterior, más lo que afecta a los nuevos argumentos. Son las líneas nuevas que hemos marcado con (*). En los siguientes apartados explicaremos estos nuevos argumentos.

En la herramienta Web Tools online podemos ejecutar la función getCrcTableReverse(), que es la misma que getCrc() del código anterior, pero conteniendo código para producir una traza. Veamos esa traza con el generador CRC-8/AUTOSAR usando la entrada "z", donde resaltamos el uso de esos nuevos argumentos.

getCrcTableReverse({arrayBytes, width, poly, init, refin, refout, xorout})
Input: z ⇒ arrayBytes = [01111010]
Width: 8
Poly: 0x2F ⇒ (1) 00101111
Poly reversed without (1):  11110100 ⇒  0xF4
Init: 0xFF ⇒  11111111
Init reversed:  11111111 ⇒  0xFF
Refin: false
Refout: false
Xorout: 0xFF ⇒  11111111

GENERATE TABLE with Poly reversed  0xF4
index = 000 =  00000000 table[000] =  00000000 ⇒  0x00
index = 001 =  00000001 table[001] =  11000111 ⇒  0xC7
index = 002 =  00000010 table[002] =  01100111 ⇒  0x67
······
index = 133 =  10000101 table[133] =  11111101 ⇒  0xFD 
······
index = 161 =  10100001 table[161] =  00001110 ⇒  0x0E (First byte of Input)
······
index = 253 =  11111101 table[253] =  00100101 ⇒  0x25
index = 254 =  11111110 table[254] =  10000101 ⇒  0x85
index = 255 =  11111111 table[255] =  01000010 ⇒  0x42

Trace for index=161 ⇒  0xA1: 
j=0 ⇒  10100001 >>> 1 =  01010000 ^ Poly =  10100100
j=1 ⇒  10100100 >>> 1 =  01010010        =  01010010
j=2 ⇒  01010010 >>> 1 =  00101001        =  00101001
j=3 ⇒  00101001 >>> 1 =  00010100 ^ Poly =  11100000
j=4 ⇒  11100000 >>> 1 =  01110000        =  01110000
j=5 ⇒  01110000 >>> 1 =  00111000        =  00111000
j=6 ⇒  00111000 >>> 1 =  00011100        =  00011100
j=7 ⇒  00011100 >>> 1 =  00001110        =  00001110

crc = Init = reverse(Init) =  11111111


INPUT LOOP using Poly of 8 bits
i=0 ⇒ byte = arrayBytes[0] =  01111010 ⇒ Refin = false  ⇒ byte = reverse(byte) =  01011110
crcTopByte = crc & 0xFF =  11111111 &  11111111 =  11111111
index = byte ^ crcTopByte =  01011110 ^  11111111 =  10100001 ⇒ 0xA1 (161)
tab = table[index] =  00001110
crcShift = crc >>> 8 =  11111111 >>> 8 =  00000000
crc = crcShift ^ tab =  00000000 ^  00001110 =  00001110 ⇒  0x0E

Refout = true  ⇒  crc = reverse(crc) =  01110000 ⇒  0x70

Residue:  01110000 ⇒  0x70
CRC final = crc ^ Xorout =  01110000 ^  11111111 =  10001111 ⇒  0x8F

Observe que refin y refout son falsos, por lo que hay que invertir los bytes de la entrada y el CRC de salida dado que estamos usando el algoritmo reflejado. En la traza se abrevia la generación de la tabla, ofreciendo un detalle de la traza para el índice del primer byte de la entrada (en color azul).

Reflejando la entrada y/o salida del CRC

Los nuevos argumentos booleanos Refin y Refout imponen si reflejamos la entrada y/o la salida respectivamente. Usualmente ambos son verdadero o ambos son falso a la vez, pero hay que prever la posibilidad de otras combinaciones. De hecho existe el CRC-12/UMTS donde el primero es falso y el segundo verdadero. Con ambos valor verdadero se reflejará cada byte de la entrada y el CRC de salida en un algoritmo no reflejado. Pero dado que estamos usando el algoritmo reflejado, cuando refin = true y refout = true no necesitamos invertir el byte ni el CRC de salida, pues ese algoritmo nos dará el CRC invertido. Cuando ambos son falso, el algoritmo se comporta como el visto en el tema anterior, siendo necesario invertir los bytes y el CRC de salida.

Esa es la ventaja que habíamos comentado en el tema anterior para el algoritmo reflejado. Por ejemplo, el CRC-32/ISO-HDLC usa refin = true y refout = true, con lo que no necesita invertir la salida ni los bytes. Esto último es lo realmente importante, puesto que invertir cada byte de un archivo muy grande puede disminuir la eficiencia.

Detectando bytes cero iniciales y finales agregados durante la transmisión

Veamos ahora los nuevos argumentos Init y Xorout. En el apartado Generando CRC con resto de la división vimos el ejemplo con la entrada "z" cuyo valor binario es 01111010. Usábamos el divisor 1011. Se agregaba la longitud menos uno del divisor, tres ceros, para obtener la entrada aumentada 1111010000. Obteníamos el resto con la división en aritmética Mod2, donde se usa el operador XOR (^) en lugar de la resta en la división en arimética normal:

 1111010000  │ 1011
             └─────────
               1101100
^1011
 ────
 01000
^ 1011
 ─────
 0001110
^   1011
 ───────
 00001010
^    1011
 ────────
 0000000100

Obteníamos el resto 100. Los ceros que pongamos a la izquierda de la entrada 01111010 no modifican ese resultado. Pues en cualquier aritmética los ceros iniciales siempre serán ignorados. Pero recordemos que estamos verificando un mensaje que por algún motivo pudiera añadir erróneamente ceros iniciales. Eso sería un error no detectable a no ser que inicialicemos el CRC on un valor inicial distinto de cero. En el código de nuestro algoritmo vemos la línea let crc = init, que en los algoritmos anteriores se inicializaba con valor cero.

Veamos el ejemplo del CRC-3/ROHC con poly: 0x3, width: 3, init: 0x7, refin: true, refout: true y xorout: 0. Con la entrada "123456789", cuyo array de bytes en hexadecimal es [0x31, 0x32, 0x33, 0x34, 0x35, 0x36, 0x37, 0x38, 0x39], obtenemos un CRC 0x6. Pero si anteponemos dos bytes cero [0x00, 0x00, 0x31, 0x32, ...] el resultado del CRC es 0x3 distinto del anterior. Así imponiendo el valor de inicio 0x7 detectamos cuando hay ceros iniciales no deseados.

El generador CRC-32/ISO-HDLC usa init: 0xFFFFFFFF y xorout: 0xFFFFFFFF. Pero estos dos argumentos no tienen porque ser iguales. El segundo xorout realiza una suma XOR con el CRC antes de devolverlo. Tiene el cometido de detectar ceros finales en la entrada agregados erróneamente que, con algunos polinomios y algunas entradas, pudieran no ser detectadas. Sucederá cuando la entrada más los ceros agregados en el camino compongan un número que sea un múltiplo del polinomio, pues en ese caso la comprobación en el destino será cero, originando por tanto un falso positivo.

Veamos un ejemplo con la entrada "z", binario 01111010 y polinomio 1011, cuyo CRC es 100. Agregamos el CRC a la entrada y aplicamos MOD en la recepción para comprobar si obtenemos un cero:

Recepción:
01111010100 MOD 1011 ⇒ 
      0000    01111010100
k= 0  0000    1111010100
k= 1  0001    111010100
k= 2  0011    11010100
k= 3  0111    1010100
k= 4  1111    010100
      1111 XOR 1011 = 0100
k= 5  1000    10100
      1000 XOR 1011 = 0011
k= 6  0111    0100
k= 7  1110    100
      1110 XOR 1011 = 0101
k= 8  1011    00
      1011 XOR 1011 = 0000
k= 9  0000    0
k=10  0000 Ok

Se obtuvo un resto cero, con lo que el mensaje recibido es correcto. Pero supongamos que en la transmisión se agrega un cero final, resaltado en azul en la siguiente traza:

Recepción:
011110101000 MOD 1011 ⇒ 
      0000    011110101000
k= 0  0000    11110101000
k= 1  0001    1110101000
k= 2  0011    110101000
k= 3  0111    10101000
k= 4  1111    0101000
      1111 XOR 1011 = 0100
k= 5  1000    101000
      1000 XOR 1011 = 0011
k= 6  0111    01000
k= 7  1110    1000
      1110 XOR 1011 = 0101
k= 8  1011    000
      1011 XOR 1011 = 0000
k= 9  0000    00
k=10  0000    0
k=11  0000: Falso positivo!!!

Se observa que se obtiene también cero, siendo un falso positivo pues el mensaje recibido no es el que se transmitió originalmente. Si en la generación del CRC 100 antes de devolverlo sumamos XOR con 111, el CRC pasa a ser 011. Transmitimos el mensaje con este CRC y en la recepción obtenemos un cero, aplicando también el XOR con 111 como se hizo en la generación:

Generación:
CRC ^ Xorout = 100 ^ 111 = 011

Recepción:
01111010011 MOD 1011 ⇒ 
      0000    01111010011
k= 0  0000    1111010011
k= 1  0001    111010011
k= 2  0011    11010011
k= 3  0111    1010011
k= 4  1111    010011
      1111 XOR 1011 = 0100
k= 5  1000    10011
      1000 XOR 1011 = 0011
k= 6  0111    0011
k= 7  1110    011
      1110 XOR 1011 = 0101
k= 8  1010    11
      1010 XOR 1011 = 0001
k= 9  0011    1
k=10  0111 ^ Xorout = 111 ^ 111 = 000 Ok

En este caso un cero agregado en la transmisión si será detectado:

Recepción:
011110100110 MOD 1011 ⇒ 
      0000    011110100110
k= 0  0000    11110100110
k= 1  0001    1110100110
k= 2  0011    110100110
k= 3  0111    10100110
k= 4  1111    0100110
      1111 XOR 1011 = 0100
k= 5  1000    100110
      1000 XOR 1011 = 0011
k= 6  0111    00110
k= 7  1110    0110
      1110 XOR 1011 = 0101
k= 8  1010    110
      1010 XOR 1011 = 0001
k= 9  0011    10
k=10  0111    0
k=11  1110
      1110 XOR 1011 = 0101 ^ Xorout = 101 ^ 111 = 010 ≠ 000 
      ⇒ Detectó ceros finales

Algoritmo reflejado para CRC mayores de 32 bits

Los últimos algoritmos que hemos visto, incluido el del apartado anterior, se ejecutan con números binarios en JavaScript. Estos tienen una capacidad hasta 32 bits. Polinomios de anchos superiores no pueden ser tratados con esos algoritmos. En las versiones que hicimos con binarios en string si podíamos utilizar anchos de polinomio sin limitación. Veamos ahora si es posible hacer lo mismo usando números binarios.

El generador CRC-82/DARC tiene un ancho de 82 bits usando el polinomio 0x0308C0111011401440411. Para manejar polinomios mayores de 32 bits vamos a desglosar el número en un array. Será necesario preparar algunas funciones accesorias previas para poder adaptar el algoritmo del CRC del apartado anterior para que funcione con arrays de números. Empecemos con esta función que recibe un número hexadecimal en string y nos lo devuelve en un array con trozos de 32 bits:

function hexToArrNum(hex="0"){
    hex = hex.padStart(8*Math.ceil(hex.length/8), "0");
    let arr = [];
    for (let i=hex.length-1; i>-1; i-=8){
        let num = Number(`0x${hex.substr(i-7, 8)}`);
        arr.push(num);
    }
    return arr;
}

Pasando el string "0308C0111011401440411" obtenemos el array de números [0x01440411, 0x01110114, 0x0000308C]. Observe que el trozo de 32 bits menos significativo se ubica al principio del array. Necesitaremos una función similar que reciba un binario en string y nos devuelva un array de números:

function binToArrNum(bin="0"){
    bin = bin.padStart(32*Math.ceil(bin.length/32), "0");
    let arr = [];
    for (let i=bin.length-1; i>-1; i-=32){
        let num = Number(`0b${bin.substr(i-31, 32)}`);
        arr.push(num);
    }
    return arr;
}

La función siguiente hace lo contrario, traspasa un array de números a un binario en string:

function arrNumToStr(num=[]) {
    return num.reverse().map(v => (v<0 ? v+Math.pow(2,32) : v).
    toString(2).padStart(32, "0")).join("").replace(/^0+/, "").
    replace(/^(?:)$/, "0");
}

El algoritmo necesita hacer desplazamientos a la derecha. Usaremos la siguiente función que se ejecuta completamente con números binarios:

function shiftRightArrNum(num=[], shift=0){
    return num.map((v, k, a) => (v >>> shift) |
    (k<a.length-1 ? (a[k+1] & (Math.pow(2, shift)-1)) *
    Math.pow(2, 32-shift) : 0));
}

Y también hace falta invertir números. La función siguiente se encarga de eso. Si el número es menor o igual que 32 bits usaremos la función reverse() que ya utilizamos anteriormente y que funciona sobre números. Si es mayor de 32 bits convertiremos el array de números en un string y los invertiremos con reverseStr() que tambien hemos utilizado y que trabaja con binarios en string. El resultado se convierte en un array de números con binToArrNum() que vimos antes. No es la solución ideal pues sería preferible hacer la inversión con números. Probablemente es posible hacerlo, pero por ahora no quiero complicarlo más y lo dejaré así.

function reverseArrNum(num=[], width=0){
    if (width>32) {
        let numStr = arrNumToStr(num);
        return binToArrNum(reverseStr(numStr, width));
    } else {
        return [reverse(num[0], width)];
    }
}

Por último usaremos la siguiente función que suma XOR dos arrays de números:

function xorArrNum(x=[], y=[]){
    return x.map((v, k) => v ^ y[k]);
}

Con todo lo anterior pasamos ya a implementar getCrcArr() que genera el CRC para cualquier ancho de polinomio. Es el mismo algoritmo del apartado anterior, sólo que ahora trabajamos con arrays de números:

function getCrcArr({arrayBytes=[], width=0, poly="0",
init="0", refin=true, refout=true, xorout="0"}){
    poly = reverseArrNum(hexToArrNum(poly), width);
    init = reverseArrNum(hexToArrNum(init), width);
    xorout = hexToArrNum(xorout);
    let crc = init;
    let table = [];
    for (let i=0; i<256; i++){
        let n = Array.from({length: poly.length}, (v,k) => k===0 ? i : 0);
        for (let j=0; j<8; j++){
            let shifted = shiftRightArrNum(n, 1);
            if (n[0] & 1===1) {
                n = xorArrNum(shifted, poly);
            } else {
                n = [...shifted];
            }
        }
        table.push(n);
    }
    for (let i=0; i<arrayBytes.length; i++){
        let Byte = arrayBytes[i];
        if (!refin) Byte = reverse(Byte, 8);
        let crcTopByte = crc[0] & 0xFF;
        let index = crcTopByte ^ Byte;
        let tab = table[index];
        let crcShift = shiftRightArrNum(crc, 8);
        crc = xorArrNum(crcShift, tab);
    }
    if (!refout) crc = reverseArrNum(crc, width);
    let residue = crc;
    crc = xorArrNum(crc, xorout);
    return [arrNumToStr(crc), arrNumToStr(residue)];
}

Poco más hay que comentar de este algoritmo que es el mismo que el del apartado anterior. Sólo observar la facilidad para comprobar que el bit menos significativo es un uno cuando generamos la tabla. Y también como obtenemos el crcTopByte que es el byte menos significativo. En ambos casos lo hacemos sobre la posición cero del array pues ahí se encuentra el trozo de 32 bits menos significativo. La suma entre el byte y el crcTopByte se hace con el XOR de JavaScript pues ambos tienen longitud 8 bits.

Al final devolvemos el array de números CRC como binario en string, donde la función arrNumToStr() ya contempla la posibilidad de que algunos items del array sean números negativos, en cuyo caso le suma Math.pow(2,32) tal como hicimos en anteriores algoritmos. Y también devolvemos el residuo, ambas cosas en un array. El cometido del residuo, que veremos en un apartado posterior, es verificar en la recepción la corrección del mensaje.

Catálogo de algoritmos CRC parametrizados

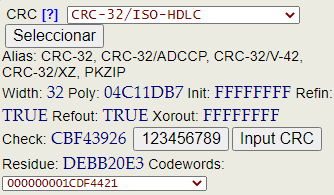
La web Catalogue of parametrised CRC algorithms contiene una lista de 107 generadores CRC desde un ancho de 3 bits hasta 82 bits. Agradezco enormemente la existencia de este catálogo, pues me ha permitido comprobar el correcto funcionamiento de los distintos algoritmos que he usado para estos temas. He tomado las definiciones de esa página para incluirlas en la herramienta, tal como se observa en la Figura. Al seleccionar el CRC obtenemos los parámetros Width, Poly, Init, Refin, Refout y Xorout. Y también Check, Residue y Codewords que explicaremos a continuación. A excepción del ancho Width que es un decimal y Refin y Refout que son booleanos, el resto son valores hexadecimales.

El catálogo se incluye como un objeto en la herramienta. Por ejemplo, la entrada del polinomio CRC-32/ISO-HDLC que aparece en la imagen anterior es como sigue:

// Catalogue of parametrised CRC algorithms
// https://reveng.sourceforge.io/crc-catalogue/all.htm
// Greg Cook
// Released under the terms of the GNU General Public License (GPLv3+)
...
"CRC-32/ISO-HDLC": {
    alias: "CRC-32, CRC-32/ADCCP, CRC-32/V-42, CRC-32/XZ, PKZIP",
    width:32,
    poly:"04c11db7",
    init:"ffffffff",
    refin:true,
    refout:true,
    xorout:"ffffffff",
    check:"cbf43926",
    residue:"debb20e3",
    codewords: [
        "000000001CDF4421",
        "F20183779DAB24",
        "0FAA005587B2C9B6",
        "00FF55111262A032",
        "332255AABBCCDDEEFF3D86AEB0",
        "926B559BA2DE9C",
        "FFFFFFFFFFFFFFFF"
    ]
},
...

En la herramienta encontrará el botón con el icono que le permitirá descargar el catálogo actualizado, o bien descargar aquí la versión vigente cuando elaboré este tema con este enlace catálogo crc.

El parámetro residue del catálogo sirve para verificar la correcta transmisión en el destino, como veremos en un apartado posterior. Mientras desarrollamos nos puede servir para verificar la correcta ejecución utilizando algunos de los codewords como entrada. Con CRC-32/ISO-HDLC usando el primer codeword de la lista 000000001CDF4421 obtenemos el siguiente resultado:

getCrcTable()
Residue: #11011110101110110010000011100011 ⇒ #0xDEBB20E3
CRC....:  00100001010001001101111100011100 ⇒  0x2144DF1C
Time: 3 ms

Observe que Residue = 0xDEBB20E3 el mismo que aparece en la definición del catálogo. El residuo es el CRC antes de aplicar el xorout.

El parámetro Check nos da el CRC que se obtendría con la entrada "123456789". Disponemos de un botón que genera esa entrada. Así que este catálogo contiene los valores Check que nos sirve para comprobar la correcta ejecución en la implementación de los siguientes algoritmos, que puede ejecutar en la herramienta y que se exponen en estos temas:

Podemos comprobar que todas las definiciones se ejecutan correctamente, generándose un informe como el siguiente, donde sólo ponemos el primero de 3 bits, uno de 32 bits y el último de 82 bits:

CRC-3/GSM check=4 Total check: [1]
    DivMod2: 4 [1]
    ModMod2: 4 [1]
    Bytes: 4 [1]
    Bytes2: 4 [1]
    Bytes3: 4 [1]
    TableString: 4 [1]
    Table: 4 [1]
    TableReverse: 4 [1]
    getCrc: 4 [1]
    getCrcArr: 4 [1]
...
CRC-32/ISO-HDLC check=CBF43926 Total check: [1]
    DivMod2: CBF43926 [1]
    ModMod2: CBF43926 [1]
    Bytes: CBF43926 [1]
    Bytes2: CBF43926 [1]
    Bytes3: CBF43926 [1]
    TableString: CBF43926 [1]
    Table: CBF43926 [1]
    TableReverse: CBF43926 [1]
    getCrc: CBF43926 [1]
    getCrcArr: CBF43926 [1]
...
CRC-82/DARC check=09EA83F625023801FD612  Total check: [1]
    DivMod2: 09EA83F625023801FD612 [1]
    ModMod2: 09EA83F625023801FD612 [1]
    Bytes: 09EA83F625023801FD612 [1]
    Bytes2: 09EA83F625023801FD612 [1]
    Bytes3: 09EA83F625023801FD612 [1]
    TableString: 09EA83F625023801FD612 [1]
    Table: ERROR width>32 [1]
    TableReverse: ERROR width>32 [1]
    getCrc: ERROR width>32 [1]
    getCrcArr: 09EA83F625023801FD612 [1]

Total 107 ok:107 not ok: 0
(6 items with Poly > 32 bits where functions Table, TableReverse
and getCrc do not work.)

También se ejecutan las versiones usando los algoritmos de la división DivMod2 y del resto ModMod2, tal como expusimos en el primer tema. Si en cada algoritmo se obtiene un CRC igual al Check marcamos con un [1], en otro caso pondríamos un [0]. Si todas las funciones originan uno entonces el total check será uno. Si el CRC tiene más de 32 bits, las ejecuciones de las versiones Table, TableReverse y getCrc que trabajan con números causarán error por exceso de bits, pero no lo consideramos un error de implementación. Hay 6 definiciones que son mayores de 32 bits. La función getCrcArr() no tiene limitación en cuanto al tamaño del polinomio. Las funciones getCrc y getCrcArr() son la que exponemos en este mismo tema.

También se comparan todos los algoritmos básicos que hemos visto en temas anteriores. En estos casos sólo usamos los parámetros Width y Poly, con lo que la revisión consiste en que todos obtengan el mismo CRC. Esta es una muestra del informe donde sólo incluimos el CRC-32/ISO-HDLC de 32 bits para no alargarnos demasiado:

...
CRC-32/ISO-HDLC Check: true
    crcBytesBasic: 89A1897F
    crcBytesBasic2: 89A1897F
    crcBytesBasic3: 89A1897F
    crcTableStringBasic: 89A1897F
    crcTableBasic: 89A1897F
    crcTableReverseBasic: 89A1897F
...
Total 107 ok: 107 not ok: 0
(6 items with Poly > 32 bits where functions crcTableBasic and 
crcTableReverseBasic do not work.)
    

En la herramienta podrá descargar ese informe, o bien descargar aquí la versión vigente cuando elaboré este tema con este enlace Compara crc.

Comprobando que el mensaje con el CRC agregado genera un resto cero

Todos los algoritmos que hemos presentado están preparados para generar el CRC a partir de una entrada. Este CRC se genera y agrega al mensaje antes de su transmisión. En la recepción tiene que haber otro algoritmo para comprobar que el CRC del mensaje que se recibe es cero. Si uno agrega el CRC a un mensaje pretendiendo obtener un CRC cero con los algoritmos vistos verá que no es posible, pues los algoritmos anteriores están preparados para agregar un aumento de la entrada con tantos ceros como el ancho del polinomio. La concatenación de entrada + CRC + 00..00 no ha de ser necesariamente un múltiplo del polinomio y, por lo tanto, no tiene porque ser cero.

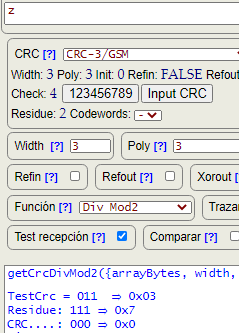
Para comprobar un CRC en la recepción podemos usar la herramienta Calculadora Binaria en Web Tools online. Como se observa en la Figura, usamos el generador CRC-3/GSM en la herramienta, marcando la casilla Test recepción. La entrada es la letra "z", con binario 01111010. Sólo es posible usar la comprobación en la recepción con las funciones DivMod2 y ModMod2, en las cuales se ha previsto que en lugar de aumentar la entrada con ceros lo haga con el CRC a comprobar, para lo cual se pasa un argumento testCrc que es ese CRC a comprobar. Se genera un CRC 011 para la entrada "z". Veamos una traza de la comprobación:

getCrcModMod2({arrayBytes, width, poly, init, refin, refout, xorout, testCrc})

Input: z ⇒ arrayBytes = [01111010]
Width: 3
Poly: 0x3 ⇒ (1)011
Init: 0x0 ⇒ 000
Refin: false
Refout: false
Xorout: 0x7 ⇒ 111
TestCrc = 011  ⇒ 0x03

Input = 01111010 
Augmented = TestCrc = 011 ⇒ 0x03

En lo anterior vemos los argumentos de la función incluyendo el testCrc que vamos a comprobar. La entrada es 01111010 y el aumento de la entrada que vamos a aplicar es ese CRC 011. El primer paso es aplicar el argumento Refin, que si fuera verdadero refleja la entrada. En este caso no lo es. Es tras esto cuando aumentamos la entrada con el CRC a comprobar:

A) Refin == false ⇒ InputRefin = Input ⇒ 01111010
TestCrc ⇒ inputRefinAugmented = 01111010011

El siguiente paso es sumar XOR con el argumento Init. En este caso es cero y no modifica la entrada aumentada:

B) InputInitAugmented = InputRefinAugmented XOR Init ⇒
01111010011
00000000000
───────────
01111010011

A continuación procedemos a generar el CRC usando el algoritmo MOD:

C) Residue = InputInitAugmented MOD Poly ⇒
 
01111010011 MOD 1011 ⇒ 
      0000    01111010011
k= 0  0000    1111010011
k= 1  0001    111010011
k= 2  0011    11010011
k= 3  0111    1010011
k= 4  1111    010011
      1111 XOR 1011 = 0100
k= 5  1000    10011
      1000 XOR 1011 = 0011
k= 6  0111    0011
k= 7  1110    011
      1110 XOR 1011 = 0101
k= 8  1010    11
      1010 XOR 1011 = 0001
k= 9  0011    1
k=10  0111
 
01111010011 MOD 1011 = 111

Obtenemos 111 y finalmente ejecutamos Refout que refleja la salida, no produciendo efecto en este caso pues refout = false.

D) Refout == false ⇒ ResidueRefout = Residue ⇒
111

El último paso es sumar XOR con Xorout, lo que produce un resultado cero verificándose que el mensaje no contiene modificaciones:

E) CRC = ResidueRefout XOR Xorout ⇒
111
111
──────
000 ⇒ 0x0

En la herramienta puede generarse un informe con la comprobación de los 107 generadores CRC del catálogo que estamos usando. Se utiliza la entrada "123456789" y el CRC Check que define el catálogo. Se obtiene cero en todos los casos. A continuación se expone ese informe, exponiendo sólo algunas líneas para no alargarnos demasiado:

RECEPCIÓN: Comprobar Check con entrada "123456789" usando en la recepción 
getCrcModMod2({arrayBytes, width, poly, init, refin, refout, xorout, testCrc})
CRC-3/GSM ⇒ Check: 0x4 ⇒ TestCrc = Check = 0x04 ⇒ CRC = 0
···
CRC-8/BLUETOOTH ⇒ Check: 0x26 ⇒ refout ⇒ TestCrc = reversed(Check) = 0x64 ⇒ CRC = 0
···
CRC-12/UMTS ⇒ Check: 0xDAF ⇒ refout ⇒ TestCrc = reversed(Check) = 0x0F5B ⇒ CRC = 0
···
CRC-16/XMODEM ⇒ Check: 0x31C3 ⇒ TestCrc = Check = 0x31C3 ⇒ CRC = 0
···
CRC-24/LTE-A ⇒ Check: 0xCDE703 ⇒ TestCrc = Check = 0xCDE703 ⇒ CRC = 0
···
CRC-32/ISO-HDLC ⇒ Check: 0xCBF43926 ⇒ refout ⇒ TestCrc = reversed(Check) = 0x649C2FD3 ⇒
    CRC = 0
···
CRC-64/ECMA-182 ⇒ Check: 0x6C40DF5F0B497347 ⇒ TestCrc = Check = 0x6C40DF5F0B497347 ⇒
    CRC = 0
···
CRC-82/DARC ⇒ Check: 0x09EA83F625023801FD612 ⇒ refout ⇒ TestCrc = reversed(Check) = 
    0x0121AFE00710291BF055E4 ⇒ CRC = 0
Total 107 ok: 107 not ok: 0

Los generadores que usen refout = true reflejan la salida al generar el CRC. Tal como hace CRC-32/ISO-HDLC, donde el CRC 0xCBF43926 que es el Check de "123456789", se usará para esta comprobación invertido 0x649C2FD3. Pero ya veremos en el siguiente apartado que realmente no se transmite así, sino invirtiendo los bytes (no los bits) del CRC, transmitiéndose 0x2639F4CB, puesto que cualquier destinatario debe ser capaz de verificar el CRC con cualquier algoritmo de generación de CRC y no con los que usamos en este apartado getCrcDivMod2() o getCrcModMod2().

Verificando el mensaje en el destino con el número mágico

Uno de los parámetros de cada polinomio del catálogo es residue, también denominado número mágico (magic number). Su utilidad es verificar el mensaje en el destino usando un algoritmo cualquiera de generación de CRC. El residuo es el CRC antes de aplicar el último xorout. Podemos ejecutar un algoritmo cualquiera de los vistos con el mensaje agregándole el CRC y comprobar que el residuo es igual que el del parámetro residue o número mágico, que será siempre el mismo independientemente del mensaje. Por supuesto, siempre y cuando el mensaje con el CRC no se haya modificado durante la transmisión.

Pero antes de enviar el mensaje necesitamos agregarle el CRC. Y dependiendo de los parámetros habrá que ajustarlo primero. La siguiente función se encarga de eso. Trabajamos con binarios en string para simplificar el proceso, aunque en la práctica debería convertirse en una versión que trabaje con números. Una ventaja al trabajar con string es que nos permitirá actuar sobre polinomios con anchos superiores a 32 bits.

function getInputCrc({crcBin="", crcHex="", width=0, refin=false, refout=false, xorout="0"}){
    let crc = (crcHex ? wtCB.hexToBin(crcHex).valor: crcBin).padStart(width, "0");
    let widthBits = 8*Math.ceil(width/8);
    if (widthBits > width) {
        if (xorout.replace(/^0+/, "").replace(/^(?:)$/, "0")==="0") {
            crc = refout ? crc.padStart(widthBits, "0") : crc.padEnd(widthBits, "0");
        } else {
            xorout = wtCB.hexToBin(xorout).valor;
            let residue = wtCB.xor(crc, xorout.padStart(width, "0")).padStart(width, "0");
            crc = refout ? residue.padStart(widthBits, "0") : residue.padEnd(widthBits, "0");
            xorout = refout ? xorout.padEnd(widthBits, "0") : xorout.padStart(widthBits, "0");
            crc = wtCB.xor(crc, xorout).padStart(widthBits, "0");
        }
    }
    let crcArr = [...crc].reduce((p,v,i,a) => ((i+1)%8===0 ? p.push(a.slice(i-7, i+1).join("")) : null, p), []);
    if (refout) crcArr = crcArr.reverse();
    if (refout && !refin) crcArr = crcArr.map(v => wtCB.reverse(v, 8));
    crcArr = crcArr.map(v => wtCB.binToHex(v).valor.padStart(2, "0"));
    return crcArr;
}

La función recibe el CRC en binario o hexadecimal en string y los parámetros width, refin, refout y xorout. Consideremos primero el caso cuando el ancho width es un múltiplo de 8, donde widthBits===width y no se ejecuta if (widthBits > width).

En la herramienta usaremos el botón Input CRC para ejecutar la función anterior y agregar al mensaje el CRC a transmitir, tras lo cual ejecutaremos el CRC sobre ese mensaje aumentado para observar el residuo obtenido.

Supongamos el polinomio CRC-24/LTE-A, con residue = 0x0, width = 24, refin = false, refout = false y xorout = 0x0. Si usamos la entrada "123456789" y la pasamos a hexadecimal será 31 32 33 34 35 36 37 38 39 donde separamos cada byte con un espacio. Con esta entrada se genera el CRC 0xCDE703. Con este polinomio donde refin = false, refout = false y xorout = 0x0 sólo tenemos que agregar el CRC al final del mensaje 31 32 33 34 35 36 37 38 39 CD E7 03. Usando cualquier algoritmo como el simple getCrcDivMod2() vemos que obtenemos el residuo igual que el número mágico:

getCrcDivMod2({arrayBytes, width, poly, init, refin, refout, xorout})

Residue: 000000000000000000000000 ⇒ 0x0
CRC....: 000000000000000000000000 ⇒ 0x0
Time: 2 ms

Veamos ahora CRC-32/ISO-HDLC con residue = 0xDEBB20E3, width = 32, refin = true, refout = true y xorout = FFFFFFFF. Con la entrada "123456789" generamos el CRC CBF43926. Como refout = true invertimos bytes (no bits), y agregamos al mensaje 31 32 33 34 35 36 37 38 39 26 39 F4 CB obteniéndose el número mágico 0xDEBB20E3:

getCrcBytes3({arrayBytes, width, poly, init, refin, refout, xorout})

Residue: 11011110101110110010000011100011 ⇒ 0xDEBB20E3
CRC....: 100001010001001101111100011100 ⇒ 0x2144DF1C
Time: 5 ms

Esto es independiente del mensaje. Supongamos que el mensaje es "z" (7A en hexadecimal) con CRC 0x62D277AF con lo que transmitimos 7A AF 77 D2 62 comprobando en el destino el mismo número mágico:

getCrcBytes3({arrayBytes, width, poly, init, refin, refout, xorout})

Residue: 11011110101110110010000011100011 ⇒ 0xDEBB20E3
CRC....: 100001010001001101111100011100 ⇒ 0x2144DF1C
Time: 1 ms

Cuando el ancho del polinomio es un múltiplo de 8 sólo hemos de tener en cuenta el parámetro refout. Usualmente si refout es verdadero refin también lo será. En otro caso si refout = true y refin = false hemos de invertir también los bits de cada byte del CRC a transmitir. Es el caso del polinomio CRC-12/UMTS.

Cuando el polinomio no es un múltiplo de 8 entra en juego el parámetro xorout. Si es cero agregaremos ceros por la derecha o por la izquierda hasta completar widthBits según el valor de refout. Si xorout no es cero la cosa se complica. Dado que en la generación el CRC fue modificado con el xorout, tenemos que ajustar este CRC al ancho widthBits múltiplo de 8. Para ello quitamos el xorout para obtener el residuo previo al CRC y luego volvemos a aplicar el xorout con ambos términos ajustados al ancho widthBits.

El número mágico o residue no tiene nada de mágico. Si un polinomio tiene xorout igual a cero su número mágico será cero. Por ejemplo, con CRC-32/ISO-HDLC si ponemos xorout = 0 y usamos la entrada "123456789", se genera el CRC 0x340BC6D9. Transmitiendo el mensaje 31 32 33 34 35 36 37 38 39 D9 C6 0B 34 se verificará en el destino con un número mágico o residuo cero. Esto es lo esperable dado que la entrada más el CRC es un múltiplo del polinomio y por tanto el resto debe ser cero. El xorout distinto de cero cambia este comportamiento, pero todos los mensajes que sean múltiplos del polinomio generan el mismo residuo.

En la herramienta se realiza una comprobación de los 107 polinomios del catálogo, construyendo el mensaje con "123456789" y el CRC del Check usando la función anterior getInputCrc(). Luego verificamos con el algoritmo de generación de CRC getCrcArr() que se obtiene el número mágico o residue que especifica el catálogo. Se obtiene un informe como el siguiente, donde sólo ponemos la entrada del CRC-32/ISO-HDLC para abreviar:

RECEPCIÓN 2: Comprobar Check con entrada "123456789" usando en la recepción
getCrcArr({arrayBytes, width, poly, init, refin, refout, xorout})
...
CRC-32/ISO-HDLC ⇒
    Check: 0xCBF43926
    Refin: true
    Refout: true
    Xorout: 0xFFFFFFFF
    getInputCrc(): 0x2639F4CB
    RESIDUE: Expected 0xDEBB20E3 = Obtained 0xDEBB20E3 [1]
...

Implementación práctica de CRC-32/ISO-HDLC

Los algoritmos que hemos visto sirven para calcular el CRC de cualquier polinomio. Pero en la práctica sólo usaremos un polinomio en una determinada aplicación. Por ejemplo el polinomio CRC-32/ISO-HDLC es utilizado en los ZIP o PNG. Recordemos sus parámetros en el catálogo:

width: 32
poly: 04C11DB7
init: FFFFFFFF
refin: true
refout: true
xorout: FFFFFFFF
check: CBF43926
residue: DEBB20E3

Un algoritmo reflejado práctico para implementarlo es una simplificación de la función getCrc():

const table = [];
function crc32IsoHdlc(arrayBytes=[]){
    if (table.length===0) {
        for (let i=0; i<256; i++){
            let n = i;
            for (let j=0; j<8; j++){
                let shifted = n >>> 1;
                n = (n & 1===1) ? shifted ^ 0xEDB88320 : shifted;
            }
            table.push(n);
        }
    }
    let crc = 0xFFFFFFFF;
    for (let Byte of arrayBytes){
        crc = (crc >>> 8) ^ table[Byte ^ (crc & 0xFF)];
    }
    crc = crc ^ 0xFFFFFFFF;
    if (crc<0) crc += 0xFFFFFFFF + 1;
    return crc;
}

La tabla podría ser una constante global que inicialmente es un array vacío. La primera vez que se ejecuta el algoritmo rellenará esa tabla, omitiéndose en las siguientes ejecuciones. Los parámetros ya van incluidos en el algoritmo, por lo que sólo pasamos el array de bytes. Vease que el polinomio 0x04C11DB7 se incorpora ya invertido 0xEDB88320 pues estamos usando el algoritmo reflejado. Se simplifica el interior del bucle de bytes y se usan directamente los parámetros Init y Xorout, ambos con valor 0xFFFFFFFF. Como estamos usando el algoritmo reflejado, Refin y Refout no se aplican, es decir, no es necesario invertir bytes ni la salida.

Si el algoritmo se implementara en el destino para verificar el mensaje, quitaríamos la línea crc = crc ^ 0xFFFFFFFF que ejecuta el xorout y comprobaríamos que el residuo es igual que el número mágico:

function crc32IsoHdlc(arrayBytes=[]){
    ...
    for (let Byte of arrayBytes){
        crc = (crc >>> 8) ^ table[Byte ^ (crc & 0xFF)];
    }
    if (crc<0) crc += 0xFFFFFFFF + 1;
    return crc === 0xDEBB20E3;
}