Combinaciones con repetición
Combinaciones con repetición

Las combinaciones con repetición de una lista con n elementos distintos son todas las sublistas con k elementos no necesariamente distintos que se pueden extraer sin importar el orden. Se denotan como ((nk)), CR(n, k) y también como CRn,k.
En la Figura vemos todas las sublistas de longitud 3 generadas con la lista {a, b, c, d}, donde se concatenan las letras en las sublistas, obteniéndose CR(4, 3) = 20 combinaciones. Si fueran combinaciones sin repetición hubiesen sido solo C(4, 3) = 4 sublistas: abc, abd, acd, bcd.
El valor númerico se obtiene con:
| CR(n, k) = C(n+k-1, k) = | (n+k-1)! |
| k! (n-1)! |
El algoritmo básico que vimos en un tema anterior para obtener las combinaciones era la recurrencia para obtener el Triángulo de Pascal: C(n, k) = C(n-1, k-1) + C(n-1, k). En las combinaciones con repetición tenemos CR(n, k) = CR(n, k-1) + CR(n-1, k), que es bastante similar, diferenciándose en los términos resaltados. Usando la recurrencia del triángulo de Pascal podemos deducir esta:
El algoritmo que vamos a usar basado en esta recurrencia CR(n, k) = CR(n, k-1) + CR(n-1, k) es similar al que vimos para las combinaciones sin repetición:
// CR(n, k) = CR(n, k-1) + CR(n-1, k)
function combineR1(list=[], k=0, n=list.length, res=[], result=[], n0=list.length){
if (k===0){
result.push(copy(res));
} else if (n>0) {
res.push(list[n0-n]);
combineR1(list, k-1, n, res, result);
res.pop();
combineR1(list, k, n-1, res, result);
}
return result;
}Combinaciones con repetición: coste sin copia
Agregamos al algoritmo anterior instrucciones iter que nos permiten contar las iteraciones, valor que ha de coincidir con el coste que vamos a calcular en este apartado.
// CR(n, k) = CR(n, k-1) + CR(n-1, k)
function combineR1(list=[], k=0, n=list.length, res=[], result=[], n0=list.length){
if (k===0){
iter += 1;
if (withCopyCost) iter += res.length;
result.push(copy(res));
} else if (n===0) {
iter += 1;
} else {
iter += 1;
res.push(list[n0-n]);
combineR1(list, k-1, n, res, result);
res.pop();
combineR1(list, k, n-1, res, result);
}
return result;
}Si n=0 no se hace nada, sólo cuenta como una iteración. En otro caso con n>0 ponemos un elemento con push() en el resultado parcial, hacemos una llamada, lo quitamos con pop() y hacemos la otra llamada. Cuando k=0 tendremos una combinación en el resultado parcial que guardamos en el resultado final. Se debe copiar el resultado parcial. Plantemos la recurrencia de este algoritmo, obviando por ahora el coste de copiar el resultado parcial:
| T(n, k) = { | 1 | si k=0 ∨ n=0 |
| T(n, k-1) + T(n-1, k) + 1 | si n > 0 |
Evitamos los índices negativos y partimos de la siguiente definición:
Usaremos la función generadora siguiente:
Las condiciones iniciales son:
| Gn,0 (x, y) = ∑n≥0 T(n, 0) xn y0 = ∑n≥0 xn = | 1 |
| 1-x |
| G0,k (x, y) = ∑k≥0 T(0, k) x0 yk = ∑k≥0 yk = | 1 |
| 1-y |
Expresemos los términos con n+1 y k+1, en función de T(n, k):
| ∑n,k≥0 T(n+1, k+1) xn yk = | 1 | ( G(x, y) - | 1 | - | 1 | + 1 ) |
| xy | 1-x | 1-y |
| ∑n,k≥0 T(n, k+1) xn yk = | 1 | (G(x, y) - | 1 | ) |
| y | 1-x |
| ∑n,k≥0 T(n+1, k) xn yk = | 1 | (G(x, y) - | 1 | ) |
| x | 1-y |
Recordemos que la serie geométrica con dos variables es:
| 1 | = ∑n≥0 xn ∑k≥0 yk= ∑n,k≥0 xn yk |
| (1-x)(1-y) |
Multiplicamos cada término de la recurrencia T(n+1, k+1) = T(n+1, k) + T(n, k+1)+ 1 por xn yk y aplicamos sumas:
Identificamos [1], [2], [3], [4] y [5]:
| 1 | ( G(x, y) - | 1 | - | 1 | + 1 ) | = |
| xy | 1-x | 1-y |
| = | 1 | (G(x, y) - | 1 | ) | + | 1 | (G(x, y) - | 1 | ) | + | 1 |
| y | 1-x | x | 1-y | (1-x)(1-y) |
Despejando G(x, y), queda lo siguiente (comprobar en Wolframalpha)
| G(x, y) = | 2xy-x-y+1 |
| (1-x)(1-y)(1-x-y) |
Descomponemos en fracciones simples
| G(x, y) = | 2xy-x-y+1 | = | 2 | - | 1 |
| (1-x)(1-y)(1-x-y) | 1-x-y | (1-x)(1-y) |
El término de la derecha es la serie geométrica, con lo que hemos de buscar la serie que corresponde al polinomio 2 / (1-x-y). Si nos centramos en el polinomio 1/(1-x-y) vemos en Wolframalpha este resultado, que puede comprobar en el desplegable con el desarrollo de Taylor:
| 1 | = ∑n≥0 | xn |
| 1-x-y | (1-y)n+1 |
Para reducir esto a algo más simple hemos de conocer los principios de las series binomiales:
La primera nos resulta familiar, pues es la aplicación del Binomio de Newton que hemos aplicado en los temas anteriores:
Con x=1 llegamos al resultado (1+y)n = ∑j=0..n C(n, j) y j. Recordemos que cuando j>n entonces C(n, j) = 0, por lo que el rango j=0..n puede sustituirse por j≥0 sin pérdida de generalidad.
La que nos puede ofrecer más dudas es la segunda. En la misma página del enlace anterior vemos el teorema del binomio generalizado de Newton, que referencia otra página titulada series binomiales negativas, que expone lo siguiente (cambiando nombres de variables x = y, k = j para luego no confudirlas con las que necesitaremos en nuestra serie):
Para llegar a un resultado donde podamos asimilar estos conceptos, en primer lugar vemos que a nuestra expresión [8] le falta el sumatorio en yk, intentaremos arreglarlo multiplicando y dividiendo por 1-y:
| 1 | = | 1-y | = | 1 | × | 1-y |
| 1-x-y | (1-y)(1-x-y) | 1-y | 1-x-y |
Si ahora separamos esto en dos multiplicandos, el de la izquierda 1/(1-y) es la serie geométrica ∑k≥0 yk. Mientras que el de la derecha tiene este resultado según vemos en Wolframalpha (el desarrollo de Taylor es similar al visto antes):
| 1-y | = ∑n≥0 | xn |
| 1-x-y | (1-y)n |
Por lo tanto
| 1 | = ∑n,k≥0 | 1 | xn yk |
| 1-x-y | (1-y)n |
Tenemos ahora una serie con índices n, k que vamos a intentar simplificar con el concepto de serie binominal negativa [9] cambiando y = -y, a = 1
Observe la relación que hay con las combinaciones con repetición puesto que lo anterior equivale a (1-y)-n = ∑j≥0 CR(n, j) y j, tal como puede observase en Wikipedia, donde denomina multiset coefficients a las combinaciones con repetición. Con esto tenemos una expresión simplificada para nuestra serie:
| 1 | = ∑n,k≥0 | 1 | xn yk | = ∑n,k≥0 ( ∑j≥0 C(n+j-1, j) y j ) xn yk |
| 1-x-y | (1-y)n |
Volviendo a [7] y sabiendo que 1/(1-x)(1-y) = ∑n,k≥0 xn yk es la serie geométrica con dos variables, tenemos finalmente la serie para G(x, y):
| G(x, y) = | 2xy-x-y+1 | = | 2 | - | 1 | = |
| (1-x)(1-y)(1-x-y) | 1-x-y | (1-x)(1-y) |
Para extraer el término general, hemos de ajustar el rango del sumatorio interior en j=0..k, sucediendo esto:
Podemos ver en Wolframalpha este resultado, con el que llegamos a esa identidad:
| ∑j=0..k C(n+j-1, j) = | k+1 | C(n+k, k+1) = |
| n |
| = | (k+1)(n+k)! | = | (n+k)! | = |
| n (k+1)! (k+n-k-1)! | n k! (n-1)! |
| = | (n+k)! | = C(n+k, k) |
| k! n! |
En el desplegable siguiente puede encontrar una demostración de ese resultado.
así que tenemos
con lo que el término general es el siguiente, comprobándose en la aplicación que el contador de iteraciones coincide con esta expresión:
Nos sirve de confirmación comprobar que se llega al mismo resultado para 1/(1-x-y) en Wikipedia:
| 1 | = ∑n,k≥0 C(n+k, k) xn yk |
| 1-x-y |
Combinaciones con repetición con coste de copia
Ya vimos en un tema anterior sobre el coste total que si el coste sin copia es Ts y la parte de copiar los resultados parciales es Tc = k × R, donde k es la longitud de un resultado y R es el número total de resultados, entonces el coste total será:
Como el número de resultados es:
Entonces
Llegando a esta fórmula final para el coste con copia de resultados:
Esta fórmula coincide con el contador de iteraciones de la aplicación.
Combinaciones con repetición: segunda versión
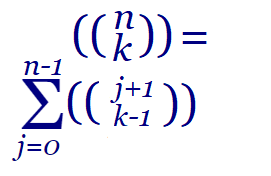
En los apartados anteriores nos basamos en la recurrencia CR(n, k) = CR(n, k-1) + CR(n-1, k) para generar las combinaciones con repetición. Con objeto de encontrar un algoritmo que mejore el coste del anterior, he deducido la identidad que se muestra en la Figura (usando la notación con dos paréntesis para denotar las combinaciones con repetición). Tras hacer los primeros cálculos obtengo una definición de la recurrencia que es exactamente igual a la del tema anterior. Por lo tanto no mejora el coste, pero la exponemos de todas formas.
Este algoritmo se basa en la recurrencia mostrada en la Figura:
Para demostrar esta identidad usaremos la definición CR(n, k) = C(n+k-1, k), desplegando la suma:
Por la identidad del Triángulo de Pascal C(n-1, k-1) = C(n, k) - C(n-1, k) identificaremos cada término de la suma anterior:
Si sumamos todos los términos de la derecha, se observa que los dos primeros resaltados en amarillo se anulan y así sucesivamente, quedando solo los marcados en rojo. El término C(k-1, k) = 0 puesto que cuando a<b ⇒ C(a, b) = 0:
En Wolframalpha puede comprobar que ∑j=0..n-1 C(j+k-1, k-1) = (n/k) C(n+k-1, k-1) = C(n+k-1, k) = CR(n, k).
Este es el algoritmo que implementa la recurrencia. Las instrucciones comentadas no son necesarias para la ejecución. Se descomentan para contar las iteraciones, valor que ha de coincidir con el coste que calculemos en este tema.
// CR(n, k) = ∑j=0..n-1 CR(j+1, k-1)
function combineR2(list=[], k=0, n=list.length, res=Array.from({length:k}, ()=>""), result=[]){
if (k===0 || iter>maxIter){
//iter += 1;
//if (withCopyCost) iter += res.length;
result.push(copy(res));
} else {
//iter += 1;
for (let j=0; j<=n-1; j++){
//iter += 1;
res[k-1] = list[j];
combineR2(list, k-1, j+1, res, result);
}
}
return result;
}Podríamos haber usado la recurrencia siguiente, similar a la anterior:
Se demuestra que es cierta en Wolframalpha con un resultado igual que el anterior: ∑j=0..n C(j+k-2, k-1) = (n/k) C(n+k-1, k-1) = C(n+k-1, k) = CR(n, k). El algoritmo tendría un bucle en el rango j=0 a j<n, teniendo que ajustar la definición de la función con n=list.length-1. En cualquier caso no hay ninguna diferencia en la ejecución, obteniéndose los mismos resultados y coste.
Coste de la segunda versión de combinaciones con repetición
Definimos la recurrencia del algoritmo anterior:
| T(n, k) = { | 1 | if n=0 ∨ k=0 |
| 1 + ∑j=0..n-1 (1 + T(j+1, k-1)) | if n>0 ∧ k>0 |
Partimos de la siguiente definición:
Hemos de evitar el índice negativo k-1, independiente del sumatorio y tratar de evitar este sumatorio. Para ello hacemos lo siguiente:
De donde obtenemos esta expresión:
Esta recurrencia es exactamente igual que la que obtuvimos en el primer apartado, por lo que no es necesario seguir desarrollando. Los resultados obtenidos allí son los mismos que los que obtendríamos aquí. Este para el coste sin copia:
Y este para el coste con copia de resultados:
En la aplicación se comprueba que el contador de iteraciones coincide con estas fórmulas.
Posteriormente a publicar este tema (marzo 2024), detecto que a la hora de definir el coste del algoritmo no tuve en cuenta el coste de montar los argumentos de la llamada inicial que son directamente proporcionales al tamaño del problema. En este algoritmo vemos que tenemos que crear el Array res con k posiciones vacías. Para ello dotaremos de otro argumento start para, en la primera llamada, sumar k al coste total:
// CR(n, k) = ∑j=0..n-1 CR(j+1, k-1)
function combineR2(list=[], k=0, n=list.length, res=Array.from({length:k}, ()=>""), result=[], start=true){
if (start) {
iter += k;
start = false;
}
if (k===0 || iter>maxIter){
iter += 1;
if (withCopyCost) iter += res.length;
result.push(copy(res));
} else {
iter += 1;
for (let j=0; j<=n-1; j++){
iter += 1;
res[k-1] = list[j];
combineR2(list, k-1, j+1, res, result, start);
}
}
return result;
}Por lo tanto sumamos k al coste final sin y con copia: