Calculadora permutaciones cíclicas
Grupo de permutaciones y calculadora de permutaciones cíclicas

Una permutación cíclica es una permutación que fija cero o más elementos y mueve el resto de forma cíclica. Cuando no se fija ningún elemento se denomina permutación circular.
Definimos el Grupo de permutaciones, que denominaremos G, aquel cuyos elementos son permutaciones de un conjunto M. Este conjunto es la lista de elementos con los que hemos venido generando funciones combinatorias en estos temas, algo como M = {1, 2, 3, 4, 5}.
El grupo G dispone de una operación de composición o producto de permutaciones de G que resultan en otra permutación de G, operación que no es conmutativa en general. Como grupo matemático además dispone de un elemento neutro (o pemutación identidad) y de una operación inversa de permutación. La composición o producto no es necesariamente conmutativo, no siendo por ello en general grupos abelianos.
Se denomina acción de grupo a la forma que generamos las permutaciones de M. El grupo simétrico de M es el grupo de todas las permutaciones de M, denotándose como Sim(M) o bien Sn donde n es el número de elementos de M. Obviamente Sn tiene n! elementos, pues hay n! permutaciones en un conjunto con n elementos.
Como ejemplo se suele presentar el Grupo de Klein e isomorfos, por ejemplo sobre el conjunto M = {1, 2, 3, 4}, siendo un subconjunto de S4, con los elementos o permutaciones G = { (), (1 2)(3 4), (1 3)(2 4), (1 4)(2 3) } y con estas características principales:
- Cada elemento es inverso de si mismo, pues la inversa del elemento identidad es el mismo ()-1 = (), y el resto también, como por ejemplo [(1 2)(3 4)]-1 = (1 2)(3 4)
- El producto es, para este grupo, conmutativo, por ejemplo (1 2)(3 4) × (1 3)(2 4) = (1 3)(2 4) × (1 2)(3 4) = (1 4)(2 3), siendo por tanto un grupo abeliano.
- Todas los elementos son pares, por ejemplo signature((1 2)(3 4)) = 1, siendo por esto también un subgrupo del grupo alternante.
Dado que tenemos un grupo con una operación producto, elemento neutro e inversa, implementamos una Calculadora de permutaciones cíclicas en la aplicación Combine Tools, cuyo objeto es poner en práctica los conceptos anteriores.
Como se observa en la Figura, en la calculadora podemos establecer un conjunto M con caracteres cualesquiera, bien números o letras, aunque usualmente suele utilizarse el conjunto numérico M = {1, 2, 3, ..., n}. Disponemos de campos de operandos σ y π que son permutaciones del grupo sobre las que aplicar las siguientes operaciones que expondremos en el resto de apartados de este tema:
- Notación: canonizar, notación 1 y 2 líneas, reglas de permutación
- Convertir númerico ⇆ alfabético
- Es permutación identidad
- Inversiones de una permutación
- Transposiciones de una permutación
- Signo o paridad de una permutación
- Índice de una permutación
- Orden de una permutación
- Desplazamiento σ << 1, σ >> 1
- Son iguales σ == π
- Producto σ × π
- Inversa σ-1
- Potencia σk
- División σ / π
- Matriz de permutación
- Grafo de una permutación cíclica
Notación de permutaciones cíclicas
A veces presentamos una permutación cíclica sin separar los elementos como (1)(243) pues el conjunto de partida no tiene más de 9 elementos. Es lo que denominamos vista de ciclos compactos. Pero en la calculadora de permutaciones cíclicas separamos con un espacio los elementos (1)(2 4 3) para dar posibilidad a conjuntos de cualquier tamaño.
El conjunto de partida suele ser números naturales que empiezan en 1 como M = {1, 2, 3, 4} o letras, como M = {a, b, c, d}. No hay limitación a los elementos, sólo que no podrán haber repetidos, configurándose en orden ascendente. En la aplicación podemos usar elementos con uno o más caracteres cualesquiera a excepción de espacios que se eliminarán y comas, que son necesarias para separar los elementos.
Diferenciamos entre lista numérica con todos los elementos como números enteros correlativos a partir del primer elemento que siempre será 1. Las listas que no cumplan esto se consideran que son alfabéticas, que se ordenan alfabéticamente y no numéricamente.
Por ejemplo, con la lista inicial M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} donde todos los elementos son números enteros desde 1 y son correlativos será una lista numérica. Pero M = {1, 2, 3, 4, 5, 6, 7, 8, 10} donde falta el 9 para ser correlativos, se reordenará como M = {1, 10, 2, 3, 4, 5, 6, 7, 8} y se considera una lista alfabética, donde alfabéticamente "10" se ordena antes de "2". Igualmente, si están correlativos pero no empieza en 1 también será alfabética como M = {4, 5, 6, 7, 8, 9, 10, 11, 12} ordenándose con M = {10, 11, 12, 4, 5, 6, 7, 8, 9}.
El conjunto de números romanos M = {I, II, III, IV, V, VI, VII, VIII} es una lista alfabética pues sus elementos no son números enteros. Vea que si agregamos "IX" que es el siguiente número romano 9, se ordenará M = {I, II, III, IV, IX, V, VI, VII, VIII} después de IV y no al final.
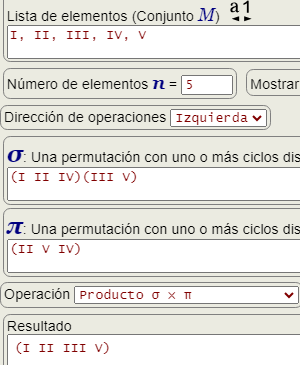
En la Figura puede ver M1 = {I, II, III, IV, V} con el producto de permutaciones cíclicas (I II IV)(III V) * (II V IV) = (I II III V) obteniéndose lo mismo que vemos en la Figura 1 con M2 = {1, 2, 3, 4, 5} y el producto (1 2 4)(3 5) * (2 5 4) = (1 2 3 5). Se obtiene lo mismo pues hay una correspondencia entre M1 y M2, pues el orden se conserva en ambos hasta n=8.
El orden de los elementos es importante, pues en algunas operaciones se deben ordenar los elementos en los ciclos, teniendo que diferenciar entre listas numéricas y alfabéticas. Es más fácil trabajar con el conjunto M = {1, 2, 3, 4, ..., n}, pero doy la posibilidad de utilizar elementos que son palabras sin espacios de uno o más caracteres, con objeto de unificar la lista de elementos con las que usamos en la aplicación para generar listas combinatorias.
La relación entre las permutaciones normales y su representación cíclica se puede observar en esta tabla para el conjunto M = {1, 2, 3} que genera 3! = 6 permutaciones permute(1 2 3) = {1 2 3, 1 3 2, 2 1 3, 2 3 1, 3 1 2, 3 2 1}
| Notación 1 línea | Notación cíclica | Notación cíclica canonizada | Fija |
|---|---|---|---|
| 1 2 3 | (1)(2)(3) | () | Todos |
| 1 3 2 | (1)(2 3) | (2 3) | 1 |
| 2 1 3 | (1 2)(3) | (1 2) | 3 |
| 2 3 1 | (1 2 3) | (1 2 3) | Ninguno |
| 3 1 2 | (1 3 2) | (1 3 2) | Ninguno |
| 3 2 1 | (1 3)(2) | (1 3) | 2 |
Podemos entender el conjunto M como un array donde cada elemento está en una posición determinada. Podríamos usar el siguiente esquema para representar la correspondencia entre la posición i y su valor σ(i), siendo σ una permutación del conjunto M, donde la primera línea indica la posición en el array (empezando en 1) y la segunda el valor del elemento que contiene, disposición que denominamos notación en dos líneas:
i 1 2 3 4 σ(i) a b c d
Usualmente solemos verlo como una matriz con dos líneas:
| ⎧ | 1 | 2 | 3 | 4 | ⎫ |
| ⎩ | a | b | c | d | ⎭ |
Como la primera línea siempre es una lista númerica que empieza en 1 en orden ascendente, es suficiente utilizar a b c d para identificarlo, lo que se conoce como notación en una línea. Esta aplicación σ = a b c d = ε es la permutación identidad, que hace corresponder los valores de M en su orden inicial y que se suele identificar con la letra "e" de elemento neutro, pero que aquí denotaremos con "ε" para no confundirlo con un elemento de M.
Si desordenamos la segunda fila de valores, por ejemplo tendremos esta otra permutación σ = a d b c:
i 1 2 3 4 σ(i) a d b c
Para aclararnos incluimos un subíndice en cada σ(i) indicando el índice que ocupa en el conjunto M = {a, b, c, d}
i 1 2 3 4 σ(i) a1 d4 b2 c3
que podemos presentar así:
σ(1) = a1 σ(2) = d4 σ(3) = b2 σ(4) = c3
Como σ(1) = a1 coincide el 1 en el argumento de la izquierda con en el subíndice de la derecha, tenemos un ciclo unitario (a). Para rel resto los ordenamos de tal forma que en primer lugar ponemos el menor subíndice i en la derecha, que resulta ser σ(3) = b2 y a continuación buscamos el mismo índice σ(i) en la izquierda sucesivamente hasta que veamos que volvemos al primero:
σ(3) = b2 σ(2) = d4 σ(4) = c3
Estos tres conforman la cadena σ(3) = b2 → σ(2) = d4 → σ(4) = c3, que es lo mismo que decir b → d → c observando que el último apunta al primero cerrando el ciclo, con lo que lo denotamos como (b d c).
Finalmente tenemos σ = (a)(b d c) en notación de ciclos que se corresponde con σ = a d b c en notación de una línea. En la aplicación puede encontrar la operación Notación línea a ciclos que obtiene la notación en ciclos a partir de una notación en línea.
Es más fácil visualizar todo esto si el conjunto es numérico, usando M = {1, 2, 3, 4} en lugar de M = {a, b, c, d}. Veamos la misma permutación de antes σ = a d b c que en este conjunto numérico es σ = 1 4 2 3:
i 1 2 3 4 σ(i) 1 4 2 3
Ahora es más fácil seguir la cadena con 1 → 1, 2 → 4, 4 → 3, 3 → 2 y deduciéndose la permutación cíclica (1)(2 4 3) que se corresponde con 1 4 2 3 en notación de una línea. En el fondo es la misma que (a)(b d c) basándonos en la correspondencia entre ambos conjuntos {1, 2, 3, 4} y {a, b, c, d}
Para pasar de notación cíclica a notación en dos líneas sólo tenemos que fijar la secuencia (1)(2 4 3) ⇒ 1 → 1, 2 → 4, 4 → 3, 3 → 2 observando que en cada ciclo un elemento apunta a si mismo si es ciclo unitario o al siguiente o al primero si el el último del ciclo. Con esa cadena de correspondencias es fácil componer la notación en dos líneas obteniéndose 1 4 2 3:
i 1 2 3 4 σ(i) 1 4 2 3
Fijando el primer elemento y con los tres elementos restantes las únicas posibilidades de permutaciones cíclicas diferentes son estas dos:
(1)(2 4 3) = (1)(3 2 4) = (1)(4 3 2)
El orden dentro de cada ciclo si es importante pues puede ser de uno u otro grupo. Pero el orden de los ciclos no es importante pues los ciclos son disjuntos, siendo equivalente disponer el ciclo unitario al principio o al final:
(1)(2 4 3) = (1)(3 2 4) = (1)(4 3 2) = (2 4 3)(1) = (3 2 4)(1) = (4 3 2)(1)
La forma canónica se basa en usar en cada ciclo el equivalente que tenga el primer menor elemento y ordenar los ciclos por su primer elemento, con lo cual es importante diferenciar entre listas numéricas y alfabéticas. Así todos los de la segunda línea anterior se canonizan como (1)(2 4 3). Sin embargo Wolfram Alpha canoniza (1)(3 2 4) como (2 4 3)(1) poniendo en color gris los ciclos unitarios al final. Pero eso es indiferente, pues tanto (1)(2 4 3) como (2 4 3)(1) conducen a la misma permutación 1 4 2 3.
La regla de permutación de (1)(2 3 4) es 1→1 | 2→3 | 3→4 | 4→2 se obtiene iterando por lo valores 1, 2, 3, 4 y buscando el siguiente elemento en cada ciclo, bien a sí mismo en caso de ciclos unitarios, o en caso del último del ciclo apuntaría al primero en el mismo ciclo. Observe que para las dos equivalentes (1)(4 2 3) y (1)(3 4 2) se obtiene la misma regla. Pero no así para el otro grupo cuya canónica es (1)(2 4 3) y cuya regla es 1→1 | 2→4 | 3→2 | 4→3, que también se obtiene con sus equivalentes (1)(3 2 4) y (1)(4 3 2).
Como notación alternativa, conviene indicar que en una permutación cíclica como esa (1)(2 3 4) es posible no incluir los ciclos unitarios y poner simplemente (2 3 4), de tal forma que los elementos faltantes del conjunto {1, 2, 3, 4} se entienden que son ciclos unitarios. Sin embargo si se usa esta alternativa siempre hay que indicar el conjunto, pues si en este ejemplo el conjunto tiene más de 4 elementos, todos los que falten serán ciclos unitarios.
Observe que la permutación identidad ε = 1 2 3 4 en notación de una línea se denota como (1)(2)(3)(4) en notación cíclica. Cada ciclo unitario es un punto fijo de la permutación. A veces se ocultan los puntos fijos, por lo que (1)(2 3 4) se presenta como (2 3 4). Y se suele presentar la identidad como ε = (1) o simplemente ε = ().
Convertir númerico a alfabético y viceversa (numericAlphabetic)
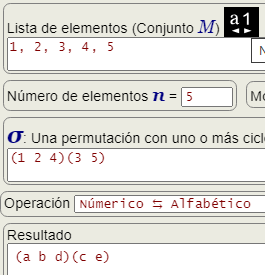
El botón es una utilidad de la aplicación para cambiar una lista numérica como M = {1, 2, 3, 4} en una alfabética M = {a, b, c, d} y al revés.
La operación Númerico ⇆ Alfabético realiza esa conversión en la permutación cíclica, como en el ejemplo de la Figura que convierte, la permutación (1 2 4)(3 5) en (a b d)(c e).
La conversión se realiza con el primer caracter de cada elemento. Está pensado para conjuntos numéricos M = {1, 2, 3, ...} de tal forma que se hacen corresponder con los caracteres a, b, c, ... siguiendo el orden que tienen en UNICODE iniciándose en la letra "a".
Permutaciones cíclicas en Wolfram Alpha
El enlace con el icono pemite abrir la página web de Wolfram Alpha para evaluar la operación. Sólo estará activo con listas numéricas, que son como M = {1, 2, 3, ..., n} como explicamos en el apartado anterior, pues esa página no reconoce otras listas. Y con aquellas operaciones que esa página tiene en cuenta.
Por ejemplo, la operación inversa inverse (1 2 4)(3 5) = (1 4 2)(3 5) conforma el enlace inverse (1 2 4)(3 5) para Wolfram Alpha, obteniéndose el mismo resultado. Ese recurso es muy útil pues da mucha información sobre la permutación, cuya mayor parte he tenido en cuenta para aplicarlo a la calculadora de permutaciones cíclicas.
Es identidad una permutación cíclica (isIdentity)
Una permutación cíclica es la identidad si todos sus ciclos son unitarios. Si el conjunto es {1, 2, 3, 4} entonces la permutación identidad es (1)(2)(3)(4), que si ocultamos los ciclos unitarios se representa con (). La operación isIdentity σ nos devuelve si σ es o no es una permutación identidad.
No encuentro una forma de expresar esto en Wolfram Alpha.
Inversiones de una permutación cíclica (inversions)
Si σ es una permutación cíclica hay una inversión entre los índices i y j si i<j y σ(i)>σ(j). La inversión puede representarse como la pareja [i, j] basada en índices o bien como [σ(i), σ(j)] basada en elementos, que es la que usamos en la aplicación. La función Inversiones (B) utiliza el basado en índices, que es el que podemos ver en la página de Wolfram Alpha (usando el botón "Show list").
Por ejemplo, con la operación inversions (1 2 4)(3 5) otenemos las parejas de elementos [[2, 1], [4, 1], [4, 3], [5, 1], [5, 3]]. En cambios si usamos la operación inversionsB (1 2 4)(3 5) obtenemos las parejas de índices [[1, 4], [2, 4], [2, 5], [3, 4], [3, 5]], que es la misma que la que podemos ver en Wolfram Alpha, tras utilizar el botón "Show list" (Mostrar lista), pues inicialmente lo presenta como un grafo de inversión que no ejecutamos en la aplicación.
Presentando σ = (1 2 4)(3 5) en notación de dos líneas
i 1 2 3 4 5 σ(i) 2 4 5 1 3
podemos ver como es el proceso para obtener las inversiones:
- Vemos que de las parejas de índices [1, j] con j>1 sólo la pareja [1, 4] cumple que σ(1) > σ(4) ⇒ 2 > 1.
- A continuación vemos las parejas de índices [2, j] con j>2, donde para las parejas de índices [2, 4], [2, 5] se cumple que σ(2) > σ(4) ⇒ 4 > 1 y σ(2) > σ(5) ⇒ 4 > 3.
- Seguimos con este proceso a la derecha observando las parejas [3, j] con j>3, encontrando [3, 4], [3, 5] en índices que hacen mayores que los anteriores los valores [5, 1], [5, 3].
- La últimas parejas a observar son las del tipo [4, j] con j>4 donde no hay ninguna pues la única posibilidad con índices [4, 5] tiene valores menores [1, 3].
Transposiciones de una permutación cíclica (transpositions)
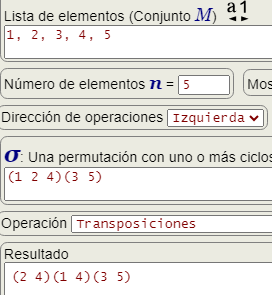
Una transposición es una permutación que intercambia dos elementos fijando el resto, lo que supone que es una permutación con un ciclo de longitud 2 y el resto de longitud 1 o puntos fijos. Cualquier permutación se puede construir como una composición (o producto) de transposiciones de muchas formas, pero en cualquier caso con un número de ellas que siempre será el mismo. Este número sirve para identificar la signatura como veremos en el siguiente apartado.
Sea transpositions (1 2 4)(3 5) = (1 4)(2 4)(3 5) con dirección de operaciones derecha. El resultado no es una permutación cíclica, pues sus ciclos no son disjuntos. Pero como explicamos en el apartado composición o producto, una permutación con ciclos siempre puede entenderse como un producto de ciclos, dado que el producto de dos ciclos disjuntos no modifica el resultado. Por ejemplo (2 4) × (3 5) = (2 4)(3 5), con lo que en la permutación cíclica (2 4)(3 5) podemos entender la operación × producto implícita entre los paréntesis de ciclos disjuntos. Así que las transposiciones debe entenderse como un producto de ciclos de longitud dos: (1 4)×(2 4)×(3 5), recordando que al no ser conmutativo el producto, el orden de los ciclos si importa así como la dirección de operaciones (derecha en este ejemplo) que se explica en el apartado producto.
Observe que la forma de extraer las transposiciones es observar que el ciclo (3, 5) se deja como está pues ya tiene longitud 2. En otro caso para (1, 2, 4) tomamos como pivote el último 4 y componemos ciclos de longitud 2 con el resto (1 4)(2 4). Esta forma es la que usa también Wofram Alpha con transpositions (1 2 4)(3 5). Hay que tener en cuenta que Wolfram Alpha usa la composición derecha, pues como explicamos en el apartado del composición o producto de dos permutaciones cíclicas hay dos posibles direcciones de operaciones derecha e izquierda, pues el producto no es conmutativo en general.
En composición izquierda tenemos transpositions (1 2 4)(3 5) = (2 4)(1 4)(3 5) tal como se observa en la Figura. Observamos que se trata de invertir el orden (1 4)(2 4) por (2 4)(1 4), dejando como está (3 5) pues ya era un ciclo de longitud 2 en la permutación inicial.
Aplicando la propiedad asociativa a ambas transposiciones con composición derecha e izquierda respectivamente para cada transposición anterior, observamos que llegamos a la permutación inicial (1 2 4)(3 5):
- Derecha:(1 4)(2 4)(3 5) = [(1 4) × (2 4)] × (3 5) = (1 2 4) × (3 5) = (1 2 4)(3 5)
- Izquierda:(2 4)(1 4)(3 5) = [(2 4) × (1 4)] × (3 5) = (1 2 4) × (3 5) = (1 2 4)(3 5)
Pero como hemos dicho, esta no es la única forma de obtener transposiciones, pudiendo relacionar las siguientes siendo un ciclo como (a1 a2 ··· ak) donde cada ai es un elemento cualquiera del conjunto M = {1, 2, 3, ..., n} con operaciones en dirección izquierda:
- que es la que hemos usado en el ejemplo de los párrafos anteriores y en la aplicación. Ejemplo transpositions (1 2 3 4) = (3 4)(2 4)(1 4)transpositions (a1 ··· ak) = (ak-1 ak)(ak-2 ak)···(a2 ak)(a1 ak)
- Ejemplo transpositions (1 2 3 4) = (1 4)(1 3)(1 2)transpositions (a1 ··· ak) = (a1 ak)(a1 ak-1)···(a1 a3)(a1 a2)
- Ejemplo transpositions (1 2 3 4) = (1 2)(2 3)(3 4)transpositions (a1 ··· ak) = (a1 a2)(a2 a3)···(ak-2 ak-1)(ak-1 ak)
Para usar dirección derecha sólo hay que invertir el orden de los ciclos, quedando los ejemplos anteriores con (1 4)(2 4)(3 4) para el primer ejemplo, (1 2)(1 3)(1 4) para el segundo y (3 4)(2 3)(1 2) para el tercero.
Observe que sea cual sea la forma de obtener las transposiciones, siempre obtendremos el mismo número de ciclos, 3 en el caso de transpositions (1 2 3 4), obteniéndose ese mismo número independientemente de la dirección de operaciones.
Signatura, signo o paridad de una permutación cíclica (signature)
Se dice que una permutación σ es par si σ se descompone en un número par de ciclos de transposiciones o incluye un número par de inversiones. Y lo mismo para impar. El signo o signatura será +1 si es par y -1 si es impar.
Si obtenemos las inversiones de (1 2 4)(3 5) veremos que son 5 y por tanto es impar y así que tiene signo negativo:
impar ⇒ signo = (-1)5 = -1
Y con transposiciones llegamos al mismo signo:
impar ⇒ signo = (-1)3 = -1
En la aplicación tenemos las operaciones signature (1 2 4)(3 5) = -1 que usa inversiones y signatureB (1 2 4)(3 5) = -1 que usa transposiciones, obteniéndose el mismo resultado -1 (impar). En ambos casos es independiente de la dirección de operaciones, como podemos comprobar en Wolfram Alpha signature of permutation (1 2 4)(3 5) que usa composición derecha.
Índice de una permutación cíclica (index)
El índice de una permutación σ es la suma de todos los índices tal que σ(i) > σ(i+1), que podemos expresar como index σ = Σi | σ(i) > σ(i+1) i
Con la permutación σ = (1 2 4)(3 5) en notación de 2 líneas
i 1 2 3 4 5 σ(i) 2 4 5 1 3
vemos que la suma de los casos donde σ(i) > σ(i+1) resulta que index (1 2 4)(3 5) = 3
σ(1) > σ(2) ⇒ 2 > 4 ⇒ +0 σ(2) > σ(3) ⇒ 4 > 5 ⇒ +0 σ(3) > σ(4) ⇒ 5 > 1 ⇒ +3 σ(4) > σ(5) ⇒ 1 > 2 ⇒ +0
En Wolfram Alpha podemos obtenerlo con index of (1 2 4)(3 5).
Orden de una permutación cíclica (order)
El órden de una permutación es la potencia positiva más baja con la que se obtiene la permutación identidad. Para ver esto hemos de usar la operación potencia de una permutación σ, que podemos escribir como σk.
Sea σ = (1 2 4)(3 5). En la aplicación obtenemos orden σ = 6. Obtengamos las primeras potencias positivas:
σ1 = (1 2 4)(3 5)
σ2 = (1 4 2)
σ3 = (3 5)
σ4 = (1 2 4)
σ5 = (1 4 2)(3 5)
σ6 = ()
σ7 = (1 2 4)(3 5)
Se observa que con k=6 volvemos a obtener la permutación identidad (), siendo entonces de orden 6. A partir de ahí vuelven a repetirse los resultados anteriores.
Desplazamiento de una permutación cíclica (shift)
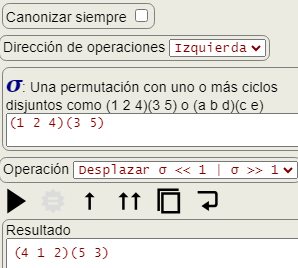
La operación desplazamiento de una permutación consiste en desplazar los elementos a la derecha o izquierda de forma cíclica. Tal como se observa en la Figura, se realiza según el control dirección de operaciones a la derecha o a la izquierda. Además la opción canonizar siempre debe estar desmarcado, pues el canonizado consiste en usar el ciclo con el menor elemento al inicio, que se llevará a cabo con cada ejecución si la opción está marcada.
Desplazar (1 2 4)(3 5) a la izquierda resultará en (4 1 2)(5 3).
Comparar igualdad de dos permutaciones cíclicas (isEqual)
Con las permutaciones σ = (1 2 4 7)(3 6 5)(8 9) y π1 = (2 4 7 1)(3 6 5)(9 8) sucede que σ == π1, pero con π2 =(7 2 1 4)(3 6 5)(8 9) resulta que σ ≠ π2 pues no son iguales. Esta operación isEqual se basa en desplazar los ciclos de alguna de ellas hasta comprobar que ambas sean iguales.
Otra operación es isEqual (B) que realiza la operación isIdentity(σ ÷ π) usando las operaciones División y Es identidad.
Producto de dos permutaciones cíclicas (product)
El producto o composición de permutaciones es la operación que, junto a la existencia de la permutación identidad y de la inversa de una permutación, caracteriza el Grupo de permutaciones cíclicas. Si σ y π son dos permutaciones del grupo G, entonces el producto σ × π también pertenece a G.
Veamos el ejemplo σ = (1 2 4)(3 5) y π = (1 3 4), ambas presentadas de forma canónica, obteniéndose el producto σ × π = (1 2 4)(3 5) × (1 3 4) = (1 5 3)(2 4). Veamos paso a paso como llevar a cabo el producto.
La dirección de operaciones para este ejemplo es izquierda, pues recordemos que si se usa la contraria se obtiene otro resultado. En primer lugar completamos las permutaciones con los puntos fijos:
Como la dirección de operaciones es izquierda, se trata de seguir la cadena de enlaces desde la permutación de la derecha hasta la permutación de la izquierda. Buscamos ese pivote 1 en la permutación π de la derecha, viendo que el siguiente es 3, que lo buscamos en la permutación σ de la izquierda y vemos que apunta a 5:
Como 5 no está en el nuevo ciclo, lo agregamos:
Cambiando el pivote al último encontrado pivot = 5, lo buscamos en la derecha viendo que apunta a sí mismo por ser un punto fijo, buscamos 5 en la izquierda y vemos que apunta a 3, que al no estar en el nuevo ciclo lo agregamos (1 5 3...:
Ahora tenemos pivot = 3, que en la derecha apunta a 4, que lo buscamos en la izquierda y apunta a 1 (pues el último apunta al primero), que al ya estar 1 en el nuevo ciclo (1 5 3... cerramos este ciclo:
Al cerrar un ciclo actualizamos M = {2, 4} quitando los elementos que ya hemos incluido en el ciclo que acabamos de cerrar. Iniciamos un nuevo ciclo tomando el primero pivot = 2 e iniciando un nuevo ciclo (2 ... Buscamos 2 en la derecha, que apunta a sí mismo, buscamos en la izquierda y vemos que apunta a 4, que al no estar en el nuevo ciclo, lo agregamos:
Buscamos 4 en la derecha, apunta a 1, que buscándolo en la izquieda apunta a 2, que al estar ya en el nuevo ciclo, lo cerramos:
Actualizando M = {} con los elementos ya incluidos en los nuevos ciclos, vemos que ya no tenemos más elementos y, por tanto, hemos finalizado el producto con el resultado esperado σ × π = (1 2 4)(3 5) × (1 3 4) = (1 5 3)(2 4)
Como hemos dicho, la dirección de operaciones es importante, pues no se obtiene el mismo resultado. Con dirección derecha σ × π = (1 2 4)(3 5) × (1 3 4) = (1 2)(3 5 4). Esta forma es la que usa Wolfram Alpha permutation (1 2 4)(3 5) * (1 3 4)
Vease que el producto no es conmutativo, así que si ×left es el producto con dirección izquierda y ×right es con dirección derecha, sucede que:
y de igual forma:
La dirección izquierda suele ser preferente pues se asimila a la composición de funciones, donde (g ∘ f)(x) = g(f(x)). De forma equivalente σ × π = σ(π(i)) en dirección izquierda, donde primero se procesa en π a la derecha buscando luego en σ a la izquierda. Por eso la dirección es izquierda. Wolfram Alpha usa σ × π = π(σ(i)) en dirección derecha. Como acabamos de ver, para unificar resultados con distinta dirección, solo tenemos que intercambiar los operandos.
El producto de ciclos disjuntos no modifica la permutación. Por ejemplo, si σ = (1 2 4) y π = (3 5), vemos que son disjuntos pues no comparten elementos, entonces σ × π = (1 2 4) × (3 5) = (1 2 4)(3 5). En una permutación cíclica como (1 2 4)(3 5), donde los ciclos son disjuntos, puede incluirse un producto entre los ciclos (1 2 4)×(3 5) sin que ello modifique la permutación.
Esto es lo que vimos en el apartado de transposiciones, donde usábamos la propiedad asociativa de tal forma que para el producto de tres permutaciones podemos hacer:
Por ejemplo, usando dirección izquierda, podemos agrupar los dos primeros:
= ( (1 2 4)(3 5) × (1 3 4) ) × (1 4)(2 5 3) =
= (1 5 3)(2 4) × (1 4)(2 5 3) = (1 2 3 4 5)
o bien los dos últimos, obteniéndose en ambos casos el mismo resultado:
= (1 2 4)(3 5) × ( (1 3 4) × (1 4)(2 5 3) ) =
= (1 2 4)(3 5) × (2 5 4 3) = (1 2 3 4 5)
Obviamente si ε = () es la permutación identidad, entonces σ × ε = ε × σ = σ donde el producto resulta en la misma permutación. Vea que aunque σ × π ≠ π × σ pues el producto no es conmutativo en general, a excepción de cuando un operando es la permutación identidad.
Inversa de una permutación cíclica (inverse)
Un grupo de permutaciones se caracteriza por la composición o producto, permutación identidad y existencia de inversa de una permutación. Si σ es una permutación y σ-1 es su inversa entonces la composición o producto de ambas resulta en la permutación identidad: ε = σ × σ-1
Por ejemplo, la inversa de σ = (1 2 4)(3 5) es σ-1 = (1 4 2)(3 5). Y su producto es σ × σ-1 = (1 2 4)(3 5) × (1 4 2)(3 5) = () la permutación identidad.
Para obtener la inversa sólo tenemos que invertir los ciclos y también los elementos dentro de cada ciclo. Así, antes de canonizar, (1 2 4)(3 5) ⇒ (5 3)(4 2 1) que después de canonizar queda (1 4 2)(3 5).
En Wolfram Alpha se obtiene con inverse (1 2 4)(3 5)
Potencia de una permutación cíclica (power)
La potencia a un exponente k positivo de una permutación es simplemente aplicar la composición o producto k veces. Por ejemplo, si σ = (1 2 4)(3 5) y k=3 entonces σ3 = (3 5)
Si k=1 resulta σ1 = σ la misma permutación, lo cual es obvio. Si k=0 entonces σ0 = ε resulta la permutación identidad, lo que parece menos obvio.
Si el exponente es negativo entonces como σ-k = (σ-1)k con lo que aplicamos la potencia positiva a la inversa de la permutación. Por ejemplo:
= ( ( (1 2 4)(3 5) )-1 )3 =
= ( (1 4 2)(3 5) )3 =
= (3 5)
Wolfram Alpha obtiene ese resultado con permutation (1 2 4)^-3 (3 5)^-3, que resulta en aplicar el exponente a cada ciclo y considerar que hay implícito un producto entre los ciclos, resolviendo la potencia de cada ciclo y luego aplicando la propiedad asociativa para resolver los prouctos si hay más de dos operandos, como en el siguiente ejemplo:
= (1 3 7)2 (2 8 4 5)2 (6 9)2 =
= (1 3 7)2 × (2 8 4 5)2 × (6 9)2 =
= (1 7 3) × (2 4)(5 8) × () =
= ((1 7 3) × (2 4)(5 8) ) × () =
= (1 7 3)(2 4)(5 8) × () =
= (1 7 3)(2 4)(5 8)
Puede ver en permutation (1 3 7)^2 (2 8 4 5)^2 (6 9)^2 el resultado en Wolfram Alpha.
División de dos permutaciones cíclicas (division)
La división σ ÷ π entre dos permutaciones cíclicas no es más que aplicar el producto o composición σ × π-1 entre la primera permutación y la inversa de la segunda.
Por ejemplo, (1 2 4)(3 5) ÷ (1 3 4) = (2 4 5 3) que es lo mismo que aplicar el producto (1 2 4)(3 5) × (1 3 4)-1 = (1 2 4)(3 5) × (1 4 3) = (2 4 5 3)
Una forma de saber si dos permutaciones son iguales es usando la división, pues σ = π ⇔ σ ÷ π = ε resultando en la permutación identidad. Esto es lo que usamos para implementar la operación Es igual (B).
Matriz de una permutación cíclica (matrix)
La matriz de una permutación cíclica σ de un conjunto M = {1, 2, 3, ..., n} es cuadrada con i = 1..n filas y j = 1..n columnas. Una posición (i, j) = 1 si σ(i) → σ(j), es decir, σ(i) antecede a σ(j). En otro caso la posición es cero.
Por ejemplo, la matriz de (1 2 4)(3 5) tiene esta forma:
| ⎧ | 0 | 1 | 0 | 0 | 0 | ⎫ |
| ⎪ | 0 | 0 | 0 | 1 | 0 | ⎪ |
| ⎪ | 0 | 0 | 0 | 0 | 1 | ⎪ |
| ⎪ | 1 | 0 | 0 | 0 | 0 | ⎪ |
| ⎩ | 0 | 0 | 1 | 0 | 0 | ⎭ |
En Wolfram Alpha podemos obtenerla con matrix of permutation (1 2 4)(3 5).
Una forma práctica de obtenerla es tomando la notación en una línea, que para el ejemplo (1 2 4)(3 5) es 2 4 5 1 3, disponiendo los elementos de M = {1, 2, 3, 4, 5} en una fila (resaltados en amarillo) y la permutación 2 4 5 1 3 en una primera columna. Luego buscamos la columna donde se ubica cada σ(i) en M
i 1 2 3 4 5 2 - 2 - - - 4 - - - 4 - 5 - - - - 5 1 1 - - - - 3 - - 3 - -
Cambiando los guiones por ceros y los números por unos, obtenemos la matriz anterior. En la aplicación obtenemos el resultado como un Array:
[[0,1,0,0,0], [0,0,0,1,0], [0,0,0,0,1], [1,0,0,0,0], [0,0,1,0,0]]
Grafo de una permutación cíclica (graph)
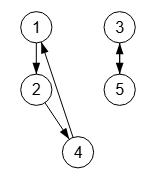
(1 2 4)(3 5)
El grafo de una permutación cíclica nos da una representación visual de los ciclos, facilitando la observación de la cadena de enlaces entre los valores. Existirán tantos subárboles como ciclos, siendo todos los subárboles cíclicos. Cada nodo representa un elemento, con una flecha que apunta al siguiente elemento en el ciclo.
Para el ejemplo (1 2 4)(3 5) es el que vemos en la Figura. Con Wolfram Alpha podemos obtenerlo con cycle graph of permutation (1 2 4)(3 5).
Usamos el editor de grafos de Web Tools online que necesita un objeto con los valores y la configuración. Nuestra aplicación obtiene el siguiente para el ejemplo (1 2 4)(3 5):
{"nodes":[
{"index":0,"value":1,"parent":[{"index":-1},{"index":3,"lineComment":"4→1"}]},
{"index":1,"value":2,"parent":[{"index":0,"lineComment":"1→2"}]},
{"index":3,"value":4,"parent":[{"index":1,"lineComment":"2→4"}]},
{"index":2,"value":3,"parent":[{"index":-1},{"index":4,"lineComment":"5→3"}]},
{"index":4,"value":5,"parent":[{"index":2,"lineComment":"3→5"}]}
],
"config":{
"markerStart":"arrow",
"markerEnd":"none"
}
}Esta estructura es un JSON y se explica en el tema Web Tools online: Grafos con SVG.
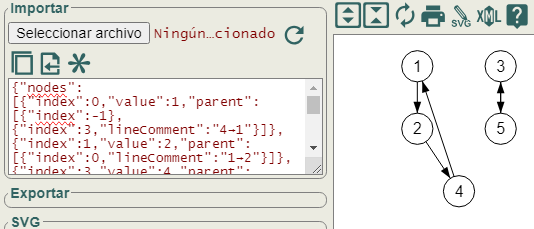
Como se observa en la Figura, es posible copiar el texto o bien desde un archivo exterior para importar el grafo.
Cada entrada del Array "nodes" es un nodo del grafo. Y "parent" es un Array con los ascendentes o padres. El primer nodo de cada subárbol apunta a -1. Y luego puede apuntar a otro nodo. Por ejemplo, el primero con index = 0 es el nodo 1 (value = 1), cuyo padre es el 4, con index = 3 (value = 4). El campo "lineComment":"4→1" son comentarios que no se visualizan de las aristas o líneas entre dos nodos, en este caso 4→1, que nos sirve para encontrar cada componente de la permutación en el Array "nodes".
En la configuración config hay que agregar "markerStart": "arrow", "markerEnd": "none" pues el comportamiento por defecto es al revés.
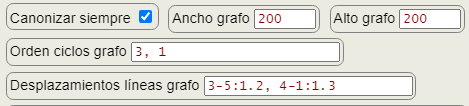
En la aplicación Combine Tools podemos configurar algunos parámetros antes de ejecutar el grafo, como vemos en la Figura. Hemos reducido el ancho y alto a 200 × 200 píxeles. Incluímos en orden ciclos grafo la lista 3, 1 para que salga primer el subárbol con raíz 3 y luego el 1. Ese campo permite poner asc para orden ascendente, desc para descendente o una lista de nodos raíz con el orden que se precise. Si no se incluye nada se usa el orden de la permutación.
Otro parámetro que podemos configurar es el de desplazamiento líneas del grafo, donde hemos configurado 3-5:1.2, 4-1:1.2. Esto significa que la línea que une 3→5 será desplazada 1.2 unidades a la derecha (si es negativo se desplaza a la izquierda). Y que la línea que une 4→1 será desplazada 1.3 unidades también a la derecha. Con estos parámetros el grafo queda como vemos en Figura.
Este grafo de la Figura 9 es un SVG, mientra que el de la Figura 6 es un PNG. La aplicación permite descargarlo en varios formatos, como se observa en la Figura.
El JSON resultante con esos cambios es el siguiente, donde se observa que "lineOffset" implementa el desplazamiento de las líneas afectadas.
{"nodes":[{"index":2,"value":3,"parent":[{"index":-1},{"index":4,"lineComment":"5→3"}]},
{"index":4,"value":5,"parent":[{"index":2,"lineComment":"3→5","lineOffset":1.2}]},
{"index":0,"value":1,"parent":[{"index":-1},{"index":3,"lineComment":"4→1","lineOffset":1.3}]},
{"index":1,"value":2,"parent":[{"index":0,"lineComment":"1→2"}]},
{"index":3,"value":4,"parent":[{"index":1,"lineComment":"2→4"}]}],
"config":{"markerStart":"arrow","markerEnd":"none","width":200,"wv":80,"height":200,"hv":80}}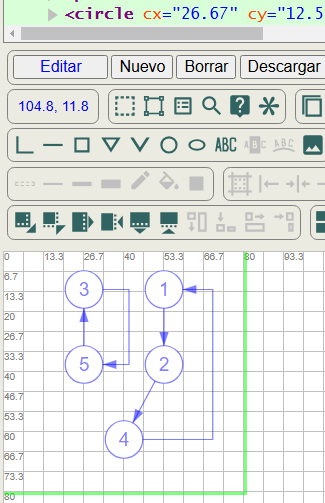
Por último indicar que podemos editar el SVG con la herramienta Web Tools online, como se observa en la Figura.