Operaciones básicas en un grafo
Operaciones en grafos
En la aplicación Grafos SVG podemos acceder al asistente de generación mediante el botón . El desplegable de la acción tiene dos partes: una primera con las operaciones que podemos ejecutar sobre un grafo que veremos en este tema y otra segunda para generar nuevos grafos que se expondrá en otro tema.
Las operaciones en grafos producen nuevos grafos diferentes de los iniciales. Se ejecutan sobre la matriz de adyacencia modificándola y, por tanto, modificando también el grafo.
Una clasificación de las operaciones en grafos es la siguiente:
- Operaciones unarias sobre un único grafo:
- Operaciones básicas o de edición son las que modifican el grafo con acciones como agregar o eliminar nodos o aristas, contracción, división y subdivisión. Esto lo explicamos en el tema edición de nodos y aristas cuando esas operaciones se ejecutan desde la estructura JSON, lo que se lleva a cabo con los botones Pero también podemos ejecutar esas mismas operaciones sobre la matriz de adyacencia, que son las operaciones que exponemos en este tema:
- Edición grafo
operateEditionGraph() - Contracción grafo
operateContractionGraph() - División grafo
operateSplittingGraph() - Subdivisión grafo
operateSubdivisionGraph
- Edición grafo
- Operaciones avanzadas crean un nuevo grafo con un cambio más complejo que veremos en el siguiente tema:
- Cambiar dirección con
operateDirectionGraph(), que ya vimos en el tema anterior, cambiando la dirección de toda las aristas siguiendo un criterio particular de la aplicación. - Grafo complemento con
operateComplementGraph() - Grafo transpuesto con
operateTransposeGraph()que ya vimos en el tema anterior, transponiendo la matriz de adyacencia. - Grafo línea con
operateLineGraph() - Permutar un grafo con
operatePermuteGraph() - Grafo cociente con
operateQuotientGraph()
- Cambiar dirección con
- Operaciones básicas o de edición son las que modifican el grafo con acciones como agregar o eliminar nodos o aristas, contracción, división y subdivisión. Esto lo explicamos en el tema edición de nodos y aristas cuando esas operaciones se ejecutan desde la estructura JSON, lo que se lleva a cabo con los botones Pero también podemos ejecutar esas mismas operaciones sobre la matriz de adyacencia, que son las operaciones que exponemos en este tema:
- Operaciones binarias que involucran dos grafos, como principalmente la unión, la intersección y el producto de dos grafos que tampoco he implementado.
El asistente de generación, al que se accede mediante el botón , se muestra en la Figura. Ahí podemos ejecutar las operaciones.
Tras la ejecución ofrece el resultado como un objeto con el posible mensaje de error y la matriz de adyacencia resultante. El botón "Restablecer" permite deshacer la acción y volver al grafo original. La opción "Posicionar" fija la posición original de los nodos.
El icono es un vínculo que nos lleva a una página de información en este sitio, explicando los detalles de la operación. El botón abre un panel con el código JavaScript de la operación.
En la parte de "Código Wolfram" se ofrece el código para ejecutar en Wolfram Cloud, con enlaces a información en Wolfram Language y Wolfram MathWorld cuando esté disponible.
Operar edición grafo operateEditionGraph()
La operación edición de grafo permite crear un nuevo grafo dirigido o no dirigido, así como agregar y/o eliminar aristas y vértices. La operación recibe y devuelve siempre una matriz de adyacencia. En la Figura vemos el panel para edición con las acciones nuevo no dirigido y nuevo dirigido para crear un grafo nuevo; modificar para agregar y/o modificar vértices y aristas; borrar para eliminar vértices y aristas.
La opción posicionar no afecta cuando creamos un nuevo grafo, solo actúa en caso de modificación o borrado como veremos después.
Para las acciones hemos de pasar una lista de aristas en modo compacto. Esto quiere decir que, por ejemplo, la lista de aristas [1, 0], [2, 0] significa para un grafo dirigido las aristas "1🡒0, 2🡒0", mientras que para uno no dirigido son las aristas "1-0, 0-1, 2-0, 0-2". Un elemento de la lista con el segundo vértice con "-1", como por ejemplo [3, -1], significa el vértice "3" sin apuntar a otro vértice. La lista de aristas puede pasarse como [1, 0, "A"],[2, 0, "B"] indicando en la tercera posición el valor de la aristas, como veremos más abajo en un ejemplo.
{"error":"",
"matrix":
[[0,0,0],
[1,0,0],
[1,0,0]]}Se devuelve el resultado con la matriz de adyacencia creada en este caso para un nuevo grafo dirigido.
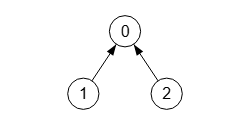
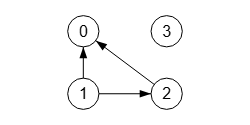
En la Figura vemos el grafo nuevo dirigido pasando la lista de aristas [1, 0], [2, 0].
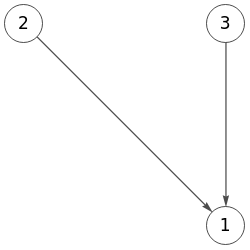
Para exportar a Wolfram un nuevo grafo usamos la función Graph con un argumento con la lista de aristas {2->1, 3->1}. Se usa a->b para una arista dirigida y a <-> b para una no dirigida. También puede usarse DirectedEdge[a, b] para dirigido y UndirectedEdge[a, b] para no dirigido.
En todos los casos no se reetiquetan los vértices, pues la matriz de adyacencia no puede representar las etiquetas de vértices, poniéndose como etiqueta el índice del vértice y no olvidando que en nuestra aplicación se inician en "0" y en Wolfram se inician en "1".
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center], VertexLabelStyle->Directive[Black, 17.5],
VertexStyle->White, EdgeLabelStyle->Directive[Black, 17.5], EdgeStyle->{{Black,Thickness[0.005]}}};
Graph[{2->1,3->1}, s]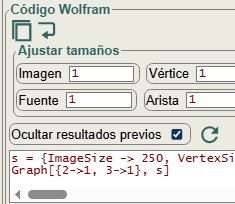
En la variable "s" pasamos el estilo del grafo, con la posibilidad de ajustar el tamaño del grafo, vértices, texto y grosor de aristas, mediante un factor sobre la unidad como se observa en la Figura.
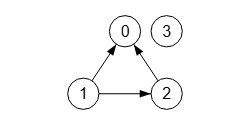
Con la acción para modificar un grafo pasamos en la lista de aristas aquellas que deseemos agregar o modificar las existentes. Si antes teníamos el grafo no dirigido creado con las aristas [1, 0], [2, 0], ahora vamos a modificar con [1, 2], [3, -1], lo que supone agregar la arista "1 🡒 2" y crear un nuevo vértice "3", pues el "-1" de [3, -1] significa un vértice aislado sin conexión con otros.
{"error":"",
"matrix":
[[0,0,0,0],
[1,0,1,0],
[1,0,0,0],
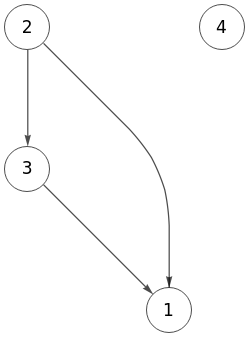
[0,0,0,0]]}El resultado se muestra en la Figura con esta matriz de adyacencia.
En la Figura al inicio de este apartado vimos la opción posicionar activada, diciendo que de estar activada entra en juego en caso de modificaciones y borrado. Con ella activada obtenemos el grafo modificado de la Figura mientras que desactivada obtenemos el grafo de la Figura. En caso de posicionar y posteriormente a la ejecución de la operación, la aplicación posiciona los nodos existentes tal como estaban en el grafo inicial. En los dos JSON siguiente vemos el primero con posicionar activada, donde se aplica nodeOffset al nodo "0" para reubicarlo tal como estaba al inicio. Y el otro JSON es con posicionar desactivada, con lo que no se aplica ninguna reubicación de nodos.
Con opción Posicionar activada: [{"index":0,"nodeOffset":"16.67","parent":[{"index":-1}]}, {"index":1,"parent":[{"index":0},{"index":2}]}, {"index":2,"parent":[{"index":0}]}, {"index":3,"parent":[{"index":-1}]}] Con opción Posicionar desactivada: [{"index":0,"parent":[{"index":-1}]}, {"index":1,"parent":[{"index":0},{"index":2}]}, {"index":2,"parent":[{"index":0}]}, {"index":3,"parent":[{"index":-1}]}]
Para exportar a Wolfram usaremos los recursos Table, EdgeQ, EdgeAdd y VertexAdd. Con Table iteramos por la lista de aristas para agregar con EdgeAdd solo aquellas que no existan mediante EdgeQ, pues si existe se creará en Wolfram una arista múltiple, algo que no contemplamos en nuestra aplicación dado que una matriz de adyacencia no puede representar aristas múltiples.
A continuación agregamos nuevos vértices con VertexAdd y finalmente presentamos el grafo resultante que puede ver en la Figura.
g = AdjacencyGraph[{{0,0,0},{1,0,0},{1,0,0}}, ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels->Placed["Name", Center],
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, DirectedEdges->True,
EdgeStyle->{{Black,Thickness[0.005]}}];
e = {2->3};
Table[If[Not[EdgeQ[g, i]], g = EdgeAdd[g, {i}]], {i, e}];
g = VertexAdd[g, {4}];
Graph[g]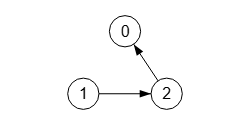
Con la edición borrar vértices o aristas pasamos la lista [1, 0], [3, -1] con la que borramos la arista "1 🡒 0" y el vértice "3", quedando el grafo como se observa en la Figura.
{"error":"",
"matrix":
[[0,0,0],
[0,0,1],
[1,0,0]]}
Para exportar a Wolfram usamos EdgeDelete para borrar aristas y VertexDelete para borrar vértices.
g = AdjacencyGraph[{{0,0,0,0},{1,0,1,0},{1,0,0,0},{0,0,0,0}}, ImageSize->250, VertexSize->{"Scaled", 0.13},
VertexLabels->Placed["Name", Center], VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
g = EdgeDelete[g, {2->1}];
g = VertexDelete[g, {4}];
Graph[g]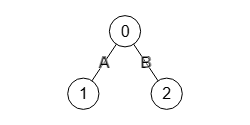
En la lista de aristas podemos pasar un tercer valor que será el de la etiqueta de la arista. Así con [1,0,"A"],[2,0,"B"] creamos un nuevo grafo, no dirigido en este ejemplo, con la arista "1 🡒 0" con la etiqueta "A" y la arista "2 🡒 0" con la etiqueta "B", como se observa en la Figura.
{"error":"",
"matrix":
[[null,"A","B"],
["A",null,null],
["B",null,null]]}Con etiquetas que no son números en las aristas se devuelve una matriz en modo null/value (ver más sobre esto en matriz de adyacencia).
Para exportar a Wolfram usamos Graph para crear un nuevo grafo y EdgeLabels para etiquetar las aristas, obteniendo el grafo que vemos en la Figura.
s = {ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels ->Placed["Name", Center], VertexLabelStyle -> Directive[Black, 17.5],
VertexStyle->White, EdgeLabelStyle->Directive[Black, 17.5], EdgeStyle->{{Black,Thickness[0.005]}}};
Graph[{2<->1, 3<->1}, EdgeLabels->{(2->1)->"A", (3->1)->"B"}, s]El codigo JavaScript que ejecuta operateEditionGraph() es el siguiente. Usa getMatrixModeValue() y isGraphDirected() vistos en un tema anterior. Y getEdges() que explicamos en el siguiente apartado.
// edition: newUndirected, newDirected, modify, delete
function operateEditionGraph({matrix=[], edges=[], edition="newUndirected"}) {
let dev = {error: "", matrix}, temp;
try {
if (edges.length>0) {
let n = matrix.length;
let directed = false;
let [modeValue, nullValue] = ["0/1", 0];
if (n===0 || edition.indexOf("new")===0) {
directed = edition==="newDirected";
if (edges.some(v => v.length===3 && (v[2]===null || typeof v[2]==="string"))) {
[modeValue, nullValue] = ["null/value", null];
} else if (edges.every(v => v.length===2 && v[1]===-1 || v.length===3 && typeof v[2]==="number")) {
[modeValue, nullValue] = ["0/number", 0];
} else if (edges.every(v => v.length===2 && v[1]===-1 || v.length===3 && typeof v[2]==="boolean")) {
[modeValue, nullValue] = ["false/true", false];
} else {
[modeValue, nullValue] = ["0/1", 0];
}
} else {
if (temp = isGraphDirected({matrix}), typeof temp==="string") throw new Error(temp);
directed = temp;
temp = getMatrixModeValue({matrix});
if (typeof temp==="string") throw new Error (temp);
[modeValue, nullValue] = temp;
}
if (edition!=="delete") {
if (edition==="modify") {
if (n===0) throw new Error(`The graph is empty, there is nothing to modify`);
if (temp = getEdges({matrix, edgesCompact:true}), typeof temp==="string") throw new Error(temp);
let actualEdges = temp;
if (actualEdges.length>0) {
actualEdges = actualEdges.map(v => v.join(","));
let copyEdges = edges.map(v => v.join(","));
edges = [];
for (let edge of copyEdges) {
if (!actualEdges.includes(edge)){
edges.push(edge.split(","));
}
}
}
} else {
matrix = [];
dev.matrix = matrix;
n = matrix.length;
}
let max = 0;
for (let edge of edges) {
let [i, j, v] = edge;
max = Math.max(max, i, j);
if (v!==undefined) {
edge[2] = modeValue==="0/1" ? 1 :
modeValue==="false/true" ? true :
modeValue==="0/number" ? (v===null || isNaN(v) ? 1 : Number(v)) :
v===null ? "" : typeof v==="boolean" || isNaN(v) ? v.toString() : v;
}
}
if (max>n-1) {
let m = max+1;
for (let i=0; i<n; i++) {
for (let j=n; j<m; j++) {
matrix[i][j] = nullValue;
}
}
for (let i=n; i<m; i++) {
matrix.push(Array.from({length:m}, () => nullValue));
}
}
for (let edge of edges) {
let [i, j, v] = edge;
if (j>-1) {
let value = v===undefined ? (modeValue==="false/true" ? true : modeValue==="null/value" ? "" : 1) : v;
matrix[i][j] = value;
if (!directed) {
matrix[j][i] = value;
}
}
}
} else {
for (let edge of edges) {
let [i, j] = edge;
if (i<matrix.length) {
if (j>-1) {
if (j<matrix.length) {
matrix[i][j] = nullValue;
if (!directed) matrix[j][i] = nullValue;
}
} else {
for (let k=0; k<matrix.length; k++) {
matrix[k].splice(i, 1);
}
matrix.splice(i, 1);
}
}
}
}
}
} catch(e){dev.error = `#Error operateEditionGraph(): ${clean(e.message)}`}
return dev;
}Obtener aristas getEdges()
En la seccion de acciones podemos encontrar el algoritmo getEdges() para obtener las aristas de un grafo. En la Figura se muestran los parámetros forzar no dirigido y salida compacta que explicaremos a continuación.
Para todos los algoritmos y otras partes de la aplicación he incluido el enlace con el icono que remite a temas en este sitio que explican cada parte, como a este mismo apartado.
El icono es el del mismo botón que antes tenía con la leyenda "Código", que ahora abre un panel emergente con el código JavaScript del algoritmo.
En la parte inferior se muestra el resultado al ejecutar el algoritmo, con el tiempo de ejecución y el propio resultado convertido en texto.
Veamos un ejemplo en ejecución para el grafo de la Figura.
0 7 9 0 0 14 0 0 10 15 0 0 0 0 0 11 0 2 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 9 0
Este grafo dirigido y ponderado se encuentra entre las muestras de la aplicación. También puede importarlo con esta matriz de adyacencia en formato SSV.
Time: 0 ms
Obtener aristas: {
"0,1":7, "0,2":9, "0,5":14,
"1,2":10, "1,3":15, "2,3":11,
"2,5":2, "4,3":6, "5,4":9}Al ejecutarlo sin activar forzar no dirigido y salida compacta obtenemos el resultado adjunto. Devuelve un objeto cuyas claves son las aristas y sus valores el valor de cada arista. Así, por ejemplo, "0,1":7 se refiere a la arista "0🡒1" que tiene el valor "7".
[[0,1],[0,2],[0,5], [1,2],[1,3],[2,3], [2,5],[4,3],[5,4]]
En caso de activar salida compacta obtenemos un array en lugar de un objeto. Así, por ejemplo, [0, 1] se refiere a la arista "0🡒1". En cualquier caso con [i, j] siempre entenderemos "i🡒j" en un grafo dirigido e "i-j" en uno no dirigido. Vea que con este parámetro activado perdemos el valor de la arista.
Time: 0 ms
Obtener aristas: {
"0,1":7, "1,0":7, "0,2":9,
"2,0":9, "0,5":14, "5,0":14,
"1,2":10, "2,1":10, "1,3":15,
"3,1":15, "2,3":11, "3,2":11,
"2,5":2, "5,2":2, "4,3":6,
"3,4":6, "5,4":9, "4,5":9}Si activamos forzar no dirigido sobre un grafo dirigido, sin usar salida compacta, obtenemos un objeto con las claves. Así, por ejemplo, tenemos "0,1":7, "1,0":7 que, para un no dirigido, viene a ser la arista "0-1" con valor "7".
La aplicación permite exportar las distintas acciones a Wolfram Cloud, como explicamos en un tema anterior cuando exponíamos las estructuras de datos. Como se observa en la Figura, al ejecutar el ejemplo anterior obtenemos el código Wolfram y un enlace para ir a Wolfram Cloud, donde tiene que abrir su sesión y pegar ese código que vemos también a continuación. Hacemos un ajuste de tamaños de imagen y de vértices para que el resultado tenga un aspecto lo más similar posible al grafo de nuestra aplicación.
g = AdjacencyGraph[{{0,1,1,0,0,1},{0,0,1,1,0,0},{0,0,0,1,0,1},{0,0,0,0,0,0},{0,0,0,1,0,0},{0,0,0,0,1,0}},
ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels->{1->Placed[0,Center],
2->Placed[1,Center], 3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center],
6->Placed[5,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(1->2)->7, (1->3)->9, (2->3)->10, (2->4)->15, (3->4)->11, (5->4)->6, (6->5)->9, (1->6)->14, (3->6)->2},
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}]
EdgeList[g]
En la Figura vemos el resultado en Wolfram Cloud, presentando el grafo original que es estructuralmente igual que el de la Figura obtenido en nuestra aplicación.
Y también ofrece la lista de aristas {1🡒2, 1🡒3, 1🡒6, 2🡒3, 2🡒4, 3🡒4, 3🡒6, 5🡒4, 6🡒5} que es la misma que la que obtuvimos [[0, 1], [0, 2], [0, 5], [1, 2], [1, 3], [2, 3], [2, 5], [4, 3], [5, 4]] si tenemos en cuenta que en Wolfram los índices se inician en 1 y en nuestra aplicación en 0. Tenga en cuenta que los nodos están etiquetados desde 0 como en nuestra aplicación, pero en Wolfram se inician en 1.
En el texto anterior he usado la flecha "🡒" en lugar de la que usa Wolfram que es el UNICODE 0F3D5 "", tal como explica en \[DirectedEdge] para una arista dirigida, pues no es representable directamente en los navegadores dado que está en una sección de uso privado en Unicode.
Nuestra aplicación nunca utiliza internamente caracteres flecha para representar una arista, pues tal como hemos explicado, el array [1, 2] significa "1🡒2" en un grafo dirigido y "1-2" o "2-1" en un grafo no dirigido.
En el código de Wolfram puede escribirse la relación como a \[DirectedEdge] b o con DirectedEdge[a, b] o bien con a->b para dirigido, como por ejemplo Graph[{1\[DirectedEdge]2, DirectedEdge[1,3], 2->3}, VertexLabels->"Name"] que usando las tres formas creará el grafo dirigido que vemos en la Figura.
Y a \[UndirectedEdge] b o con DirectedEdge[a, b] o bien con a <-> b para no dirigido con el ejemplo Graph[{1\[UndirectedEdge]2, UndirectedEdge[1, 3], 2<->3}, VertexLabels->"Name"] que creará un grafo como el anterior pero sin flechas en las aristas para grafo no dirigido.
En el código siguiente de getEdges() usamos la operación isGraphDirected() que ya vimos en un tema anterior.
function getEdges({matrix=[], forceUndirected=false, edgesCompact=false}) {
let result = edgesCompact ? [] : {};
try {
let n = matrix.length;
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
for (let i=0; i<n; i++) {
let k = (edgesCompact && !directed) ? i : 0;
for (let j=k; j<n; j++) {
if (matrix[i][j]!==0) {
if (edgesCompact) {
result.push([i, j])
} else {
result[`${i},${j}`] = matrix[i][j];
}
}
if (!edgesCompact) {
if (!directed) {
if (matrix[j][i]!==0) result[`${j},${i}`] = matrix[j][i];
} else if (forceUndirected && matrix[i][j]!==0) {
result[`${j},${i}`] = matrix[i][j];
}
}
}
}
} catch(e) {result = e.message}
return result;
}El argumento edgesCompact se refiere al modo de salida compacta que hemos explicado más arriba. Y también forceUndirected a forzar no dirigido.
Operar contracción grafo operateContractionGraph()
La operación contracción entre dos nodos "a" y "b" (controles índice 1 e índice 2 de la Figura), con o sin arista no dirigida "a-b" o dirigida "a🡒b", fusionará ambos en un único nodo traspasando las aristas del nodo "b" al nodo "a". Si las aristas tienen valores y si hay un tercer nodo "c" de tal forma que existen las aristas "a-c" y "b-c" (o "a🡒c" y "b🡒c"), al valor fusionado se le puede aplicar alguna opción según el control tipo valor fusionado entre poner como valor ninguno, primero, último, mínimo, máximo, suma o media de los valores de esas terceras aristas. Si hay una arista entre nodos "a-b" (o "a🡒b") entonces se creará un autobucle "a-a" (o "a🡒a"), a no ser que se marque la opción omitir autobucles. Más abajo veremos un ejemplo con la opción índices.
Con el control posicionar activado se reubicarán los nodos resultantes tras la operación en las mismas ubicaciones que inicialmente tenían.
0 10 20 0 0 10 0 30 40 50 20 30 0 0 60 0 40 0 0 70 0 50 60 70 0
Por ejemplo, con el grafo no dirigido y ponderado de la Figura contraemos los nodos "3" y "4", que forman en este caso la arista no dirigida "3-4", pudiendo importar el ejemplo con esta matriz de adyacencia, que al ser un grafo ponderado tiene la mariz de adyacencia en modo valores 0/number.
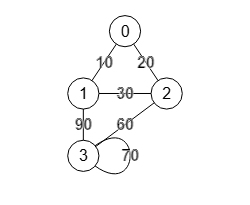
El resultado obtenido tras contraer la arista "3-4", con valor "70", se muestra en la Figura. Se elimina el nodo "4" creándose un autobucle "3-3" con valor "70" que era el valor de la arista "3-4". La arista "4-2" con valor "60" pasa a ser ahora "3-2" con el mismo valor. Como habían dos aristas "3-1" con valor "40" y "4-1" con valor "50", se creará una única arista fusionada "3-1" con valor suma 40+50 = "90" pues hemos optado por este valor fusionado.
Observe como al estar activada la opción posicionar, los nodos resultantes, especialmente el nodo "3", aparecen en la misma ubicación que los iniciales.
{"error":"",
"matrix":
[[0,10,20,0],
[10,0,30,90],
[20,30,0,60],
[0,90,60,70]],
"labels":[[0],[1],[2],[3,4]]
}Este el el resultado obtenido, con la matriz de adyacencia del grafo con la contracción "3-4". El campo "labels" contiene las etiquetas tras la contracción, así el índice 3 en el nuevo grafo tiene la etiqueta [3,4] de la contracción de esos nodos.
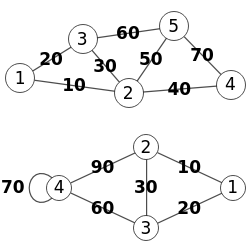
Para exportar a Wolfram usamos EdgeContract, que cuando se trata de un grafo ponderado se crea el grafo con WeightedAdjacencyGraph, pasando la matriz que vimos más arriba cambiando los "0" por "∞". En la Figura vemos el grafo inicial y el resultado al contraer la arista "4-5", correspondiente a nuestro ejemplo "3-4" pues en Wolfram los índices se inician en 1.
Con grafos ponderados Wolfram suma las aristas "4-2" con valor "40" y "5-2" con valor "50" para fusionar en la arista "4-2" con valor "90". En nuestra aplicación caben varias alternativas para fusionar dos aristas, como dijimos más arriba que era primero, último, mínimo, máximo, suma o media, pero en Wolfram con grafos ponderados sólo cabe de forma obligatoria la suma.
Wolfram no considera el autobucle y se lo agregamos con las sentencias f = First[e] <-> First[e] para crear la arista "4-4" de autobucle, g = EdgeAdd[g, f] para añadirla al grafo contraido y Graph[g, EdgeWeight->{f->w}] para darle el peso "70" tras obtener ese peso con w = PropertyValue[{g, e}, EdgeWeight] sobre la arista "4-5".
g = WeightedAdjacencyGraph[{{∞,10,20,∞,∞},{10,∞,30,40,50},{20,30,∞,∞,60},{∞,40,∞,∞,70},{∞,50,60,70,∞}}, ImageSize -> 250,
VertexSize -> {"Scaled", 0.13}, VertexLabels -> Placed["Index", Center], VertexLabelStyle -> Directive[Black,17.5],
EdgeLabelStyle -> Directive[Black,17.5,Bold], EdgeLabels -> "EdgeWeight", VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}]
e = 4 <-> 5;
f = First[e] <-> First[e];
w = PropertyValue[{g, e}, EdgeWeight];
g = EdgeContract[g, e];
g = EdgeAdd[g, f];
Graph[g, EdgeWeight->{f -> w}]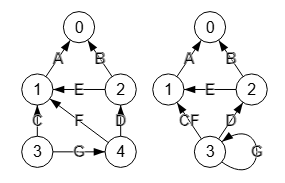
Veamos ahora un ejemplo con un grafo dirigido y no ponderado, pero con aristas etiquetadas. En la Figura vemos el grafo inicial y el resultado de la contracción de la arista "3🡒4", teniendo en cuenta desactivar la opción posicionar.
null null null null null "A" null null null null "B" "E" null null null null "C" null null "G" null "F" "D" null null
Esta es la matriz de adyacencia del grafo inicial con el modo valores null/value que permite etiquetar las aristas con caracteres alfanuméricos.
{"error":"",
"matrix":
[[null,null,null,null],
["A",null,null,null],
["B","E",null,null],
[null,"CF","D","G"]],
"labels":[[0],[1],[2],[3,4]]}Este es el resultado obtenido al contraer la arista "3🡒4" que produce el segundo grafo de la Figura, observando que las aristas "3🡒1" con valor "C" y "4🡒1" con valor "F" se fusionan en la arista "3🡒1" con valor "CF", pues hemos optado por sumar valores que para caracteres se concatenan. La arista "3🡒4" se convierte en el autobucle "3🡒3" con valor "G".
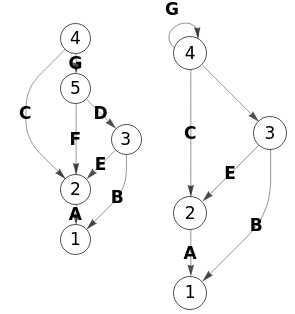
En la Figura vemos el grafo inicial y el grafo con la contracción de la arista "4🡒5" en Wolfram.
Hemos ajustado el tamaño de la imagen y de los vértices con un factor de 0.5 pues aparecían excesivamente grandes. La exportación es igual que la que vimos en el ejemplo anterior, usando las funciones de Wolfram PropertyValue, EdgeContract, EdgeAdd y Graph.
La arista "4🡒3" no tiene la etiqueta "D" que tiene la arista equivalente "3🡒2" de nuestra aplicación pues Wolfram no traslada etiquetas con EdgeContract. De la misma forma la arista "4🡒2" no concatena los valores "CF" como en nuestra aplicación.
g = AdjacencyGraph[{{0,0,0,0,0},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}}, ImageSize->125, VertexSize->{"Scaled", 0.13},
VertexLabels->Placed["Index", Center], VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(2->1)->"A", (3->1)->"B", (3->2)->"E", (4->2)->"C", (4->5)->"G", (5->2)->"F", (5->3)->"D"}, VertexStyle->White,
DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
e = 4->5;
f = First[e]->First[e];
w = PropertyValue[{g, e}, EdgeLabels];
g = EdgeContract[g, e];
g = EdgeAdd[g, f];
Graph[g, EdgeLabels->{f->w}]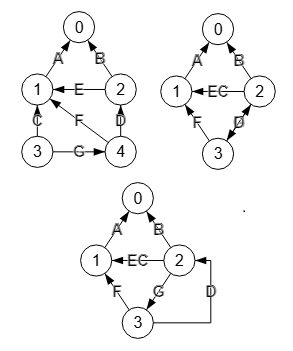
En la Figura vemos el mismo grafo con aristas etiquetadas del ejemplo anterior, ahora contrayendo los vértices "2" y "3" sin arista entre ellos, con la opción posicionar desactivada, incluyéndose en la misma imagen el grafo resultado y la reubicación de la arista "3🡒2" con etiqueta "D".
null null null null null "A" null null null null "B" "E" null null null null "C" null null "G" null "F" "D" null null
Esta es la matriz de adyacencia en modo valores null/value para el grafo inicial.
{"error":"",
"matrix":
[[null,null,null,null],
["A",null,null,null],
["B","EC",null,"G"],
[null,"F","D",null]],
"labels":[[0],[1],[2,3],[4]]}Y este el resultado obtenido. La contracción de vértices funciona de forma similar que la de aristas, pero no se crea un autobucle pues no hay arista entre los vértices.
El siguiente JSON reubica la arista "3🡒2" con etiqueta "D":
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0,"value":"A"}]},
{"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"EC"},{"index":3,"value":"G"}]},
{"index":3,"parent":[{"index":1,"value":"F"},{"index":2,"value":"D","lineOffset":2.34}]}
],
"config":{
"markerEnd":"arrow"
}}
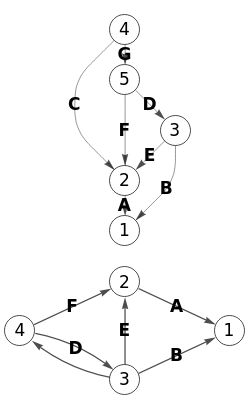
Exportamos a Wolfram como se observa en la Figura, donde el primer grafo es el inicial y el segundo es el resultado de la contracción de los nodos "3" y "4", correspondiente a los nodos "2" y "3" de nuestro ejemplo pues en Wolfram los índices se inician en "1" y en nuestra aplicación en "0". Las arista "3🡒2" con etiqueta "E" en Wolfram se corresponde con la "2🡒1" con etiqueta "EC" en nuestra aplicación, pero Wolfram no concatena valores de etiquetas. La arista "3🡒4" sin etiqueta en Wolfram se corresponde con "2🡒3" con etiqueta "G" en nuestra aplicación, pero Wolfram no traslada el valor de la etiqueta "G" que inicialmente estaba en la arista "4🡒5".
Para contraer vértices se usa VertexContract.
g = AdjacencyGraph[{{0,0,0,0,0},{1,0,0,0,0},{1,1,0,0,0},{0,1,0,0,1},{0,1,1,0,0}},
ImageSize->250, VertexSize->{"Scaled", 0.13}, VertexLabels->Placed["Index", Center],
VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(2->1)->"A", (3->1)->"B", (3->2)->"E", (4->2)->"C", (4->5)->"G", (5->2)->"F", (5->3)->"D"},
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
v = {3, 4};
VertexContract[g, v]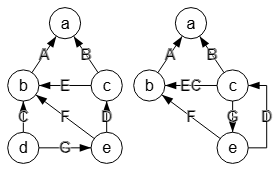
Observe que en la Figura los índices de los nodos tras la contracción de vértices "2" y "3" se renumeran, pues el "0" y el "1" no resultan afectados, el "2" y el "3" se fusionan en el "2" y el "4" pasa a ser ahora el "3". Hay que tener en cuenta que las ediciones se realizan sobre la matriz de adyacencia, donde no se pueden etiquetar los nodos y las etiquetas que aparecen se corresponden con sus índices en la matriz de adyacencia.
En la Figura vemos la ejecución del mismo grafo pero con nodos etiquetados, ejecutándose la operación de contraer nodos o aristas usando el botón , operación que se realiza sobre el JSON y no sobre la matriz de adyacencia. Contraer los vértices "2" y "3" en nuestro ejemplo anterior equivale a hacerlo con los vértices etiquetados "c" y "d", observando en este caso que las etiquetas de nodos no resultan afectadas, pues sólo la etiqueta "d" desaparece al fusionarse con la "c", si no usamos la opción mantener valores de nodos de esa operación en el JSON pues en otro caso la etiqueta "c" se convierte en "cd". Aunque internamente sigue conservando los índices de nodos igual que en la matriz de adyacencia. El JSON siguiente configura el grafo inicial con los nodos etiquetados en el propio JSON:
{"nodes":[
{"index":0,"value":"a","parent":[{"index":-1}]},
{"index":1,"value":"b","parent":[{"index":0,"value":"A"}]},
{"index":2,"value":"c","parent":[{"index":0,"value":"B"},{"index":1,"value":"E"}]},
{"index":3,"value":"d","parent":[{"index":1,"value":"C"},{"index":4,"value":"G"}]},
{"index":4,"value":"e","parent":[{"index":1,"value":"F"},{"index":2,"value":"D"}]}
],
"config":{
"markerEnd":"arrow"
}}
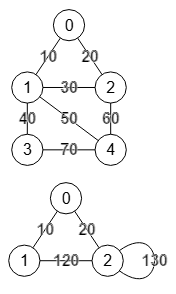
En la Figura vemos el mismo grafo inicial del inicio de este apartado y la contracción de la lista de nodos "2,3,4" que podemos incluir en la opción índices que veíamos en la Figura. Las aristas "3-1", "4-1" y "2-1" se suman 40+50+30=120 siendo el valor de la nueva arista "2-1". Observe que ahora es el nodo "2" el que agrupa "2,3,4". Las aristas dentro de esa lista "3-4" y "4-2" con valores 60 y 70 se suman para el autobucle "2-2" con valor 130. Con esta opción podemos contraer más de dos nodos de una vez.
{"error":"",
"matrix":
[[0,10,20],
[10,0,120],
[20,120,130]],
"labels":[[0],[1],[2,3,4]]}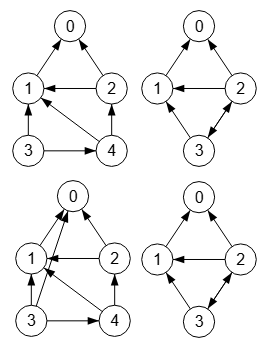
La contracción no podría tener una operación inversa, aunque en Wolfram MathWorld encontramos la referencia Edge Splitting diciendo que es la inversa de EdgeContract. Sin embargo Wolfram no expone una función de la forma EdgeSplitting. Como ejemplo vemos la Figura donde en la parte superior izquierda aparece un grafo y a la derecha la contracción de los nodos "2" y "3".
Primer grafo 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1 0 0 Segundo grafo con arista "3🡒0" 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 1 0 0 1 0 1 1 0 0
En la parte inferior izquierda de la Figura agregamos la arista "3🡒0" y vemos que produce la misma contracción de los nodos "2" y "3". Por tanto la inversa de una contracción podría tener más de una alternativa por lo que no veo forma de recuperar el original de una contracción. En el siguiente apartado veremos la operación división (splitting) donde si se puede aplicar la inversa reunión (unsplitting), exponiendo unas aclaraciones al respecto.
El código JavaScript para ejecutar operateContractionGraph() es el siguiente, usando la funciones isGraphDirected() para saber si el grafo es dirigido y getMatrixModeValue() para obtener el modo valores de la matriz de adyacencia.
function operateContractionGraph({matrix=[], index1=0, index2=0, typeMergedValue="none"}) {
let dev = {error: "", matrix}, temp;
try {
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
let temp = getMatrixModeValue({matrix});
if (typeof temp==="string") throw new Error (temp);
let [modeValue, nullValue] = temp;
let n = matrix.length;
if (!(index1>-1 && index1<n)) throw new Error(`Index '${index1}' is wrong`);
if (!(index2>-1 && index2<n)) throw new Error(`Index '${index2}' is wrong`);
for (let j=0; j<matrix[index1].length; j++) {
let value1 = matrix[index1][j];
let value2 = matrix[index2][j];
let value = value1 || value2;
if (value1!==nullValue && value2!==nullValue) {
if (temp = valueMerged([value1, value2], typeMergedValue, modeValue), temp.error) throw new Error(temp.error);
value = temp.value;
}
matrix[index1][j] = value;
if (!directed) matrix[j][index1] = value;
}
if (directed) {
for (let i=0; i<matrix.length; i++) {
let value1 = matrix[i][index1];
let value2 = matrix[i][index2];
let value = value1 || value2;
if (value1!==nullValue && value2!==nullValue) {
if (temp = valueMerged([value1, value2], typeMergedValue, modeValue), temp.error) throw new Error(temp.error);
value = temp.value;
}
matrix[i][index1] = value;
}
}
for (let i=0; i<matrix.length; i++) {
matrix[i].splice(index2, 1);
}
matrix.splice(index2, 1);
} catch(e){dev.error = `#Error operateContractionGraph(): ${clean(e.message)}`}
return dev;
}Otra función auxiliar usada es valueMerged() que fusiona los valores según el tipo primero, último, máximo, mínimo, suma y promedio.
function valueMerged(values=[], type="none", modeValue="0/1"){
let dev = {error: "", value: null};
try {
let activeOper = modeValue==="null/value" ? "": modeValue==="false/true" ? false : 0;
values = values.map(v => v || activeOper);
if (type==="first"){
dev.value = values[0];
} else if (type==="last"){
dev.value = values[values.length-1];
} else if (type==="min"){
dev.value = modeValue==="0/number" ? Math.min(...values) : values[0];
} else if (type==="max"){
dev.value = modeValue==="0/number" ? Math.max(...values) : values[values.length-1];
} else if (type==="sum"){
dev.value = modeValue==="0/number" ? values.reduce((p,v) => (p+=v, p), 0) :
modeValue==="null/value" ? values.join("") :
modeValue==="false/true" ? true :
1;
} else if (type==="mean"){
dev.value = modeValue==="0/number" ? values.reduce((p,v) => (p+=v, p), 0) / 2 :
modeValue==="null/value" ? values.reverse().join("") :
modeValue==="false/true" ? true :
1;
} else {
dev.value = modeValue==="false/true" ? true : modeValue==="null/value" ? "" : 1;
}
} catch(e){dev.error = `#Error valueMerged(): ${clean(e.message)}`}
return dev;
}Operar división grafo operateSplittingGraph()
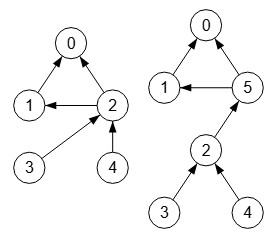
En un grafo dirigido la operación división (splitting) de un nodo se basa en detectar las aristas salientes de ese nodo, traspasándolas a un nuevo nodo a crear, apuntando el nodo anterior a este nuevo nodo. Como entran en juego la dirección de las aristas es por lo que sólo se aplica a grafos dirigidos.
0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 1 0 0
Empecemos con un grafo dirigido no etiquetado que se muestra en la parte izquierda de la Figura. En nuestra aplicación este grafo tiene un modo valores 0/1. En los subapartados siguientes veremos la división en modo "0/number" y en modo "null/value".
{"error":"",
"matrix":
[[0,0,0,0,0,0],
[1,0,0,0,0,0],
[0,0,0,0,0,1],
[0,0,1,0,0,0],
[0,0,1,0,0,0],
[1,1,0,0,0,0]]}Ejecutamos la operación para dividir el nodo "2" obteniéndose este resultado que se observa en el grafo de la derecha de la Figura. Observamos que se ha creado un nuevo nodo "5" y nueva arista "2🡒5", traspasando las aristas "2🡒0" y "2🡒1" a "5🡒0" y "5🡒1".
En la Figura vemos las opciones para ejecutar la división (splitting) de un nodo (índice 1) así como la operación inversa reunión (unsplitting) marcando la opción Reunir, en cuyo caso hay que seleccionar dos nodos índice 1 y índice 2 que deben formar una arista con la dirección "índice 1 🡒 índice 2". Para reunir dos nodos "a" y "b" tienen que cumplirse que el nodo "a" debe tener una única arista saliente "a🡒b" y el nodo "b" esa misma única arista entrante.
La opción tipo valor fusionado se aplica a la división al valor que se le asigna a la nueva arista "2🡒5" en el ejemplo anterior, aunque no aplica pues el modo valores "0/1" no tiene etiquetas de aristas. En otro caso esa nueva arista puede tomar ningún valor o el valor del tipo de sus aristas entrantes: primero, último, mínimo, máximo, suma y promedio. Luego veremos ejemplos en modos "0/number" y "null/value".
En caso de estar activada la opción posicionar, tras la ejecución del algoritmo sobre la matriz de adyacencia se reposicionan los nodos en las posiciones que tenían inicialmente. En todos los ejemplos que vemos esa opción la hemos desactivado pues se observa mejor el resultado.
En Wolfram MathWorld encontramos la referencia Edge Splitting diciendo que es la inversa de EdgeContract. Sin embargo Wolfram no expone una función del tipo EdgeSplitting. Nuestra operación división o splitting parece inversamente similar a la contracción, es decir la contracción equivaldría a la reunión, pero nada tiene que ver pues:
- La división o reunión tal como la definimos sólo se aplica a grafos dirigidos, mientras que la contracción no tiene esta limitación.
- La contracción fusiona dos nodos en un único nodo. Su operación inversa sería separar ese nodo en dos nodos, lo que podría asimilarse a la división pero no queda claro cuáles son las aristas entrantes y salientes, y con más razón en un grafo no dirigido.
- La reunión se aplica también sólo a grafos dirigidos, debiendo existir una única arista "a🡒b" entre esos dos nodos "a" y "b", lo que no supone que se asimile a la contracción pues no hay limitaciones de ese tipo y donde pueden usarse grafos no dirigidos.
- La contracción entre dos nodos "a🡒b" crea autobucle "a🡒a" cuando hay una arista entre dos nodos, mientras que la reunión "a🡒b" no crea autobucle.
Además en el apartado anterior pusimos unas consideraciones acerca de la inexistencia de la inversa de la contracción.
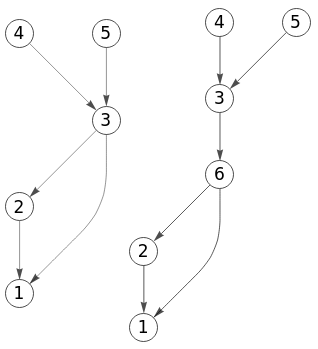
No encuentro en Wolfram una función para ejecutar la operación división (splitting), por lo que he tenido que construirla. Posiblemente el código siguiente pueda simplificarse, pero es lo que he podido llevar a cabo.
Con n = Max[VertexList[g]] vemos cuál el índice del último nodo del grafo inicial pues el nuevo nodo tendrá indice "n+1". En v=3 nos pasan el nodo que vamos a dividir. Con e = EdgeList[g] obtenemos {2🡒1, 3🡒1, 3🡒2, 4🡒3, 5🡒3} que son todas las aristas del grafo inicial. Con out = Select[e,First[#]==v&] seleccionamos las aristas salientes del nodo "3" obteniendo {3🡒1, 3🡒2}, aristas que borramos con g = EdgeDelete[g, out]. Con out2 = ReplaceAll[out, v->n+1] modificamos en la lista anterior el "3" por "n+1", que es "6", obteniendo {6🡒1, 6🡒2}, lista de aristas que agregamos con g = EdgeAdd[g, out2]. Finalmente con EdgeAdd[g, {v->n+1}] agregamos la arista "3🡒6".
g = AdjacencyGraph[{{0,0,0,0,0},{1,0,0,0,0},{1,1,0,0,0},{0,0,1,0,0},{0,0,1,0,0}}, ImageSize->188,
VertexSize->{"Scaled", 0.08}, VertexLabels->Placed["Index", Center], VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
Catch[
If[Not[DirectedGraphQ[g]], Throw["Splitting operation is not defined for undirected graphs"]];
n = Max[VertexList[g]];
v = 3;
e = EdgeList[g];
out = Select[e,First[#]==v&];
out2 = ReplaceAll[out, v->n+1];
g = EdgeDelete[g, out];
g = EdgeAdd[g, out2];
EdgeAdd[g, {v->n+1}]
]
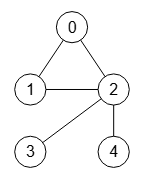
En el código Wolfram anterior usamos Catch y Throw para lanzar un error si el grafo fuera no dirigido, lo que se comprueba con Not[DirectedGraphQ[g]], observándolo con el grafo no dirigido de la Figura.
0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 0 0 0 1 0 0
La operación inversa a la división (splitting) es la reunión (unsplitting) que se ejecuta marcando la opción Reunir (ver Figura) y seleccionando la arista "2🡒5" en la aplicación ("3🡒6" en Wolfram). En el desplegable siguiente exponemos sólo el código Wolfram de la reunión, obteniéndose las inversas de los grafos en las imágenes de la Figura en la aplicación y de la Figura en Wolfram, que no exponemos para abreviar.
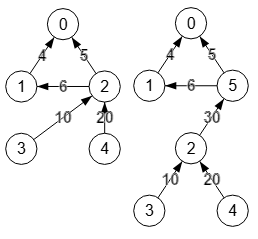
En la Figura vemos a la izquierda un grafo dirigido ponderado, en modo valores 0/number. Y a la derecha el resultado de la división (splitting) del nodo "2". Usamos la opción posicionar desactivada, tal como podemos ver en la Figura.
0 0 0 0 0 4 0 0 0 0 5 6 0 0 0 0 0 10 0 0 0 0 20 0 0
Esta es la matriz de adyacencia del grafo ponderado inicial. Vemos que el resultado obtenido crea un nuevo nodo "5", traspasando las aristas "2🡒0" y "2🡒1" a "5🡒0" y "5🡒1", creando la nueva arista "2🡒5" cuyo valor "30" es la suma de la aristas "3🡒2" con valor "10" y "4🡒2" con valor 20. Hemos optado por la suma para el tipo valor fusionado, una de las opciones que vimos en la Figura. Podíamos haber tomado ninguno, primero, último, mínimo, máximo o media.
{"error":"",
"matrix":
[[0,0,0,0,0,0],
[4,0,0,0,0,0],
[0,0,0,0,0,30],
[0,0,10,0,0,0],
[0,0,20,0,0,0],
[5,6,0,0,0,0]]}La aplicación devuelve este resultado, con la nueva matriz de adyacencia.
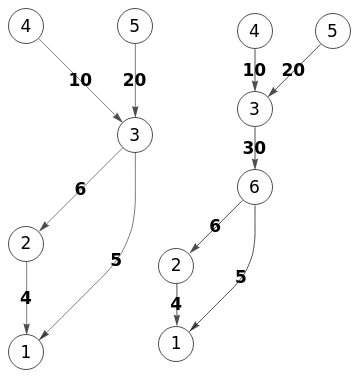
Exportando a Wolfram vemos en la Figura a la izquierda el grafo inicial. Y a la derecha el resultado de la división del nodo "3", que se corresponde con el "2" en nuestra aplicación, observando que se obtiene el mismo resultado.
Hemos ajustado el tamaño del grafo tal como se observa en la Figura.
El código es igual que el visto antes en el ejemplo del modo "0/1". Pero ahora además hemos de poner los valores de las nuevas etiquetas (o pesos).
g = WeightedAdjacencyGraph[{{∞,∞,∞,∞,∞},{4,∞,∞,∞,∞},{5,6,∞,∞,∞},{∞,∞,10,∞,∞},{∞,∞,20,∞,∞}}, ImageSize->200,
VertexSize->{"Scaled", 0.1}, VertexLabels->Placed["Index", Center], VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], EdgeLabels->"EdgeWeight", VertexStyle->White,
DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
Catch[
If[Not[DirectedGraphQ[g]], Throw["Splitting operation is not defined for undirected graphs"]];
n = Max[VertexList[g]];
v = 3;
e = EdgeList[g];
out = Select[e,First[#]==v&];
out2 = ReplaceAll[out, v->n+1];
w = Table[i->PropertyValue[{g, i}, EdgeWeight], {i,e}];
vv = Select[w, Last[First[#]]==v&];
ws = Table[Last[i], {i, vv}];
op = "sum";
s = If[op=="sum",Sum[i, {i,ws}], If[op=="first", First[ws], If[op=="last", Last[ws], If[op=="max", Max[ws], If[op=="min", Min[ws], If[op=="mean", Mean[ws]]]]]]];
ww = Select[w, First[First[#]]==v&];
w2 = ReplaceAll[ww, (DirectedEdge[x_, y_]->z_)->DirectedEdge[n+1, y]-> z];
g = EdgeDelete[g, out];
g = EdgeAdd[g, out2];
g = EdgeAdd[g, {v->n+1}];
g = Graph[g, EdgeWeight->w2];
Graph[g, EdgeWeight->{DirectedEdge[v,n+1]->s}]
]La operación inversa a la división (splitting) es la reunión (unsplitting) que se ejecuta marcando la opción Reunir (ver Figura) y seleccionando la arista "2🡒5" en la aplicación ("3🡒6" en Wolfram). En el desplegable siguiente exponemos sólo el código Wolfram de la reunión, obteniéndose las inversas de los grafos en las imágenes de la Figura en la aplicación y de la Figura en Wolfram, que no exponemos para abreviar.
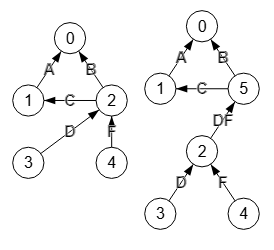
En la Figura vemos a la izquierda un grafo dirigido con aristas etiquetadas (no ponderado), con modo valores null/value. Y a la derecha el resultado de la división del nodo "2". Usamos la opción posicionar desactivada y la suma para el tipo valor fusionado, tal como podemos ver en la Figura.
null null null null null "A" null null null null "B" "C" null null null null null "D" null null null null "F" null null
Esta es la matriz de adyacencia del grafo inicial en modo valores "null/value". Vemos que la división es igual que las vistas en los modos "0/1" y "0/number", solo que la operación "suma" para valores que no son números se usa como contatenación de cadenas. Así la suma y la media de "D" y "F" será "DF" y para el mínimo o máximo se usará el primero "D" o último "F".
{"error":"",
"matrix":
[[null,null,null,null,null,null],
["A",null,null,null,null,null],
[null,null,null,null,null,"DF"],
[null,null,"D",null,null,null],
[null,null,"F",null,null,null],
["B","C",null,null,null,null]]}Este es el resultado obtenido.
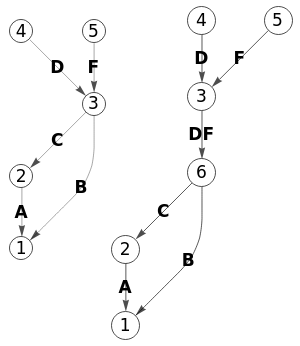
Exportamos a Wolfram el grafo inicial a la izquierda de la Figura con el resultado de la división del nodo "3" ("2" en nuestra aplicación) en el grafo de la derecha. El codigo es similar al visto antes, solo cambia lo que respecta a las operaciones para el valor fusionado.
g = AdjacencyGraph[{{0,0,0,0,0},{1,0,0,0,0},{1,1,0,0,0},{0,0,1,0,0},{0,0,1,0,0}}, ImageSize->188, VertexSize->{"Scaled", 0.08},
VertexLabels->Placed["Index", Center], VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->{(2->1)->"A", (3->1)->"B", (3->2)->"C", (4->3)->"D", (5->3)->"F"}, VertexStyle->White, DirectedEdges->True,
EdgeStyle->{{Black,Thickness[0.005]}}];
Catch[
If[Not[DirectedGraphQ[g]], Throw["Splitting operation is not defined for undirected graphs"]];
n = Max[VertexList[g]];
v = 3;
e = EdgeList[g];
l = Table[i ->PropertyValue[{g,i}, EdgeLabels], {i, e}];
lm = Select[l, Last[First[#]]==v&];
m = Table[Last[i], {i, lm}];
op = "sum";
s = If[Or[op=="sum" , op=="mean"],StringJoin[m], If[Or[op=="first", op=="min"], First[m], If[Or[op=="last", op=="max"], Last[m]]]];
el = ReplaceAll[l, (DirectedEdge[v, y_]->z_)->DirectedEdge[n+1, y]-> z];
out = Select[e,First[#]==v&];
out2 = ReplaceAll[out, v->n+1];
g = EdgeDelete[g, out];
g = EdgeAdd[g, out2];
g = EdgeAdd[g, {v->n+1}];
g = Graph[g, EdgeLabels->el];
g = Graph[g, EdgeLabels->{DirectedEdge[v, n+1]->s}]
]La operación inversa a la división (splitting) es la reunión (unsplitting) que se ejecuta marcando la opción Reunir (ver Figura) y seleccionando la arista "2🡒5" en la aplicación ("3🡒6" en Wolfram). En el desplegable siguiente exponemos sólo el código Wolfram de la reunión, obteniéndose las inversas de los grafos en las imágenes de la Figura en la aplicación y de la Figura en Wolfram, que no exponemos para abreviar.
El código JavaScript para ejecutar operateSplittingGraph() es el siguiente, usando la funciones isGraphDirected() para saber si el grafo es dirigido y getMatrixModeValue() para obtener el modo valores de la matriz de adyacencia. Otra función auxiliar usada es valueMerged() que fusiona los valores según el tipo primero, último, máximo, mínimo, suma y promedio, que ya expusimos en un apartado anterior.
El argumento unsplitting nos permite dividir cuando es falso o reunir cuando es verdadero.
function operateSplittingGraph({matrix=[], index1=0, index2=0, typeMergedValue="none", unsplitting=false}) {
let dev = {error: "", matrix}, temp;
try {
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
if (!directed) throw new Error(`Splitting operation is not defined for undirected graphs`);
let temp = getMatrixModeValue({matrix});
if (typeof temp==="string") throw new Error (temp);
let [modeValue, nullValue] = temp;
let n = matrix.length;
if (!unsplitting) {
let indexesOut = [];
for (let j=0; j<n; j++) {
if (matrix[index1][j]!==nullValue) {
indexesOut.push(j);
}
}
if (indexesOut.length>0) {
for (let i=0; i<n; i++) {
matrix[i].push(nullValue);
}
let row = Array.from({length: n+1}, () => nullValue);
matrix.push(row);
for (let j of indexesOut) {
matrix[n][j] = matrix[index1][j];
matrix[index1][j] = nullValue;
}
let values = [];
for (let j=0; j<n; j++) {
if (matrix[j][index1]!==nullValue) {
values.push(matrix[j][index1]);
}
}
if (temp = valueMerged(values, typeMergedValue, modeValue), temp.error) throw new Error(temp.error);
let value = temp.value;
matrix[index1][n] = value;
}
} else {
if (matrix[index1][index2]===nullValue) throw new Error(`There is no edge between '${index1}' and '${index2}'`);
let indexesIn = [];
for (let i=0; i<n; i++) {
if (matrix[i][index2]!==nullValue) {
indexesIn.push(i);
}
}
let indexesOut = [];
for (let j=0; j<n; j++) {
if (matrix[index1][j]!==nullValue) {
indexesOut.push(j);
}
}
if (indexesIn.length===1 && indexesIn[0]===index1 && indexesOut.length===1 && indexesOut[0]===index2) {
for (let j=0; j<n; j++) {
matrix[index1][j] = matrix[index2][j];
}
for (let i=0; i<n; i++){
matrix[i].splice(index2, 1);
}
matrix.splice(index2, 1);
matrix[index1][index1] = nullValue;
} else {
throw new Error(`Edge between '${index1}' and '${index2}' is not suitable for unsplitting`);
}
}
} catch(e){dev.error = `#Error operateSplittingGraph(): ${clean(e.message)}`}
return dev;
}Operar subdivisión grafo operateSubdivisionGraph
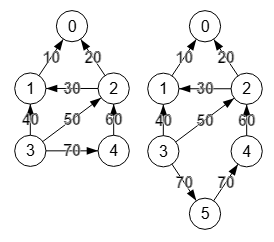
La operación subdivisión de una arista se basa en insertar un nuevo nodo en medio de esa arista.
0 0 0 0 0 10 0 0 0 0 20 30 0 0 0 0 40 50 0 70 0 0 60 0 0
En la Figura tenemos a la izquierda un grafo dirigido ponderado con esta matriz de adyacencia (modo 0/number), aplicando subdivisión a la arista "3🡒4" para obtener el grafo de la derecha, observando el nuevo nodo "5" que se inserta entre los extremos de esa arista.
{"error":"",
"matrix":
[[0,0,0,0,0,0],
[10,0,0,0,0,0],
[20,30,0,0,0,0],
[0,40,50,0,0,70],
[0,0,60,0,0,0],
[0,0,0,0,70,0]]}Este es el resultado obtenido.
En la Figura vemos las opciones para la subdivisión de la arista entre los nodos índice 1 e índice 2. En tipo valor fusionado se contemplan las opciones ninguno, primero, último, mínimo, máximo, suma y media. Con ninguno no se fusionan valores. Con valores primero hasta suma replica el mismo valor existente en la arista "3🡒4" con valor "70" a las nuevas aristas "3🡒5" y "5🡒4". Con valor media se divide ese valor entre dos, así que "3🡒5" y "5🡒4" tendrían valor "35".
La opción posicionar sirve para reubicar los nodos en la posición que tenían antes de ejecutar la operación.
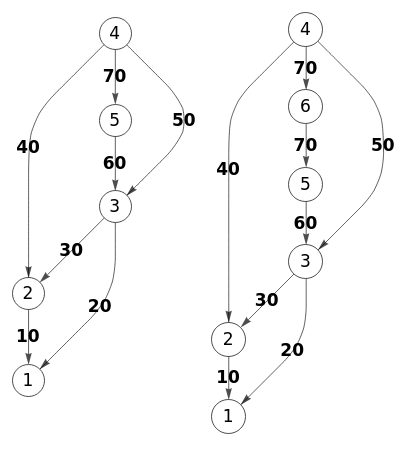
En la Figura exportamos a Wolfram. Como no encuentro una función específica para llevarlo a cabo, componemos el siguiente código usando funciones de Wolfram.
g = WeightedAdjacencyGraph[{{∞,∞,∞,∞,∞},{10,∞,∞,∞,∞},{20,30,∞,∞,∞},{∞,40,50,∞,70},{∞,∞,60,∞,∞}}, ImageSize->188, VertexSize->{"Scaled", 0.08},
VertexLabels->Placed["Index", Center], VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
EdgeLabels->"EdgeWeight", VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
n = Max[VertexList[g]];
v1 = 4;
v2 = 5;
e = DirectedEdge[v1, v2];
w1 = PropertyValue[{g, e}, EdgeWeight];
op = "sum";
w2 = If[op=="mean", w1/2, w1];
w1 = If[op=="mean", w2, w1];
g = EdgeAdd[g, {v1->n+1, n+1->v2}];
g = EdgeDelete[g, e];
Graph[g, EdgeWeight->{DirectedEdge[v1,n+1]->w1, DirectedEdge[n+1,v2]->w2}]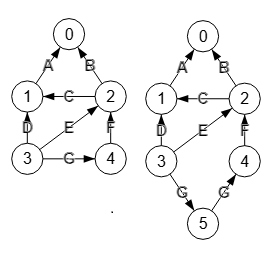
En la Figura vemos a la izquierda el grafo con aristas etiquetadas. Y a la derecha el resultado de la subdivisión de la arista "3🡒4", creándose el nuevo nodo "5" y replicándose el valor "G" en las nuevas aristas "3🡒5" y "5🡒4" usando para valor fusionado cualquiera que no sea "ninguno", pues el resto producirán el mismo resultado.
null null null null null "A" null null null null "B" "C" null null null null "D" "E" null "G" null null "F" null null
Esta es la matriz de adyacencia del grafo inicial en modo null/value.
{"error":"",
"matrix":
[[null,null,null,null,null,null],
["A",null,null,null,null,null],
["B","C",null,null,null,null],
[null,"D","E",null,null,"G"],
[null,null,"F",null,null,null],
[null,null,null,null,"G",null]]}Este es el resultado obtenido.
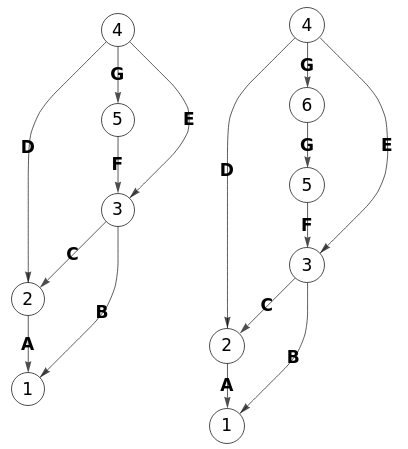
En la Figura vemos el grafo inicial y el resultado de la subdivisión "4🡒5" en Wolfram, equivalente a "3🡒4" de nuestra aplicación. Dado que no encuentro una función específica en Wolfram para hacer esto, es por lo que he compuesto el siguente código con otros recursos de Wolfram.
g = AdjacencyGraph[{{0,0,0,0,0},{1,0,0,0,0},{1,1,0,0,0},{0,1,1,0,1},{0,0,1,0,0}}, ImageSize->188,
VertexSize->{"Scaled", 0.08}, VertexLabels->Placed["Index", Center], VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], EdgeLabels->{(2->1)->"A", (3->1)->"B", (3->2)->"C", (4->2)->"D", (4->3)->"E", (4->5)->"G", (5->3)->"F"},
VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
n = Max[VertexList[g]];
v1 = 4;
v2 = 5;
e = DirectedEdge[v1, v2];
w1 = PropertyValue[{g, e}, EdgeLabels];
op = "sum";
w2 = If[op=="mean", w1/2, w1];
w1 = If[op=="mean", w2, w1];
g = EdgeAdd[g, {v1->n+1, n+1->v2}];
g = EdgeDelete[g, e];
Graph[g, EdgeLabels->{DirectedEdge[v1,n+1]->w1, DirectedEdge[n+1,v2]->w2}]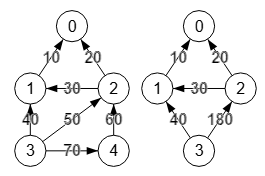
La operación inversa de la subdivisión es el suavizado (smoothing).
0 0 0 0 0 10 0 0 0 0 20 30 0 0 0 0 40 50 0 70 0 0 60 0 0
En la Figura vemos a la izquierda el grafo inicial ponderado (modo 0/number) y a la derecha el resultado del suavizado del nodo "4". Vea que se aplica suavizado al nodo "4" sin que previamente se haya aplicado subdivisión, pues para aplicar suavizado solo es necesario que el nodo tenga una arista entrante y otra saliente. En ese grafo inicial el único nodo que cumple eso es el "4". Aplicando "suma" para tipo valor fusionado vemos que el nodo "4" se elimina y las aristas "3🡒4" con valor "70", "4🡒2" con valor "60" y "3🡒2" con valor "50" se fusionan en una única arista "3🡒2" con valor "70+60+50 = 180". Podíamos haber optado por primero, último, mínimo, máximo y media para ese valor fusionado a partir de la lista de valores "70, 60, 50".
{"error":"",
"matrix":
[[0,0,0,0],
[10,0,0,0],
[20,30,0,0],
[0,40,180,0]]}}Este es el resultado obtenido.
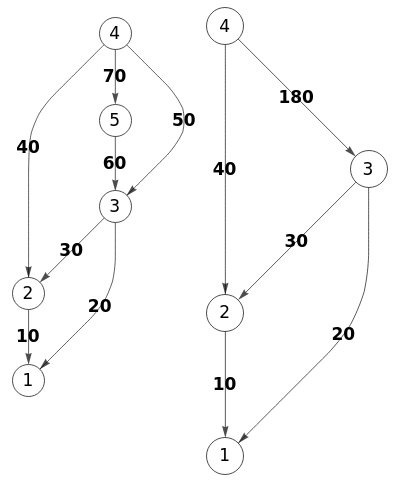
En la Figura vemos el grafo inicial y el resultado obtenido en Wolfram, aplicando otros recursos pues no veo que Wolfram tengan una función específica para el suavizado.
g = WeightedAdjacencyGraph[{{∞,∞,∞,∞,∞},{10,∞,∞,∞,∞},{20,30,∞,∞,∞},{∞,40,50,∞,70},{∞,∞,60,∞,∞}}, ImageSize->188,
VertexSize->{"Scaled", 0.08}, VertexLabels->Placed["Index", Center], VertexLabelStyle->Directive[Black,17.5],
EdgeLabelStyle->Directive[Black,17.5,Bold], EdgeLabels->"EdgeWeight", VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
n = Max[VertexList[g]];
v = 5;
d = DirectedGraphQ[g];
f = EdgeList[g];
l1 = If [d, First[Select[f, Last[#]==v&]], First[Select[f, Last[#]==v&]]];
l2 = If [d, First[Select[f, First[#]==v&]], Last[Select[f, Last[#]==v&]]];
e = DirectedEdge[First[l1], Last[l2]];
m0 = PropertyValue[{g, e}, EdgeWeight];
op = "sum";
m1 = PropertyValue[{g, l1}, EdgeWeight];
m2 = PropertyValue[{g, l2}, EdgeWeight];
m = If[op=="sum", (m1+m2), If[op=="mean", (m1+m2)/2, If[Or[op=="first", op=="min"], m1, If[Or[op=="last", op=="max"], m2, 1]]]];
m = If[EdgeQ[g, e], If[op=="sum", (m+m0), If[op=="mean", (m+m0)/2, If[Or[op=="first", op=="min"], m1, If[Or[op=="last", op=="max"], m2, 1]]]]];
g = EdgeDelete[g, l1];
g = EdgeDelete[g, l2];
g = VertexDelete[g, {v}];
g = If[Not[EdgeQ[g,e]], EdgeAdd[g, {e}], g];
Graph[g, EdgeWeight->{e->m}]A continuación vemos el JavaScript que ejecuta operateSubdivisionGraph() que usa getMatrixModeValue(), isGraphDirected() y valueMerged(). El argumento smoothing nos permite suavizar una arista.
function operateSubdivisionGraph({matrix=[], index1=0, index2=0, typeMergedValue="none", smoothing=false}) {
let dev = {error: "", matrix}, temp;
try {
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
let temp = getMatrixModeValue({matrix});
if (typeof temp==="string") throw new Error (temp);
let [modeValue, nullValue] = temp;
let n = matrix.length;
if (!smoothing) {
if (matrix[index1][index2]===nullValue) throw new Error(`There is no edge between '${index1}' and '${index2}'`);
for (let i=0; i<n; i++) {
matrix[i].push(nullValue);
}
let row = Array.from({length: n+1}, ()=>nullValue);
matrix.push(row);
let value1 = matrix[index1][index2];
if (temp = valueMerged([value1], typeMergedValue, modeValue), temp.error) throw new Error(temp.error);
value1 = temp.value;
let value2 = temp.value;
matrix[index1][n] = value1;
matrix[n][index2] = value2;
matrix[index1][index2] = nullValue;
if (!directed){
matrix[n][index1] = value1;
matrix[index2][n] = value2;
matrix[index2][index1] = nullValue;
}
} else {
let parentsIn = [];
for (let i=0; i<n; i++) {
if (matrix[i][index1]!==nullValue) {
parentsIn.push(i);
}
}
let parentsOut = [];
for (let j=0; j<n; j++) {
if (matrix[index1][j]!==nullValue) {
parentsOut.push(j);
}
}
if (directed && parentsIn.length===1 && parentsOut.length===1 ||
!directed && parentsIn.length===2 && parentsOut.length===2 && parentsIn[0]===parentsOut[0] && parentsIn[1]===parentsOut[1]){
let [i, j] = directed ? [parentsIn[0], parentsOut[0]] : parentsIn;
let value3 = matrix[i][j];
matrix[i][j] = matrix[i][index1];
let value1 = matrix[i][index1];
let value2 = matrix[index1][j];
let values = [value1, value2, value3];
if (!directed) matrix[j][i] = matrix[i][index1];
for (let i=0; i<n; i++) {
matrix[i].splice(index1, 1);
}
matrix.splice(index1, 1);
if (temp = valueMerged(values, typeMergedValue, modeValue), temp.error) throw new Error(temp.error);
matrix[i][j] = temp.value;
} else {
throw new Error(`The node is not suitable for smoothing`);
}
}
} catch(e){dev.error = `#Error operateSubdivisionGraph(): ${clean(e.message)}`}
return dev;
}