18 sep 2025

Circuitos y rastros Eulerianos

Encontrar circuito o rastro Euleriano `findEulerianRoute()`

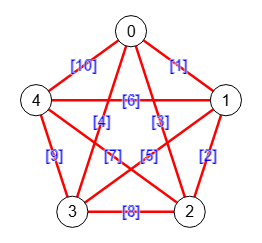
En la sección de acciones de Grafos SVG ejecutamos algoritmos sobre un grafo. Uno de ellos es encontrar una ruta Euleriana en un grafo, que será un camino que debe recorrer todas las aristas del grafo una única vez. En la Figura vemos un ruta Euleriana en el grafo Completo K5 mostrando el circuito 0,1,2,0,3,1,4,2,3,4,0

Un grafo tiene un circuito Euleriano si todos sus vértices tiene grado par. El grafo completo con 5 nodos de la Figura tiene grado 4 en todos sus vértices. El circuito, que en ese ejemplo se inicia en el nodo "0", puede iniciarse en cualquier nodo, como veremos después.

En un tema anterior explicamos las distintas rutas que podemos diferenciar en un grafo, exponiéndose que un circuito (circuit) es una lista de aristas que no se repiten y donde hay más de una repetición de nodos y al menos una es el primero y el último. En este ejemplo vemos que no se repiten las aristas y hay nodos que se repiten, siendo uno de ellos el "0" que se repite al inicio y final.

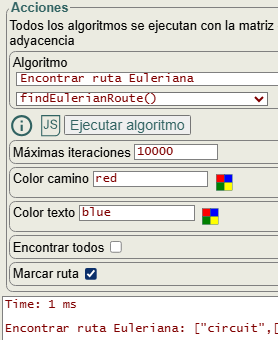
En la Figura vemos la aplicación donde la opción encontrar todos está desactivada, devolviéndose el primer circuito desde el nodo "0". La opcion marcar rutas agrega el número de orden de visita de cada arista entre corchetes, lo que nos permitirá seguir el recorrido de la ruta.

La aplicación actualizará el grafo resaltando la ruta con el color camino y color texto para el etiquetado de las aristas.

Devuelve el resultado en un Array que volcamos en el área de texto inferior obteniéndose ["circuit", [[0,1,2,0,3,1,4,2,3,4,0]], "", 1], con la primera posición devoviendo "none", "circuit" o "trail" en caso de no encontrar ninguno, encontrar un circuito o un rastro. A continuación se muestra la lista de nodos, donde existe una arista entre cada dos nodos. Luego viene una cadena String con un mensaje de advertencia si fuera el caso. Y finalmente un número que cuenta el número de rutas encontradas, una en este caso, pues con la opción encontrar todos que veremos después devolverá varias.

Time: 1 ms

Encontrar ruta Euleriana: ["circuit",[[0,1,2,0,3,1,4,2,3,4,0]],"",1]

Puede usar este JSON para importar el ejemplo:

{"nodes":[
    {"index":0,"nodeOffset":"2.5","parent":[{"index":-1},{"index":4}]},
    {"index":1,"nodeOffset":"65.54 2.64","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"26.01 47.36","parent":[{"index":0},{"index":1}]},
    {"index":3,"nodeOffset":"-46.01 47.36","parent":[{"index":0},{"index":1},{"index":2}]},
    {"index":4,"nodeOffset":"-35.54 -22.36","parent":[{"index":1},{"index":2},{"index":3}]}
],
"config":{
    "algorithm":"Find Eulerian route",
    "markRoute":true
}}

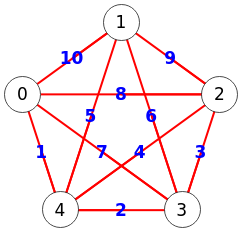
En la Figura vemos la exportación a Wolfram del ejemplo anterior, que usa la función FindEulerianCycle[g, n], siendo "n" el número de ciclos devueltos, si se omite se devuelve el primero encontrato. Wolfram incluye en el nombre de la función el término "ciclo", pero realmente se refiere a circuit o tour que son sinónimos, tal como vemos en Eulerian Cycle de Wolfram MathWorld. Sin embargo no veo que Wolfram contemple buscar un rastro (trail) Euleriano.

No podemos omitir First, pues aunque al no haber especificado "n" en FindEulerianCycle[g, n] se entiende como FindEulerianCycle[g, 1], pero aún así se devuelve como un Array dentro de otro {{1-5, 5-4, 4-3, 3-5, 5-2, 2-4, 4-1, 1-3, 3-2, 2-1}}, así que es necesario extraer el primero y único ciclo. Vea que Wolfram devuelve una lista de aristas, mientras que en nuestra aplicación se devuelve la lista de nodos [[0,1,2,0,3,1,4,2,3,4,0]], que si incrementamos un índice dado que Wolfram simpre los inicia en "1" y lo ponemos como aristas en formato Wolfram sería {{1-2, 2-3, 3-1, 1-4, 4-2, 2-5, 5-3, 3-4, 4-5, 5-0}}, que no coincide con la anterior. Esto es porque en ese grafo existen muchos circuitos, como veremos en otro apartado, de tal forma que si los algoritmos no son iguales el primero que se obtenga no tiene porque ser el mismo en ambos.

g = AdjacencyGraph[{{0,1,1,1,1},{1,0,1,1,1},{1,1,0,1,1},{1,1,1,0,1},{1,1,1,1,0}}, ImageSize->243, 
VertexSize->{"Scaled", 0.13}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center], 4->Placed[3,Center], 
5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold],
VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
a = FindEulerianCycle[g];
e = First[a];
HighlightGraph[g, {Style[EdgeList[e], Red, Thick], Annotation[EdgeList[e], EdgeLabelStyle->Directive[Blue,17.5,Bold]], Table[Labeled[e[[i]], i], {i, Length[e]}]}]

En lo anterior se usa recursos adicionales para resaltar el circuito con HighlightGraph y para etiquetarlo con Table y Labeled.

Marcando encontrar todos buscará cada ruta (circuito) desde cada uno de los 5 nodos del grafo, mostrándose con los botones que se ubican en la parte superior derecha del área del SVG. Se obtiene este resultado, observando que cada ciclo se inicia en uno de los nodos 0, 1, 2, 3 y 4.

Time: 1 ms

Encontrar ruta Euleriana: ["circuit",
[[0,1,2,0,3,1,4,2,3,4,0],
[1,0,2,1,3,0,4,2,3,4,1],
[2,0,1,2,3,0,4,1,3,4,2],
[3,0,1,2,0,4,1,3,2,4,3],
[4,0,1,2,0,3,1,4,2,3,4]],"",5]

En Wolfram no existe este concepto, pues con FindEulerianCycle[g, n] encontrará los primeros "n" ciclos. Si n=5 devolverá los cinco primeros que se inician desde el primer nodo "0". Podemos usar FindEulerianCycle[g, All] usando "All" devolviendo todos los ciclos Eulerianos del grafo, pero esto lo contemplamos aparte con el algoritmo findEulerianRouteAll() que veremos en un siguiente apartado.

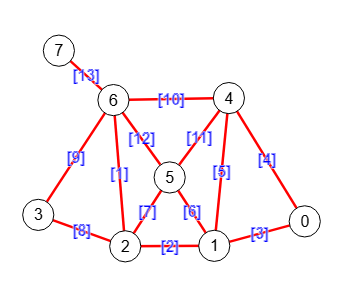
Un grafo con todos los nodos pares menos dos de ellos que son impares tiene un rastro Euleriano. El grafo de la Figura tiene dos nodos impares, el nodo "7" con grado 1 y el "6" con grado 5, el resto tienen grado 2 o 4.

El rastro Euleriano se inicia en alguno de los dos nodos impares y acaba en el otro, recordando que un rastro (trail) es una lista de aristas que no se repiten y donde hay más de una repetición de nodos o si hay solo una no es el primero y el último, pues sería un circuito.

La aplicación devuelve el siguiente resultado, observando la ruta "trail":

Time: 1 ms

Encontrar ruta Euleriana: ["trail",[[6,2,1,0,4,1,5,2,3,6,4,5,6,7]],"",1]

Con este JSON puede importar el ejemplo:

{"nodes":[
    {"index":0,"nodeOffset":"72.13 76.2","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"52.54 61","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"16.87 36.2","parent":[{"index":1}]},
    {"index":3,"nodeOffset":"-18 -1.4","parent":[{"index":2}]},
    {"index":4,"nodeOffset":"25.06 1.8","parent":[{"index":0},{"index":1}]},
    {"index":5,"nodeOffset":"1.33 8.6","parent":[{"index":1},{"index":2},{"index":4}]},
    {"index":6,"nodeOffset":"-21.2 -47.4","parent":[{"index":2},{"index":3},{"index":4},{"index":5}]},
    {"index":7,"nodeOffset":"-26.4 -92.2","parent":[{"index":6}]}
],
"config":{
    "algorithm":"Find Eulerian route",
    "markRoute":true
}}

Como dijimos antes, Wolfram no parece contemplar encontrar un rastro Euleriano. Si exportamos a Wolfram el ejemplo, la función FindEulerianCycle[g] devolverá una lista vacía {}, acusando luego el error First: {} has zero length and no first element con los subsiguientes errores.

Con encontrar todos se obtienen las dos únicas rutas (rastros) que se inician en cada uno de los 2 nodos impares. Vea que el primero se inicia en "6" y acaba en "7" y el segundo es al revés.

Time: 1 ms

Encontrar ruta Euleriana: ["trail",
[[6,2,1,0,4,1,5,2,3,6,4,5,6,7],
[7,6,2,1,0,4,1,5,2,3,6,4,5,6]],"",2]

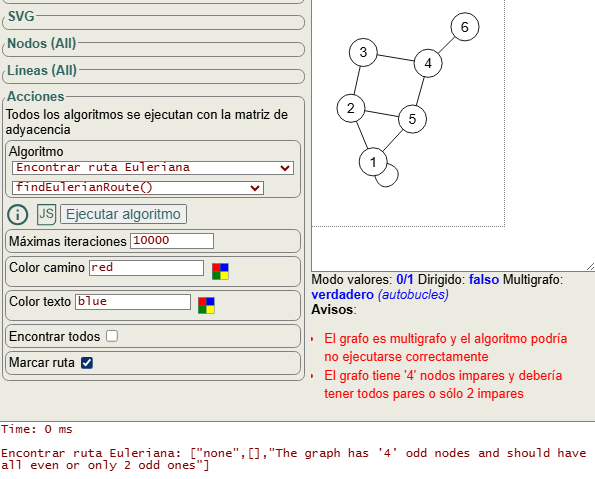
Como se observa en la Figura, la aplicación advierte cuando el grafo es multigrafo, pues dado que todos los algoritmos se ejecutan sobre la matriz de adyacencia y debido a sus limitaciones, es posible que el resultado no sea correcto. En el apartado problema de los puentes de Königsberg que veremos más abajo comentaremos más sobre esto.

Recordando que sólo hay circuito Euleriano si todos los nodos son pares o rastro Euleriano si hay 2 nodos impares y el resto pares, la aplicación informa también de ello. El resultado para el grafo dado es el siguiente:

Time: 0 ms


Encontrar ruta Euleriana: ["none",[],"The graph has '4' odd nodes and should have all even or only 2 odd ones"]

Las frases de advertencia y error en los algoritmos siempre se escriben en inglés y no se traducen en el resultado, pues se trata de ofrecer exactamente lo que el algoritmo devuelve. Puede importar este ejemplo con este JSON:

{"nodes":[
    {"index":0,"nodeOffset":"-22.8 65.2","value":"1","parent":[{"index":-1},{"index":0,"lineType":"cubic","lineOffset":"4 0 0 4"}]},
    {"index":1,"nodeOffset":"-16 16.4","value":"2","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"-27.2 -33.4","value":"3","parent":[{"index":1}]},
    {"index":3,"nodeOffset":"1.6 -53.6","value":"4","parent":[{"index":2}]},
    {"index":4,"nodeOffset":"-22 21.2","value":"5","parent":[{"index":0},{"index":1},{"index":3}]},
    {"index":5,"nodeOffset":"18 -94.8","value":"6","parent":[{"index":3}]}
],
"config":{
    "algorithm":"Find Eulerian route"
}}

Exportando ese ejemplo a Wolfram resulta que FindEulerianCycle[g] devuelve una lista vacía {}, con lo que las siguientes sentencias acusarán errores. Veremos que no advierte que el grafo no tiene circuito Euleriano por los motivos que nuestra aplicación si informa.

En los ejemplos anteriores hemos buscado circuitos y rastros Eulerianos en un grafo no dirigido. También es posible aplicarlo a uno dirigido, pero antes veamos que son los grados de entrada y salida de los nodos de un grafo.

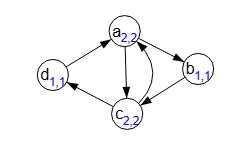
En Figura vemos la ejecución del algoritmo getVertexInOutDegrees({matrix}), exponiendo para cada nodo un subíndice n,m donde "n" son el número de aristas que entran al nodo y "m" son las que salen. Se devuelve un Array con cada pareja de valores para cada nodo correlativamente:

Time: 0 ms

Obtener grados entrada/salida de los vértices: [[2,2],[1,1],[2,2],[1,1]]

Valor nodo → [grado entrada, grado salida] ⇒ 
a → [2,2], b → [1,1], c → [2,2], d → [1,1]

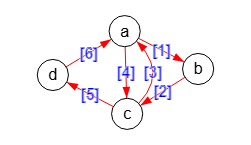
Un grafo dirigido tiene un circuito Euleriano si cada nodo tiene las mismas aristas de entrada y salida. Como vemos en la Figura, esto sucede para el grafo de ejemplo, obteniéndose el circuito Euleriano [0,1,2,0,2,3,0] que vemos en la Figura, o bien con los valores de las aristas ["a","b","c","a","c","d","a"].

Time: 0 ms

Encontrar ruta Euleriana: ["circuit",[[0,1,2,0,2,3,0]],"",1]

Valores de nodos de circuito ⇒ 
["a","b","c","a","c","d","a"]

Con este JSON puede importar el ejemplo.

{"nodes":[
    {"index":0,"nodeOffset":"30","parent":[{"index":-1},{"index":2,"markerStart":"none","markerEnd":"arrow"}]},
    {"index":1,"nodeOffset":"39.47 15.2","parent":[{"index":-1},{"index":0},{"index":2,"markerStart":"none","markerEnd":"arrow"}]},
    {"index":2,"nodeOffset":"-9 33.2","parent":[{"index":-1},{"index":3,"markerStart":"none","markerEnd":"arrow"},{"index":0,"markerStart":"none","markerEnd":"arrow","lineType":"quadratic","lineOffset":3.46}]},
    {"index":3,"nodeOffset":"-58.8 17.6","parent":[{"index":-1},{"index":0,"markerStart":"none","markerEnd":"arrow"}]}
],
"config":{
    "nodeValueAuto":"alphabetic-lower",
    "markerStart":"arrow",  
    "algorithm":"Find Eulerian route",
    "markRoute":true
}}

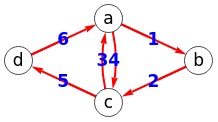
Exportando a Wolfram el ejemplo vemos en la Figura que se obtiene el mismo resultado.

g = AdjacencyGraph[{{0,1,1,0},{0,0,1,0},{1,0,0,1},{1,0,0,0}}, ImageSize->218, VertexSize->{"Scaled", 0.14}, VertexLabels->{1->Placed["a",Center], 2->Placed["b",Center], 3->Placed["c",Center], 4->Placed["d",Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, DirectedEdges->True, EdgeStyle->{{Black,Thickness[0.005]}}];
a = FindEulerianCycle[g];
e = First[a];
HighlightGraph[g, {Style[EdgeList[e], Red, Thick], Annotation[EdgeList[e], EdgeLabelStyle->Directive[Blue,17.5,Bold]], Table[Labeled[e[[i]], i], {i, Length[e]}]}]

Hemos ajustado el tamaño del grafo en Wolfram como se observa en la Figura, factores sobre la unidad para incrementar o reducir tamaños de imagen, vértices, textos y grueso de aristas. Vemos en el código Wolfram que el tamaño de la imagen ImageSize->218 aplicando un factor de 1.5, pues el tamaño inicial de 146 que exportaba la aplicación resultaría en una imagen demasiado pequeña.

Código JavaScript para encontrar una ruta Euleriana `findEulerianRoute()`

El código JavaScript para ejecutar findEulerianRoute() es el siguiente.

function findEulerianRoute({matrix=[], findAll=false}) {
    let result = ["none", [], ""], temp;
    try {
        let connected = isGraphConnected({matrix});
        if (typeof connected==="string") throw new Error(connected);
        if (!connected) {
            result[2] =  `The graph is not connected`;
            result.warnings = [result[2]];
            return result;
        }
        let directed = isGraphDirected({matrix});
        if (typeof directed==="string") throw new Error(directed);
        let odd = [];
        if (directed) {
            let degreesInOut = getVertexInOutDegrees({matrix});
            if (typeof degreesInOut==="string") throw new Error(degreesInOut);
            for (let i=0; i<degreesInOut.length; i++) {
                let deg = degreesInOut[i];
                if (deg[0]!==deg[1]){
                    result[2] = `The graph must have all nodes with the same in/out degrees, the node with index '${i}' has in/out degrees '[${deg.join(",")}]'`;
                    result.warnings = [result[2]];
                    return result;
                }
            }
        } else {
            let degrees = getVertexDegrees({matrix});
            if (typeof degrees==="string") throw new Error(edges);
            for (let i=0; i<degrees.length; i++) {
                if (degrees[i] % 2) odd.push(i);
            }
            if (odd.length>0 && odd.length!==2) {
                result[2] = `The graph has '${odd.length}' odd nodes and should have all even or only 2 odd ones`;
                result.warnings = [result[2]];
                return result;
            }
        }
        let indexes = [];
        let index = -1;
        if (odd.length===0) {
            result[0] = "circuit";
            let n = matrix.length;
            indexes = Array.from({length:n}, (v,i) => i);
        } else {
            result[0] = "trail";
            indexes = odd;
        }
        let [from, to] = findAll ? [0, indexes.length-1] : [0, 0];
        for (let i=from; i<=to; i++) {
            let index = indexes[i];
            let res = [index];
            let matrixCopy = JSON.parse(JSON.stringify(matrix));
            while (!isGraphAllDisconnected({matrix:matrixCopy})) {
                if (iter++, iter>maxIter) return `Maximum iterations '${maxIter}' reached`;
                let neighbors = directed ? getParents({matrix:matrixCopy, index}) : getNeighbors({matrix:matrixCopy, index});
                if (typeof neighbors==="string") throw new Error(neighbors);
                if (neighbors.length===0) {
                    if (isGraphAllDisconnected({matrix:matrixCopy})) result[2] += `Not finished index '${index}'; `;
                    break;
                } else {
                    let j = null;
                    if (neighbors.length>1) {
                        for (let index2 of neighbors) {
                            let bridge = isEdgeBridge({matrix:matrixCopy, edge:[index, index2]});
                            if (typeof bridge==="string") throw new Error(bridge);
                            if  (!bridge) {
                                j = index2;
                                break;
                            }
                        }
                    }
                    if (j===null) j = neighbors[0];
                    matrixCopy[index][j] = 0;
                    if (!directed) matrixCopy[j][index] = 0;
                    index = j;
                    res.push(index);
                }
            }
            result[1].push(res);
        }
        result.push(result[1].length);
        if (result[2]!=="") result.warnings = [result[2]];
    } catch(e){result = e.message}
    return result;
}

El algoritmo tiene dos partes, antes y en el bucle for (let i=from; i<=to; i++). En la primera parte verificamos que el grafo reúne las condiciones para buscar una ruta Euleriana:

Con isGraphConnected({matrix}) vemos si el grafo está desconectado, pues no puede obtenerse una ruta Euleriana en un grafo no conectado.
Con isGraphDirected({matrix}) vemos si el grafo es dirigido o no dirigido, pues:
- Si es dirigido aplicamos getVertexInOutDegrees({matrix}) para comprobar que todos los nodos tienen igual grado de entrada y salida.
- Si es no dirigido aplicamos getVertexDegrees({matrix}) para ver si todos los nodos tienen grado par, con lo que existirá un circuito Euleriano, o al menos hay 2 impares y resto pares, con lo que existirá un rastro Euleriano.

A continuación construimos los límites del rango de búsqueda en las variables from, to para el bucle for (let i=from; i<=to; i++), repitiendo a continuación ese trozo de código:

...
let indexes = [];
let index = -1;
if (odd.length===0) {
    result[0] = "circuit";
    let n = matrix.length;
    indexes = Array.from({length:n}, (v,i) => i);
} else {
    result[0] = "trail";
    indexes = odd;
}
let [from, to] = findAll ? [0, indexes.length-1] : [0, 0];
...

En odd vienen los dos nodos impares en caso de existir, siendo la ruta un "trail", en otro caso será un "circuit". La opción encontrar todos que explicábamos más arriba y que iteraba por todos los nodos del grafo se pasa en el argumento findAll. Si es verdadero se itera por todos los nodos del grafo para el circuito o por los 2 nodos impares para el rastro. En otro caso se inician en el nodo con índice "0".

El bucle externo for (let i=from; i<=to; i++) itera por todos los nodos del grafo o por los dos nodos impares, como hemos dicho. El verdadero bucle que encuentra las rutas es el interno while (!isGraphAllDisconnected({matrix:matrixCopy})), que en forma de pseudo-código hace lo siguiente:

Seleccionar un nodo
Mientras el grafo esté conectado
    Obtener todas las aristas que salen de ese nodo
    Seleccionar una arista que NO SEA PUENTE
    Si no hay ninguna seleccionar la primera
    Agregar esa arista a la ruta Euleriana
    Seleccionar el nodo final de la arista
    Eliminar esa arista en el grafo

Para saber si un grafo tiene todos los nodos desconectados aplicamos isGraphAllDisconnected({matrix}) que veremos en un tema posterior, pues si todas las posiciones de la matriz de adyacencia son valores nulos es que el grafo tiene nodos pero no tiene ninguna arista entre ellos y está, por tanto, totalmente desconectado:

function isGraphAllDisconnected({matrix=[]}){
    let result = false, temp;
    try {
        if (temp = getMatrixModeValue({matrix}), typeof temp==="string") throw new Error (temp);
        let [modeValue, nullValue] = temp;
        result = matrix.flat().every(v => v===nullValue);
    } catch(e){result = e.message}
    return result;
}

Hay que recordar que con getMatrixModeValue() obtenemos el modo valores de la matriz y el valor nulo, pues los modos son "0/1", "0/number", "null/value" y "false/true" siendo los valores nulos 0, 0, null, false respectivamente.

El bucle de selección de nodos está basado en el algoritmo de Fleury, que selecciona aristas que no sean puentes, pues una arista es puente si al eliminarla en el grafo lo hace desconectado (o más desconectado), no habiendo ruta Euleriana en un grafo desconectado como vimos antes. Usa el algoritmo isEdgeBridge({matrix, edge}) que veremos en un tema posterior.

Encontrar todos las rutas Eulerianas `findEulerianRouteAll()`

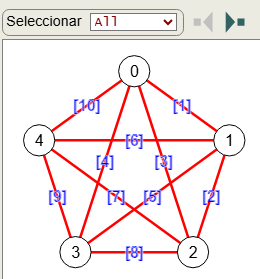
Con el algoritmo findEulerianRouteAll() buscamos todas las rutas Eulerianas posibles en un grafo. En el grafo completo K5 de la Figura vemos que este algoritmo devuelve varias rutas a las que podemos acceder con los botones .

En un grafo completo K5 hay 264 circuitos Eulerianos si no tenemos en cuenta las inversiones de circuitos y tomando todos los ciclos que se inicien en un único nodo.

Estas rutas son circuitos y no rastros para grafos completos con número impar de nodos, pues en un grafo completo con n nodos todos tienen grado n-1 dado que deben conectarse con el resto de nodos, así que para que esos grados sean pares es necesario que n sea impar.

Para grafos completos con número par de nodos todos ellos tendrán grado impar, así que sólo existirá un rastro Euleriano en el grafo completo K2, que tiene únicamente 2 nodos con grado 1. Con este JSON puede importar el grafo:

{"nodes":[
    {"index":0,"nodeOffset":"2.5","parent":[{"index":-1},{"index":4}]},
    {"index":1,"nodeOffset":"65.54 2.64","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"26.01 47.36","parent":[{"index":0},{"index":1}]},
    {"index":3,"nodeOffset":"-46.01 47.36","parent":[{"index":0},{"index":1},{"index":2}]},
    {"index":4,"nodeOffset":"-35.54 -22.36","parent":[{"index":1},{"index":2},{"index":3}]}
],
"config":{
    "algorithm":"Find Eulerian route all",
    "markRoute":true
}}

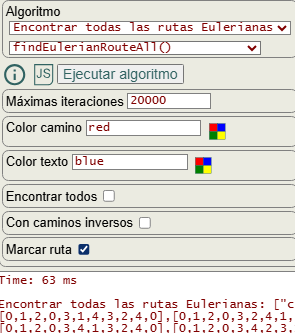
En la Figura vemos la ejecución para encontrar todas las rutas Eulerianas con ese ejemplo, observando las opciones marcar ruta y encontrar todos que ya vimos en el primer apartado para findEulerianRoute(), recordando que con esta última opción activada busca todos los circuitos en un grafo no dirigido tomando como inicio cada nodo del grafo y busca todos los rastros tomando como inicio cada nodo impar de los 2 posibles. Pero hay más rutas posibles y es por eso que tenemos esta función findEulerianRouteAll().

Aparte de usar cada nodo posible como inicio de la ruta, una ruta puede ser [0,1,2,0,3,1,4,2,3,4,0] y su inversa [0,4,3,2,4,1,3,0,2,1,0], optando por incluir las inversas con la opción con caminos inversos.

Vamos a ejecutar el algoritmo con las opciones sin encontrar todos y sin caminos inversos tal como se observa en la Figura, obteniéndose 264 circuitos, omitiendo rutas en el texto con puntos suspensivos para no alargar este página:

Time: 63 ms

Encontrar todas las rutas Eulerianas: ["circuit",[
[0,1,2,0,3,1,4,2,3,4,0],[0,1,2,0,3,1,4,3,2,4,0],[0,1,2,0,3,2,4,1,3,4,0],
[0,1,2,0,3,2,4,3,1,4,0],[0,1,2,0,3,4,1,3,2,4,0],[0,1,2,0,3,4,2,3,1,4,0],
···
[0,3,4,2,0,1,2,3,1,4,0],[0,3,4,2,0,1,3,2,1,4,0],[0,3,4,2,1,0,2,3,1,4,0],
[0,3,4,2,1,3,2,0,1,4,0],[0,3,4,2,3,1,0,2,1,4,0],[0,3,4,2,3,1,2,0,1,4,0]],"",264]

Ejecutando con encontrar todos y sin caminos inversos devolverá 1320 rutas, pues usará como inicio cada uno de los 5 nodos del grafo completo K5, resultando obviamente 5 × 264 = 1320

Time: 89 ms

Encontrar todas las rutas Eulerianas: ["circuit",[
[0,1,2,0,3,1,4,2,3,4,0],[0,1,2,0,3,1,4,3,2,4,0],[0,1,2,0,3,2,4,1,3,4,0],
[0,1,2,0,3,2,4,3,1,4,0],[0,1,2,0,3,4,1,3,2,4,0],[0,1,2,0,3,4,2,3,1,4,0],
···
[4,2,3,1,0,2,1,4,0,3,4],[4,2,3,1,0,4,1,2,0,3,4],[4,2,3,1,2,0,1,4,0,3,4],
[4,2,3,1,2,0,4,1,0,3,4],[4,2,3,1,4,0,1,2,0,3,4],[4,2,3,1,4,0,2,1,0,3,4]],"",1320]

Y por último con encontrar todos y con caminos inversos obtendremos el doble 2640, pues por cada una se incluye también su inverso:

Time: 34 ms

Encontrar todas las rutas Eulerianas: ["circuit",[
[0,1,2,0,3,1,4,2,3,4,0],[0,1,2,0,3,1,4,3,2,4,0],[0,1,2,0,3,2,4,1,3,4,0],
···
[4,3,2,4,1,0,2,1,3,0,4],[4,3,2,4,1,0,3,1,2,0,4],[4,3,2,4,1,2,0,1,3,0,4],
[4,3,2,4,1,2,0,3,1,0,4],[4,3,2,4,1,3,0,1,2,0,4],[4,3,2,4,1,3,0,2,1,0,4]],"",2640]

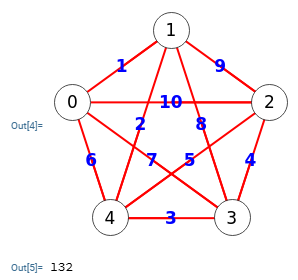
En la Figura vemos el resultado al exportar a Wolfram, donde usamos la función FindEulerianCycle[g, All] para encontrar todos los circuitos. Al final añadimos Length[a] observando que devuelve 132 circuitos, la mitad de los 264 que encontramos nosotros. En el apartado siguiente intentaré saber qué es lo correcto.

g = AdjacencyGraph[{{0,1,1,1,1},{1,0,1,1,1},{1,1,0,1,1},{1,1,1,0,1},{1,1,1,1,0}}, ImageSize->243, VertexSize->{"Scaled", 0.13}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
a = FindEulerianCycle[g, All];
e = First[a];
HighlightGraph[g, {Style[EdgeList[e], Red, Thick], Annotation[EdgeList[e], EdgeLabelStyle->Directive[Blue,17.5,Bold]], Table[Labeled[e[[i]], i], {i, Length[e]}]}]
Length[a]

El código JavaScript para ejecutar findEulerianRouteAll() es el siguiente, donde obviamos la primera parte pues es la misma que la que expusimos en el código de findEulerianRoute(). Dentro del bucle usamos un recursivo para hacer una búsqueda en profundidad recorriendo todas las aristas, sin tener en cuenta si una arista es o no puente como vimos en el primer algoritmo.

function findEulerianRouteAll({matrix=[], findAll=false, withReversePaths=false}) {
    let result = ["none", [], ""];
    try {
        /* Toda esta parte es igual que la que expusimos en el código anterior:
           https://www.wextensible.com/temas/grafos/eulerian.html#t_code1
        */
        for (let i=from; i<=to; i++) {
            let index = indexes[i];
            function recursive(matrix=[], index=0, directed=false, withReversePaths=false, path=[], result=[]) {
                if (iter++, iter>maxIter) {
                    result.warning = `Maximum iterations '${maxIter}' reached`;
                    return result;
                }
                try {
                    path.push(index);
                    if (isGraphAllDisconnected({matrix})) {
                        if (result.length===0 || withReversePaths) {
                            result.push(path);
                        } else {
                            let pathReverse = path.toReversed().toString();
                            if (result.every(v => v.toString()!==pathReverse)){
                                result.push(path);
                            }
                        }
                    } else {
                        let neighbors = directed ? getParents({matrix, index}) : getNeighbors({matrix, index});
                        if (typeof neighbors==="string") throw new Error(neighbors);
                        for (let index2 of neighbors) {
                            let m = JSON.parse(JSON.stringify(matrix));
                            m[index][index2] = 0;
                            if (!directed) m[index2][index] = 0;
                            let res = recursive(m, index2, directed, withReversePaths, [...path], result);
                            if (typeof res==="string") throw new Error(res);
                        }
                    }
                } catch(e){result = e.message}
                return result;
            }
            let res = recursive(matrix, index, directed, withReversePaths);
            if (typeof res==="string") throw new Error(res);
            if (res.hasOwnProperty("warning")) result[2] = res.warning;
            result[1].push(...res);
        }
        result.push(result[1].length)
        if (result[2]!=="") result.warnings = [result[2]];
    } catch(e){result = e.message}
    return result;
}

Cuántos circuitos Eulerianos hay en un grafo completo

Veamos otra vez el código Wolfram que vimos más arriba, que devuelve la ruta como una lista de aristas como se observa en la Figura, usando a = FindEulerianCycle[g, All], que si le quitamos el punto y coma final las mostrará. Devuelve en total 132 circuitos como vimos antes, cuando en nuestra aplicación obteníamos el doble 264.

g = AdjacencyGraph[{{0,1,1,1,1},{1,0,1,1,1},{1,1,0,1,1},{1,1,1,0,1},{1,1,1,1,0}}, ImageSize->243, VertexSize->{"Scaled", 0.13}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center], 4->Placed[3,Center], 5->Placed[4,Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
a = FindEulerianCycle[g, All]
Table[Table[First[j]-1,{j, i}] , {i, a}]
e = First[a];
HighlightGraph[g, {Style[EdgeList[e], Red, Thick], Annotation[EdgeList[e], EdgeLabelStyle->Directive[Blue,17.5,Bold]], Table[Labeled[e[[i]], i], {i, Length[e]}]}]
Length[a]

Intentamos saber cuáles rutas nos faltan para completar las 264 que resulta en nuestra aplicación. Para ello incluimos la sentencia Table[Table[First[j]-1,{j, i}] , {i, a}] para aplicar a las 132 obtenidas en Wolfram para que se inicien en "0", pues los índices en Wolfram se inician en "1" y además cambiar la lista de aristas como una lista de nodos y asi compararlas con las de nuestra aplicación. Obtenemos estas 132 rutas con formato de Wolfram trasladado a nuestro formato, pero aún usando llaves en lugar de corchetes para presentar los Array (abreviamos con puntos suspensivos para no alargarnos):

{{0,1,4,3,2,4,0,3,1,2},{0,1,4,3,2,4,0,2,1,3},{0,1,4,3,2,1,3,0,4,2},{0,1,4,3,2,1,3,0,2,4}
···
{0,1,2,0,3,2,4,3,1,4},{0,1,2,0,3,2,4,1,3,4},{0,1,2,0,3,1,4,3,2,4},{0,1,2,0,3,1,4,2,3,4}}

Preparamos un pequeño código JavaScript para ejecutar en la consola del navegador para encontrar las diferencias entre las 264 de nuestra aplicación y estas 132 de Wolfram (puede descargarlo en formato texto). El resultado de las que faltan en Wolfram son estas 132 rutas, donde sólo presentamos las 12 primeras que empiezan con 0,2,1,0:

[[0,2,1,0,3,1,4,2,3,4,0],[0,2,1,0,3,1,4,3,2,4,0],[0,2,1,0,3,2,4,1,3,4,0],[0,2,1,0,3,2,4,3,1,4,0],
[0,2,1,0,3,4,1,3,2,4,0],[0,2,1,0,3,4,2,3,1,4,0],[0,2,1,0,4,1,3,2,4,3,0],[0,2,1,0,4,1,3,4,2,3,0],
[0,2,1,0,4,2,3,1,4,3,0],[0,2,1,0,4,2,3,4,1,3,0],[0,2,1,0,4,3,1,4,2,3,0],[0,2,1,0,4,3,2,4,1,3,0],
···

Si buscamos todas las rutas de nuestra aplicación que empiecen por 0,2,1,0 encontramos el doble, 24, observando que el segundo grupo son exactamente las que Wolfram no incluye en su búsqueda:

[0,1,2,0,3,1,4,2,3,4,0],[0,1,2,0,3,1,4,3,2,4,0],[0,1,2,0,3,2,4,1,3,4,0],[0,1,2,0,3,2,4,3,1,4,0],
[0,1,2,0,3,4,1,3,2,4,0],[0,1,2,0,3,4,2,3,1,4,0],[0,1,2,0,4,1,3,2,4,3,0],[0,1,2,0,4,1,3,4,2,3,0],
[0,1,2,0,4,2,3,1,4,3,0],[0,1,2,0,4,2,3,4,1,3,0],[0,1,2,0,4,3,1,4,2,3,0],[0,1,2,0,4,3,2,4,1,3,0],
···
[0,2,1,0,3,1,4,2,3,4,0],[0,2,1,0,3,1,4,3,2,4,0],[0,2,1,0,3,2,4,1,3,4,0],[0,2,1,0,3,2,4,3,1,4,0],
[0,2,1,0,3,4,1,3,2,4,0],[0,2,1,0,3,4,2,3,1,4,0],[0,2,1,0,4,1,3,2,4,3,0],[0,2,1,0,4,1,3,4,2,3,0],
[0,2,1,0,4,2,3,1,4,3,0],[0,2,1,0,4,2,3,4,1,3,0],[0,2,1,0,4,3,1,4,2,3,0],[0,2,1,0,4,3,2,4,1,3,0],
···

Y aquí viene la suposición, pues no he podido encontrar más información. Veo que en cada uno de los 264 circuitos del grafo completo K5 que se inician en "0" encontramos 2 subcircuitos, así que por ejemplo con la primera ruta en nuestra aplicación tenemos [0,1,2,0,3,1,4,2,3,4,0] en el primer grupo y [0,2,1,0,3,1,4,2,3,4,0] en el segundo grupo, observando que una tiene el primer subcircuito inverso respecto a la otra. Wolfram solo incluye la primera, ignorando no solo las inversiones del circuito completo (como hacemos nosotros para obtener las 264) sino también las inversiones de los subcircuitos.

¿Y cuál es el número correcto de circuitos Eulerianos en un grafo completo K5? Buscando más información encuentro el documento Counting the Number of Euler Circuits in Complete Graphs de John Dwyer, que hace referencia al documento Asymptotic enumeration of Eulerian circuits in the complete graph de Brendan D. McKay y Robert W. Robinson. Son documentos con contenidos matemáticos no simples para mí y sobre los que no voy a entrar, pues lo que importa es que en ambos podemos ver esta tabla:

n	Número de circuitos
1	0
3	2
5	264
7	1.3 × 10⁸
9	9.1 × 10¹⁷

Nos confirma que un grafo completo K5 tiene 264 circuitos Eulerianos. En el segundo documento de McKay y Robinson (y también en Eulerian Path de Wikipedia) se expone una fórmula para calcularlo:

N = 2^(n+1)/2 √π e^-n²/2+11/12 n^(n-2)(n+1)/2 (1+k)

Realmente la fórmula incluye k = O(n^{-1/2 + ∈}), pero después de varios intentos vemos que aplicando n=5, k=0.022789 obtenemos con Wolfram Alpha exactamente los 264 circuitos Eulerianos como se observa en la Figura.

Es el grafo Euleriano `isEulerianGraph()`

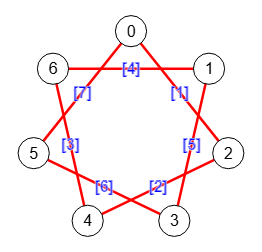
Un grafo es Euleriano si tiene un circuito Euleriano. Por ejemplo, el grafo circulante 7,2 de la Figura es Euleriano. Con la ejecución del algoritmo isEulerianGraph({matrix=[]}) obtenemos el siguiente resultado:

Time: 0 ms

Es el grafo Euleriano: 
[true,[0,2,4,6,1,3,5,0]]

Es un Array con un booleano en primer lugar verificando si es Euleriano y en caso de serlo pasa a continuación el circuito Euleriano. Con este JSON puede importar ese ejemplo:

{"nodes":[
    {"index":0,"nodeOffset":"19.17","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"17.1 15.06","parent":[{"index":-1}]},
    {"index":2,"nodeOffset":"71.5 23.9","parent":[{"index":0}]},
    {"index":3,"nodeOffset":"29.86 51.04","parent":[{"index":1}]},
    {"index":4,"nodeOffset":"-14.86 26.04","parent":[{"index":2}]},
    {"index":5,"nodeOffset":"-46.5 23.9","parent":[{"index":0},{"index":3}]},
    {"index":6,"nodeOffset":"-58.77 -9.94","parent":[{"index":1},{"index":4}]}
],
"config":{
    "algorithm":"Is Eulerian graph"
}}

En Wolfram puede ejecutarse con EulerianGraphQ[g] devolviendo verdadero para el ejemplo anterior. Este es el código Wolfram:

g = AdjacencyGraph[{{0,0,1,0,0,1,0},{0,0,0,1,0,0,1},{1,0,0,0,1,0,0},{0,1,0,0,0,1,0},{0,0,1,0,0,0,1},{1,0,0,1,0,0,0},{0,1,0,0,1,0,0}}, 
ImageSize->253, VertexSize->{"Scaled", 0.12}, VertexLabels->{1->Placed[0,Center], 2->Placed[1,Center], 3->Placed[2,Center], 
4->Placed[3,Center], 5->Placed[4,Center], 6->Placed[5,Center], 7->Placed[6,Center]}, VertexLabelStyle->Directive[Black,17.5], 
EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
EulerianGraphQ[g]

A continuación exponemos el código JavaScript para ejecutar isEulerianGraph() que se basa en findEulerianRoute():

function isEulerianGraph({matrix=[]}){
    let result = [false];
    try {
        let temp = findEulerianRoute({matrix, markRoute:true});
        if (typeof temp==="string") {
            result.push(temp);
        } else {
            result[0] = temp[0]==="circuit";
            if (result[0]) result.push(temp[1][0]);
            if (temp[2]!=="") result.push(temp[2]);
        }
    } catch(e){result = e.message}
    return result;
}

El problema de los puentes de Königsberg

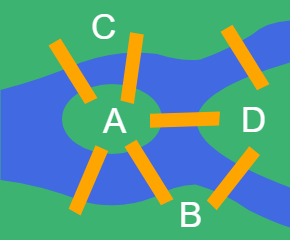
El problema de los puentes de Königsberg se planteaba sobre cómo establecer una ruta sobre el plano que se muestra en la Figura, que representa un rio que se bifurca generando cuatro zonas A, B, C y D, con 7 puentes que conectan esas zonas.

El problema consistía en encontrar una ruta iniciándose en cualquiera de las zonas y visitar el resto cruzando por cada uno de los puentes una única vez para, finalmente, volver a la zona de inicio.

El problema fue resuelto por Euler en 1736 respondiendo que esa ruta no existe, para lo cual esquematizó el plano en un diagrama donde las zonas eran nodos y los puentes constituían aristas. Esto constituyó el inicio de la teoría de grafos.

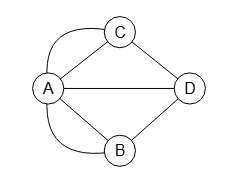
En la Figura vemos el grafo de los puentes de Königsberg, sobre el cual Euler determinó que para que exista tal ruta, todos los nodos deben ser de grado par, pues si llegamos a un nodo (una zona) por una arista (un puente), obligatoriamente debemos salir por otra arista, así que o son pares o no hay forma de conseguir tal ruta. Esta ruta que tratamos de conseguir es el circuito Euleriano que ya hemos visto.

Si dos nodos fueran de grado impar y el resto par podría existir un rastro, pues eligiendo uno de los impares como inicio y el otro como final si que es posible el recorrido. Pero ni siquiera este es el caso, pues todos los 4 nodos son de grado impar.

Este grafo no dirigido es multigrafo con múltiples aristas. Es representable en la aplicación por medio de la estructura JSON, pero las múltiples aristas en un grafo no dirigido no pueden representarse en la matriz de adyacencia, como ya expusimos en un tema anterior sobre las limitaciones de la matriz de adyacencia.

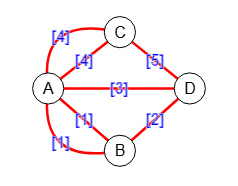
Si ejecutamos el algoritmo para encontrar una ruta Euleriana obtenemos el resultado de la Figura, donde vemos que las aristas múltiples están doblemente marcadas, lo que es un error. La aplicación advierte que El grafo es multigrafo y el algoritmo podría no ejecutarse correctamente. Y este es uno de los casos en que no puede aplicarse ese algoritmo, pues recordamos que todos los algoritmos de la aplicación se ejecutan sobre la matriz de adyacencia, la cual no puede representar esas múltiples aristas.

Con este JSON puede importar ese multigrafo:

{"nodes":[
    {"index":0,"nodeOffset":"-0.7 23","parent":[{"index":-1},{"index":1},{"index":2}]},
    {"index":1,"nodeOffset":"8 48","parent":[{"index":-1},{"index":0,"lineOffset":"-3 3","lineType":"quadratic"}]},
    {"index":2,"nodeOffset":"-12 0.4","parent":[{"index":-1},{"index":0,"lineOffset":"-3 -3","lineType":"quadratic"}]},
    {"index":3,"nodeOffset":"-4 23","parent":[{"index":-1},{"index":2},{"index":0},{"index":1}]}
],
"config":{
    "nodeValueAuto":"alphabetic-upper",
    "algorithm":"Find Eulerian route",
    "findAll":true,
    "markRoute":true
}}

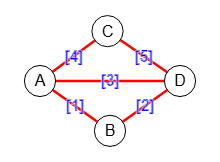
Exportando la matriz de adyacencia del multigrafo anterior e importando esa matriz en la aplicación, tras ponerle los mismos valores a los nodos y reubicarlos, obtenemos el grafo de la Figura, donde vemos que no hay múltiples aristas, pues como dijimos, no es representable en un grafo no dirigido desde la matriz de adyacencia.

Seguimos sin encontrar un circuito, pero si encontramos un rastro (trail) Euleriano, pues hay dos nodos con grado impar (A y D) y el resto son pares. Dos rastros son posibles, iniciándose en cada uno de los dos nodos impares. Este es el resultado obtenido con el algoritmo para encontrar una ruta Euleriana:

Time: 1 ms

Encontrar ruta Euleriana: ["trail",[[0,1,3,0,2,3],[3,0,1,3,2,0]],"",2]

Valores de nodos de rastro ⇒ 
["A","B","D","A","C","D"], ["D","A","B","D","C","A"]

Y con este JSON puede importar ese grafo:

{"nodes":[
    {"index":0,"nodeOffset":"-34 20","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"19 15","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"-7 -25","parent":[{"index":0}]},
    {"index":3,"nodeOffset":"-3 -5","parent":[{"index":0},{"index":1},{"index":2}]}
],
"config":{
    "nodeValueAuto":"alphabetic-upper",
    "algorithm":"Find Eulerian route",
    "findAll":true,
    "markRoute":true
}}

Encontrar circuito o rastro Euleriano findEulerianRoute()

Código JavaScript para encontrar una ruta Euleriana findEulerianRoute()

Encontrar todos las rutas Eulerianas findEulerianRouteAll()