Corte de vértices en un grafo
Encontrar corte mínimo de vértices s-t findSTVertexCut() en grafo dirigido
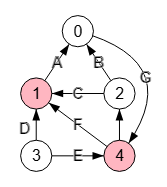
Un corte mínimo de vértices s-t supone encontrar un conjunto mínimo de vértices que separe los nodos "s" y "t" en distintos componentes conectados.
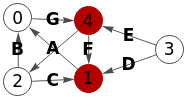
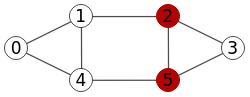
Encontrar corte vértices s-t: [1,4]
En la Figura tenemos un grafo dirigido no ponderado pero con aristas etiquetadas, lo que equivale a decir que todas las aristas tienen peso unitario. El corte de vértices entre nodos "3" y "0" nos devuelve la lista de nodos [1, 4].
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4,"value":"G","lineOffset":"6 -2","lineType":"quadratic"}]},
{"index":1,"parent":[{"index":0,"value":"A"}]},
{"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"C"}]},
{"index":3,"parent":[{"index":1,"value":"D","lineTextOffset":"-0.75 0.25"},{"index":4,"value":"E"}]},
{"index":4,"parent":[{"index":1,"value":"F"},{"index":2}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find s-t vertex cut",
"firstIndex":3
}}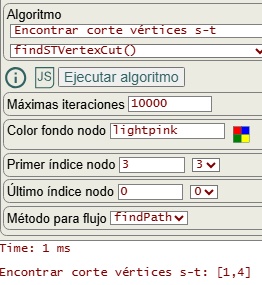
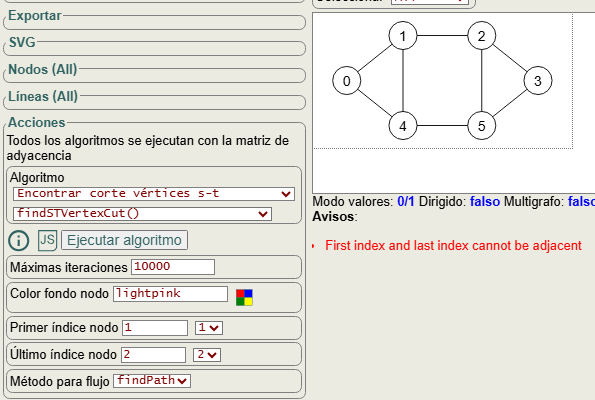
En la Figura vemos las opciones para encontrar el corte mínimo s-t de vértices, con "s" en primer índice nodo y "t" en último índice nodo. El método para flujo puede ser "findPath", "dijkstra" o "floyd". La opción color fondo nodo no se pasa al algoritmo findSTVertexCut(), pues sirve para resaltar los nodos que forman el resultado obtenido con el algoritmo tras su ejecución.
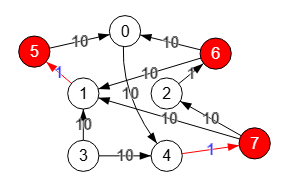
Para encontrar un corte mínimo s-t de vértices usamos el algoritmo findSTEdgeCut() que encuentra el corte mínimo s-t de aristas que vimos en el tema anterior, pero antes tenemos que modificar el grafo como veremos a continuación.
[[0,0,0,0,10,0,0,0], [0,0,0,0,0,1,0,0], [0,0,0,0,0,0,1,0], [0,10,0,0,10,0,0,0], [0,0,0,0,0,0,0,1], [10,0,0,0,0,0,0,0], [10,10,0,0,0,0,0,0], [0,10,10,0,0,0,0,0]]
Lo primero que hacemos es dividir (splitting) todos los nodos del grafo inicial de la Figura a excepción de "s=3" y "t=0", obteniendo el grafo de la Figura. Reubicamos los nuevos nodos "5", "6" y "7" que dividen las nodos "1", "2" y "4" respectivamente para observar mejor este grafo con división de nodos que podemos denominar grafo dividido.
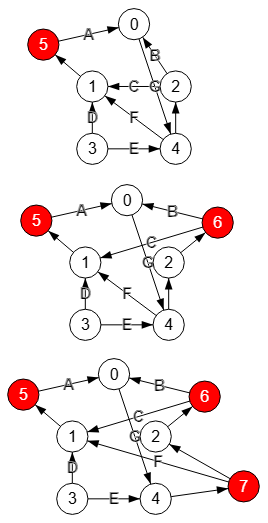
Recordar que la operación operateSplittingGraph() que divide un nodo supone identificar las aristas entrantes y salientes del nodo, con lo que las entrantes permanecen en el mismo nodo y las salientes se traspasan a un nuevo nodo, creando una arista que va desde el nodo que se divide al nuevo nodo. Veamos como operamos la división de los nodos "1", "2" y "4" en ese orden como se observa en Figura.
En la división del nodo "1" tenemos las aristas entrantes "3🡒1, 4🡒1, 2🡒1" que permanecen sin modificación. Y la única saliente "1🡒0" va ahora hasta un nuevo nodo "5" pasando a ser "1🡒5" y luego otra nueva "5🡒0".
El siguiente nodo a dividir es el "2" con arista entrante "4🡒2" que permanece y salientes "2🡒0" y "2🡒1" que tras crear el nuevo nodo "6" pasan a ser "2🡒6" y luego "6🡒1" y "6🡒0".
Por último se divide el nodo "4" con aristas entrantes "3🡒4" y "0🡒4" que permanecen, creándose el nuevo nodo "7" al que se traspasan las salientes "7🡒1" y "7🡒2" y se crea la nueva arista "4🡒7".
Para un grafo no ponderado como este ejemplo, todas las aristas de los nodos que se dividen con dirección a los nuevos nodos, es decir, "1🡒5", "2🡒6" y "4🡒7" se les asigna peso unitario. Y al resto de aristas se les asigna un peso suficientemente grande (10 en este ejemplo y cuyo motivo explicaremos después) para que no intervengan en el resultado del algoritmo para encontrar el máximo flujo entre nodos "3" y "0", pues vamos a usar ese algoritmo desde encontrar corte mínimo aristas s-t para encontrar los aristas de corte y de ahí deducir los vértices de corte.
Encontrar corte aristas s-t: [[1,5],[4,7]]
Aplicando el algoritmo findSTEdgeCut() para encontrar el corte mínimo s-t de aristas en el grafo dividido de la Figura obtendremos las aristas "1🡒5" y "4🡒7", de tal forma que las últimas posiciones "5" y "7" son los nuevos nodos de la división y las primeras posiciones son los nodos "1" y "4" que conforma los vértices mínimos de corte entre nodos "s=3" y "t=0".
El algoritmo findSTVertexCut() lleva a cabo la división de nodos y luego aplica findSTEdgeCut() devolviendo los vértices "1" y "4" que vemos en el resultado del grafo de la Figura. En cualquier caso puede probar la ejecución sobre las aristas del grafo dividido de la Figura con el siguiente JSON:
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4,"value":10,"lineType":"quadratic","lineOffset":-2}]},
{"index":1,"nodeOffset":"0 -25","parent":[{"index":5,"value":1,"lineFontColor":"red"}]},
{"index":2,"nodeOffset":"0 -25","parent":[{"index":6,"value":1,"lineFontColor":"red"}]},
{"index":3,"nodeOffset":"0 -25","parent":[{"index":1,"value":10},{"index":4,"value":10}]},
{"index":4,"nodeOffset":"16.67 -50","parent":[{"index":7,"value":1,"lineFontColor":"red"}]},
{"index":5,"nodeOffset":"-19.6 -16.8","nodeColor":"red","nodeFontColor":"white","parent":[{"index":0,"value":10}]},
{"index":6,"nodeOffset":"19.6 -16","nodeFontColor":"white","nodeColor":"red","parent":[{"index":0,"value":10},{"index":1,"value":10}]},
{"index":7,"nodeOffset":"35.2 -30","nodeColor":"red","nodeFontColor":"white","parent":[{"index":1,"value":10},{"index":2,"value":10}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find s-t edge cut",
"firstIndex":3
}}
Vemos el mismo resultado en Wolfram, que aplica la función FindVertexCut[g, s, t].
g = WeightedAdjacencyGraph[{{∞,∞,∞,∞,1},{1,∞,∞,∞,∞},{1,1,∞,∞,∞},{∞,1,∞,∞,1},{∞,1,1,∞,∞}}, ImageSize -> 188,
VertexSize -> {"Scaled", 0.17}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center],
4 -> Placed[3,Center], 5 -> Placed[4,Center]}, VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold],
EdgeLabels -> {(1->5)->"G", (2->1)->"A", (3->1)->"B", (3->2)->"C", (4->2)->"D", (4->5)->"E", (5->2)->"F"},
VertexStyle -> White, DirectedEdges -> True, EdgeStyle -> {{Black,Thickness[0.005]}}];
v = FindVertexCut[g, 4, 1];
HighlightGraph[g, v]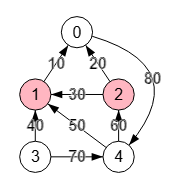
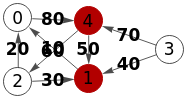
En la Figura vemos el corte mínimo s-t de vértices para el mismo grafo del ejemplo anterior pero ahora con números en las aristas que lo convierte en un grafo ponderado. Vemos que encontramos el corte de vértices "1, 2" cuando antes con el mismo grafo no ponderado encontrábamos el corte "1, 4".
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4,"lineType":"quadratic","lineOffset":"7 -2","value":80}]},
{"index":1,"parent":[{"index":0,"value":10}]},
{"index":2,"parent":[{"index":0,"value":20},{"index":1,"value":30}]},
{"index":3,"parent":[{"index":1,"value":40},{"index":4,"value":70}]},
{"index":4,"parent":[{"index":1,"value":50},{"index":2,"value":60}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find s-t vertex cut",
"firstIndex":3
}}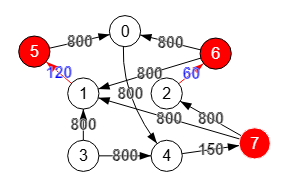
El grafo dividido se observa en la Figura, que se puede importar con la matriz dividida siguiente y una reubicación y estilo de nuevos nodos con el JSON más abajo.
[[0,0,0,0,800,0,0,0], [0,0,0,0,0,120,0,0], [0,0,0,0,0,0,60,0], [0,800,0,0,800,0,0,0], [0,0,0,0,0,0,0,150], [800,0,0,0,0,0,0,0], [800,800,0,0,0,0,0,0], [0,800,800,0,0,0,0,0]]
Se observa que las aristas que van desde los nodos que se dividen a nuevos nodos tiene un valor menor de 800 y el resto tienen ese valor. Por ejemplo, en la división del nodo "1" tenemos las aristas entrantes "3🡒1" con valor 40, "4🡒1" con valor 50 y "2🡒1" con valor 30, por lo que se adjudica a la nueva arista "1🡒5" la suma de pesos entrantes 40+50+30 = 120. Así la capacidad entrante 40+50+30 al nodo "1" en el grafo sin dividir se mantiene en la saliente "1🡒5" con valor 120 en el grafo dividido.
De igual forma vemos las aristas "2🡒6" con valor 60 que es suma de la única entrante "4🡒6" con ese valor. Y "4🡒7" con valor 150 que es suma de "3🡒4" con valor 70 más "0🡒4" con valor 80. Estos valores se aplican con la operación operateSplittingGraph() pasando el argumento typeMergedValue con valor "sum" para que sume los pesos de las aristas entrantes. Puede ver más sobre esta operación con un ejemplo de grafo ponderado en el tema operateSplittingGraph().
Encontrar corte aristas s-t: [[1, 5], [2, 6]]
Aplicando findSTEdgeCut() al grafo dividido de la Figura obtenemos el corte de aristas "1🡒5" y "2🡒6" constituyendo los nodos "1" y "2" como vértices de corte mínimo entre "s=3" y "t=0". Observe que la suma de este corte es 120+60 = 180 menor que el corte de "1" y "4" que suma 120+150 = 270
El valor máximo 800 que se aplica al resto de aristas proviene del cálculo (n × (n-1) / 2) × m siendo "m" el mayor peso de todas las aristas. Como n=5 y m=80 obtenemos el valor máximo (5 × (5-1) / 2) × 80 = 800. Se basa en que para un grafo con "n" nodos el número máximo de aristas para un grafo dirigido y sin bucles es n × (n-1) / 2 con lo que sumando todas esas aristas con el valor de la arista con máximo peso tendremos un valor que nunca podrá superarse en el grafo.
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4,"value":800,"lineType":"quadratic","lineOffset":-2}]},
{"index":1,"nodeOffset":"0 -25","parent":[{"index":5,"value":120}]},
{"index":2,"nodeOffset":"0 -25","parent":[{"index":6,"value":60}]},
{"index":3,"nodeOffset":"0 -25","parent":[{"index":1,"value":800},{"index":4,"value":800}]},
{"index":4,"nodeOffset":"16.67 -50","parent":[{"index":7,"value":150}]},
{"index":5,"nodeOffset":"-19.6 -16.8","nodeColor":"red","nodeFontColor":"white","parent":[{"index":0,"value":800}]},
{"index":6,"nodeOffset":"19.6 -16","nodeColor":"red","nodeFontColor":"white","parent":[{"index":0,"value":800},{"index":1,"value":800}]},
{"index":7,"nodeOffset":"35.2 -30","nodeBorderColor":"white","nodeColor":"red","nodeFontColor":"white","parent":[{"index":1,"value":800},{"index":2,"value":800}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find s-t edge cut",
"firstIndex":3
}}
Vemos que Wolfram parece ignorar el corte de vértices en un grafo ponderado, pues el resultado que alcanza es el mismo que vimos para el no ponderado. En la documentación de la función FindVertexCut[g, s, t] no expone nada acerca de la aplicación sobre grafos ponderados, cuando en FindEdgeCut dice literalmente For weighted graphs, FindEdgeCut gives an edge cut with the smallest sum of edge weights
que se traduce como Para grafos ponderados, FindEdgeCut da un corte de aristas con la menor suma de pesos
. Sobre esto mantengo cierta duda de que lo que hacemos en la aplicación para el corte de vértices es correcto o bien debemos ignorar los pesos de las aristas tal como lo hace Wolfram.
g = WeightedAdjacencyGraph[{{∞,∞,∞,∞,80},{10,∞,∞,∞,∞},{20,30,∞,∞,∞},{∞,40,∞,∞,70},{∞,50,60,∞,∞}}, ImageSize -> 188,
VertexSize -> {"Scaled", 0.17}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center],
4 -> Placed[3,Center], 5 -> Placed[4,Center]}, VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold],
EdgeLabels -> {(1->5)->80, (2->1)->10, (3->1)->20, (3->2)->30, (4->2)->40, (4->5)->70, (5->2)->50, (5->3)->60},
VertexStyle -> White, DirectedEdges -> True, EdgeStyle -> {{Black,Thickness[0.005]}}];
v = FindVertexCut[g, 4, 1];
HighlightGraph[g, v]Encontrar corte mínimo de vértices s-t findSTVertexCut() en grafo no dirigido
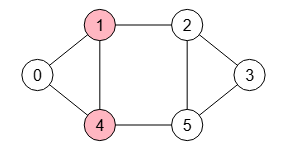
Para encontrar el corte mínimo de vértices entre nodos "s" y "t" en un grafo no dirigido debemos primero convertirlo en dirigido, pues hemos de dividir (splitting) todos los nodos a excepción de "s" y "t" y la operación sólo puede aplicarse a grafos dirigidos, pues se debe identificar las aristas entrantes y salientes de cada nodo.
En el grafo de la Figura vemos que encuentra el corte mínimo de vértices "1, 4" que separa "s=0" y "t=3" en dos componentes, que nos servirá para explicar este apartado. Puede importarlo con el siguiente JSON:
{"nodes":[
{"index":0,"nodeOffset":"-35 17.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"6.67 -27.5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"25 -52.5","parent":[{"index":1}]},
{"index":3,"nodeOffset":"66.67 -57.5","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-26.67 12.5","parent":[{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"8.33 -37.5","parent":[{"index":2},{"index":3},{"index":4}]}
],
"config":{
"algorithm":"Find s-t vertex cut",
"lastIndex":3
}}
0 1 0 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 0 1 0 0 1 1 1 0 0 0 1 0 0 1 1 1 0
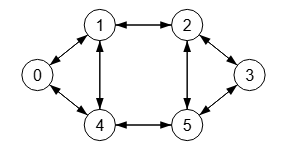
Esta es la matriz de adyacencia del grafo no dirigido de la Figura, matriz simétrica respecto a la diagonal derecha con lo que se identifica en la aplicación como un grafo no dirigido. Como ya hemos dicho otras veces, no es posible representar en la matriz de adyacencia un grafo todo dirigido, pues su matriz es igual que la del grafo no dirigido. Y la aplicación cuando trabaja con matrices de adyacencia opta por considerar una matriz simétrica como la de un grafo no dirigido. Es representable si la aplicación trabaja con el JSON en lugar de la matriz de adyacencia, como vemos en la Figura.
Recordemos además que vamos a aplicar findSTEdgeCut() que a su vez se apoya en findMaximumFlow(), algoritmo que por definición sólo debe aplicarse a grafos dirigidos, pero que también funciona con no dirigidos como explicamos en el tema encontrar máximo flujo en grafos no dirigidos.
Pero antes de aplicar esos algoritmos ahora necesitamos dividir todos los nodos a excepción de "s" y "t" tal como hicimos en el apartado anterior para grafos dirigidos, lo que obliga a convertir un grafo no dirigido en dirigido, pues esta operación división (splitting) debe identificar las aristas entrantes y salientes de los nodos para lo cual el grafo debe ser necesariamente dirigido.
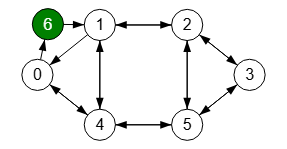
En el tema de la operación que actúa sobre la direccionalidad vimos como convertir un grafo no dirigido en dirigido por medio del uso de la operación subdivisión de un arista.
0 0 0 0 1 0 1 1 0 1 0 1 0 0 0 1 0 1 0 1 0 0 0 1 0 0 1 0 1 1 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0
En la Figura subdividimos la primera arista que encontremos en el grafo, "0🡒1" en este caso, creando el nuevo nodo "6" y las aristas "0🡒6" y "6🡒1". Como se observa en la matriz de adyacencia, ya no es simétrica y por tanto representa a un grafo dirigido. Esta subdivisión de la arista no afecta al algoritmo para encontrar el máximo flujo, pues lo único que tenemos que respetar es que la capacidad de la arista "0🡒1" sea igual que la de las nuevas aristas "0🡒6" y "6🡒1". Como el grafo no es ponderado, la arista "0🡒1" tiene capacidad unitaria al igual que las dos nuevas creadas. En otro caso si la arista inicial tuviese un peso determinado, se trasladará a las nuevas aristas.
{"nodes":[
{"index":0,"nodeOffset":"-5 17.5","parent":[{"index":-1},{"index":4},{"index":6}]},
{"index":1,"nodeOffset":"6.67 -27.5","parent":[{"index":0},{"index":2},{"index":4}]},
{"index":2,"nodeOffset":"35 -2.5","parent":[{"index":1},{"index":3},{"index":5}]},
{"index":3,"nodeOffset":"40 17.5","parent":[{"index":2},{"index":5}]},
{"index":4,"nodeOffset":"-26.67 12.5","parent":[{"index":0},{"index":1},{"index":5}]},
{"index":5,"nodeOffset":"-5 37.5","parent":[{"index":2},{"index":3},{"index":4}]},
{"index":6,"nodeOffset":"-30.8 -52.8","nodeColor":"green","nodeFontColor":"white","parent":[{"index":1}]}
],
"config":{
"markerEnd":"arrow"
}}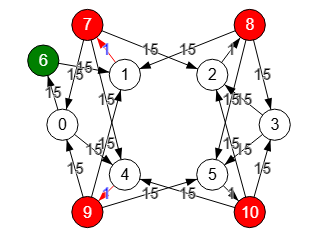
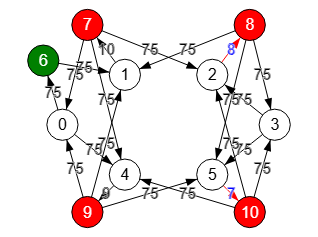
Ahora con el grafo dirigido de la Figura vamos al siguiente paso que es dividir (splitting) todos los nodos "1,2,4,5" a excepción de "s=0" y "t=3", creándose los nuevos nodos "7,8,9,10".
0 0 0 0 15 0 15 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 15 0 0 15 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 15 0 0 0 0 0 0 0 0 0 15 0 15 0 15 0 0 0 0 0 0 0 15 0 15 0 15 0 0 0 0 0 15 15 0 0 0 15 0 0 0 0 0 0 0 15 15 15 0 0 0 0 0 0
A las nuevas aristas "1🡒7", "2🡒8", "4🡒9" y "5🡒10" procedentes de la división de los nodos "1,2,4,5" les aplicamos valor unitario y al resto el valor máximo, que tal como explicamos en el apartado anterior, tiene para este grafo un valor 15, pues es el resultado de n(n-1)/2 × m = 6(6-1)/2 × 1 = 15 dado que todas las aristas del grafo inicial tienen peso unitario y entonces m=1
Encontrar corte aristas s-t: [[1,7],[4,9]]
Aplicando el algoritmo findSTEdgeCut() a este grafo encontramos el corte mínimo de aristas "1🡒7" y "4🡒9", de donde se deduce que el corte mínimo de vértices son los nodos "1" y "4".
{"nodes":[
{"index":0,"nodeOffset":"-25 37.5","parent":[{"index":-1},{"index":4,"value":15},{"index":6,"value":15}]},
{"index":1,"nodeOffset":"30 -32.5","parent":[{"index":7,"value":1}]},
{"index":2,"nodeOffset":"45 -32.5","parent":[{"index":8,"value":1}]},
{"index":3,"nodeOffset":"85 12.5","parent":[{"index":2,"value":15},{"index":5,"value":15}]},
{"index":4,"nodeOffset":"-10 7.5","parent":[{"index":9,"value":1}]},
{"index":5,"nodeOffset":"5 7.5","parent":[{"index":10,"value":1}]},
{"index":6,"nodeOffset":"-16 -63.2","nodeColor":"green","nodeFontColor":"white","parent":[{"index":1,"value":15}]},
{"index":7,"nodeOffset":"-15 -27.5","nodeColor":"red","nodeFontColor":"white","parent":[{"index":0,"value":15},{"index":2,"value":15},{"index":4,"value":15}]},
{"index":8,"nodeOffset":"33.33 -77.5","nodeColor":"red","nodeFontColor":"white","parent":[{"index":1,"value":15},{"index":3,"value":15},{"index":5,"value":15}]},
{"index":9,"nodeOffset":"-40 47.5","nodeColor":"red","nodeFontColor":"white","parent":[{"index":0,"value":15},{"index":1,"value":15},{"index":5,"value":15}]},
{"index":10,"nodeOffset":"50 -52.5","nodeColor":"red","nodeFontColor":"white","parent":[{"index":2,"value":15},{"index":3,"value":15},{"index":4,"value":15}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find s-t edge cut",
"lastIndex":3
}}
En la Figura vemos como Wolfram ejecuta el corte mínimo de vértices con el resultado "2,5" en lugar de "1,4". Para nuestra aplicación el corte "1,4" separa "s=0" y "t=3" mientras que el corte "2,5" separa la pareja contraria "s=3" y "t=0", algo que se puede comprobar en la aplicación.
Wolfram usa FindVertexCut[g, 1, 4] para obtener el corte "3,6" ("2,5" en base 0) mientras que si pasamos FindVerteCut[g, 4, 1] obtenemos el corte "2,5" ("1,4" en base 0). Recuerde que en Wolfram los índices se inician en 1 y en nuestra aplicación en 0.
g = AdjacencyGraph[{{0,1,0,0,1,0},{1,0,1,0,1,0},{0,1,0,1,0,1},{0,0,1,0,0,1},{1,1,0,0,0,1},{0,0,1,1,1,0}},
ImageSize -> 250, VertexSize -> {"Scaled", 0.1}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center],
3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center], 6 -> Placed[5,Center]},
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White,
EdgeStyle -> {{Black,Thickness[0.005]}}];
v = FindVertexCut[g, 1, 4];
HighlightGraph[g, v]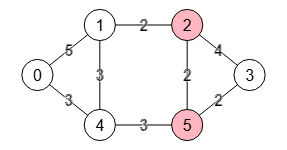
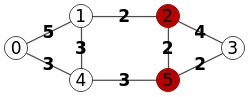
En la Figura vemos el corte mínimo de vértices entre "s=0" y "t=3" para el mismo grafo no dirigido del ejemplo anterior pero ahora con pesos en las aristas. Observamos que el corte de vértices ahora es "2,5" cuando antes sin pesos era "1,4".
{"nodes":[
{"index":0,"nodeOffset":"-35 17.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"6.67 -27.5","parent":[{"index":0,"value":5}]},
{"index":2,"nodeOffset":"25 -52.5","parent":[{"index":1,"value":2}]},
{"index":3,"nodeOffset":"66.67 -57.5","parent":[{"index":2,"value":4}]},
{"index":4,"nodeOffset":"-26.67 12.5","parent":[{"index":0,"value":3},{"index":1,"value":3}]},
{"index":5,"nodeOffset":"8.33 -37.5","parent":[{"index":2,"value":2},{"index":3,"value":2},{"index":4,"value":3}]}
],
"config":{
"algorithm":"Find s-t vertex cut",
"lastIndex":3
}}
En la Figura vemos la conversión de no dirigido a dirigido, creándose el nuevo nodo "6" y las aristas "0🡒6" y "6🡒1" ambas con el mismo peso 5 que la original antes de subdividir la arista "0🡒1".
{"nodes":[
{"index":0,"nodeOffset":"-5 27.5","parent":[{"index":-1},{"index":4,"value":3},{"index":6,"value":5}]},
{"index":1,"nodeOffset":"6.67 -17.5","parent":[{"index":0,"value":5},{"index":2,"value":2},{"index":4,"value":3}]},
{"index":2,"nodeOffset":"35 7.5","parent":[{"index":1,"value":2},{"index":3,"value":4},{"index":5,"value":2}]},
{"index":3,"nodeOffset":"40 27.5","parent":[{"index":2,"value":4},{"index":5,"value":2}]},
{"index":4,"nodeOffset":"-26.67 22.5","parent":[{"index":0,"value":3},{"index":1,"value":3},{"index":5,"value":3}]},
{"index":5,"nodeOffset":"-5 47.5","parent":[{"index":2,"value":2},{"index":3,"value":2},{"index":4,"value":3}]},
{"index":6,"nodeOffset":"-39.6 -52.4","nodeColor":"green","nodeFontColor":"white","parent":[{"index":1,"value":5}]}
],
"config":{
"markerEnd":"arrow"
}}
Y en la Figura vemos el grafo con los nodos "1,2,4,5" divididos y la ejecución del algoritmo findSTEdgeCut() que devuelve las aristas de corte "2🡒8" y "5🡒10", de donde se deduce que el corte mínimo de vértices son los nodos "2" y "5".
Vea que la suma de los pesos de las aristas "2🡒8" y "5🡒10" es 8+7=15 menor que la suma de "1🡒7" y "4🡒9" que es 10+9=19.
Recordemos que el peso máximo 75 se obtiene con la fórmula (n × (n-1) / 2) × m = (6 × (6-1) / 2) × 5 = 75, con n=6 el total de nodos del grafo inicial y m=5 el mayor peso de todas las aristas.
{"nodes":[
{"index":0,"nodeOffset":"-25 37.5","parent":[{"index":-1},{"index":4,"value":75},{"index":6,"value":75}]},
{"index":1,"nodeOffset":"30 -32.5","parent":[{"index":7,"value":10}]},
{"index":2,"nodeOffset":"45 -32.5","parent":[{"index":8,"value":8}]},
{"index":3,"nodeOffset":"85 12.5","parent":[{"index":2,"value":75},{"index":5,"value":75}]},
{"index":4,"nodeOffset":"-10 7.5","parent":[{"index":9,"value":9}]},
{"index":5,"nodeOffset":"5 7.5","parent":[{"index":10,"value":7}]},
{"index":6,"nodeOffset":"-16 -63.2","nodeColor":"green","nodeFontColor":"white","parent":[{"index":1,"value":75}]},
{"index":7,"nodeOffset":"-15 -27.5","nodeColor":"red","nodeFontColor":"white","parent":[{"index":0,"value":75},{"index":2,"value":75},{"index":4,"value":75}]},
{"index":8,"nodeOffset":"33.33 -77.5","nodeColor":"red","nodeFontColor":"white","parent":[{"index":1,"value":75},{"index":3,"value":75},{"index":5,"value":75}]},
{"index":9,"nodeOffset":"-40 47.5","nodeColor":"red","nodeFontColor":"white","parent":[{"index":0,"value":75},{"index":1,"value":75},{"index":5,"value":75}]},
{"index":10,"nodeOffset":"50 -52.5","nodeColor":"red","nodeFontColor":"white","parent":[{"index":2,"value":75},{"index":3,"value":75},{"index":4,"value":75}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find s-t edge cut",
"lastIndex":3
}}
En Wolfram para este grafo ponderado vuelve a encontrar el mismo corte de vértices "2,5" que para el ejemplo no ponderado. Aunque ahora coincide con nuestro resultado, recordar que ya habíamos dicho que Wolfram parece ignorar los pesos al aplicar FindVertexCut[g, s, t].
g = WeightedAdjacencyGraph[{{∞,5,∞,∞,3,∞},{5,∞,2,∞,3,∞},{∞,2,∞,4,∞,2},{∞,∞,4,∞,∞,2},{3,3,∞,∞,∞,3},{∞,∞,2,2,3,∞}},
ImageSize -> 250, VertexSize -> {"Scaled", 0.1}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center],
3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center], 6 -> Placed[5,Center]}, VertexLabelStyle -> Directive[Black,17.5],
EdgeLabelStyle -> Directive[Black,17.5,Bold], EdgeLabels -> {(2->1)->5, (3->2)->2, (4->3)->4, (5->1)->3, (5->2)->3, (6->3)->2,
(6->4)->2, (6->5)->3}, VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
v = FindVertexCut[g, 1, 4];
HighlightGraph[g, v]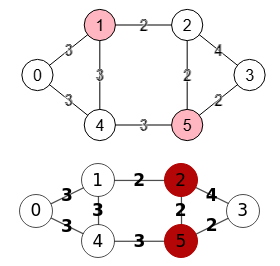
Para verificar que Wolfram ignora los pesos de las aristas, en la Figura vemos el corte de vértices "s=0" y "t=3" tras cambiar el peso 5 de la arista "0-1" por el menor peso 3, observando que obtenemos el corte de vértices "1,5" mientras que Wolfram sigue devolviendo el mismo corte "2,5".
Algoritmo findSTVertexCut()
A continuación presentamos el algoritmo findSTVertexCut() para encontrar el corte mínimo de vértices entre nodos "s" y "t":
function findSTVertexCut({matrix=[], firstIndex=0, lastIndex=0, methodFlow="findPath"}) {
let result = [], temp;
try {
let path = findPath({matrix, firstIndex, lastIndex});
if (typeof path==="string") throw new Error(path);
if (path.length>0) {
let n = matrix.length;
temp = getMatrixModeValue({matrix});
if (typeof temp==="string") throw new Error (temp);
let [modeValue, nullValue] = temp;
if (firstIndex===lastIndex) throw new Error(`First index and last index are equal`);
if (firstIndex<0 || firstIndex>=n) throw new Error(`First index is wrong`);
if (lastIndex<0 || lastIndex>=n) throw new Error(`Last index is wrong`);
if (!(matrix[firstIndex][lastIndex]===nullValue && matrix[lastIndex][firstIndex]===nullValue)) throw new Error(`First index and last index cannot be adjacent`);
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
let matrixCopy = JSON.parse(JSON.stringify(matrix));
if (!directed) {
if (temp = operateDirectionGraph({matrix:matrixCopy, edgesDirection:"directed-all"}), temp.error) throw new Error(temp.error);
matrixCopy = temp.matrix;
}
for (let index=0; index<n; index++) {
if (![firstIndex, lastIndex].includes(index) && (directed || index!==n+1)) {
if (temp = operateSplittingGraph({matrix:matrixCopy, index1:index, typeMergedValue:"sum"}), temp.error) throw new Error(temp.error);
}
}
let m = matrixCopy.length;
let k = directed ? n : n+1;
let maxNumber = Math.round((n*(n-1)/2) * (modeValue==="0/number" ? Math.max(...matrix.flat()) : 1));
for (let i=0; i<m; i++) {
for (let j=0; j<m; j++) {
if (matrixCopy[i][j]!==nullValue) {
if (!(i<k && j>=k)) {
let value = matrixCopy[i][j];
matrixCopy[i][j] = maxNumber;
}
}
}
}
if (temp = findSTEdgeCut({matrix:matrixCopy, firstIndex, lastIndex, methodFlow}), temp.error) throw new Error(temp.error);
result = temp.map(v => v[0]);
}
} catch(e){result = e.message}
return result;
}Para entender este algoritmo es necesario ver el de findSTEdgeCut() para el corte de aristas y a su vez entender como funciona findMaximumFlow() para el máximo flujo. Se usan las siguientes operaciones y algoritmos:
findPath()que encuentra todos los caminos entre dos nodos.getMatrixModeValue()para obtener el modo valores de la matriz.isGraphDirected()para saber si el grafo es dirigido.operateDirectionGraph()para convertir un grafo no dirigido en dirigido.operateSplittingGraph()para dividir nodos del grafo.
Al iniciar la ejecución comprobamos con findPath() que hay un camino entre los nodos "s" (firstIndex) y "t" (lastIndex) pues en otro caso no hay corte posible dado que esos nodos ya están en componentes distintos.
Dado que tenemos que modificar la matriz de adyacencia que nos viene por referencia, para no afectarla hacemos un copia de la misma con JSON.parse(JSON.stringify(matrix)). Si el grafo es no dirigido hacemos la conversión a dirigido como explicamos en los apartados anteriores y que puede también consultar en un tema anterior para convertir no dirigido en dirigido.
A continuación aplicamos la división (splitting) con operateSplittingGraph() a todos los nodos a excepción de "s" y "t". Y eventualmente para grafos no dirigidos también excluimos el nodo resultante de la subdivisión.
Encontramos el valor máximo maxNumber y se lo ponemos a todas las aristas menos a las resultantes de la división de nodos. Finalmente encontramos el corte mínimo de aristas entre "s" y "t" devolviendo la lista de vértices a partir de esas aristas que conforman el corte mínimo de vértices s-t.
Corte mínimo de vértices s-t adyacentes
En el algoritmo de findSTVertexCut() que vimos en el apartado anterior poníamos al inicio algunos controles para verificar que los nodos "s" y "t" que se pasan al algoritmo en los argumentos firstIndex y lastIndex se ajustan a algunos requisitos, como que no sean iguales o estén en el rango de los nodos o que no sean adyacentes. En la Figura vemos que al tratar de encontrar el corte mínimo entre "s=1" y "t=2" nos dice que el primer índice y último índice no pueden ser de nodos adyacentes.
Esto se basa en que no hay forma de separar los nodos "s=1" y "t=2" en distintos componentes sin eliminar la arista que los une "1-2". Y como estamos eliminando vértices y no aristas es por lo que se exige este requisito. Explicaremos más sobre esto en el apartado conectividad de vértices que explica el algoritmo getVertexConnectivity().
Puede importar el ejemplo con este JSON:
{"nodes":[
{"index":0,"nodeOffset":"-35 17.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"6.67 -27.5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"25 -52.5","parent":[{"index":1}]},
{"index":3,"nodeOffset":"66.67 -57.5","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-26.67 12.5","parent":[{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"8.33 -37.5","parent":[{"index":2},{"index":3},{"index":4}]}
],
"config":{
"algorithm":"Find s-t vertex cut",
"firstIndex":1,
"lastIndex":2
}}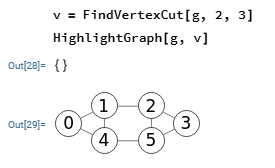
Si lo intentamos en Wolfram veremos que nos devuelve un resultado vacío {} lo que parece corroborar esa exigencia de que los nodos "s=1" y "t=2" no sean adyacentes. Recuerde que los índices de nodos en Wolfram se inician en 1 y en nuestra aplicación en 0, por lo que para Wolfram hemos de indicar "s=2" y "t=3", aunque los nodos aparezcan etiquetados iniciándose desde 0.
g = AdjacencyGraph[{{0,1,0,0,1,0},{1,0,1,0,1,0},{0,1,0,1,0,1},{0,0,1,0,0,1},{1,1,0,0,0,1},{0,0,1,1,1,0}},
ImageSize -> 150, VertexSize -> {"Scaled", 0.21}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center],
3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center], 6 -> Placed[5,Center]},
VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White,
EdgeStyle -> {{Black,Thickness[0.005]}}];
v = FindVertexCut[g, 2, 3];
HighlightGraph[g, v]Encontrar corte de vértices findVertexCut() en grafo no dirigido
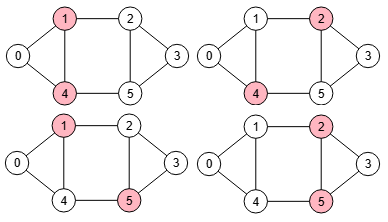
Con el algoritmo para encontrar cortes de vértices findVertexCut() aplicamos el algoritmo para encontrar corte mínimo de vértices s-t findSTVertexCut() a todas las parejas de nodos distintos "s" y "t" del grafo, nodos que también deben ser no adyacentes tal como se requiere para este último algoritmo.
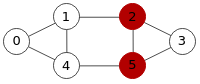
En la Figura vemos los cuatro únicos cortes de vértices que encontramos en un grafo no dirigido, todos de tamaño 2.
Find vertex cut: {
"vertices":[[1,4],[2,4],[1,5],[2,5]],
"values":[2,2,2,2],
"st":{"[1,4]":[[0,2],[0,3],[0,5]],
"[2,4]":[[1,3],[1,5],[5,0],[5,1]],
"[1,5]":[[2,0],[2,4],[4,2],[4,3]],
"[2,5]":[[3,0],[3,1],[3,4]]},
"stEmpty":[],
"stAdjacent":[[0,1],[0,4],[1,0],[1,2],[1,4],[2,1],[2,3],[2,5],[3,2],[3,5],[4,0],[4,1],[4,5],[5,2],[5,3],[5,4]],
"warnings":[]}En el resultado de findVertexCut() vemos varios campos. El primero "vertices" devuelve las cuatro listas de vértices [1,4], [2,4], [1,5] y [2,5] que vemos en la Figura. En "values" tenemos los valores de conectividad de cada uno de los cortes, que para este ejemplo supone una longitud de 2 nodos en cada uno de los cortes respectivamente. En "st" componemos un objeto con los cortes como claves y que parejas de nodos "s,t" producen ese corte. Por ejemplo, el corte [1,4] se produce con "s=0, t=2", "s=0, t=3" y "s=0, t=5". En "stEmpty" se relacionan, en su caso, las parejas "s,t" que no producen corte, mientras que en "stAdjacent" se relacionan las parejas "s,t" adyacentes que ya hemos dicho que no aplica el corte de vértices. Por último en "warnings" podríamos tener avisos, sobre lo cual veremos un ejemplo más abajo.
{"nodes":[
{"index":0,"nodeOffset":"-35 17.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"6.67 -27.5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"25 -52.5","parent":[{"index":1}]},
{"index":3,"nodeOffset":"66.67 -57.5","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-26.67 12.5","parent":[{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"8.33 -37.5","parent":[{"index":2},{"index":3},{"index":4}]}
],
"config":{
"lineHeight":18.75,
"algorithm":"Find vertex cut"
}}
En Figura vemos el resultado en Wolfram mostrando siempre un único mínimo corte, en este caso [2,5] igual que el último de nuestro resultado. Usa la función FindVertexCut[g] sin argumentos "s,t".
g = AdjacencyGraph[{{0,1,0,0,1,0},{1,0,1,0,1,0},{0,1,0,1,0,1},{0,0,1,0,0,1},{1,1,0,0,0,1},{0,0,1,1,1,0}},
ImageSize -> 200, VertexSize -> {"Scaled", 0.15}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center],
3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center], 6 -> Placed[5,Center]},
VertexLabelStyle -> Directive[Black,13.13], EdgeLabelStyle -> Directive[Black,13.13,Bold],
VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
e = FindVertexCut[g];
HighlightGraph[g, e]
Las opciones para ejecutar findVertexCut() se muestran en la Figura. La opción método para flujo se traslada a findSTEdgeCut() y de ahí a findMaximumFlow() pudiendo ser "findPath", "dijkstra" o "floyd" como ya vimos cuando expusimos esos algoritmos. El tipo conectividad vértices, que explicaremos con más detalle más abajo, puede ser alguno de la lista "vertices", "in-degrees", "out-degrees", "degrees", "in-weights", "out-weights" o "weights". En los ejemplos estamos usando el valor por defecto "vertices" que cuenta el número de vértices del corte.
Vamos a ver en el siguiente ejemplo el uso de la opción mínimo tamaño corte, que inicialmente aparece desmarcado.
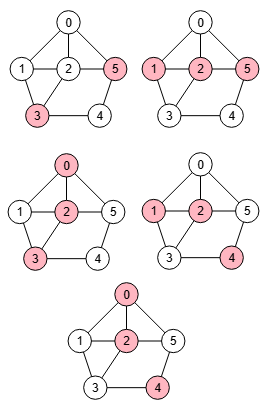
Si ejecutamos findVertexCut() con mínimo tamaño corte desmarcado encontraremos todos los cortes de vértices del grafo, devolviéndolos ordenados por su valor de conectividad. En Figura vemos los cinco cortes de vértices ordenados por su tamaño.
Marcando la opción mínimo tamaño corte devolverá sólo el primero de la lista [3,5], pero aún así el algoritmo tendrá que recuperarlos todos pues al final debe ordenarlos por la lista de valores de conectividad "values" para devolver el primero.
Encontrar corte vértices: {
"vertices":[[3,5],[1,2,5],[0,2,3],[1,2,4],[0,2,4]],
"values":[2,3,3,3,3],
"st":{"[3,5]":[[0,4],[1,4],[2,4],[4,0],[4,1],[4,2]],
"[1,2,5]":[[0,3]],
"[0,2,3]":[[1,5]],
"[1,2,4]":[[3,0],[3,5]],
"[0,2,4]":[[5,1],[5,3]]},
"stEmpty":[],
"stAdjacent":[[0,1],[0,2],[0,5],[1,0],[1,2],[1,3],[2,0],[2,1],[2,3],[2,5],[3,1],[3,2],[3,4],[4,3],[4,5],[5,0],[5,2],[5,4]],
"warnings":[]}Observe en el siguiente JSON para importar el ejemplo incluyendo la opción "minimumSizeCut":true.
{"nodes":[
{"index":0,"parent":[{"index":-1}]},
{"index":1,"parent":[{"index":0,"lineTextOffset":-0.8}]},
{"index":2,"parent":[{"index":0,"lineTextOffset":0.8},{"index":1,"lineTextOffset":"0 0.8"}]},
{"index":3,"parent":[{"index":1,"lineTextOffset":-0.8},{"index":4,"lineTextOffset":"0.5 0.8"},{"index":2,"lineTextOffset":0.8}]},
{"index":4,"parent":[{"index":5,"lineTextOffset":0.8}]},
{"index":5,"parent":[{"index":0,"lineTextOffset":0.8},{"index":2,"lineTextOffset":"0 0.8"}]}
],
"config":{
"lineHeight":18.75,
"algorithm":"Find vertex cut",
"minimumSizeCut":true
}}
Wolfram siempre devuelve el corte mínimo, como se observa en la Figura que devuelve también "3,5".
g = AdjacencyGraph[{{0,1,1,0,0,1},{1,0,1,1,0,0},{1,1,0,1,0,1},{0,1,1,0,1,0},{0,0,0,1,0,1},{1,0,1,0,1,0}},
ImageSize -> 141, VertexSize -> {"Scaled", 0.17}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center],
3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center], 6 -> Placed[5,Center]}, VertexLabelStyle -> Directive[Black,13.13],
EdgeLabelStyle -> Directive[Black,13.13,Bold], VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
e = FindVertexCut[g];
HighlightGraph[g, e]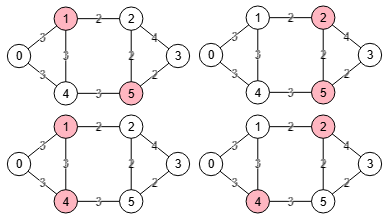
En la Figura vemos los cuatro cortes de mismo grafo que el expuesto al inicio de este apartado en la Figura, pero ahora como grafo ponderado. Obtenemos los mismos cortes [1,5],[2,5],[1,4],[2,4] pero ordenados por los valores de conectividad "15,15,17,17", cuando en el ejemplo no ponderado obteníamos [1,4],[2,4],[1,5],[2,5] con conectividades "2,2,2,2" que contaban el número de vértices en cada corte.
Find vertex cut: {
"vertices":[[1,5],[2,5],[1,4],[2,4]],
"values":[15,15,17,17],
"st":{"[1,5]":[[0,2],[0,3],[2,0],[2,4],[4,2],[4,3]],
"[1,4]":[[0,5]],
"[2,5]":[[1,3],[3,0],[3,1],[3,4]],
"[2,4]":[[1,5],[5,0],[5,1]]},
"stAdjacent":[[0,1],[0,4],[1,0],[1,2],[1,4],[2,1],[2,3],[2,5],[3,2],[3,5],[4,0],[4,1],[4,5],[5,2],[5,3],[5,4]],
"stEmpty":[],
"warnings":[]}Estamos usando la opción tipo conectividad vértices con valor "weights", pesos, que suma los pesos de las aristas entrantes y salientes de los vértices de corte. Observe por ejemplo que el primer corte "1,5" para el nodo "1" tenemos las aristas "0-1" con peso 3, "1-4" con peso 3 y "1-2" con peso 2 y para el nodo "5" tenemos las aristas "4-5" con peso 3, "2-5" con peso 2 y "5-3" con peso 2, sumando todos los pesos obtenemos 3+3+2+3+2+2 = 15 que es el primer valor de conectividad de la lista "15,15,17,17".
Los tipos de valores de conectividad "in-weights" y "out-weigths" para pesos de aristas entrantes y salientes respectivamente resultará en el mismo valor que "weights", pues en un grafo no dirigido todas las aristas son entrantes y salientes al mismo tiempo. Luego veremos un ejemplo con un grafo dirigido.
El otro tipo de valor de conectividad tiene que ver con los grados de los vértices que son el número de aristas que entran y salen del nodo. Así tenemos "in-degrees", "out-degrees" y "degrees", que para un grafo no dirigido son equivalentes, siendo para este grafo "6,6,6,6" para todos los cortes, pues todos los vértices de corte "1,2,4,5" que intervienen tienen grado 3 y como hay dos nodos por corte entonces tendremos esos valores 6.
Con este JSON se importa el ejemplo, observando la configuración "vertexConnectivityType":"weights" para informar al algoritmo que el tipo de conectividad será con pesos.
{"nodes":[
{"index":0,"nodeOffset":"-35 17.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"6.67 -27.5","parent":[{"index":0,"value":3}]},
{"index":2,"nodeOffset":"25 -52.5","parent":[{"index":1,"value":2}]},
{"index":3,"nodeOffset":"66.67 -57.5","parent":[{"index":2,"value":4}]},
{"index":4,"nodeOffset":"-26.67 12.5","parent":[{"index":0,"value":3},{"index":1,"value":3}]},
{"index":5,"nodeOffset":"8.33 -37.5","parent":[{"index":2,"value":2},{"index":3,"value":2},{"index":4,"value":3}]}
],
"config":{
"lineHeight":18.75,
"algorithm":"Find vertex cut",
"vertexConnectivityType":"weights"
}}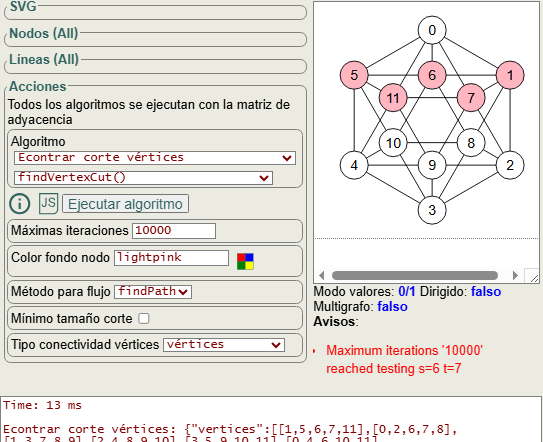
En la Figura vemos un grafo Platónico del tipo icosaédrico, donde el corte mínimo de vértices tiene tamaño 5.
Vemos en la Figura que la opción máximas iteraciones tiene valor inicial de 10000 iteraciones, tal que cuando el algoritmo alcanza ese máximo finaliza para evitar colapsar el navegador. Ofrece en color rojo el mensaje Maximum iterations '10000' reaching testing s=6 t=7
alcanzando ese máximo cuando estaba probando el corte entre "s=6" y "t=7". Como vemos en el resultado obtenido a continuación, hasta ese momento había alcanzado 7 resultados, pero al llegar al máximo de iteraciones no podemos asegurar que hayan más resultados.
Econtrar corte vértices: {
"vertices":[[1,5,6,7,11],[0,2,6,7,8],[1,3,7,8,9],[2,4,8,9,10],[3,5,9,10,11],[0,4,6,10,11],
[0,1,5,8,10]],
"values":[5,5,5,5,5,5,5],
"st":{"[1,5,6,7,11]":[[0,2],[0,3],[0,4],[0,8],[0,9],[0,10]],
"[0,2,6,7,8]":[[1,3],[1,4],[1,5],[1,9],[1,10],[1,11]],
"[1,3,7,8,9]":[[2,0],[2,4],[2,5],[2,6],[2,10],[2,11]],
"[2,4,8,9,10]":[[3,0],[3,1],[3,5],[3,6],[3,7],[3,11]],
"[3,5,9,10,11]":[[4,0],[4,1],[4,2],[4,6],[4,7],[4,8]],
"[0,4,6,10,11]":[[5,1],[5,2],[5,3],[5,7],[5,8],[5,9]],
"[0,1,5,8,10]":[[6,2],[6,3]]},
stEmpty":[],
"stAdjacent":[[0,1],[0,5],[0,6],[0,7],[0,11],[1,0],[1,2],[1,6],[1,7],[1,8],[2,1],
[2,3],[2,7],[2,8],[2,9],[3,2],[3,4],[3,8],[3,9],[3,10],[4,3],[4,5],[4,9],[4,10],
[4,11],[5,0],[5,4],[5,6],[5,10],[5,11],[6,0],[6,1],[6,5]],
"warnings":[["Maximum iterations '10000' reached testing s=6 t=7"]]}Incrementando hasta 20000 iteraciones máximas el algoritmo puede finalizar con un total de 12 cortes, pudiendo ahora asegurar el resultado. En amarillo se resalta un resultado que después veremos que obtiene Wolfram.
Encontrar corte vértices: {
"vertices":[[1,5,6,7,11],[0,2,6,7,8],[1,3,7,8,9],[2,4,8,9,10],[3,5,9,10,11],[0,4,6,10,11],
[0,1,5,8,10],[0,1,2,9,11],[1,2,3,6,10],[2,3,4,7,11],[3,4,5,6,8],[0,4,5,7,9]],
"values":[5,5,5,5,5,5,5,5,5,5,5,5],
"st":{"[1,5,6,7,11]":[[0,2],[0,3],[0,4],[0,8],[0,9],[0,10]],
"[0,2,6,7,8]":[[1,3],[1,4],[1,5],[1,9],[1,10],[1,11]],
"[1,3,7,8,9]":[[2,0],[2,4],[2,5],[2,6],[2,10],[2,11]],
"[2,4,8,9,10]":[[3,0],[3,1],[3,5],[3,6],[3,7],[3,11]],
"[3,5,9,10,11]":[[4,0],[4,1],[4,2],[4,6],[4,7],[4,8]],
"[0,4,6,10,11]":[[5,1],[5,2],[5,3],[5,7],[5,8],[5,9]],
"[0,1,5,8,10]":[[6,2],[6,3],[6,4],[6,7],[6,9],[6,11]],
"[0,1,2,9,11]":[[7,3],[7,4],[7,5],[7,6],[7,8],[7,10]],
"[1,2,3,6,10]":[[8,0],[8,4],[8,5],[8,7],[8,9],[8,11]],
"[2,3,4,7,11]":[[9,0],[9,1],[9,5],[9,6],[9,8],[9,10]],
"[3,4,5,6,8]":[[10,0],[10,1],[10,2],[10,7],[10,9],[10,11]],
"[0,4,5,7,9]":[[11,1],[11,2],[11,3],[11,6],[11,8],[11,10]]},
"stEmpty":[],
"stAdjacent":[[0,1],[0,5],[0,6],[0,7],[0,11],[1,0],[1,2],[1,6],[1,7],[1,8],[2,1],
[2,3],[2,7],[2,8],[2,9],[3,2],[3,4],[3,8],[3,9],[3,10],[4,3],[4,5],[4,9],[4,10],
[4,11],[5,0],[5,4],[5,6],[5,10],[5,11],[6,0],[6,1],[6,5],[6,8],[6,10],[7,0],
[7,1],[7,2],[7,9],[7,11],[8,1],[8,2],[8,3],[8,6],[8,10],[9,2],[9,3],[9,4],
[9,7],[9,11],[10,3],[10,4],[10,5],[10,6],[10,8],[11,0],[11,4],[11,5],[11,7],[11,9]],
"warnings":[]}Con el siguiente JSON puede importar ese ejemplo, observando que incluye "maxIter":20000 iteraciones necesarias para completar el resultado tal como comentamos antes, pues la configuración inicial es con 10000 iteraciones máximas, recordando que las configuraciones iniciales no se incluyen por defecto en el JSON.
{"nodes":[
{"index":0,"nodeOffset":"2.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"70.47 -5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"53.81 10","parent":[{"index":1}]},
{"index":3,"nodeOffset":"19.17 5","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-15.47 -40","parent":[{"index":3}]},
{"index":5,"nodeOffset":"-15.47 -5","parent":[{"index":0},{"index":4}]},
{"index":6,"nodeOffset":"2.5 -5","parent":[{"index":0},{"index":1},{"index":5}]},
{"index":7,"nodeOffset":"3.15 5","parent":[{"index":0},{"index":1},{"index":2}]},
{"index":8,"nodeOffset":"3.15","parent":[{"index":1},{"index":2},{"index":3},{"index":6}]},
{"index":9,"nodeOffset":"-14.17 -15","parent":[{"index":2},{"index":3},{"index":4},{"index":7}]},
{"index":10,"nodeOffset":"-31.49 -50","parent":[{"index":3},{"index":4},{"index":5},{"index":6},{"index":8}]},
{"index":11,"nodeOffset":"-48.15 5","parent":[{"index":0},{"index":4},{"index":5},{"index":7},{"index":9}]}
],
"config":{
"algorithm":"Find vertex cut",
"maxIter":20000
}}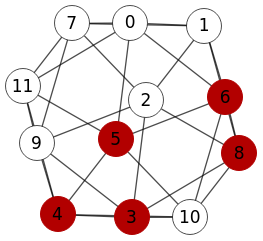
En la Figura vemos que Wolfram devuelve el corte [3,4,5,6,8] que es uno de los que resaltamos en el resultado obtenido más arriba.
g = AdjacencyGraph[{{0,1,0,0,0,1,1,1,0,0,0,1},{1,0,1,0,0,0,1,1,1,0,0,0},{0,1,0,1,0,0,0,1,1,1,0,0},{0,0,1,0,1,0,0,0,1,1,1,0},
{0,0,0,1,0,1,0,0,0,1,1,1},{1,0,0,0,1,0,1,0,0,0,1,1},{1,1,0,0,0,1,0,0,1,0,1,0},{1,1,1,0,0,0,0,0,0,1,0,1},{0,1,1,1,0,0,1,0,0,0,1,0},
{0,0,1,1,1,0,0,1,0,0,0,1},{0,0,0,1,1,1,1,0,1,0,0,0},{1,0,0,0,1,1,0,1,0,1,0,0}}, ImageSize -> 263, VertexSize -> {"Scaled", 0.12},
VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center], 3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center],
6 -> Placed[5,Center], 7 -> Placed[6,Center], 8 -> Placed[7,Center], 9 -> Placed[8,Center], 10 -> Placed[9,Center], 11 -> Placed[10,Center],
12 -> Placed[11,Center]}, VertexLabelStyle -> Directive[Black,17.5], EdgeLabelStyle -> Directive[Black,17.5,Bold], VertexStyle -> White,
EdgeStyle -> {{Black,Thickness[0.005]}}];
e = FindVertexCut[g];
HighlightGraph[g, e]Encontrar corte de vértices findVertexCut() en grafo dirigido
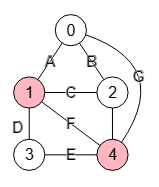
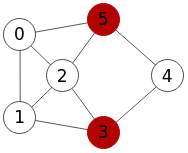
En el apartado anterior vimos ejemplos de corte de vértices en grafos no dirigidos, como el de la Figura que tiene un único corte [1,4]. Vea que las únicas combinaciones de nodos "s" y "t" no adyacentes son "0,3" y "2,3" y, por ser no dirigido, sus inversos "3,0" y "3,2". Todas estas parejas "s,t" producen el mismo y único corte [1,4].
Encontrar corte vértices: {
"vertices":[[1,4]],
"values":[2],
"st":{"[1,4]":[[0,3],[2,3],[3,0],[3,2]]},
"stEmpty":[],
"stAdjacent":[[0,1],[0,2],[0,4],[1,0],[1,2],[1,3],[1,4],[2,0],[2,1],[2,4],[3,1],[3,4],[4,0],[4,1],[4,2],[4,3]],
"warnings":[]}
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4,"value":"G","lineOffset":"6 -2","lineType":"quadratic"}]},
{"index":1,"parent":[{"index":0,"value":"A"}]},
{"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"C"}]},
{"index":3,"parent":[{"index":1,"value":"D","lineTextOffset":"-0.75 0.25"},{"index":4,"value":"E"}]},
{"index":4,"parent":[{"index":1,"value":"F"},{"index":2}]}
],
"config":{
"algorithm":"Find vertex cut"
}}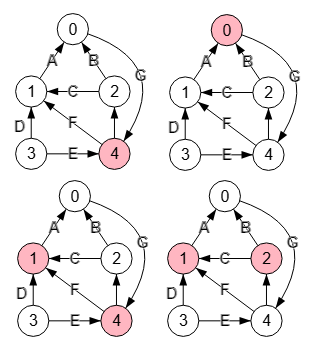
Cuando pasamos a grafos dirigidos los resultados que se obtienen pueden diferir mucho. En la Figura vemos el mismo grafo con el mismo etiquetado (también no ponderado) pero en este caso dirigido. Observe que con "s=3, t=0" produce el corte [1,4], el mismo que vimos antes y también al inicio de este tema en la Figura usando el algoritmo findSTVertexCut().
Pero ahora además encuentra otros cortes [4], [0] y [1,2]. Observe en el siguiente resultado que ahora hay menos parejas "s,t" adyacentes pues las direcciones lo posibilitan. Además se producen parejas donde no hay camino entre "s" y "t" que vemos en el campo "stEmpty", parejas que se descartan pues si no hay camino entre ellos ya esos dos nodos están en componentes conectados distintos y, por tanto, no procede aplicar corte.
Find vertex cut: {
"vertices":[[4],[0],[1,4],[1,2]],
"values":[1,1,2,2],
"st":{"[4]":[[0,1],[0,2],[3,2]],
"[0]":[[1,2],[1,4],[2,4]],
"[1,4]":[[3,0]],
"[1,2]":[[4,0]]},
"stEmpty":[[0,3],[1,3],[2,3],[4,3]],
"stAdjacent":[[0,4],[1,0],[2,0],[2,1],[3,1],[3,4],[4,1],[4,2]],
"warnings":[]Como hemos dicho, encontrar todos los cortes de vértices supone iterar por todas las parejas "s,t" de nodos no adyacentes y encontrar el corte mínimo de vértices devolviéndolos ordenados creciente por el valor de conectividad de vértices que hayamos especificado. Y encontrar un corte mínimo de vértices s-t supone encontrar un conjunto mínimo de vértices que separe los nodos "s" y "t" en distintos componentes conectados. Cuando estemos con grafos dirigidos hemos de entenderlo como distintos componentes fuertemente conectados.
Observe que el grafo de este ejemplo tiene 2 componentes fuertemente conectados, uno es el nodo "3" y el otro los nodos "0,1,2,4" como ya vimos en un tema anterior. El primer corte con el único nodo "4" separa "s,t" para las parejas "0,1", "0,2" y "3,2" pues al eliminar el nodo "4" tendremos 4 componentes conectados "0", "1", "2" y "3" estando "s" y "t" en dos componentes distintos. Para el segundo corte "0" con "s,t" siendo "1,2", "1,4" y "2,4" pasa lo mismo pues al eliminar el "0" tendremos 4 componentes "1", "2", "3" y "4" estando "s,t" en distintos componentes. Eliminando los nodos del tercer o cuarto corte "1,4" y "1,2" pasamos de 2 componentes a 3 componentes estando "s,t" que en el primer caso es "3,0" y en el segundo "4,0" en dos componentes distintos.
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4,"value":"G","lineOffset":"6 -2","lineType":"quadratic"}]},
{"index":1,"parent":[{"index":0,"value":"A"}]},
{"index":2,"parent":[{"index":0,"value":"B"},{"index":1,"value":"C"}]},
{"index":3,"parent":[{"index":1,"value":"D","lineTextOffset":"-0.75 0.25"},{"index":4,"value":"E"}]},
{"index":4,"parent":[{"index":1,"value":"F"},{"index":2}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find vertex cut"
}}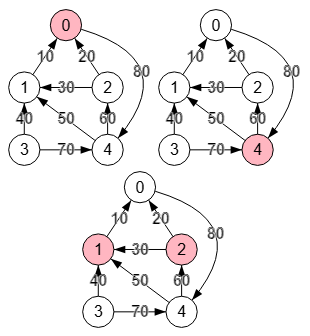
En la Figura vemos el mismo grafo pero ahora ponderado. Para "s=3, t=0" encontramos el corte [1,2] que es el mismo que encontramos en la Figura cuando exponíamos el algoritmo findSTVertexCut() para ese "s-t" con el mismo grafo ponderado ¿Y dónde está el corte [1,4]?
En el mismo grafo pero no ponderado de la Figura para "s=3, t=0" produce el corte [1,4] mientras que aquí produce [1,2], con ambos cortes separando "3" y "0" en dos componentes. Así que los pesos de las aristas influyen mucho en los cortes encontrados, pues no hay que olvidar que estos algoritmos usan findMaximumFlow() basado en los pesos de las aristas.
Find vertex cut: {
"vertices":[[0],[4],[1,2]],
"values":[30,150,180],
"st":{"[4]":[[0,1],[0,2],[3,2]],
"[0]":[[1,2],[1,4],[2,4]],
"[1,2]":[[3,0],[4,0]]},
"stEmpty":[[0,3],[1,3],[2,3],[4,3]],
"stAdjacent":[[0,4],[1,0],[2,0],[2,1],[3,1],[3,4],[4,1],[4,2]],
"warnings":[]}Usando el tipo conectividad vértices "in-weights" (pesos de entrada), observamos los valores [30,150,180] en el campo "values". Para el primer corte [0] los pesos de entrada de ese vértice "0" son 10+20 = 30. Para el segundo corte [4] resultan 70+80 = 150. Y para el tercero [1,2] son 40+50+30+60 = 180. Se ordenan por estos valores siendo por tanto el primero corte [0] el que se califica como corte mínimo, mínimo en relación con el peso de las aristas entrantes pues esa es la configuración que le pasamos al algoritmo.
Con el siguiente JSON se importa el ejemplo, observando la configuración vertexConnectivityType":"in-weights".
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4,"lineType":"quadratic","lineOffset":"7 -2","value":80}]},
{"index":1,"parent":[{"index":0,"value":10}]},
{"index":2,"parent":[{"index":0,"value":20},{"index":1,"value":30}]},
{"index":3,"parent":[{"index":1,"value":40},{"index":4,"value":70}]},
{"index":4,"parent":[{"index":1,"value":50},{"index":2,"value":60}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find vertex cut",
"vertexConnectivityType":"in-weights"
}}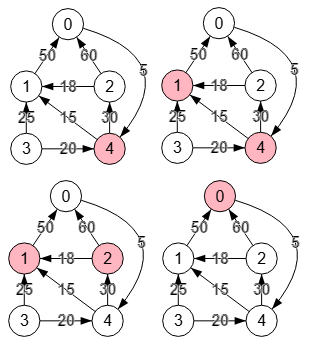
Modificando los pesos de las aristas volvemos a ver en la Figura el corte [1,4] para "s=3, t=0".
Encontrar corte vértices: {
"vertices":[[4],[1,4],[1,2],[0]],
"values":[25,83,88,110],
"st":{"[4]":[[0,1],[0,2],[1,2],[3,2]],
"[1,4]":[[3,0]],
"[0]":[[1,4],[2,4]],
"[1,2]":[[4,0]]},
"stEmpty":[[0,3],[1,3],[2,3],[4,3]],
"stAdjacent":[[0,4],[1,0],[2,0],[2,1],[3,1],[3,4],[4,1],[4,2]],
"warnings":[]}
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4,"lineType":"quadratic","lineOffset":"7 -2","value":5}]},
{"index":1,"parent":[{"index":0,"value":50}]},
{"index":2,"parent":[{"index":0,"value":60},{"index":1,"value":18}]},
{"index":3,"parent":[{"index":1,"value":25},{"index":4,"value":20}]},
{"index":4,"parent":[{"index":1,"value":15},{"index":2,"value":30}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find vertex cut",
"vertexConnectivityType":"in-weights"
}}
En la Figura vemos el resultado en Wolfram del grafo ponderado de la Figura. Como ya hemos dicho, Wolfram parece ignorar los pesos, pues con pesos o sin pesos siempre devuelve el corte "1,4" e incluso como si el grafo es no dirigido se obtiene el mismo resultado que también vimos en la Figura.
g = WeightedAdjacencyGraph[{{∞,∞,∞,∞,80},{10,∞,∞,∞,∞},{20,30,∞,∞,∞},{∞,40,∞,∞,70},{∞,50,60,∞,∞}},
ImageSize -> 188, VertexSize -> {"Scaled", 0.17}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center],
3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center]}, VertexLabelStyle -> Directive[Black,17.5],
EdgeLabelStyle -> Directive[Black,17.5,Bold], EdgeLabels -> {(1->5)->80, (2->1)->10, (3->1)->20, (3->2)->30,
(4->2)->40, (4->5)->70, (5->2)->50, (5->3)->60}, VertexStyle -> White, DirectedEdges -> True,
EdgeStyle -> {{Black,Thickness[0.005]}}];
e = FindVertexCut[g];
HighlightGraph[g, e]Algoritmo findVertexCut()
A continuación vemos el algoritmo de findVertexCut().
function findVertexCut({matrix=[], minimumSizeCut=false, vertexConnectivityType="vertices", methodFlow="findPath"}) {
let result = {vertices: [], values: [], st: [], stEmpty: [], stAdjacent: []}, temp, tempIter;
result.warnings = [];
try {
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
temp = getMatrixModeValue({matrix});
if (typeof temp==="string") throw new Error (temp);
let [modeValue, nullValue] = temp;
let n = matrix.length;
let sets = new Set();
let sts = {};
for (let firstIndex=0; firstIndex<n; firstIndex++) {
let br = false;
for (let lastIndex=0; lastIndex<n; lastIndex++) {
if (firstIndex!==lastIndex) {
if (matrix[firstIndex][lastIndex]!==nullValue) {
result.stAdjacent.push([firstIndex, lastIndex]);
} else {
let tempIter = iter;
iter = 0;
let path = findPath({matrix, firstIndex, lastIndex});
if (typeof path==="string") throw new Error("(findPath) " + path);
iter = tempIter;
if (path.length===0) {
result.stEmpty.push([firstIndex, lastIndex]);
} else {
if (iter++, iter>maxIter) {
result.warnings.push([`Maximum iterations '${maxIter}' reached testing s=${firstIndex} t=${lastIndex}`]);
br = true;
break;
}
temp = findSTVertexCut({matrix, firstIndex, lastIndex, methodFlow});
if (typeof temp==="string") {
result.warnings.push("(findSTVertexCut) " + temp + ` testing s=${firstIndex} t=${lastIndex}`);
} else if (temp.length>0) {
let vertices = temp;
let verticesStr = JSON.stringify(vertices);
sets.add(verticesStr);
if (!sts.hasOwnProperty(verticesStr)) sts[verticesStr] = [];
sts[verticesStr].push([firstIndex, lastIndex]);
}
}
}
}
}
if (br) break;
}
let vertices = [...sets].map(v => JSON.parse(v));
temp = getVertexConnectivityValues({matrix, vertices, vertexConnectivityType});
if (typeof temp==="string") throw new Error(temp);
vertices = temp.vertices;
let values = temp.values;
if (minimumSizeCut) {
result.vertices = [vertices[0]];
result.values.push(values[0]);
} else {
result.vertices = vertices;
result.values = values;
}
result.st = sts;
} catch(e){result = e.message}
return result;
}Usa las siguientes funciones:
isGraphDirected()para saber si el grafo es dirigido.getMatrixModeValue()para obtener el modo valores de la matriz.findPath()que encuentra todos los caminos entre dos nodos.findSTVertexCut()que encuentra el corte mínimo de vértices s-t.
Iteramos por todas las parejas de nodos "s" y "t" (firstIndex y lastIndex) omitiendo las que sean adyacentes o no haya un camino entre esos nodos usando findPath(). Encuentra el corte mínimo de vértices "s-t" con findSTVertexCut() que vimos en los primeros apartados de este tema. Como más de una pareja "s,t" puede dar lugar al mismo corte de vértices, vamos guardando esos cortes en un conjunto del tipo Set de JavaScript, que almacenará valores únicos en la variable sets y que se devolverá en el resultado en el campo "vertices". La variable sts es un objeto de JavaScript donde las claves son el corte de vértices y los valores son las parejas "s,t" que producen ese corte devolviéndose en la variable "st" del resultado.
Tras finalizar la iteración de todas las parejas "s,t" tendremos en sets todos los cortes de vértices sin orden definido, debiendo ordenarse por el tipo de conectividad. Para ello usaremos el algoritmo getVertexConnectivityValues() para obtener los valores de conectividad de vértices y ordenar los cortes según el mínimo de esos valores, devolviéndo también la lista con esos valores que luego se devolverá en el campo "values" del resultado de findVertexCut(). Si se pasa la opción mínimo tamaño corte entonces se devolverá sólo el primer corte. Usa a su vez los siguientes algoritmos:
getVertexDegreespara obtener los grafos de los vértices.getVertexInOutDegreespara grados entrada/salida de los vértices.
// vertexConnectivityType = "vertices", "in-degrees", "out-degrees", "degrees", "in-weights", "out-weights", "weights"
function getVertexConnectivityValues({matrix=[], vertices=[], vertexConnectivityType="vertices"}) {
let result = {vertices: [], values: []}, temp;
try {
let n = matrix.length;
if (vertexConnectivityType==="vertices"){
result.vertices = vertices.toSorted((v,w) => v.length-w.length);
result.values = result.vertices.map(v => v.length);
} else if (vertexConnectivityType.indexOf("degrees")>-1) {
let vct = vertexConnectivityType==="in-degrees" ? "in" : vertexConnectivityType==="out-degrees" ? "out" : "inout";
if (vct==="inout") {
if (temp = getVertexDegrees({matrix}), typeof temp==="string") throw new Error(temp);
} else {
if (temp = getVertexInOutDegrees({matrix}), typeof temp==="string") throw new Error(temp);
}
let degrees = temp;
let values = [];
for (let item of vertices) {
let sum = item.reduce((p,v) => {
if (vct==="in") {
p += degrees[v][0];
} else if (vct==="out"){
p += degrees[v][1];
} else {
p += degrees[v];
}
return p;
}, 0)
values.push([item, sum]);
}
values.sort((v, w) => v[1]-w[1]);
for (let [item, value] of values.values()) {
result.vertices.push(item);
result.values.push(value);
}
} else if (vertexConnectivityType.indexOf("weights")>-1) {
let directed = isGraphDirected({matrix});
if (typeof directed==="string") throw new Error(directed);
let vct = vertexConnectivityType==="in-weights" ? "in" : vertexConnectivityType==="out-weights" ? "out" : "inout";
let order = [];
for (let item of vertices) {
let sum = 0;
for (let vertex of item) {
for (let i=0; i<n; i++) {
if (vct==="in") {
sum += matrix[i][vertex];
} else if (vct==="out") {
sum += matrix[vertex][i];
} else {
sum += matrix[i][vertex];
if (directed) sum += matrix[vertex][i];
}
}
}
order.push([item, sum]);
}
order.sort((v,w) => v[1]-w[1]);
result.vertices = order.map(v => v[0]);
result.values = order.map(v => v[1]);
}
} catch(e){result = e.message}
return result;
}Comparar conjunto separador de vértices y corte de vértices

Vimos en un tema anterior que encontrar un conjunto separador de vértices con tamaño "k" supone encontrar "k" vértices cuya eliminación hace que se incremente el número de componentes conectados del grafo. Mientras que encontrar todos los cortes de vértices supone iterar por todas las parejas "s,t" de nodos no adyacentes y encontrar el corte mínimo de vértices que separa "s" y "t" en distintos componentes conectados y devolviendo todos los cortes mínimos ordenados creciente por el valor de conectividad de vértices que hayamos especificado. Por lo tanto es importante entender que son dos cosas diferentes.
En la Figura vemos los 4 cortes de vértices de un grafo no dirigido que ya vimos al inicio de este tema.
Find vertex cut: {
"vertices":[[1,4],[2,4],[1,5],[2,5]],
"values":[6,6,6,6],
"st":{"[1,4]":[[0,2],[0,3],[0,5]],
"[2,4]":[[1,3],[1,5],[5,0],[5,1]],
"[1,5]":[[2,0],[2,4],[4,2],[4,3]],
"[2,5]":[[3,0],[3,1],[3,4]]},
"stEmpty":[],
"stAdjacent":[[0,1],[0,4],[1,0],[1,2],[1,4],[2,1],[2,3],[2,5],[3,2],[3,5],[4,0],[4,1],[4,5],[5,2],[5,3],[5,4]],
"warnings":[]}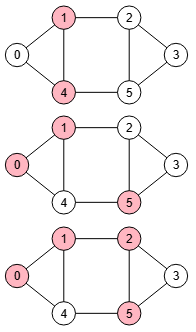
Mientras que en la Figura vemos una primera muestra de cada conjunto separador de vértices con k=2,3,4 no habiendo de tamaño 1 ni superiores a 4. De tamaño k=2 hay 4 conjuntos separadores [[1,4], [1,5], [2,4], [2,5]], de tamaño k=3 tenemos 10 conjuntos separadores [[0,1,5], [0,2,4], [0,2,5], [1,2,4], [1,2,5], [1,3,4], [1,3,5], [1,4,5], [2,3,4], [2,4,5]] y de tamaño 4 hay 7 conjuntos separadores [[0,1,2,5], [0,1,3,5], [0,2,3,4], [0,2,4,5], [1,2,3,4], [1,2,4,5], [1,3,4,5]]. Se observa que para este grafo los cortes de vértices coinciden con los conjuntos separadores de tamaño k=2.
{"nodes":[
{"index":0,"nodeOffset":"-35 17.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"6.67 -27.5","parent":[{"index":0}]},
{"index":2,"nodeOffset":"25 -52.5","parent":[{"index":1}]},
{"index":3,"nodeOffset":"66.67 -57.5","parent":[{"index":2}]},
{"index":4,"nodeOffset":"-26.67 12.5","parent":[{"index":0},{"index":1}]},
{"index":5,"nodeOffset":"8.33 -37.5","parent":[{"index":2},{"index":3},{"index":4}]}
],
"config":{
"lineHeight":18.75,
"algorithm":"Find vertex separator",
"findAll":true,
"sizeSeparator":2
}}Obtener conectividad vértices getVertexConnectivity()

Obtener la conectividad de vértices es algo más complejo que obtener la conectividad de aristas, que para un grafo no ponderado se definía como el mínimo número de aristas que al eliminarlas generaban un corte mínimo de aristas. Para un grafo ponderado en lugar de devolver el número de aristas sumábamos los pesos de esas aristas.
Por el teorema de Menger para dos vértices "s" y "t" la conectividad de vértices s-t, que se denomina κ(s, t) y la conectividad de aristas s-t, que se denomina λ(s, t), se pueden calcular usando el algoritmo del máximo flujo y mínimo corte, tal como hacemos en nuestra aplicación. κ(s, t) o λ(s, t) son los tamaños más pequeños del corte de vértices o aristas respectivamente que separan "s" y "t" en dos componentes distintos.
La conectividad de vértices del grafo se calcula como el mínimo de todos los valores κ(s, t) para todas las parejas de nodos no adyacentes. Y la conectividad de aristas del grafo se calcula como el mínimo de todos los valores λ(s, t) para todas las parejas de nodos sin el requisito de no adyacencia.
El requisito de no adyacencia para el corte de vértices es que si entre "s" y "t" hay una arista "s-t" en no dirigidos o "s🡒t" en dirigidos, no hay forma de separar esos nodos en dos componentes si no es eliminando esa arista "s-t" o "s🡒t". Y en el corte de vértices se trata de buscar los vértices, no las aristas, que al eliminarlos separan "s" y "t".
Para el corte de vértices así como para obtener la conectividad de vértices agregamos en la aplicación la opción tipo conectividad de vértices que puede ser número de vértices (vertices), grados de entrada de los vértices (in-degrees), grados de salida de los vértices (out-degrees), grados de los vértices (degrees), pesos de entrada de los vértices (in-weights), pesos de salida de los vértices (out-weights) y pesos de los vértices (weights). Los pesos se refieren a las aristas de entrada, salida o ambas a cada vértice del corte.
Podemos obtener la conectividad del mínimo corte o marcando la opción modo s-t e indicando el primer índice nodo y último índice nodo para identificar los vértices "s" y "t" devolviendo la conectividad para ese corte "s-t".
El tipo de conectividad puede afectar a la obtención del mínimo corte, como ya hemos visto en apartados anteriores, especialmente para grafos dirigidos pues en no dirigidos no se observa, como el de la Figura que ya vimos más arriba en la Figura. Expone los 4 cortes de vértices ordenados por tipo conectividad pesos entrada (in-weight), siendo el corte mínimo el primero de ellos con los vértices [1,5] tal como se ve en el resultado de findVertexCut():
Encontrar corte vértices: {
"vertices":[[1,5],[2,5],[1,4],[2,4]],
"values":[15,15,17,17],
"st":{"[1,5]":[[0,2],[0,3],[2,0],[2,4],[4,2],[4,3]],
"[1,4]":[[0,5]],
"[2,5]":[[1,3],[3,0],[3,1],[3,4]],
"[2,4]":[[1,5],[5,0],[5,1]]},
"stEmpty":[],
"stAdjacent":[[0,1],[0,4],[1,0],[1,2],[1,4],[2,1],[2,3],[2,5],[3,2],[3,5],[4,0],[4,1],[4,5],[5,2],[5,3],[5,4]],
"warnings":[]}
Obtener conectividad vértices:
{"value":15,"warnings":[]}Si ejecutamos getVertexConnectivity() para ese grafo con el mismo tipo de conectividad pesos de entrada (in-weights) obtenemos el resultado 15, el mismo que vemos resaltado en azul en la lista de "vertices" y "values" en el resultado anterior.
| Tipo conectividad | Corte mínimo | Conecti- vidad |
|---|---|---|
| Vértices (vertices) | [1,5] | 2 |
| Grados entrada (in-degrees) | [1,5] | 6 |
| Grados salida (out-degrees) | [1,5] | 6 |
| Grados (degrees) | [1,5] | 6 |
| Pesos entrada (in-weights) | [1,5] | 15 |
| Pesos salida (out-weights) | [1,5] | 15 |
| Pesos (weights) | [1,5] | 15 |
Ejecutando findVertexCut() y getVertexConnectivity() para los distintos tipos de conectividad volcamos en la tabla anterior los resultados. Vemos que en todos los casos se obtiene el corte [1,5] y que todos los grados y pesos son iguales entre sí. En vértices la conectividad es 2 pues son 2 los vértices del corte [1,5]. En grados de entrada o salida son 6 pues cada vértice tiene 3 aristas entrantes que también pueden considerarse salientes. Sin embargo en grados también son 6 pues cada vértice tiene grado 3. En pesos pasa algo parecido, sumando los pesos de las aristas de los nodos "1" y "5" obtenemos 3+3+2+3+2+2 = 15.
{"nodes":[
{"index":0,"nodeOffset":"-35 17.5","parent":[{"index":-1}]},
{"index":1,"nodeOffset":"6.67 -27.5","parent":[{"index":0,"value":3}]},
{"index":2,"nodeOffset":"25 -52.5","parent":[{"index":1,"value":2}]},
{"index":3,"nodeOffset":"66.67 -57.5","parent":[{"index":2,"value":4}]},
{"index":4,"nodeOffset":"-26.67 12.5","parent":[{"index":0,"value":3},{"index":1,"value":3}]},
{"index":5,"nodeOffset":"8.33 -37.5","parent":[{"index":2,"value":2},{"index":3,"value":2},{"index":4,"value":3}]}
],
"config":{
"lineHeight":18.75,
"algorithm":"Find vertex cut",
"vertexConnectivityType":"in-weights"
}}
En la Figura vemos un grafo dirigido y ponderado con tipo conectividad pesos entrada (in-weights), ejemplo que ya vimos en un apartado anterior en la Figura.
Ejecutando findVertexCut() vemos que el mínimo corte es [0] con valor conectividad 30, tal como observamos en el resultado obtenido:
Find vertex cut: {
"vertices":[[0],[4],[1,2]],
"values":[30,150,180],
"st":{"[4]":[[0,1],[0,2],[3,2]],
"[0]":[[1,2],[1,4],[2,4]],
"[1,2]":[[3,0],[4,0]]},
"stEmpty":[[0,3],[1,3],[2,3],[4,3]],
"stAdjacent":[[0,4],[1,0],[2,0],[2,1],[3,1],[3,4],[4,1],[4,2]],
"warnings":[]}
Obtener conectividad vértices:
{"value":30,"warnings":[]}Ejecutando getVertexConnectivity con el mismo tipo conectividad pesos entrada obtendremos ese valor 30.
| Tipo conectividad | Corte mínimo | Conecti- vidad |
|---|---|---|
| Vértices (vertices) | [4] | 1 |
| Grados entrada (in-degrees) | [4] | 2 |
| Grados salida (out-degrees) | [0] | 1 |
| Grados (degrees) | [0] | 3 |
| Pesos entrada (in-weights) | [0] | 30 |
| Pesos salida (out-weights) | [1,2] | 60 |
| Pesos (weights) | [0] | 110 |
En la tabla anterior volcamos los cortes mínimos y los valores de conectividad para los distintos tipos. Observamos que ahora los cortes pueden ser diferentes según el tipo de conectividad.
{"nodes":[
{"index":0,"parent":[{"index":-1},{"index":4,"lineType":"quadratic","lineOffset":"7 -2","value":80}]},
{"index":1,"parent":[{"index":0,"value":10}]},
{"index":2,"parent":[{"index":0,"value":20},{"index":1,"value":30}]},
{"index":3,"parent":[{"index":1,"value":40},{"index":4,"value":70}]},
{"index":4,"parent":[{"index":1,"value":50},{"index":2,"value":60}]}
],
"config":{
"markerEnd":"arrow",
"algorithm":"Find vertex cut",
"minimumSizeCut":true,
"vertexConnectivityType":"in-weights"
}}En Wolfram para el grafo no dirigido y ponderado de Figura se obtiene un valor de conectividad 2 que es igual que el tipo de conectividad de vértices que nosotros obtuvimos. Usa la función VertexConnectivity a la que también pueden pasarse optativamente los argumentos "s" y "t" como en nuestra aplicación.
g = WeightedAdjacencyGraph[{{∞,3,∞,∞,3,∞},{3,∞,2,∞,3,∞},{∞,2,∞,4,∞,2},{∞,∞,4,∞,∞,2},{3,3,∞,∞,∞,3},{∞,∞,2,2,3,∞}},
ImageSize -> 113, VertexSize -> {"Scaled", 0.21}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center],
3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center], 6 -> Placed[5,Center]}, VertexLabelStyle -> Directive[Black,13.13],
EdgeLabelStyle -> Directive[Black,13.13,Bold], EdgeLabels -> {(2->1)->3, (3->2)->2, (4->3)->4, (5->1)->3, (5->2)->3,
(6->3)->2, (6->4)->2, (6->5)->3}, VertexStyle -> White, EdgeStyle -> {{Black,Thickness[0.005]}}];
VertexConnectivity[g]Para el grafo dirigido y ponderado de la Figura Wolfram devuelve un valor 0 para la conectividad del grafo, mientras que para los nodos "s=3" y "t=0" devuelve 2. Por un lado Wolfram dice que para grafos desconectados se devolverá 0 y ese grafo es desconectado aunque tiene 2 componentes fuertemente conectados. Y por otro Wolfram ignora los pesos así que la conectividad entre "s=3" y "t=0" es 2 pues como explicamos en apartados anteriores para este mismo ejemplo, Wolfram siempre obtiene el mismo corte [1,4] con o sin pesos y 2 es el número de vértices de ese corte.
g = WeightedAdjacencyGraph[{{∞,∞,∞,∞,80},{10,∞,∞,∞,∞},{20,30,∞,∞,∞},{∞,40,∞,∞,70},{∞,50,60,∞,∞}},
ImageSize -> 188, VertexSize -> {"Scaled", 0.17}, VertexLabels -> {1 -> Placed[0,Center], 2 -> Placed[1,Center],
3 -> Placed[2,Center], 4 -> Placed[3,Center], 5 -> Placed[4,Center]}, VertexLabelStyle -> Directive[Black,17.5],
EdgeLabelStyle -> Directive[Black,17.5,Bold], EdgeLabels -> {(1->5)->80, (2->1)->10, (3->1)->20, (3->2)->30,
(4->2)->40, (4->5)->70, (5->2)->50, (5->3)->60}, VertexStyle -> White, DirectedEdges -> True,
EdgeStyle -> {{Black,Thickness[0.005]}}];
VertexConnectivity[g]
VertexConnectivity[g, 4, 1]El JavaScript de getVertexConnectivity() que se expone a continuación usa findSTVertexCut() que encuentra el corte mínimo de vértices s-t, findVertexCut() que encuentra corte vértices y getVertexConnectivityValues() que ya vimos con ese algoritmo.
Si la opción modeST es verdadera entonces se aplica findSTVertexCut() para obtener el corte mínimo de vértices "s,t" que se corresponden con los argumentos firstIndex y lastIndex. En este caso también hemos de llamar a getVertexConnectivityValues() para obtener el valor de conectividad. En otro caso con modeST = false se ejecuta findVertexCut() que también usa internamente getVertexConnectivityValues() para ordenar todos los cortes por el menor valor de conectividad según el tipo que se pase en el argumento vertexConnectivityType.
function getVertexConnectivity({matrix=[], firstIndex=0, lastIndex=0, modeST=false, vertexConnectivityType="vertices", methodFlow="findPath"}) {
let result = {value: 0, warnings: []}, temp;
try {
if (modeST) {
temp = findSTVertexCut({matrix, firstIndex, lastIndex, methodFlow});
} else {
temp = findVertexCut({matrix, minimumSizeCut:true, vertexConnectivityType, methodFlow});
result.warnings = temp.warnings;
}
if (typeof temp==="string") throw new Error(temp);
if (modeST) {
let vertices = [temp];
temp = getVertexConnectivityValues({matrix, vertices, vertexConnectivityType});
if (typeof temp==="string") throw new Error(temp);
}
result.value = typeof temp.values[0]==="number" ? temp.values[0] : 0;
} catch(e){result = e.message}
return result;
}