18 sep 2025

Búsquedas en un grafo

Búsqueda en profundidad en un grafo (iterativo) `getDepthFirstSearchIterative()`

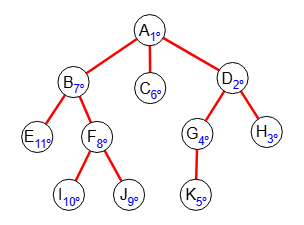
*Figura*. Búsqueda en profundidad en un árbol (iterativo)

El algoritmo de búsqueda primero en profundidad, en inglés Depth-first search y su abreviatura DFS, recorre el grafo empezando en un nodo que se indique atravesando los nodos primero hacia abajo y luego hacia algún lado (izquierda o derecha)

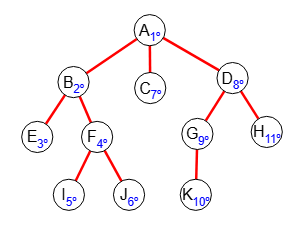
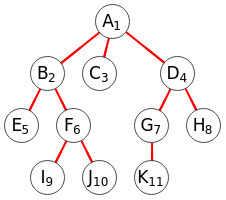
Este algoritmo puede aplicarse a cualquier grafo, pero es en el árbol, que es un grafo conexo sin ciclos, donde mejor se evidencia su funcionamiento. En la Figura puede ver un árbol donde hemos aplicado la búsqueda en profundidad, anotándose con un subíndice el número de orden de visita de los nodos. El nodo de inicio es el primero "A", viendo que empieza por la derecha del grafo primero bajando hasta la hoja "H" y luego continua a la izquierda y abajo hasta completar todo el recorrido.

La aplicación Grafos SVG devuelve además el siguiente resultado en forma de texto. En "visited" están los índices de los nodos visitados. En "path" está el camino con las aristas recorridas. Cuando los valores de los nodos no coinciden con sus índices, la aplicación ofrece las listas con esos valores.

Time: 0 ms

Búsqueda profundidad (Iterativo): {
"visited":[0,3,7,6,10,2,1,5,9,8,4],
"path":[[0,3],[3,7],[3,6],[6,10],[0,2],[0,1],[1,5],[5,9],[5,8],[1,4]]}

"visited": el índice del array es el orden de búsqueda, el valor del array es el índice del nodo; 
"path": cada subarray es una arista con dos índices de nodos

Valores nodos en orden de búsqueda desde el nodo "A" (index 0) ⇒ 
A, D, H, G, K, C, B, F, J, I, E

Camino con aristas valor nodo-valor nodo ⇒ 
A-D, D-H, D-G, G-K, A-C, A-B, B-F, F-J, F-I, B-E

Con este JSON se importa ese ejemplo.

{"nodes":[
    {"index":0,"nodeOffset":"10 -0.4","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"4.47 -4.6","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"10.2 -2.2","parent":[{"index":0}]},
    {"index":3,"nodeOffset":"18.2 -6.2","parent":[{"index":0}]},
    {"index":4,"nodeOffset":"-5.07 -7.6","parent":[{"index":1}]},
    {"index":5,"nodeOffset":"-1.09 -7.6","parent":[{"index":1}]},
    {"index":6,"nodeOffset":"19.1 -8.8","parent":[{"index":3}]},
    {"index":7,"nodeOffset":"26.89 -9.6","parent":[{"index":3}]},
    {"index":8,"nodeOffset":"2.6 -9.4","parent":[{"index":5}]},
    {"index":9,"nodeOffset":"1.71 -9.4","parent":[{"index":5}]},
    {"index":10,"nodeOffset":"3.47 -9.4","parent":[{"index":6}]}
],
"config":{
    "nodeValueAuto":"alphabetic-upper",
    "algorithm":"Depth first search (Iterative)"
}}

En la Figura vemos la opción invertir desactivada inicialmente, que en caso de activarse invierte el orden empezando en la parte izquierda del grafo y evolucionando hacia abajo primero y hacia la derecha:

Se obtiene este resultado:

Time: 0 ms

Búsqueda profundidad (Iterativo): {
"visited":[0,1,4,5,8,9,2,3,6,10,7],
"path":[[0,1],[1,4],[1,5],[5,8],[5,9],[0,2],[0,3],[3,6],[6,10],[3,7]]}

"visited": el índice del array es el orden de búsqueda, el valor del array es el índice del nodo;
"path": cada subarray es una arista con dos índices de nodos

Valores nodos en orden de búsqueda desde el nodo "A" (index 0) ⇒ 
A, B, E, F, I, J, C, D, G, K, H

Camino con aristas valor nodo-valor nodo ⇒ 
A-B, B-E, B-F, F-I, F-J, A-C, A-D, D-G, G-K, D-H

{"nodes":[
    {"index":0,"nodeOffset":"10 -0.4","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"4.47 -4.6","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"10.2 -2.2","parent":[{"index":0}]},
    {"index":3,"nodeOffset":"18.2 -6.2","parent":[{"index":0}]},
    {"index":4,"nodeOffset":"-5.07 -7.6","parent":[{"index":1}]},
    {"index":5,"nodeOffset":"-1.09 -7.6","parent":[{"index":1}]},
    {"index":6,"nodeOffset":"19.1 -8.8","parent":[{"index":3}]},
    {"index":7,"nodeOffset":"26.89 -9.6","parent":[{"index":3}]},
    {"index":8,"nodeOffset":"2.6 -9.4","parent":[{"index":5}]},
    {"index":9,"nodeOffset":"1.71 -9.4","parent":[{"index":5}]},
    {"index":10,"nodeOffset":"3.47 -9.4","parent":[{"index":6}]}
],
"config":{
    "nodeValueAuto":"alphabetic-upper",
    "algorithm":"Depth first search (Iterative)",
    "reverse":true
}}

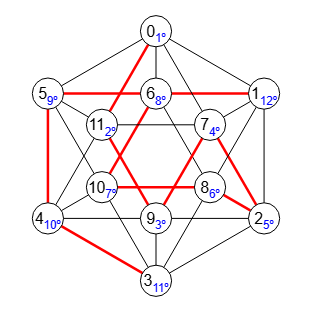
La búsqueda en profundidad se evidencia mejor sobre un árbol, pero puede aplicarse a cualquier grafo, como el de la Figura, un grafo Platónico icosaédrico que se puede obtener en la aplicación en la sección de generación.

Time: 0 ms

Búsqueda profundidad (Iterativo): {
"visited":[0,11,9,7,2,8,10,6,5,4,3,1],
"path":[[0,11],[11,9],[9,7],[7,2],[2,8],[8,10],[10,6],[6,5],[5,4],[4,3],[6,1]]}

"visited": el índice del array es el orden de búsqueda, el valor del array es el índice del nodo;
"path": cada subarray es una arista con dos índices de nodos

{"nodes":[
    {"index":0,"nodeOffset":"12.5","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"89.13","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"72.47 25","parent":[{"index":1}]},
    {"index":3,"nodeOffset":"29.17 25","parent":[{"index":2}]},
    {"index":4,"nodeOffset":"-14.13 -25","parent":[{"index":3}]},
    {"index":5,"nodeOffset":"-14.13","parent":[{"index":0},{"index":4}]},
    {"index":6,"nodeOffset":"12.5","parent":[{"index":0},{"index":1},{"index":5}]},
    {"index":7,"nodeOffset":"17.48 12.5","parent":[{"index":0},{"index":1},{"index":2}]},
    {"index":8,"nodeOffset":"17.48 12.5","parent":[{"index":1},{"index":2},{"index":3},{"index":6}]},
    {"index":9,"nodeOffset":"-4.17","parent":[{"index":2},{"index":3},{"index":4},{"index":7}]},
    {"index":10,"nodeOffset":"-25.82 -37.5","parent":[{"index":3},{"index":4},{"index":5},{"index":6},{"index":8}]},
    {"index":11,"nodeOffset":"-42.48 12.5","parent":[{"index":0},{"index":4},{"index":5},{"index":7},{"index":9}]}
],
"config":{
    "algorithm":"Depth first search (Iterative)"
}}

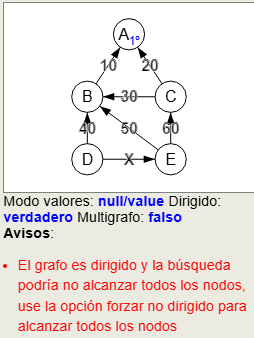
La búsqueda se inicia por defecto en el primer nodo, modificándose en el control primer índice nodo que podemos ver en la Figura. En la Figura vemos la búsqueda desde el primer nodo "A" en un grafo no dirigido, observando que no hay forma de acceder al resto del grafo. La aplicación advierte El grafo es dirigido y la búsqueda podría no alcanzar todos los nodos, use la opción forzar no dirigido para alcanzar todos los nodos.

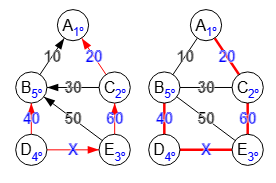
Usando la opción forzar no dirigido, la búsqueda ignora las direcciones de las aristas y trata el grafo como si fuera no dirigido, obteniéndose el grafo resaltado de la izquierda de la Figura. El resultado es el mismo que si convertimos el grafo en no dirigido y le aplicamos la misma búsqueda, como se observa en el grafo de la derecha.

DIRIGIDO

{"nodes":[
    {"index":0,"parent":[{"index":-1}]},
    {"index":1,"parent":[{"index":0,"value":10}]},
    {"index":2,"parent":[{"index":0,"value":20},{"index":1,"value":30}]},
    {"index":3,"parent":[{"index":1,"value":40},{"index":4,"value":"X"}]},
    {"index":4,"parent":[{"index":1,"value":50},{"index":2,"value":60}]}
],
"config":{
    "nodeValueAuto":"alphabetic-upper",
    "markerEnd":"arrow",
    "algorithm":"Depth first search (Iterative)",
    "forceUndirected":true
}}

NO DIRIGIDO

{"nodes":[
    {"index":0,"parent":[{"index":-1}]},
    {"index":1,"parent":[{"index":0,"value":10}]},
    {"index":2,"parent":[{"index":0,"value":20},{"index":1,"value":30}]},
    {"index":3,"parent":[{"index":1,"value":40},{"index":4,"value":"X"}]},
    {"index":4,"parent":[{"index":1,"value":50},{"index":2,"value":60}]}
],
"config":{
    "nodeValueAuto":"alphabetic-upper",
    "algorithm":"Depth first search (Iterative)"
}}

El código JavaScript para ejecutar getDepthFirstSearchIterative(). Usa getParents() para obtener los padres de un nodo y así seguir las aristas incidentes en cada nodo visitado.

function getDepthFirstSearchIterative({matrix=[], index=0, forceUndirected=false, 
    reverse=false}){
    let result = {visited: [], path: []};
    try {
        let stack = [];
        let k = -1;
        stack.push([index, k]);
        while (stack.length>0) {
            [index, k] = stack.pop();
            if (!result.visited.includes(index)){
                result.visited.push(index);
                if (k>-1) result.path.push([k, index]);
                let parents = getParents({matrix, index, forceUndirected});
                if (typeof parents==="string") throw new Error(parents);
                if (reverse) parents = parents.reverse();
                for (let j of parents) {
                    stack.push([j, index]);
                }
            }
        }
    } catch(e) {result = e.message}
    return result;
}

Búsqueda en profundidad en un grafo (recursivo) `getDepthFirstSearchRecursive()`

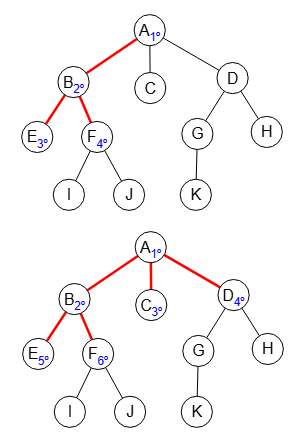
La versión recursiva del algoritmo de búsqueda en profundidad (DFS) recorre el grafo como la versión iterativa con la opción invertir activada, es decir, recorriendo el grafo hacia abajo y de izquierda a derecha, como se observa en la Figura.

Time: 0 ms

Búsqueda profundidad (Recursivo): {
"visited":[0,1,4,5,8,9,2,3,6,10,7],
"path":[[0,1],[1,4],[1,5],[5,8],[5,9],[0,2],[0,3],[3,6],[6,10],[3,7]]}

"visited": el índice del array es el orden de búsqueda, el valor del array es el índice del nodo;
"path": cada subarray es una arista con dos índices de nodos

Valores nodos en orden de búsqueda desde el nodo "A" (index 0) ⇒ 
A, B, E, F, I, J, C, D, G, K, H

Camino con aristas valor nodo-valor nodo ⇒ 
A-B, B-E, B-F, F-I, F-J, A-C, A-D, D-G, G-K, D-H

{"nodes":[
    {"index":0,"nodeOffset":"10 -0.4","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"4.47 -4.6","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"10.2 -2.2","parent":[{"index":0}]},
    {"index":3,"nodeOffset":"18.2 -6.2","parent":[{"index":0}]},
    {"index":4,"nodeOffset":"-5.07 -7.6","parent":[{"index":1}]},
    {"index":5,"nodeOffset":"-1.09 -7.6","parent":[{"index":1}]},
    {"index":6,"nodeOffset":"19.1 -8.8","parent":[{"index":3}]},
    {"index":7,"nodeOffset":"26.89 -9.6","parent":[{"index":3}]},
    {"index":8,"nodeOffset":"2.6 -9.4","parent":[{"index":5}]},
    {"index":9,"nodeOffset":"1.71 -9.4","parent":[{"index":5}]},
    {"index":10,"nodeOffset":"3.47 -9.4","parent":[{"index":6}]}
],
"config":{
    "nodeValueAuto":"alphabetic-upper",
    "algorithm":"Depth first search (Recursive)"
}}

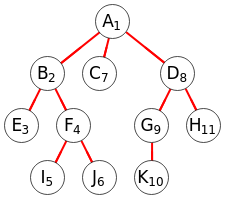
En la Figura vemos como exportamos a Wolfram esta versión recursiva, agregándose también los subíndices que indican el orden de visita a los nodos.

Usamos DepthFirstScan para recorrer en DFS el grafo, usando el argumento "FrontierEdge" como evento para actuar cuando encuentra una arista, pues queremos obtener una lista de aristas en d = Part[e[[2]], 1] recorridas para luego resaltarlas con HighlightGraph.

El siguiente paso es agregar los subíndices de orden de visita. Wolfram es un lenguaje potente pero bastante complejo y yo estoy empezando a conocerlo. La verdad no ha sido fácil incluir estos subíndices. Después de algunas vueltas lo he conseguido con las variables m y x, obteniendo en esta última la lista {A,B,C,D,E,F,G,H,I,J,K} con los valores de los nodos. Usando esta lista construimos la lista de etiquetas de nodos l con el contenido {1->Placed[A₁, Center], 2->Placed[B₂, Center], ...} que nos servirá para la última línea Graph[h, VertexLabels->l] que, finalmente, mostrará el grafo con aristas resaltadas y con subíndices en las etiquetas de los vértices.

g = AdjacencyGraph[{{0,1,1,1,0,0,0,0,0,0,0},{1,0,0,0,1,1,0,0,0,0,0},{1,0,0,0,0,0,0,0,0,0,0},{1,0,0,0,0,0,1,1,0,0,0},{0,1,0,0,0,0,0,0,0,0,0},{0,1,0,0,0,0,0,0,1,1,0},{0,0,0,1,0,0,0,0,0,0,1},{0,0,0,1,0,0,0,0,0,0,0},{0,0,0,0,0,1,0,0,0,0,0},{0,0,0,0,0,1,0,0,0,0,0},{0,0,0,0,0,0,1,0,0,0,0}}, ImageSize->226, VertexSize->{"Scaled", 0.14}, VertexLabels->{1->Placed["A",Center], 2->Placed["B",Center], 3->Placed["C",Center], 4->Placed["D",Center], 5->Placed["E",Center], 6->Placed["F",Center], 7->Placed["G",Center], 8->Placed["H",Center], 9->Placed["I",Center], 10->Placed["J",Center], 11->Placed["K",Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
m = SortBy[MapApply[List, AnnotationValue[g, VertexLabels]], 1];
x = Table[m[[i]][[2]][[1]],{i, Length[m]}];
e = Reap[DepthFirstScan[g, 1, {"FrontierEdge"->Sow}]];
d = Part[e[[2]], 1];
v = VertexList[d];
l = Table[v[[i]]->Placed[Subscript[x[[v[[i]]]],i], Center], {i, Length[v]}];
h = HighlightGraph[g, {Style[d, Red, Thick], Annotation[d, EdgeLabelStyle->Directive[Blue,17.5,Bold]]}];
Graph[h, VertexLabels->l]

El código JavaScript para ejecutar getDepthFirstSearchRecursive() es el siguiente, que usa getParents() para obtener los padres de un nodo y así seguir las aristas incidentes en cada nodo visitado.

function getDepthFirstSearchRecursive({matrix=[], index=0, forceUndirected=false, 
    reverse=false, result={visited:[], path:[]}}){
    if (iter++, iter>maxIter) return `Maximum iterations '${maxIter}' reached`;
    try {
        result.visited.push(index);
        let parents = getParents({matrix, index, forceUndirected});
        if (typeof parents==="string") throw new Error(parents);
        if (reverse) parents = parents.reverse();
        for (let j of parents) {
            if (!result.visited.includes(j)){
                result.path.push([index, j]);
                let temp = getDepthFirstSearchRecursive({matrix, index:j, forceUndirected, result});
                if (typeof temp==="string") throw new Error(temp);
            }
        }
    } catch(e) {result = e.message}
    return result;
}

Búsqueda en anchura en un grafo (iterativo) `getBreadthFirstSearchIterative()`

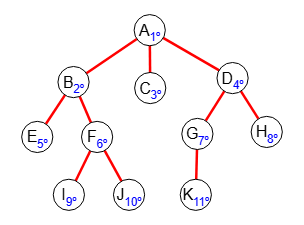
El algoritmo de búsqueda primero en anchura, en inglés Breadth-first search y su abreviatura BFS, recorre el grafo empezando en un nodo que se indique atravesando los nodos primero hacia hacia algún lado (izquierda o derecha) y luego hacia abajo.

En la Figura vemos que primero busca hacia la derecha y luego hacia abajo. La aplicación devuelve el resultado siguiente:

Time: 1 ms

Búsqueda en anchura (Iterativo): {
"visited":[0,1,2,3,4,5,6,7,8,9,10],
"path":[[0,1],[0,2],[0,3],[1,4],[1,5],[3,6],[3,7],[5,8],[5,9],[6,10]]}

"visited": el índice del array es el orden de búsqueda, el valor del array es el índice del nodo;
"path": cada subarray es una arista con dos índices de nodos

Valores nodos en orden de búsqueda desde el nodo "A" (index 0) ⇒ 
A, B, C, D, E, F, G, H, I, J, K

Camino con aristas valor nodo-valor nodo ⇒ 
A-B, A-C, A-D, B-E, B-F, D-G, D-H, F-I, F-J, G-K

{"nodes":[
    {"index":0,"nodeOffset":"10 -0.4","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"4.47 -4.6","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"10.2 -2.2","parent":[{"index":0}]},
    {"index":3,"nodeOffset":"18.2 -6.2","parent":[{"index":0}]},
    {"index":4,"nodeOffset":"-5.07 -7.6","parent":[{"index":1}]},
    {"index":5,"nodeOffset":"-1.09 -7.6","parent":[{"index":1}]},
    {"index":6,"nodeOffset":"19.1 -8.8","parent":[{"index":3}]},
    {"index":7,"nodeOffset":"26.89 -9.6","parent":[{"index":3}]},
    {"index":8,"nodeOffset":"2.6 -9.4","parent":[{"index":5}]},
    {"index":9,"nodeOffset":"1.71 -9.4","parent":[{"index":5}]},
    {"index":10,"nodeOffset":"3.47 -9.4","parent":[{"index":6}]}
],
"config":{
    "nodeValueAuto":"alphabetic-upper",
    "algorithm":"Breadth first search (Iterative)"
}}

El resultado en Wolfram se observa en la Figura usando BreadthFirstScan. El resto del código es como el que mostramos en el apartado anterior, pudiendo consultar allí los comentarios que expusimos.

g = AdjacencyGraph[{{0,1,1,1,0,0,0,0,0,0,0},{1,0,0,0,1,1,0,0,0,0,0},{1,0,0,0,0,0,0,0,0,0,0},{1,0,0,0,0,0,1,1,0,0,0},{0,1,0,0,0,0,0,0,0,0,0},{0,1,0,0,0,0,0,0,1,1,0},{0,0,0,1,0,0,0,0,0,0,1},{0,0,0,1,0,0,0,0,0,0,0},{0,0,0,0,0,1,0,0,0,0,0},{0,0,0,0,0,1,0,0,0,0,0},{0,0,0,0,0,0,1,0,0,0,0}}, ImageSize->226, VertexSize->{"Scaled", 0.14}, VertexLabels->{1->Placed["A",Center], 2->Placed["B",Center], 3->Placed["C",Center], 4->Placed["D",Center], 5->Placed["E",Center], 6->Placed["F",Center], 7->Placed["G",Center], 8->Placed["H",Center], 9->Placed["I",Center], 10->Placed["J",Center], 11->Placed["K",Center]}, VertexLabelStyle->Directive[Black,17.5], EdgeLabelStyle->Directive[Black,17.5,Bold], VertexStyle->White, EdgeStyle->{{Black,Thickness[0.005]}}];
m = SortBy[MapApply[List, AnnotationValue[g, VertexLabels]], 1];
x = Table[m[[i]][[2]][[1]],{i, Length[m]}];
e = Reap[BreadthFirstScan[g, 1, {"FrontierEdge"->Sow}]];
d = Part[e[[2]], 1];
v = VertexList[d];
l = Table[v[[i]]->Placed[Subscript[x[[v[[i]]]],i], Center], {i, Length[v]}];
h = HighlightGraph[g, {Style[d, Red, Thick], Annotation[d, EdgeLabelStyle->Directive[Blue,17.5,Bold]]}];
Graph[h, VertexLabels->l]

El código JavaScript para ejecutar getBreadthFirstSearchRecursive() es el siguiente, que usa getParents() para obtener los padres de un nodo y así seguir las aristas incidentes en cada nodo visitado.

function getBreadthFirstSearchIterative({matrix=[], index=0, forceUndirected=false, 
    reverse=false}){
    let result = {visited:[], path:[]};
    try {
        let queue = [];
        queue.push(index);
        result.visited.push(index);
        while (queue.length>0) {
            index = queue.shift();
            let parents = getParents({matrix, index, forceUndirected});
            if (typeof parents==="string") throw new Error(parents);
            if (reverse) parents = parents.reverse();
            for (let j of parents) {
                if (!result.visited.includes(j)){
                    result.visited.push(j);
                    result.path.push([index, j]);
                    queue.push(j);
                }
            }
        }
    } catch(e) {result = e.message}
    return result;
}

Obtener subárboles `getSubtrees()`

Mejora agregada el 23 may 2026 a la aplicación Grafos SVG

Con DFS o BFS obtenemos un árbol. Podríamos pensar en un árbol como un tronco que parte desde un nodo raíz encadenando linealmente uno o más nodos y luego cero o más ramas que parten desde nodos en ese tronco. Las ramas vendrían a ser como subárboles, pues a su vez podríamos identificar un subtronco con subramas. Y así indefinidamente de forma recursiva.

Definiendo un nodo como raíz, con el algoritmo getSubtrees() obtenemos el árbol usando DFS o BFS, identificando las hojas del árbol y a continuación buscamos en ese árbol el primer camino más largo entre el nodo raíz y cada una de los nodos hoja con el algoritmo findPath(). Este camino más largo será el tronco (con aristas en color rojo). Luego identificamos las ramas entre el resto de caminos (aristas y nodos en color verde).

Para el grafo de la Figura obtenemos el siguiente resultado con getSubtrees() usando DFS y con nodo raíz el "0":

Time: 1 ms
Obtener subárboles: {
"visited":[0,10,11,12,9,4,7,6,8,5,2,3,1],
"path":[[0,10],[10,11],[11,12],[12,9],[0,4],[4,7],[4,6],[6,8],[6,5],[5,2],[2,3],[2,1]],
"root":0,
"leaves":[9,8,7,3,1],
"pathsFromRoot":[[0,10,11,12,9],[0,4,6,8],[0,4,7],[0,4,6,5,2,3],[0,4,6,5,2,1]],
"trunk":[0,4,6,5,2,3],
"branches":[[0,10,11,12,9],[6,8],[4,7],[2,1]]}

En "visited" y "path" obtenemos el resultado del DFS en este caso, representando el árbol en la Figura usando la lista de aristas de "path", ubicando la raíz "0" en la parte baja de la imagen.

Obtenemos todos los caminos desde la raíz a las hojas ("leaves" [9,8,7,3,1]) que devolvemos en "pathsFromRoot". El primero más largo es el que llega al nodo "3" con una longitud de 6 nodos, con lo que este camino será el tronco del árbol que guardamos en "trunk" [0,4,6,5,2,3]. Luego con el resto de caminos de "pathsFromRoot" identificamos las ramas "branches" [[0,10,11,12,9],[6,8],[4,7],[2,1]], donde el primer nodo de cada rama es un nodo del tronco.

En la Figura vemos las opciones para ejecutar el algoritmo getSubtrees(). Indicamos el nodo raíz en el campo primer índice nodo. Usará DFS iterativo por defecto a no ser que se active anchura en cuyo caso usará BFS (que también es iterativo). El campo inverso se aplica a esas búsquedas DFS o BFS. Podemos forzar a no dirigido el grafo.

Los otros campos no forman parte del algoritmo y sólo sirven para dotar de color tras la ejecución. Con color camino damos color al tronco y con color camino 2 a la ramas. El color fondo nodo se aplica a los nodos de las ramas. El color texto es para los subíndices de orden de visita del DFS o BFS.

Con el grafo de Petersen de la Figura usando la raíz "0" obtenemos un tronco con 9 nodos y una rama con 1 nodo. Lo mismo sucede con cualquiera de los otros nodos exteriores 1, 2, 3, o 4, pues con los interiores 5, 6, 7, 8, y 9 se obtiene un tronco con todos los nodos y sin ramas, como vemos en la Figura para la raíz "5". De hecho este es uno de los caminos Hamiltonianos existentes entre los nodos "1" y "5" en el grafo de Petersen. No todos los grafos tiene un camino Hamiltoniano, como es el caso del grafo de la Figura.

Las ramas son también árboles, lo que entendemos como subárboles del grafo, en algún caso con subramas, como el superior que involucra los nodos 6, 5, 2, 3 y 1 del grafo de la Figura, obtenido con getSubtrees() con DFS y raíz "0". Como dijimos al principio, los subtroncos y subramas de los subárboles pueden descubrirse de forma recursiva, pero con este algoritmo getSubtrees() no lo hacemos así, pues complicaría mucho la ejecución.

Lo que hacemos es descubrir el tronco [0,4,6,8,12,11,10,9] y las ramas [4,7], [6,5,2,3] y [6,5,2,1], observando que las dos últimas componen un subárbol con el subtronco [6,5,2] y las subramas [2,1] y [2,3] aunque no se especifican en el resultado de getSubtrees() que es el siguiente.

Obtener subárboles: {
"visited":[0,4,7,6,8,12,11,10,9,5,2,3,1],
"path":[[0,4],[4,7],[4,6],[6,8],[8,12],[12,11],[11,10],[10,9],[6,5],[5,2],[2,3],2,1]],
"root":0,
"leaves":[9,7,3,1],
"pathsFromRoot":[[0,4,6,8,12,11,10,9],[0,4,7],[0,4,6,5,2,3],[0,4,6,5,2,1]],
"trunk":[0,4,6,8,12,11,10,9],
"branches":[[4,7],[6,5,2,3],[6,5,2,1]],
"warnings":[]}

El algoritmo getSubtrees() se aplica solo a grafos conectados. Si en el grafo de la Figura eliminamos la arista 6-8 tendremos dos componentes conectados, devolviendo getSubtrees() el error El grafo es desconectado y este algoritmo es sólo para grafos conectados.

Con el grafo de la Figura aplicando getSubtrees() usando BFS desde raíz "0" vemos que se obtienen 3 ramas, donde dos de ellas son subárboles con dos subramas. Si hubiésemos usado DFS tendríamos todos los nodos en un único tronco sin ramas, pues existe un camino Hamiltoniano entre los nodos "1" y "0" como vemos en la Figura.

Un DFS o BFS puede obtenerse también en un grafo dirigido, aunque puede que no alcance a todos los nodos. En el grafo de la Figura vemos los subárboles obtenidos con raíz nodo "2" usando BFS, observando que no se alcanza el nodo "3", algo que puede evitarse forzando a no dirigido tal como vemos en la Figura.

En el primer caso vemos a continuación el resultado de getSubtrees(), observando el aviso de que el grafo es dirigido y que la búsqueda podría no alcanzar todos los nodos, proponiéndose usar la opción forzar no dirigido para alcanzar todos los nodos.

Time: 1 ms
Obtener subárboles: 
{"visited":[2,0,1,4],
"path":[[2,0],[2,1],[0,4],[4,-1]],
"root":2,
"leaves":[4,3,1],
"pathsFromRoot":[[2,0,4],[2,1]],
"trunk":[2,0,4],
"branches":[[2,1]],
"warnings":["The graph is directed and the search may not reach all nodes,
use the force undirected option to reach all nodes"]}

En el JavaScript de getSubtrees() que vemos a continuación se usan los siguientes algoritmos:

isGraphDirected para saber si el grafo es dirigido.
getDepthFirstSearchIterative para búsqueda en profundidad iterativa (DFS).
getBreadthFirstSearchIterative para búsqueda en anchura iterativa (BFS).
convertToAdjacencyMatrix para convertir una lista de aristas en matriz de adyacencia.
findPath para encontrar un camino entre dos nodos.

Recuerde que los algoritmos no incluyen el coloreado para diferenciar las partes del resultado, algo que hacemos posteriormente en la aplicación a partir del resultado obtenido.

function getSubtrees({matrix=[], index=0, reverse=false, forceUndirected=false, breadth=false}){
    let result = {visited:[], path:[], root:index, leaves: [], pathsFromRoot: [], trunk:[], branches:[], warnings:[]}, temp;
    try {
        let n = matrix.length;
        let compactUndirected = false;
        if (forceUndirected) {
            compactUndirected = true;
        } else {
            if (temp = isGraphDirected({matrix}), temp.error) throw new Error(temp.error);
            compactUndirected = !temp;
        }
        let method = breadth ? getBreadthFirstSearchIterative : getDepthFirstSearchIterative;
        if (temp = method({matrix, index, reverse, forceUndirected}), temp.error) throw new Error(temp.error);
        result.visited = temp.visited;
        if (result.visited.length < n) result.warnings.push(`The graph is directed and the search may not reach all nodes, use the force undirected option to reach all nodes`);
        result.path = temp.path;
        if (result.path.length===0) throw new Error(`There is no tree '${breadth?"BFS":"DFS"}' from the root '${index}'`);
        result.leaves = []; 
        for (let i=0; i<n; i++){
            let f = result.path.filter(v => v[0]===i);
            if (f.length===0) result.leaves.push(i);
        }
        if (temp = convertToAdjacencyMatrix({array:result.path, mode:"edgeList", compactUndirected}), temp.error) throw new Error(temp.error);
        let matrixPath = temp;
        let [iTrunk, len] = [-1, 0];
        if (!reverse) result.leaves.reverse();
        for (let i of result.leaves){
            if (temp = findPath({matrix:matrixPath, firstIndex:index, lastIndex:i}), temp.error) throw new Error(temp.error);
            if (temp.length>0) {
                let nodes = temp[0];
                result.pathsFromRoot.push(nodes);
                if (nodes.length>len) [iTrunk, len] = [result.pathsFromRoot.length-1, nodes.length];
            }
        }
        if (iTrunk>-1) {
            result.trunk = result.pathsFromRoot[iTrunk];
            for (let i=0; i<result.pathsFromRoot.length; i++) {
                if (i!==iTrunk) {
                    let nodes = result.pathsFromRoot[i];
                    let rootBranch = -1;
                    let j = -1;
                    for (j=0; j<nodes.length; j++) {
                        if (nodes[j]===result.trunk[j]) {
                            rootBranch = j;
                        } else {
                            j--;
                            break;
                        }
                    }
                    if (j>-1) nodes = nodes.slice(j);
                    result.branches.push(nodes);
                }
            }
        }
    } catch(e) {result = e.message}
    return result;
}

Búsqueda en un grafo `searchInGraph()`

Los algoritmos vistos de búsqueda en profundidad o anchura contienen el término búsqueda, search en inglés. Pero realmente no buscan nada, pues lo que hacen es explorar todos los nodos del grafo. El nombre que usa Wolfram DepthFirstScan y BreadthFirstScan usa el término scan precisamente con el significado de explorar.

He mantenido el término búsqueda (search) en los nombres de los algoritmos getDepthFirstSearchIterative(), getDepthFirstSearchRecursive() y getBreadthFirstSearchIterative() para evitar confusiones con las abreviaturas DFS y BFS, donde la "S" es conocida por significar "Search", pero para ser coherentes debería poner "Scan", pues la "S" en "BFS" y "DFS" también podrían referirse a "Scan" en lugar de a "Search".

Por supuesto que esos algoritmos nos pueden servir para buscar algo en el grafo. Y esto es lo que hacemos con el algoritmo searchInGraph(), que verdaderamente busca un nodo o una arista que le indiquemos. En la Figura vemos una búsqueda del nodo "F" usando DFS y BFS.

Este es el resultado de la búsqueda del nodo con valor "F" en profundidad (DFS). con la opción invertir activada para que empiece en la parte izquierda del árbol. En matchNode devolverá la coincidiencia encontrada [5, "F"] con el índice y valor del nodo buscado.

Time: 0 ms

Buscar en el grafo: {
"matchNode":[5,"F"],
"matchEdge":[],
"visited":[0,1,4,5],
"path":[[0,1],[1,4],[1,5]]}

"visited": el índice del array es el orden de búsqueda, el valor del array es el índice del nodo;
"path": cada subarray es una arista con dos índices de nodos

Valores nodos en orden de búsqueda desde el nodo "A" (index 0) ⇒ 
A, B, E, F

Camino con aristas valor nodo-valor nodo ⇒ 
A-B, B-E, B-F

Y este es el resultado para la búsqueda en anchura (BFS):

Time: 0 ms

Buscar en el grafo: {
"matchNode":[5,"F"],
"matchEdge":[],
"visited":[0,1,2,3,4,5],
"path":[[0,1],[0,2],[0,3],[1,4],[1,5]]}

"visited": el índice del array es el orden de búsqueda, el valor del array es el índice del nodo;
"path": cada subarray es una arista con dos índices de nodos

Valores nodos en orden de búsqueda desde el nodo "A" (index 0) ⇒ 
A, B, C, D, E, F

Camino con aristas valor nodo-valor nodo ⇒ 
A-B, A-C, A-D, B-E, B-F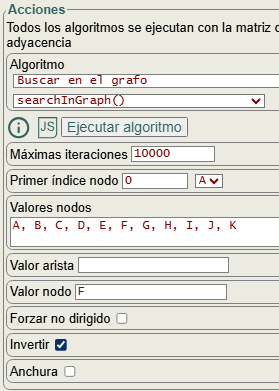

En la Figura vemos las opciones para buscar el nodo con valor "F" en el grafo. Todos los algoritmos se ejecutan sobre la matriz de adyacencia. Y ésta puede portar los valores de las aristas, pero no los valores de los nodos. Por lo tanto es necesario pasar una lista de valores de nodos, algo que la aplicación hace automáticamente.

En valor nodo pondremos un valor de la lista de nodos a buscar. Y en valor arista un valor de arista. Si se ponen los dos devolverá lo lo primero que encuentre.

La opción anchura desactivada busca con DFS y activada con BFS. La opción invertir invierte la dirección horizontal de búsqueda, como ya vimos en ejemplos anteriores. Así como forzar no dirigido para aplicar a los grafos dirigidos, con un ejemplo que vimos en el primer apartado.

Puede importar el ejemplo con este JSON, con la propiedad "breadth":false, "reverse":true para el DFS breadth":true, "reverse":false para el BFS:

{"nodes":[
    {"index":0,"nodeOffset":"10 -0.4","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"4.47 -4.6","parent":[{"index":0}]},
    {"index":2,"nodeOffset":"10.2 -2.2","parent":[{"index":0}]},
    {"index":3,"nodeOffset":"18.2 -6.2","parent":[{"index":0}]},
    {"index":4,"nodeOffset":"-5.07 -7.6","parent":[{"index":1}]},
    {"index":5,"nodeOffset":"-1.09 -7.6","parent":[{"index":1}]},
    {"index":6,"nodeOffset":"19.1 -8.8","parent":[{"index":3}]},
    {"index":7,"nodeOffset":"26.89 -9.6","parent":[{"index":3}]},
    {"index":8,"nodeOffset":"2.6 -9.4","parent":[{"index":5}]},
    {"index":9,"nodeOffset":"1.71 -9.4","parent":[{"index":5}]},
    {"index":10,"nodeOffset":"3.47 -9.4","parent":[{"index":6}]}
],
"config":{
    "nodeValueAuto":"alphabetic-upper",
    "algorithm":"Search in graph",
    "nodeValues":"A, B, C, D, E, F, G, H, I, J, K",
    "targetNodeValue":"F",
    "breadth":false,
    "reverse":true
}}

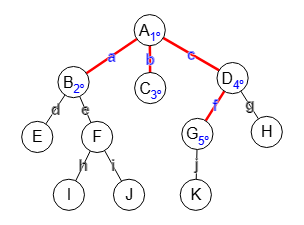
En la Figura vemos la búsqueda de la arita "f" con BFS. Al llegar al nodo "D" consulta todas sus aristas incidentes, si alguna de ellas coincide con la búsqueda finaliza devolviendo ese recorrido incluyendo el nodo siguiente "G" de esa arista "f".

{"nodes":[
    {"index":0,"nodeOffset":"10 -0.4","parent":[{"index":-1}]},
    {"index":1,"nodeOffset":"4.47 -4.6","parent":[{"index":0,"value":"a"}]},
    {"index":2,"nodeOffset":"10.2 -2.2","parent":[{"index":0,"value":"b"}]},
    {"index":3,"nodeOffset":"18.2 -6.2","parent":[{"index":0,"value":"c"}]},
    {"index":4,"nodeOffset":"-5.07 -7.6","parent":[{"index":1,"value":"d"}]},
    {"index":5,"nodeOffset":"-1.09 -7.6","parent":[{"index":1,"value":"e"}]},
    {"index":6,"nodeOffset":"19.1 -8.8","parent":[{"index":3,"value":"f"}]},
    {"index":7,"nodeOffset":"26.89 -9.6","parent":[{"index":3,"value":"g"}]},
    {"index":8,"nodeOffset":"2.6 -9.4","parent":[{"index":5,"value":"h"}]},
    {"index":9,"nodeOffset":"1.71 -9.4","parent":[{"index":5,"value":"i"}]},
    {"index":10,"nodeOffset":"3.47 -9.4","parent":[{"index":6,"value":"j"}]}
],
"config":{
    "nodeValueAuto":"alphabetic-upper",
    "algorithm":"Search in graph",
    "nodeValues":"A, B, C, D, E, F, G, H, I, J, K",
    "targetEdgeValue":"f",
    "breadth":true
}}

function searchInGraph({matrix=[], index=0, breadth=false, reverse=false, forceUndirected=false, 
    nodeValues=[], targetNodeValue="", targetEdgeValue="", valueNull=targetEdgeValue==="" ? 0 : null, 
    indexSearch=nodeValues.indexOf(targetNodeValue)}){
    let result = {matchNode:[], matchEdge:[], visited:[], path:[]};
    try {
        let stackQueue = [];
        let k = -1;
        stackQueue.push([index, k]);
        while (stackQueue.length>0) {
            [index, k] = breadth ? stackQueue.shift() : stackQueue.pop();
            if (!result.visited.includes(index)){
                result.visited.push(index);
                if (k>-1) result.path.push([k, index]);
                if (index===indexSearch) {
                    result.matchNode = [indexSearch, targetNodeValue];
                    return result;
                }
                let parents = getParents({matrix, index, forceUndirected, valueNull});
                if (typeof parents==="string") throw new Error(parents);
                if (reverse) parents = parents.reverse();
                for (let j of parents) {
                    if (matrix[index][j]!==null && matrix[index][j].toString()===targetEdgeValue || 
                    forceUndirected && matrix[j][index]!==null && matrix[j][index].toString()===targetEdgeValue) {
                        result.visited.push(j);
                        result.path.push([index, j]);
                        result.matchEdge = [index, j, targetEdgeValue];
                        return result;
                    }
                    stackQueue.push([j, index]);
                }
            }
        }
    } catch(e) {result = e.message}
    return result;
}

Búsqueda en profundidad en un grafo (iterativo) getDepthFirstSearchIterative()

Búsqueda en profundidad en un grafo (recursivo) getDepthFirstSearchRecursive()

Búsqueda en anchura en un grafo (iterativo) getBreadthFirstSearchIterative()

Obtener subárboles getSubtrees()

Búsqueda en un grafo searchInGraph()

Búsqueda en profundidad en un grafo (iterativo) `getDepthFirstSearchIterative()`

Búsqueda en profundidad en un grafo (recursivo) `getDepthFirstSearchRecursive()`

Búsqueda en anchura en un grafo (iterativo) `getBreadthFirstSearchIterative()`

Obtener subárboles `getSubtrees()`

Búsqueda en un grafo `searchInGraph()`