Usando el Trazador de Gráficas para practicar con fractales

Muestras de fractales

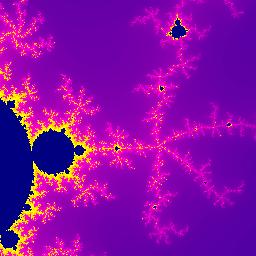Imagen no disponible

Conjunto de Mandelbrot. Una muestra de hasta donde podemos llegar con el trazador de gráficas matemáticas para generar fractales.

El tema anterior me sirvió como primer acercamiento al aspecto de programación de los fractales, pero para seguir profundizando necesitaba no tener que estar escribiendo todo el script cada vez que quería poner en práctica un ejemplo. Tras hacer algunas mejoras y adaptaciones al trazador de gráficas matemáticas, pude finalmente hacer algunos ejemplos como los que aparecen a la izquierda. La generación de fractales del tema anterior la podíamos llevar a cabo aplicando un sistema de funciones iteradas, o lo que es lo mismo, aplicando homotecias a las formas iniciales. Para esto aplicábamos algoritmos recursivos. También podíamos generarlos aplicando una selección aleatoria de puntos con lo cual ya no necesitábamos el recursivo, pero teníamos que fijar un número máximo de puntos para el bucle iterador. Con el trazador de gráficas no podemos hacer uso de la técnica recursiva, sólo podemos usar la iterativa. La selección puede realizarse por el método aleatorio, como antes, pero también verificando todos los puntos del plano, uno a uno, para ver si formarán parte del conjunto fractal o son desechados. Es lo que podemos llamar un algoritmo iterativo de selección de puntos.

En el conjunto de imagenes de la izquierda se muestran algunas capturas de fractales realizados con ese trazador de gráficas matemáticas. La primera es un Conjunto de Mandelbrot. Hay también una muestra de un Conjunto de Julia, Triángulo y Alfombra de Sierpinski y otros ejemplos. Aunque este trazador permite generar fractales, sin embargo no es una aplicación destinada a ello. En el tema siguiente Generador de fractales iterativos he realizado una aplicación para construir fractales mediante algoritmos iterativos de selección de puntos. La ventaja es que es más rápido que el trazador de gráficas pudiéndose generar imágenes de mayor tamaño en menos tiempo, aparte de un conjunto de facilidades para configurar la presentación del fractal. Por el momento en este tema voy a explicar un poco como codificar un fractal en el trazador de gráficas y como hacer un algoritmo iterativo de selección de puntos.

Generando fractales con un algoritmo iterativo de selección de puntos

Podemos definir este algoritmo iterativo de selección de puntos en pseudo-código como sigue:

Declarar plano XY [x1,x2]×[y1,y2]
Bucle x=x1 hasta x=x2
    Bucle y=y1 hasta y=y2
        Bucle seleccionador de puntos
            Si (x,y) cumple la condición de selección
                Salir de este bucle
            Fin si
        Fin bucle
        Si completamos este bucle
            Pintar punto (x,y)
        Fin si        
    Fin bucle
Fin bucle

En el siguiente ejemplo hay un <canvas> con un script muy básico para generar el Conjunto de Julia aplicando el anterior algoritmo:

El HTML contiene el elemento <canvas> identificado con id="canvasFractal" y medidas 200×200 píxeles. A continuación está el JavaScript siguiente:

<script>
    var canvasFractal = document.getElementById("canvasFractal");
    var contexto = null;
    if (canvasFractal.getContext) contexto = canvasFractal.getContext("2d");
    function ejecutarFractal(){
        if (contexto){
            contexto.clearRect(0,0,canvasFractal.width,canvasFractal.height);
            contexto.fillStyle = "black";
            var ancho = canvasFractal.width;
            var alto = canvasFractal.height;
            var escape = 30;
            var a = -0.75;
            var b = 0;
            for (var i=0; i<=canvasFractal.width; i++){
                for (var j=0; j<=canvasFractal.height; j++){
                    x = (i-ancho/2)/50;
                    y = -(j-ancho/2)/50;
                    for(var k=0; k<escape; k++){
                        var m = Math.pow(x,2);
                        var n = Math.pow(y,2);
                        if ((m+n)>4) break;
                        var p = m-n+a;
                        var q = 2*x*y+b;
                        x = p;
                        y = q;
                     }
                    if (k==escape) contexto.fillRect(i,j,1,1);
                }
            }
        }
    }
</script>

La función ejecutarFractal() se ejecuta en el window.onload de esta página. Se observa que se sigue la estructura de bucles mencionada ante. Para este particular ejemplo de los Conjuntos de Julia la condición de selección es (m+n)>4 (esto se explica en un apartado más abajo). Lo interesante es ver que vamos iterando por todos los puntos del plano de 200×200 píxeles. Convertimos esos píxeles en unidades (x,y) absolutas de un plano [-2,2]×[-2,2]. Luego pasamos cada punto (x,y) al bucle seleccionador. Finalmente si k==escape es que el punto no fue seleccionado y por tanto escapó de esa condición. Estos son los puntos que se pintan en negro y los que pertenecen al fractal. El resto no se pintan en este ejemplo, aunque también podríamos darle un color diferenciado.

La Alfombra de Sierpinski con el Trazador de Gráficas Matemáticas

La Alfombra Sierpinski es un fractal que ya generamos en el tema anterior usando un sistema de funciones iteradas. Este de la imagen, que originalmente es de 243×243 píxeles, lo generé con el trazador de gráficas matemáticas. Pero ahora usando un algoritmo iterativo de selección de puntos. Esa aplicación permite codificar en JavaScript lo necesario para representar una función matemática. Ahora se trata de usar ese recurso para implementar el algoritmo que seleccione los puntos del plano y decidir si pertenecen o no al fractal. La configuración de una función en el trazador se puede exportar a texto. La de ese fractal es la siguiente:

edita-funcion:
i=0..242;
j=0..242;
r=i;
s=j;
f=1;
while((r>0)||(s>0)){
    if ((r%3==1)&&(s%3==1)) {
        f=0;
        break;
    }
    r = floor(r/3);
    s = floor(s/3);
}
if (f==1){
    x=i;
    y=j;
}
_anchoxy:243_altoxy:243_zoomx:1_zoomy:1
_remarcar:0_precision:1_ejes:0_subejes:0
_graduacion:0_contorno:0_usar-colores:1
_movex:-121.5_movey:121.5_trazar-lineas:0

Los distintos campos de configuración están separados por el carácter "_". El campo edita-funcion contiene el código JavaScript para la generación de la función (en color azul). Bueno, casi todo es JavaScript, pues lo resaltado en amarillo es una construcción específica para el trazador. Se trata de declarar un rango de iteración. Recuerde que en el trazador sólo podemos declarar variables nombradas como una única letra del conjunto a..z. Las variables i,j se declaran para que iteren por un plano de 243×243 unidades. En cada bucle se tomará un punto de ese plano, cuyas coordenadas se traspasan a las variables r,s.

Ahora hay que decidir si ese punto (r,s) = (i,j) del plano pertenece o no al fractal que estamos buscando. Para ello usamos un bucle while que toma los valores r,s enteros y aplica la división entera hasta que el cociente de alguno de ellos sea cero. Usamos la función de JavaScript Math.floor() para este cometido. Por defecto cuando entramos en el bucle while suponemos que el punto (i,j) pertenece al fractal (para eso ponemos f=1). Cuando el resto de esa división entera sea 1 para ambas coordenadas, sabremos que ese punto (i,j) NO pertenece al fractal y saldremos del bucle (ponemos f=0). Si f==1 es que el punto escapó, es decir, pasó todo el bucle while sin que se cortara y por lo tanto pertenece al fractal y lo pintamos. En el trazador esto equivale a darle un valor a la pareja de coordenadas (x,y) que son las variables que se pintan finalmente. En definitiva, si la expresión booleana (r%3==1)&&(s%3==1) es verdadera entonces el punto (r,s) no pertenece al fractal. Estos puntos son las zonas blancas que no se pintan. Se trata de comprobar que el resto de la división nos de 1 con ambas coordenadas. ¿Porqué esto es así?.

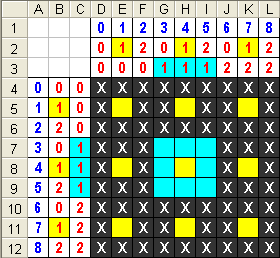La imagen de la izquierda es también de una Alfombra de Sierpinski, cuyo original de 728×728 píxeles lo he generado en una hoja de cálculo de Excel. También es posible usarlo para generar estos fractales sencillos. En la imagen de la derecha puede ver un trozo de ese hoja correspondiente a un cuadro de 9×9 puntos. La columna y fila con números en azul son los puntos (r,s) que estamos evaluando en el plano. En rojo aparecen las iteraciones para determinar el resto de la división. Así cuando en una intersección el resto es 1 en ambas coordenadas entonces NO pintamos una "X" en ese punto. Por ejemplo, el punto (1,5) si pertenece al fractal, pues 1%3=1 y 5%3=2≠1 (donde % es la operación resto de la división). No necesitamos hacer una segunda iteración pues la primera división entera 1/3=0 y ya no cabe seguir comprobando. En cambio el punto (4,7) no pertenece, pues 4%3=1 y 7%3=1, esto con la primera iteración. Tampoco pertenece el punto (5,4) pues 5%3=2; 5/3=1; 1%3=1 y por otro lado 4%3=1; 4/3=1; 1%3=1. Dado que en la primera iteración no se produjo la igualdad a 1 de los restos, seguimos con la segunda aplicando la división entera y hallando nuevamente los restos de los cocientes obtenidos.

En resumen, como los restos de la división entre 3 son un valor del conjunto {0, 1, 2}, lo que hacemos es comprobar si el punto es el valor central o centro de un cuadrado, en cuyo caso no pertenece al fractal. En la imagen los puntos en amarillo y azul no pertenecen al fractal. Los amarillos se encuentran con la primera iteración y los azules necesitan una segunda. Los puntos en negro son los que sí pertenecen y se dice que escapan de la selección del iterativo. En este caso necesitan siempre pasar todas las iteraciones hasta que los cocientes de las divisiones enteras sean cero, consumiento todo el bucle while.

Conjunto de Julia con el Trazador de Gráficas Matemáticas

El Conjunto de Julia es un fractal que se obtiene al aplicar la función compleja f_c(z)=z²+c, con la variable compleja z=(x,y) y la constante c=(a,b) que define el parámetro de la familia de funciones f_c. La imagen de la izquierda es la que corresponde a c=(-0.75,0), obtenida también con el Trazador de Gráficas Matemáticas. El código del JavaScript de este fractal se inicia con la definición de los rangos de iteración por el plano complejo i=-2..2|64; j=-2..2|64;. Recuerde que esto no es una expresión de JavaScript sino una definición de rangos de iteración particular para la aplicación trazadora. El rango [-2,2]×[-2,2] es el necesario para representar el conjunto de puntos de origen de un Julia. Con eso se definen dos bucles: el primero itera desde -2 hasta 2 en valores reales para la primera variable i. Por cada iteración de este hay otro bucle interior en el mismo rango para la variable j. En definitiva se trata de iterar por todos los puntos del plano. En este ejemplo el plano tiene un tamaño de 256×256 píxeles. Por lo tanto los dos bucles encadenados suponen 65536 iteraciones que en definitiva serán los puntos de ese plano. La declaración del rango la finalizamos con "|64" para realizar un mapeado 1:1, es decir, como la longitud del rango -2..2 es 4, entonces se muestrean 64×4=256 en cada eje desde el plano de origen, lo que da un total 256×256=65536 iteraciones que coincide también con el número de puntos del plano de destino. Más muestras de 64 no conducen a mejores resultados pues no hay más puntos de destino y sólo obtenemos más iteraciones. Menos muestras de 64 nos dará como resultado que no tendremos el rango [-2,2]×[-2,2] completo para todo el fractal.

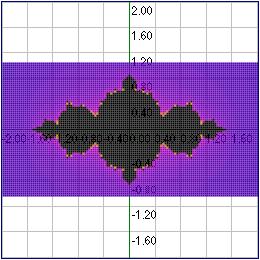En algún caso nos puede interesar mostrar sólo una porción en una dirección, por ejemplo, poniendo i=-2..2|64; j=-2..2|32; con lo que tendremos un muestreo de (4×64)×(4×32)=32768 puntos. La imagen de la izquierda es un ejemplo de la aplicación de esto, obtenida con precisión cero y contorno igual a 1 para observar las dimensiones [-2,2] en cada eje.

El código del algoritmo que selecciona los puntos es el siguiente:

i=-2..2|64; j=-2..2|64;
if (e==0){
   e=30; d=10; c=75; f=0.4;
   a=-3/4; b=0;
}
x=0; y=0; r=i; s=j;
for(k=0; k<e; k++){
   m=pow(r,2); n=pow(s,2);
   if ((m+n)>4) break;
   p=m-n+a; q=2*r*s+b;
   r=p; s=q;
}
if(k<e){
   if (c>1){
      if (k>(e*f)){u=50+c+k; v=0;}else{u=0; v=100+c+k;}
      color = "rgb("+(c+d*k)+","+u+","+v+")";
   } else {
      color = "white";
   }
} else {
   color="black";
}
x=i; y=j;
_anchoxy:256_altoxy:256_zoomx:80_zoomy:80_remarcar:0
_precision:1_ejes:0_subejes:0_graduacion:0_contorno:0
_usar-colores:1_movex:0_movey:0_trazar-lineas:0

Después de la declaración de rangos iniciamos las variables. En el Trazador de Gráficas las variables disponibles son todas las letras del conjunto ASCII a..z, iniciándose todas a cero. Por lo tanto en la primera iteración detectamos la variable e==0 e iniciamos las variables de nuestro algoritmo:

• Parámetro de Julia: a=-3/4; b=0; para el valor complejo c=(a,b) en la función f_c(z)=z²+c.
• Escape: e=30 que declara el máximo de iteraciones para la selección de puntos. Los puntos que pasan todo el bucle for son los que escapan al ∞ y se pintan de color negro. Son realmente los que forman el conjunto de Julia. El resto no escapan, pues en algún momento inferior al máximo se detectan y se rompe el bucle con break, pintándose de diferentes colores según los siguientes parámetros.
• Difuminado: d=10 y Color base c=75. El color de los puntos no escapados se aplica con alguna proporcionalidad sobre el momento en que dejan el bucle for (iteración k). Así la expresión c+d*k nos da un valor entero de color en la componente red de la función rgb(red,green,blue).
• Factor de pre-escape: f=0.4. Es un valor real del rango [0,1] que nos dará un límite menor que el máximo de escape (e*f) y con el que diferenciamos dos zonas por debajo y por arriba de ese valor.

En cada iteración ponemos x=0; y=0;, pues el Trazador pintará al final el punto (x,y). Luego analizamos sí el punto r=i; s=j; pertenece al fractal con el bucle for. La función sería f(r,s)=(r+i·s)²+a+i·b, que tiene las componentes Real e Imaginaria (p,q) siguientes:

• p = r² - s² + a
• q = 2·r·s + b

Para evitar hacer cálculos repetidos, elevamos al cuadrado m=r² y n=s². El punto no escapa si la suma de estos términos es mayor que 4. Realmente habría que analizar si el valor obtenido r+i·s es un punto que está dentro del círculo de radio 2 (recuerde que definimos este rango [-2,2]×[-2,2] en la exploración). Para eso habría que calcular (r²+s²)^1/2>2 pero esto equivale a (m+n)>4 evitando la raíz y calculando las potencias una única vez. Si esto no se cumple obtenemos el nuevo valor p,q y volvemos a iterar. Al final sí el punto inicial (i,j) pasó todo el bucle es que escapó al infinito y se pintará de color negro.

Conjunto de Mandelbrot con el Trazador de Gráficas Matemáticas

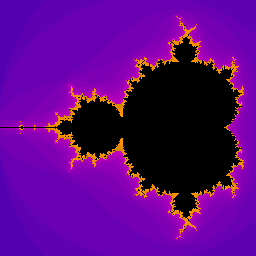
El Conjunto de Mandelbrot para f_c(z)=z²+c se obtiene ahora iterando por el plano de origen [-2,2]×[-2,2] y analizando cada pareja de valores del parámetro c=(a,b). El código es igual que el de Julia pero en el bucle de escape se analiza el parámetro, tal como aparece resaltado en amarillo en el código:

edita-funcion:i=-2..2|64; j=-2..2|64;
if(e==0){
    e=30; d=10; c=75; f=0.4;
}
x=0; y=0; r=0; s=0;
a=i; b=j;
for(k=0; k<e; k++){
   m=pow(r,2); n=pow(s,2);
   if ((m+n)>4) break;
   p=m-n+a; q=2*r*s+b;
   r=p; s=q;
}
if(k<e){
   if (c>1){
      if (k>(e*f)){u=50+c+k; v=0;}else{u=0; v=100+c+k;}
      color = "rgb("+(c+d*k)+","+u+","+v+")";
   } else {
      color = "white";
   }
} else {
   color="black";
}
x=i; y=j;
_anchoxy:256_altoxy:256_zoomx:100_zoomy:100_remarcar:0
_precision:1_ejes:0_subejes:0_graduacion:0_contorno:0
_usar-colores:1_movex:0.7_movey:0_trazar-lineas:0

Este es el código para la primera imagen del grupo de tres anteriores. Está centrada en el punto (x,y)=(-0.7,0), que se declara con movex:0.7_movey:0 indicando el movimiento en dirección contraria del plano relativo al centro de coordenadas (0,0). El valor de escape es e=30. El zoom tiene aquí valor 100 (declarado con zoomx:100_zoomy:100), de tal forma que el plano tiene unas dimensiones de 256×256 píxeles lo que supone una dimensión final de un plano 256/100=2.56, es decir 2.56×2.56 unidades. Este zoom relativo al plano 2×2=4 del muestreo del fractal es de 1.5625, pues 4/2.56=1.5625. En definitiva, la imagen está aumentada 1.5625 veces.

La segunda imagen está centrada en (-0.655,0.446). Tiene un escape e=1000. El zoom es de 11500 que lleva a un plano final de 256/11500=0.022260869 unidades de lado. El zoom relativo al plano de muestreo es de 4/0.022260869=179.6875.

La última imagen está centrada en (-0.29591,0.01734), con un escape de e=450. El zoom es de 60100 que nos da un plano final de 256/60100=4.2595×10^-3 unidades de lado. El zoom relativo al plano de muestreo es de 4/4.2595×10^-3=939.0625.