Fractales

Un fractal es una forma geométrica fragmentada que se repite a cualquier escala. Es un término propuesto por Benoît Mandelbrot considerado como el principal creador de la geometría fractal. Las imágenes que se generan resultan extrañamente atractivas. Pero no sólo son imágenes, pues parece que además la geometría fractal tiene aplicación en otras áreas de la ciencia y las matemáticas. También resulta atrayente para un programador el reto de generar fractales. Quiero iniciarme con algunos fractales básicos, como el triángulo y la alfombra de Sierpinski o el copo de nieve de Koch. Es necesario entender el concepto de recursividad en programación, que junto al uso del elemento canvas de HTML-5 me servirá para llevar a cabo esta primera inmersión en el mundo de los fractales.

Estos ejemplos contienen además una utilidad para ver paso a paso cómo se genera cada fractal. Todos los ejemplos han sido probados en los navegadores Chrome 16, Firefox 9, Opera 11.60, Safari 5.1 y Explorer 9. Explorer 8 no admite el elemento canvas. El código Javascript se encuentra dentro de la página junto a cada elemento por si quiere consultarlo.

El Triángulo de Sierpinski y el Sistema de Funciones Iteradas

El triángulo de Sierpinski puede generarse usando cuadrados y mediante un sistema de funciones iteradas. En síntesis se trata de dibujar un cuadrado relleno de color en un primer paso. En cada paso posterior se dibujan tres cuadrados de lado 1/2 del anterior. Uno de ellos si sitúa de tal forma que su vértice inferior derecho toque el vértice superior izquierdo del anterior. El otro se desplaza dos veces su lado a la derecha y el último se desplaza dos veces su lado hacia abajo. Esto lo puede ver con más claridad con la opción por pasos del script.

En cada iteración dibujamos 3 cuadrados por cada cuadrado dibujado en el paso anterior. Al mismo tiempo vamos reduciendo el tamaño de tal forma que cuando el lado sea de 1 píxel finalizaremos. El algoritmo es un recursivo:

function fractal(x,y,wa){
    var w = wa/2;
    if (w>=1){
        var x1 = x-w;
        var y1 = y-w;
        var x2 = x+w;
        var y2 = y-w;
        var x3 = x-w;
        var y3 = y+w;
        fractal(x1,y1,w);
        if (wa!=ww){
            fractal(x2,y2,w);
            fractal(x3,y3,w);
        }
    }
    dibujarForma(x1,y1,x2,y2,x3,y3,w);
}

Inicialmente llamamos al recursivo con fractal(ww,ww,ww). Empezamos en el punto (x,y) = (ww,ww), es decir, el vértice inferior derecho del contenedor canvas. El lado inicial será el ancho del elemento ww. Cada vez que entramos en el recursivo dividimos el lado por dos y ubicamos los tres nuevos cuadrados que se generan, a excepción de la primera entrada que sólo pintamos un único cuadrado. El límite del recursivo se establece cuando el lado sea igual a 1, que será el mínimo de resolución para dibujar en el Canvas.

El Triángulo de Sierpinski generado con triángulos

Otra alternativa para generar el Triángulo de Sierpinski usando triángulos.

Ahora el recursivo es el siguiente:

function fractalB(x,y,ba,ha){
    var b = ba/2;
    var h = ha/2;
    if ((b>=1)&&(h>=1)){
        var x2 = x+b/2;
        var y2 = y+h;
        var x3 = x-b/2;
        var y3 = y+h;
        fractalB(x,y,b,h);
        fractalB(x2,y2,b,h);
        fractalB(x3,y3,b,h);
    }
    dibujarFormaB(x,y+2*h,x2,y2,x3,y3);
}

LLamamos al recursivo con fractalB(wb/2,0,wb,hb) siendo wb,hb el ancho y alto del contenedor canvas. El punto inicial (x,y) es el vértice superior del triángulo exterior: el punto (wb/2, 0). Recuerde que en el canvas la coordenada Y positiva se dirige hacia abajo. El triángulo queda definido en la primera llamada con una base wb y una altura hb igual que las medidas ancho y alto del canvas. En cada iteración dibujamos un triángulo invertido en cada triángulo anterior. Por lo tanto se generan tres triángulos en cada iteración una vez que se divide la base y altura anterior por dos:

1. El superior con el vértice superior en el mismo punto (x, y)
2. El del lado derecho con el vértice superior en (x+b/2, y+h)
3. Y el del lado izquierdo con el vértice superior en (x-b/2, y+h)

Iteración aleatoria para genearar el Triángulo de Sierpinski

En los ejemplos anteriores se usa un Sistema de Funciones Iteradas que generan la forma definitiva. En el Triángulo de Sierpinski anterior necesitamos un conjunto de tres funciones que se aplican de forma recursiva. Pero también es posible usar un algoritmo de iteración aleatoria para generar el fractal.

Ahora no necesitamos ningún recursivo. Sólo tenemos que fijar el numero máximo de puntos que queremos pintar. La función fractalC(x,y,numPuntos) se llama inicialmente con numPuntos = 20000:

function fractalC(x, y, numPuntos){
    for (var i=0; i<numPuntos; i++){
        var vn = ((parseInt(Math.random()*1000))%3);
        x = x-((x-vert[vn][0])/2);
        y = y-((y-vert[vn][1])/2);
        cwxc.fillRect(x,y,1,1);
    }
}

El punto (x,y) pertenece al triángulo inicial y se elige antes de la llamada a esta función de forma aleatoria. Luego hacemos un bucle de 20.000 puntos eligiendo en cada pasada un vértice aleatorio. La función de Javascript Math.random() y el operador módulo nos dará un valor del conjunto {0,1,2} que usaremos como índice para extraer el punto (x,y) en el array vert=[[wc/2,0],[wc,hc],[0,hc]] (wc,hc son las dimensiones del contenedor canvas). Estos valores son los puntos de los tres vértices del triángulo inicial. Buscamos el nuevo punto en la mitad de la distancia entre el punto actual y el vértice aleatorio y pintamos ese nuevo punto. Tras un par de miles de puntos empezamos a ver como se va formando el fractal.

La Alfombra de Sierpinski

La Alfombra de Sierpinski es otro fractal similar a los anteriores.

Volvemos a usar un recursivo para aplicar las funciones iteradas. Ahora hemos de crear 8 copias del cuadrado y situarlas en torno al cuadrado de la iteración anterior. Inicialmente llamamos al recursivo con fractalD(wd,hd,wd,hd) siendo wd,hd el ancho y alto del contenedor canvas. Así el primer punto (x,y) es el vértice inferior derecho del contenedor. En cada pasada ese punto será el vértice superior izquierda de cada cuadrado que será dividido en tamaño por 3. Para automatizar la tarea de situar los 8 cuadrados usamos un array de desplazamientos desp=Array(-2, 1, 4). Partiendo de que el nuevo tamaño es w y la posición es el vértice superior izquierdo, los nuevos vértices estarán en el eje X una longitud de 2 veces ese tamaño a la iquierda (-2), 1 vez a la derecha (+1) y 4 veces a la derecha (+4). Lo mismo en el eje Y. Por lo tanto tenemos que hacer todas las combinaciones de esos desplazamientos. Obviamos el desplazamiento (1,1) pues corresponderá al que cae en el centro del anterior cuadrado que se desprecia.

function fractalD(x,y,w,h){
    var w = w/3;
    var h = h/3;
    if ((w>1)&&(h>1)){
        var desp = Array(-2, 1, 4);
        for (var i=0; i<desp.length; i++){
            var xd = x + desp[i] * w;
            for (var j=0; j<desp.length; j++){
                if (!((i==1)&&(j==1))){
                    var yd = y + desp[j] * h;
                    cwxd.fillRect(xd,yd,w,h);
                    fractalD(xd,yd,w,h);
                }
            }
        }
    }
}

El Copo de Nieve de Koch

El Copo de Nieve de Koch o Estrella de Koch también es un fractal que se genera con el sistema de funciones iteradas.

El algoritmo recursivo fractalRecta(xa,ya,xb,yb) se aplica a la recta que pasa por los puntos (xa,ya) y (xb,yb). Para controlar la terminación del recursivo medimos el largo de esta recta de tal forma que cuando sea de 1 píxel finalizamos la ejecución.

function fractalRecta(xa,ya,xb,yb){
    var largo = Math.sqrt(Math.pow(xb-xa,2) + Math.pow(yb-ya,2));
    if (largo > 1){
        //Dividimos la recta en 3 partes
        var sx = (xb-xa)/3;
        var sy = (yb-ya)/3;
        //Buscamos los puntos de las 4 rectas
        var x1 = xa;
        var y1 = ya;
        var x2 = xa + sx;
        var y2 = ya + sy;
        var vx = (Math.sqrt(3)/6)*(xb-xa);
        var vy = (Math.sqrt(3)/6)*(yb-ya);
        var x3 = x1 + ((xb-xa)/2) - vy;
        var y3 = y1 + ((yb-ya)/2) + vx;
        var x4 = xb - sx;
        var y4 = yb - sy; 
        var x5 = xb;
        var y5 = yb;
        //Borramos recta anterior
        cwxe.beginPath();
        cwxe.moveTo(xa,-ya+he);
        cwxe.lineTo(xb,-yb+he);
        cwxe.stroke();
        cwxe.closePath();
        //Pintamos las 4 nuevas rectas
        cwxe.beginPath();
        cwxe.moveTo(x1,-y1+he);
        cwxe.lineTo(x2,-y2+he);
        cwxe.lineTo(x3,-y3+he);
        cwxe.lineTo(x4,-y4+he);
        cwxe.lineTo(x5,-y5+he);
        cwxe.fill();
        cwxe.closePath();
        //Nueva llamada recursiva a cada segmento
        fractalRecta(x1,y1,x2,y2);
        fractalRecta(x2,y2,x3,y3);
        fractalRecta(x3,y3,x4,y4);
        fractalRecta(x4,y4,x5,y5);
    }
}

Esa recta que pasa por (xa,ya) y (xb,yb) se divide en 3 segmentos de igual longitud donde el central genera a su vez 2 más al formar el triángulo equilatero. Los nuevos puntos que delimitan las 4 rectas nuevas son:

• (x1,y1) = (xa, ya)
• (x2,y2) = (xa + sx, ya + sy)
• (x4,y4) = (xa - sx, ya - sy)
• (x5,y5) = (xb, yb)
• (x3,y3). Este es el que lleva más trabajo buscar pues hay que aplicar algo de geometría. A mí se me ocurre hacerlo así:
  
  Consideramos el segmento entre los puntos (x_a , y_a) hasta (x_b , y_b)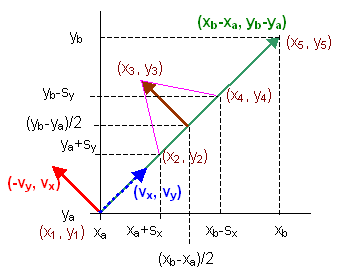
  Las componentes XY de un tercio de ese segmento serán:
  s_x =  (x_b − x_a) / 3
  s_y =  (y_b − y_a) / 3.
  Con esto ya determinamos los puntos (x₁ , y₁), (x₂ , y₂), (x₄ , y₄), (x₅ , y₅) de forma sencilla tal como señalamos antes. Para hallar el punto (x₃ , y₃) tomamos el segmento inicial como un vector (en color verde). Sea ese vector R(x_b−x_a , y_b−y_a) siendo d=|R| su módulo, es decir la longitud de la recta inicial. Un vector unitario en esa misma dirección será:
  U((x_b−x_a)/d , (y_b−y_a)/d)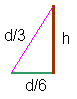

  Por otro lado apreciamos que el triángulo central ha de ser equilatero y viendo que cada segmento de los 4 que se generan tiene una longitud de d/3, entonces buscamos la altura de ese triángulo equilatero:
  h = ((d/3)²+(d/6)²)^1/2 = 3^1/2d/6
  Bueno, esto es evidente, pues la altura de un triángulo equilatero de lado a es 3^1/2a/2 y en nuestro caso el lado vale d/3.

  El vector V(v_x , v_y) (en color azul) tendrá un módulo h y la dirección del vector unitario U:
  V(v_x , v_y) = h·U = 3^1/2(d/6)·((x_b−x_a)/d , (y_b−y_a)/d) = (3^1/2/6)·(x_b−x_a , y_b−y_a)
  Este vector en color azul V(v_x , v_y) tiene el mismo tamaño que el vector en color marrón que nos servirá para buscar el punto (x₃ , y₃). Entonces uno ortogonal a V será (−v_y , v_x) obteniéndose el vector de color rojo, con lo que sólo nos faltará trasladarlo hasta el punto apropiado para obtener el de color marrón. Entonces las coordenadas del punto buscado son:
  x₃ = x₁ + ((x_b−x_a)/2) − v_y
  y₃ = y₁ + ((y_b−y_a)/2) + v_x
  

Finalmente tendremos 4 nuevas rectas delimitadas por los puntos x1, y1, x2, y2, x3, y3, x4, y4, x5, y5 a las que aplicaremos recursivamente la misma función fractalRecta(). Pero antes de esta llamada borramos la recta anterior y luego pintamos los nuevos 4 segmentos. En este script todos los cálculos se hacen en el eje de coordenadas Y normal, es decir, el contrario al que usa canvas. Por eso en el momento de pintar los segmentos trasladamos la coordenada vertical poniendo -yi+he pues he es la altura del canvas.

Lo anterior construye el fractal para una recta. Para aplicarlo inicialmente lo ejecutamos sobre 3 rectas que forman un triángulo inicial. El script de la primera llamada es el siguienet, donde we,he son las medidas del contenedor canvas.

//Calculamos los puntos de un triángulo inicial
var p1x = we/2-lado/2;
var p1y = he/2-altura/3;
var p2x = p1x+lado;
var p2y = p1y;
var p3x = p1x+lado/2;
var p3y = p1y+altura;
//Lo pintamos
cwxe.beginPath();
cwxe.moveTo(p1x,-p1y+he);
cwxe.lineTo(p2x,-p2y+he);
cwxe.lineTo(p3x,-p3y+he);
cwxe.lineTo(p1x,-p1y+he);
cwxe.fill();
cwxe.closePath();
//Llamamos al fractal por primera vez
fractalRecta(p1x,p1y,p3x,p3y);
fractalRecta(p3x,p3y,p2x,p2y);
fractalRecta(p2x,p2y,p1x,p1y);

Se trata de pintar un triángulo equilatero inicial de lado=we*2/3 y altura=lado*Math.sqrt(3)/2, centrándolo en el canvas. Luego llamamos a los 3 fractales de las rectas de los lados de ese triángulo.