El redondeo estándar en JavaScript ES6
Redondear números fraccionarios con la regla del redondeo estándar
El redondeo estándar de fracciones 0.5 se basa que entre 0 y 4 hay cinco números que redondean hacia abajo, mientras que entre 5 y 9 hay otros cinco que redondean arriba. Así las fracciones 0.5 siempre redondean arriba. Se trata de observar el siguiente dígito después de los especificados para redondeo y si es igual o mayor que 5 redondeará arriba, en otro caso se quedará como está.
Por ejemplo, redondear 1.025 a dos dígitos resultará 1.03. Esta regla es la que se utiliza en aplicaciones contables y de gestión comercial. Como cuando implementamos una plantilla para calcular una factura, tal como veremos en el último apartado de este tema.
Sin embargo no debemos olvidar lo que comentamos en el tema anterior, pues si fracciones 0.5 siempre redondean arriba, en algunos casos de operaciones acumuladas podrían producirse desviaciones.
Hemos de implementar una función que redondee las fracciones 0.5 siempre arriba. Si no podemos evitar la desviación comentada en el párrafo anterior, sí que podemos hacer que al menos sea una regla equilibrada en positivos y negativos. Así por ejemplo 1.025 debe redondear a 1.03 y -1.025 a -1.03. La regla lejos de cero sería equivalente a una estándar pero para redondeo al entero más cercano y es equilibrada en este aspecto:
function redondearLejosDeCero(numero){
return Math.sign(numero) * Math.floor(Math.abs(numero) + 0.5);
}
console.log(redondearLejosDeCero(102.5)); // 103
console.log(redondearLejosDeCero(-102.5)); // -103
Como explicaremos en el siguiente apartado, los métodos toFixed(), toExponential() ni toPrecision() tampoco sirven para el redondeo estándar:
// 1.025 no redondea a 1.03
let n = 1.025;
console.log(n.toFixed(2)); // 1.02
console.log(n.toExponential(2)); // 1.02e+0
console.log(n.toPrecision(3)); // 1.02
El método toLocaleString() si implementa ese redondeo cuando usamos un formato de moneda. El resultado se obtiene en un string con ese formato, siendo incómodo usar ese valor para cálculos numéricos posteriores:
// 1.025 sí redondea a 1.03
let n = 1.025;
console.log(n.toLocaleString("es",
{style: "currency", currency: "EUR"})); // 1,03 €
Por lo tanto intentaremos construirnos una función para el redondeo estándar, función que nos devolverá un tipo number. Retomamos el primer apartado del tema anterior donde exponíamos que podemos redondear un número real a un determinado número de dígitos decimales con estas operaciones:
Esto lo podemos implementar con el método Math.round(numero) que redondea al entero más cercano:
function redondear(numero, digitos){
let base = Math.pow(10, digitos);
let entero = Math.round(numero * base);
return entero / base;
}
Con esta función que nos hemos construido podemos redondear números, de tal forma que una fracción igual o mayor que 0.5 redondea hacia arriba:
console.log(redondear(1.114, 2)); // 1.11
console.log(redondear(1.115, 2)); // 1.12
console.log(redondear(1.116, 2)); // 1.12
Pero eso no siempre es cierto para todos los números. Por ejemplo 1.025 redondea a 1.02, hacia abajo, mientras que 1.045 si redondea hacia arriba resultando 1.05:
console.log(redondear(1.025, 2)); // 1.02
console.log(redondear(1.045, 2)); // 1.05
Veamos paso a paso lo que está pasando con el redondeo del número 1.025:
let numero = 1.025, digitos = 2;
let base = Math.pow(10, digitos);
console.log(base); // 100
let producto = numero * base;
console.log(producto); // 102.49999999999999
let entero = Math.round(producto);
console.log(entero); // 102
console.log(entero / base); // 1.02
Observamos que el producto numero × base contiene una aproximación debida al redondeo del formato IEEE754. Lo comprobamos realizando la multiplicación binaria de 1.025 × 100
La parte resaltada son los bits que exceden el formato. Como el primero es un cero redondea al inferior, quedando la parte en azul tal como está. Su valor decimal es:
La función redondear() no redondea bien con el número 1.025 como hemo visto. Pero sin embargo con 2.025 no se produce ese efecto. Probemos con ese 2.025 que debe redondear a 2.03. El formato IEEE754 es:
Se observa como 2.025 tiene un exponente uno, que quitamos corriendo
la coma para llevar a cabo la multiplicación 2.025 × 100:
El redondeo del formato será hacia arriba dado que el primer bit de los que exceden en rojo es uno. Así que nos quedará el número
siendo un binario exacto con valor 202.5, con lo que Math.round(202.5) nos devolverá 203. Finalmente al dividir entre 100 obtendremos el esperado 2.03.
Pero aunque 2.025 redondee bien a 2.03 tenemos el problema de que -2.025 redondea -2.02 en lugar de -2.03. Por tanto la función redondear() no es equilibrada en positivos y negativos dado que Math.round() tampoco lo es, ya que usa la regla más infinito que vimos en el tema anterior:
//Regla no equilibrada positivos y negativos
console.log(redondear(2.025, 2)); // 2.03
console.log(redondear(-2.025, 2)); // -2.02
//pues Math.round() no es equilibrada
console.log(Math.round(202.5)); // 203
console.log(Math.round(-202.5)); // -202
Podríamos usar la regla lejos de cero en lugar de Math.round(). Redondearía de forma equilibrada ±2.025 a ±2.03, pero seguiría sin redondear adecuadamente valores ±1.025 resultando como antes ±1.02, motivado por el redondeo del formato IEEE754:
function redondearLejosDeCero(numero){
return Math.sign(numero) * Math.floor(Math.abs(numero) + 0.5);
}
function redondear(numero, digitos){
let base = Math.pow(10, digitos);
let entero = redondearLejosDeCero(numero * base);
return entero / base;
}
//Redondeo correcto equilibrado para este valor
console.log(redondear(2.025, 2)); // 2.03
console.log(redondear(-2.025, 2)); // -2.03
//Pero el problema con el formato IEEE754 sigue existiendo
console.log(redondear(1.025, 2)); // 1.02
console.log(redondear(-1.025, 2)); // -1.02
Así que para el resto de este tema dejaremos la función redondear() basada en Math.round(), porque en el fondo vamos a prescindir de ella y crear otra función redondearExp() que arregla el problema del redondeo del formato IEEE754. En un ejemplo interactivo que veremos más abajo sobre diferencias de redondeos entre toFixed(), redondear() y redondearExp(), se puede comprobar que entre 1 y 100 tomando números con tres dígitos fraccionarios aparecen 568 diferencias como resultado de que toFixed() se comporta como redondear() y a su vez distinto de redondearExp(). Son números con fracción 0.5 como 1.005, 1.015, 1.025, ..., 2.155, ..., 34.785, ..., 81.865.
Esos números son tales que al multiplicarlos por 100 originan un exceso de fracción cuyo primer bit es un cero, lo que hace que el formato IEEE754 lo redondee hacia abajo. Por ejemplo, con 34.785:
Multipliquemos por 100:
Se observa que el primer bit de exceso en rojo es un cero, por lo que el número aproxima hacia abajo, es decir, la parte en azul se queda como está. Esto ocasiona que 34.785 × 100 = 3478.499999999999, aplicando Math.round() redondeará a 3478 y dividiendo entre 100 obtendremos 34.78 en lugar de 34.79 que sería el esperado.
Redondeando con el método toFixed()
Podíamos pensar en usar el método num.toFixed(), pero parece que el problema se complica. Cuando con el anterior método redondear() el número 1.045 resultaba en 1.05 mientras que 1.025 se quedaba en 1.02, ahora con toFixed() ambos números redondean hacia abajo:
// El método toFixed() redondea abajo algunas fracciones 0.5
console.log((1.025).toFixed(2)); // 1.02
console.log((1.045).toFixed(2)); // 1.04
//Mientras que nuestra función redondea abajo y arriba
console.log(redondear(1.025, 2)); // 1.02
console.log(redondear(1.045, 2)); // 1.05
Pero esto no pasa con todos los números con fracción 0.5, algunos redondean hacia arriba, coincidiendo también con la función redondear() que vimos en el apartado anterior:
//En este caso ambos redondean arriba las fracciones 0.5
console.log((1.125).toFixed(2)); // 1.13
console.log((1.145).toFixed(2)); // 1.15
console.log(redondear(1.125, 2)); // 1.13
console.log(redondear(1.145, 2)); // 1.15
¿Qué es lo que está pasando aqui? Vayamos a la especificación EcmaScript 2016 para ver que nos dice acerca del método toFixed(). Dice que si aplicamos el método a un número x con una fracción de dígitos f, JavaScript debe encontrar un entero n que haga que el valor matemático de n / 10f - x esté tan cercano a cero como sea posible. Si se dieran dos valores de n con igual distancia, cogeríamos el más grande.
Para obtener el número real redondeado tomaríamos el entero n y le ubicaríamos una coma decimal para que tuvieran tantos dígitos fraccionarios como los especificados en la fracción de dígitos f.
Lo que no dice la especificación es como obtener ese entero n. Ignoremos esto, pues lo que nos interesa es entender la razón del redondeo del método y no necesariamente saber cómo el navegador lo implementa. Hagamos el ejemplo con (1.025).toFixed(2) y ver por qué redondea a 1.02 en lugar de 1.03. Tenemos estas variables:
Los números enteros elegidos son 102 y 103, pues al ubicar la coma los 2 lugares que nos dice la variable f los posibles redondeos serían 1.02 o 1.03. Calculamos las distancias:
Existe la misma distancia entre ambos, por lo que el elegido debería ser el 103 así que el redondeo sería 1.03. Pero el método toFixed() nos devuelve 1.02. Sin embargo hemos cometido un error realizando las operaciones en base decimal, pues tendríamos que haberlas hecho en binario, pues así se realizan todos los cálculos en un ordenador. Vamos a hacerlo.
Buscamos en el formato IEEE754 los tres números 102, 103 y 1.025 con el convertidor IEEE754:
Quitamos exponentes y hacemos la primera división 102/100:
Observamos que el primer dígito resaltado es un uno y el resto no son ceros, por lo que la regla de redondeo del formato redondeará hacia arriba ese número pasando de ···10001 a ···10010. Tomamos ese número ya redondeado y le restamos 1.025:
Ese número, que es la distancia 102/100-1.025, no tiene bits sobrantes a la derecha, por lo que no hay nada que redondear. Vamos a dividir ahora 103/100:
Nuevamente hay que hacer un redondeo hacia arriba. Lo hacemos y le restamos 1.025:
Tampoco sobran bits por lo que no hay que redondear. Ese número es la distancia 103/100-1.025. La primera distancia es negativa, está por debajo de 1.025. La segunda es positiva, está por encima. ¿Cuál es la menor de las dos en valor absoluto? Comparamos el valor absoluto de ambas distancias para ver cuál es más pequeño:
Es evidente que la primera es un bit más pequeña, con lo que el entero elegido será 102 así que 1.025 será redondeado a 1.02.
Hacemos las mismas operaciones para resolver (1.125).toFixed(2) que redondea a 1.13, siendo los enteros a probar 112 y 113. En primer lugar la división 112/100, que origina un redondeo arriba del formato:
La primera distancia es entonces:
Ahora vemos la división 113/100 que origina redondeo hacia abajo:
Esta es la segunda distancia:
Se observa claramente que D1 = D2, estando a la misma distancia, por lo que tomaremos el entero más grande 113, como dice la especificación, así que 1.125 redondeará a 1.13.
El redondeo estándar en JavaScript
Hemos visto que no conseguimos redondeo estándar con toFixed() ni con la función redondear() para números como 1.025. Pero la idea inicial para redondear expuesta en el primer apartado sigue siendo correcta. El problema con la función redondear() está cuando obtenemos la base como producto numero × 10digitos. En el siguiente código se puede comprobar que para redondear el número 1.025 con 2 dígitos necesitamos hacer el producto 1.025 × 100. Debería dar 102.5 pero como ya vimos en un apartado anterior, resulta 102.49999999999999 debido a la operación de multiplicación y al redondeo del formato IEEE754. Aplicar Math.round() a ese valor devuelve 102 en lugar del esperado 103:
let numero = 1.025, digitos = 2;
let base = numero * Math.pow(10, 2);
console.log(base); // 102.49999999999999
console.log(Math.round(base)); // 102
La solución pasa por evitar esa operación de multiplicación intermedia. Y hay una forma si usamos el formato exponencial, pues el producto 1.025 × 100 podríamos expresarlo como 1.025×102. Así no realizamos ninguna multiplicación que es la causa del origen del redondeo del formato IEEE754. Luego vemos que Math.round() de ese formato exponencial redondea a 103 como se espera:
console.log(Math.round(1.025 * 100)); // 102
console.log(Math.round(1.025e2)); // 103
Tenemos que implementar un función para hacer la multiplicación en la forma 1.025e2. A continuación redondeamos ese número y luego dividimos también usando el formato exponencial 103e-2, resultando el número 1.03 esperado. Una primera aproximación a esa implementación podría ser la siguiente:
let numero = 1.025, digitos = 2;
let entero = Math.round(Number(numero + "e+" + digitos));
let redondeado = Number(entero + "e-" + digitos);
console.log(redondeado); // 1.03
Pero el número inicial puede venir en formato exponencial. O bien al obtener el entero podría venir representado en ese formato. Vea el apartado toString() para ver más detalles sobre eso. Tenemos que detectar esos formatos exponenciales:
let numero = 1.025e-10, digitos = 12;
//Multiplicamos y redondeo entero
let arr = numero.toString().split("e");
let mantisa = arr[0], exponente = digitos;
if (arr[1]) exponente = Number(arr[1]) + digitos;
let num = Number(mantisa + "e" + exponente.toString());
let entero = Math.round(num);
//Dividimos
arr = entero.toString().split("e");
mantisa = arr[0], exponente = -digitos;
if (arr[1]) exponente = Number(arr[1]) - digitos;
num = Number(mantisa + "e" + exponente.toString());
//Resultado redondeado
console.log(num); // 1.03e-10
En el código anterior hemos usado otro número de prueba que se representa con el formato exponencial 1.025×10-10 al aplicarle toString(). Lo redondeamos a 12 dígitos resultando el correcto redondeo 1.03×10-10.
Observamos una parte del código que se repite, por lo que podemos reducirlo a una función toExp() que nos devuelve siempre un formato exponencial, sumando con el signo los dígitos al exponente que ya pudiera tener:
function toExp(numero, digitos){
let arr = numero.toString().split("e");
let mantisa = arr[0], exponente = digitos;
if (arr[1]) exponente = Number(arr[1]) + digitos;
return Number(mantisa + "e" + exponente.toString());
}
let numero = 1.025e-10, digitos = 12;
//Multiplicamos y redondeo entero
let entero = Math.round(toExp(numero, digitos));
//Dividimos
let num = toExp(entero, -digitos);
console.log(num); // 1.03e-10
El código anterior aún podría mejorarse en un aspecto. Y es que no es equilibrado en positivos y negativos. Al final se basa en Math.round(). Tal como vimos aplica la regla que redondea arriba hacia +∞, con lo que 102.5 redondea a 103 pero -102.5 redondea a -102:
console.log(Math.round(102.5)); // 103
console.log(Math.round(-102.5)); // -102
Con el código de la función tal como está, redondear -1.025 a dos dígitos resultaría -1.02. Para evitar eso planteamos esta solución, que a la vez resultará en la función redondearExp() para redondear usando la multiplicación y división exponencial:
function redondearExp(numero, digitos) {
function toExp(numero, digitos){
let arr = numero.toString().split("e");
let mantisa = arr[0], exponente = digitos;
if (arr[1]) exponente = Number(arr[1]) + digitos;
return Number(mantisa + "e" + exponente.toString());
}
let entero = Math.round(toExp(Math.abs(numero), digitos));
return Math.sign(numero) * toExp(entero, -digitos);
}
Se observa que usamos el valor absoluto del número obtenido con Math.abs() y devolvemos el resultado con el signo obtenido con Math.sign(). Así los valores se redondean siempre como positivos hacia +∞, pero si el número es negativo es como si lo redondeáramos hacia -∞, lo que puede traducirse como un redondeo lejos de cero que logra el equilibrio deseado.
En este ejemplo puede probar los tres tipos de redondeos vistos: toFixed(), redondear() y redondearExp():
Ejemplo: Métodos de redondeo decimal
| Método | Valor |
|---|---|
toFixed() | |
redondear() | |
redondearExp() |
En este ejemplo realizamos un muestreo de números y presentamos los que difieren entre los tres métodos toFixed(), redondear() y redondearExp(), función que suponemos que realiza el correcto redondeo estándar. Con la primera opción buscamos que al menos uno de los tres sea distinto. Por ejemplo, si ponemos el entero de partida 1 y buscamos diferencia con redondeo a 2 dígitos, recorreremos los números con un dígito fraccionario más: 1.001, 1.002, 1003, ..., 1.998, 1.999, presentando sólo aquellos casos donde los tres métodos no resulten con el mismo valor. Aunque se recorren todos los números, veremos que las diferencias aparecen con algunas fracciones 0.5 exactas.
Con la segunda opción buscamos diferencias tales que toFixed() se comporta como redondear() y a su vez distintos de redondearExp(). Esto pone en evidencia los números como 1.025 que redondea a 1.02 con las dos primeras funciones y a 1.03 correctamente con redondearExp().
Ejemplo: Diferencias en redondeos con fracción 0.5
| Número | toFixed() | redondear() | redondearExp() |
|---|---|---|---|
Redondeando operaciones aritméticas
En el apartado anterior vimos que redondearExp() soluciona los problemas que nos daba toFixed() y redondear() con fracciones 0.5. Pero aún así la ejecución de operaciones con el formato IEEE754 nos seguirá dando otra clase de problemas.
Sabemos que la operación aritmética a+a×b debe darnos el mismo resultado que a×(1+b), dado que se aplica la propiedad distributiva de la multiplicación sobre la suma. Por ejemplo, siendo a = 171 y b = 0.015 es obvio que ambas operaciones dan lo mismo si lo hacemos con una calculadora con más precisión que la de JavaScript:
Si aplicara un método que redondee arriba la fracción 0.5 como redondearExp(), ambos valores nos darían 173.57 que sería el valor esperado. Pero en JavaScript y en general con el formato IEEE754 de 64 bits las cosas no funcionan así. La primera operación da el resultado esperado, pero la segunda no:
//La propiedad distributiva de la multiplicación sobre la suma
//garantiza que a*(b+c) = a*b+a*c, con lo que si a=171, b=1,
//c=0.015 entonces 171*(1+0.015) = 171*1 + 171*0.015
//¿Pero no es así con los números en JavaScript?
console.log(171 + 171 * 0.015); // 173.565
console.log(171 * (1 + 0.015)); // 173.56499999999997
Aunque suponga un esfuerzo de cálculo, vamos a realizar ambas operaciones binarias para entender por qué la primera resulta el valor exacto 173.565 y la segunda 173.56499999999997. Los dos números que intervienen en la primera operación son los siguientes:
Hágamos la multiplicación binaria de 171 × 0.015 como hemos realizado en apartados anteriores:
Los bits en rojo del resultado exceden el formato IEEE754 por lo que procede el redondeo arriba, sumando un bit a la parte en azul. Ahora sumamos el binario de 171 al resultado anterior:
El primer bit excedente es un cero, por lo que el formato redondea abajo dejando la parte en azul tal como está. Calculamos el valor decimal con una calculadora que tenga más precisión que los 64 bits del formato IEEE754 de JavaScript.
Se observa que el número se redondea a 173.565 siendo el resultado esperado de la operación 171 + 171 × 0.015.
Veámos ahora la segunda operación 171 × (1 + 0.015). Realmente tenemos que considerar 171 × 1.015, pues la suma binaria 1 + 0.015 no introduce desviación alguna. Estos son los formatos IEEE754 de los números que intervienen:
La multiplicación binaria de 171 × 1.015 será la siguiente:
Se observa que el primer dígito en rojo que excede el formato es un cero, por lo que procederá redondear abajo quedando la parte izquierda en azul tal como está. Calculemos el valor decimal del resultado:
Se observa en rojo los dígitos decimales que exceden de 17, realizándose otro redondeo arriba quedando el mismo número 173.56499999999997 que más arriba nos calculó JavaScript. Por lo tanto hay una desviación con el resultado esperado que debería ser 173.565.
Si tras cada resultado lo redondeamos con los tres métodos que conocemos observamos que incluso con redondearExp() no obtenemos el mismo valor para ambas operaciones:
let n1 = 171 + 171 * 0.015;
let n2 = 171 * (1 + 0.015);
//Con toFixed() ambos resultados son iguales, pero incorrectos
console.log(n1.toFixed(2), n2.toFixed(2)); // 173.56 173.56
//Con redondear() el primero es correcto pero no el segundo
console.log(redondear(n1, 2), redondear(n2, 2)); // 173.57 173.56
//Igual que le pasa a redondearExp()
console.log(redondearExp(n1, 2), redondearExp(n2, 2));// 173.57 173.56
Este problema se puede manifestar en la vida real con mayor frecuencia de la que pensamos. Supongamos que tenemos un importe y una tasa de recargo. ¿Cómo obtenemos el recargo redondeado a dos dígitos fraccionarios? ¿Usando importe+importe×tasa? ¿O con importe×(1+tasa)?
En este ejemplo puede probar importes y tasas para ver donde se manifiestan las diferencias entre ambas operaciones:
Ejemplo:
tal que
sea distinto de
con los métodos de redondeo f1 = z.toFixed(2), f2 = redondear(z, 2) y f3 = redondearExp(z, 2).
| importe | tasa | importe+importe×tasa | importe×(1+tasa) | ||||
|---|---|---|---|---|---|---|---|
| f1 | f2 | f3 | f1 | f2 | f3 | ||
¿Cómo resolvemos esto? Hemos estado viendo que los números se ajustan a una representación del formato IEEE754. Y esto puede ser un bit arriba o abajo menos significativo de la mantisa del formato. Por efecto del exponente, realmente la separación entre dos números del formato es exactamente de un espaciado. Su valor es 2nε, siendo n = Floor(log2 k) para un número dado k.
La idea para resolver el problema de la pérdida de precisión en las operaciones se basa en sumar un espaciado al resultado de la operación. Nos apoyaremos en la certeza de que ese espaciado es muy pequeño en comparación a los dígitos sobre los que luego vamos redondear. Así cuando la representación este por debajo del valor esperado por motivo del redondeo abajo del formato IEEE754, la suma del espaciado lo resituará en su valor. Si el resultado fuese exacto o estuviese por encima porque el redondeo del formato fue hacia arriba, la suma del espaciado seguirá siendo no significativa pues luego vamos a redondear a muchos menos dígitos. Veamos esto en ejecución:
let numero = 171 * (1 + 0.015);
//La operación hizo que el formato IEEE754 redondeara un bit abajo
console.log(numero); // 173.56499999999997
//El número esperado es 173.565, hay un espacio entre ambos de:
console.log(173.565 - numero); // 2.842170943040401e-14
//Vamos a calcular el espaciado del número
let n = Math.floor(Math.log2(numero));
console.log(n); // 7
let espaciado = Math.pow(2, n) * Number.EPSILON;
//El espaciado es el mismo que el calculado antes
console.log(espaciado); // 2.842170943040401e-14
//Lo sumamos para que alcance 173.565
numero += espaciado;
console.log(numero); // 173.565
//Ahora el redondeo es el esperado
console.log(redondearExp(numero, 2)); // 173.57
Para no tener que estar calculando el espaciado cada vez que hagamos una operación, ponemos un tercer argumento en la función redondearExp(numero, digitos, masEspaciado=false), de tal forma que cuando queramos redondear un número procedente de una operación forzaremos el tercer argumento a verdadero agregándose un espaciado al número antes de redondear al número de dígitos del segundo argumento. Observe como las dos operaciones dan ahora lo mismo:
console.log(redondearExp(171+171*0.015, 2, true)); // 173.57
console.log(redondearExp(171*(1+0.015), 2, true)); // 173.57
Se observa que el redondeo a dos dígitos supone una centésima arriba o abajo, es decir, una diferencia en valor absoluto de 10-2. Mientras que el espaciado para el número del ejemplo anterior era aproximadamente 2.84×10-14. Mientras este valor sea significativamene menor que 10-2 la suma del espaciado no afectará al redondeo.
De hecho es suficiente con que el espaciado sea menor que 10-digitos-1. Por ejemplo, para dos digitos habrá de ser menor que 10-3, pues es en el tercer dígito donde se actúa sobre el redondeo cuando es menor o mayor o igual que cinco. Si tenemos el número 173.56499999999997 para redondear a dos dígitos, señalando en rojo el tercer dígito donde actúa el redondeo, cualquier número menor que 0.001 puede ser sumado al anterior que, en todo caso y por acarreo del cuarto, incrementará en una unidad ese tercer dígito. Es decir, podemos sumar 173.56499999999997 + 0.0009 resultando 173.56589999999997 y sin modificar el segundo dígito.
Hemos agregado estas mejoras a la función redondearExp() quedando con el código final siguiente:
function redondearExp(numero, digitos, masEspaciado=false) {
function toExp(numero, digitos){
let arr = numero.toString().split("e");
let mantisa = arr[0], exponente = digitos;
if (arr[1]) exponente = Number(arr[1]) + digitos;
return Number(mantisa + "e" + exponente.toString());
}
let absNumero = Math.abs(numero);
let signo = Math.sign(numero);
if (masEspaciado){
let n = Math.floor(Math.log2(absNumero));
let spacing = Math.pow(2, n) * Number.EPSILON;
if (spacing < Math.pow(10, -digitos-1)) {
absNumero += spacing;
}
}
let entero = Math.round(toExp(absNumero, digitos));
return signo * toExp(entero, -digitos);
}
Pudiera darse el caso que con números cuya parte entera sea grande pudiera tener un espaciado amplio que pudiera entrar en conflicto con los dígitos a redondear. Por ejemplo, los números en el rango [8589934592, 17179869184) tienen un espaciado de aproximadamente 1.9×10-6. Como 1.9×10-6 < 10-5 entonces sólo podremos redondear hasta 4 dígitos con ese número. El código anterior detectaría el caso y omitiría sumar el espaciado, pues de otra forma podríamos modificar incorrectamente el dígito siguiente al de redondeo.
De todas formas con el formato IEEE754 sólo podemos asegurar hasta 16 dígitos significativos. El mayor del rango anterior tiene 11 dígitos enteros. Podríamos agregar entonces hasta 5 dígitos fraccionarios, por lo que es obvio que no podemos redondear más de 4 con el ajuste de sumar el espaciado, pues el quinto es el siguiente que necesitaremos para resolver el redondeo. En el siguiente código probamos con un número perteneciente al rango [8589934592, 17179869184) mencionado antes:
//Con 17 dígitos significativos...
let numero = 12345678901.234567;
//...el formato IEEE754 nos convierte el último 7 en 8
console.log(numero); // 12345678901.234568
//Por lo tanto sólo es seguro hasta 16 dígitos significativos
numero = 12345678901.23456;
console.log(numero); // 12345678901.23456
//Calculemos espaciado para ese número
let n = Math.floor(Math.log2(numero));
let espaciado = Math.pow(2, n) * Number.EPSILON;
console.log(espaciado); // 0.0000019073486328125
//¿Sumamos espaciado antes del redondeo con 5 dígitos?
console.log(espaciado < Math.pow(10, -5-1)); // false
//¿Y con 4 dígitos?
console.log(espaciado < Math.pow(10, -4-1)); // true
Las limitaciones del formato IEEE754 de 64 bits
Lo visto en el apartado anterior es una de las limitaciones del formato IEEE754 de 64 bits. Poco podemos hacer cuando los números sólo nos permiten 16 dígitos significativos. Si usamos 11 para la parte entera, sólo nos quedarán 5 para la fraccionaria. En estas condiciones no tiene sentido redondear a más de 4 dígitos.
Si el formato fuera mayor de 64 bits podríamos evitar muchos problemas. Por ejemplo, agregando 4 bits a la mantisa del formato obtendríamos el resultado 171 × 0.015 = 173.565 en lugar del que se obtiene 173.56499999999997. En el siguiente cálculo obtenemos la representación binaria de 1.015 con 57 bits en la mantisa, agregando 4 bits más a los 53 del formato IEEE754. Esos bits de más aparecen con color magenta. Con ese formato hacemos la multiplicación binaria 171 × 0.015:
Los bits que exceden del nuevo formato redondearían abajo pues el primer bit que excede es un cero. Calculemos el valor decimal ahora, teniendo en cuenta que al usar el convertidor binario-decimal no podemos pasarnos del máximo entero seguro. Para ello separamos el binario en dos partes, calculando como siempre el último paso con una calculadora de mayor precisión que la que ofrece JavaScript:
Observe como los cuatro bits hacen que el último dígito fraccionario de 17 bits significativos termine en 9 y el primero del excedente empiece en 7, lo que redondea a 173.565. Compare ese número obtenido con 57 bits en la mantisa con el que obtuvimos más arriba usando el formato IEEE754 de 53 bits en la mantisa:
Si en lugar de un formato IEEE754 de 64 bits tuviésemos uno de 128 bits nos olvidaríamos de algunos problemas expuestos en este tema. También habría pérdida de precisión en los cálculos pues eso es inevitable sea cual sea el tamaño del formato. Pero se manifestarían cuando se usaran más dígitos fraccionarios en los operandos que los sólo tres del número 1.015 que interviene en las operaciones anteriores. ¿Algún día se implementará ese formato de 128 bits en JavaScript?
El redondeo en el cálculo de facturas
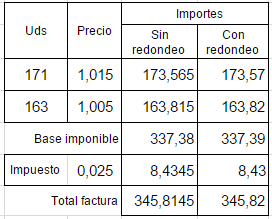
El objetivo final de este tema es resolver problemas reales con importes monetarios donde sólo necesitamos redondear a dos dígitos. En la Figura aparece una captura de pantalla de una hoja de cálculo simulando los cálculos de una factura. He usado la hoja de cálculo de Google Drive.
El redondeo usado es el denominado estándar que hemos definido en el primer apartado de este tema. Tal como indica la ayuda Google Drive, se trata de que al redondear a una posición determinada se debe tener en cuenta el dígito más significativo siguiente (el que queda a la derecha de la posición). Si este dígito es igual o mayor que 5, el dígito se redondea al alza. De lo contrario, se redondea a la baja.
Ese es el redondeo usado en aplicaciones de gestión contable y comercial, que ya comentamos que redondea siempre arriba la fracción 0.5 y que conseguimos usando la función redondearExp().
...Si este dígito es mayor que 5, ...cuando la versión inglesa pone
...If this digit is greater than or equal to 5, ...que es lo que realmente hace el redondeo estándar.
En el siguiente ejemplo interactivo aplicaremos los métodos de redondeo estudiados para ver si conseguimos el mismo resultado que la hoja de cálculo anterior. Tenemos dos líneas de factura. Las unidades y el precio pueden tener un número indefinido de dígitos fraccionarios. Pero el importe de cada línea ha de ser redondeado al número de decimales que precise la moneda en la que se están haciendo los cálculos.
Eso es así pues el importe es una cantidad monetaria, mientras que las unidades y el precio no lo son. Las unidades podría ser kilos, metros o simplemente unidades. El precio es un factor de la forma €/kg, €/m o €/ud. El importe es moneda pues es el producto de algo como X kg × Y €/kg = Z €. Si trabajamos con Euros el importe de cada línea ha de redondearse a dos dígitos fraccionarios que impone esa moneda. La base imponible será finalmente la suma de importes monetarios ya redondeados.
Si hubiera que aplicar un factor de impuesto, también el resultado de la base imponible por ese factor deberá ser redondeado a dos dígitos fraccionarios. El total de factura será la suma de la base imponible más el impuesto, resultado que ya vendrá con dos dígitos fraccionarios pues así ya vienen los sumandos.
En el ejemplo tenemos seis columnas para aplicar a importes sin redondear en la columna (A) y el resto usando todos los métodos que hemos visto en este tema y también toLocaleString(). Para los valores iniciales sólo las columnas (E) y (F) consiguen un resultado correcto. La (E) usa redondearExp(n, 2, true) mientras que la (F) usa el método toLocaleString() con formato de moneda Euro.
Ejemplo: Redondeando facturas
| Uds | Precio | Importes | |||||
|---|---|---|---|---|---|---|---|
| (A) | (B) | (C) | (D) | (E) | (F) | ||
| Base Imponible | |||||||
| Impuesto | |||||||
| Total Factura | |||||||
Las seis columnas se redondean aplicando los siguientes métodos, indicando que tipo devuelve cada uno:
- Sin redondear ⇒ number
n.toFixed(2)⇒ stringredondear(n, 2)⇒ numberredondearExp(n, 2)⇒ numberredondearExp(n, 2, true)⇒ numbern.toLocaleString("es", {style: "currency", currency: "EUR"})⇒ string
Aunque toLocaleString() aplica también el redondeo estándar, el problema es que devuelve un string (como también toFixed()). En cada cálculo parcial habría que realizar una conversión a número. Si el string viene con formato español, las comas de decimales y los puntos de separación de miles son un problema para aplicar una conversión directa con Number() o incluso con parseFloat(). Usamos en el ejemplo una función para realizar esa conversión:
function convertirNumero(str){
//El número vendrá como 1.234.567,89 €
return Number(str.replace(/\./g, "").
replace(/,/, ".").
replace(/[^\d.+-]/g, ""));
}
Pero no deja de ser un engorro, pues hay que hacerlo en cada cálculo parcial. Las funciones redondear() o redondearExp() tienen la ventaja de devolvernos un number.