Desarreglos parciales 2
Desarreglos parciales: Implementando recurrencia
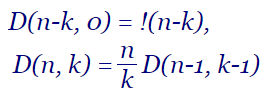
Los desarreglos parciales de una lista con n elementos distintos son todas las sublistas ordenadas con n elementos distintos que se pueden generar de tal forma que solo k elementos aparecen en su posición original. También se pueden definir como las permutaciones de n elementos con k puntos fijos. Las denotamos como D(n, k), correspondiendo con k=0 a los desarreglos sin puntos fijos que vimos en un tema anterior.
En el tema anterior vimos que la recurrencia D(n, k) = n/k D(n-1, k-1), como se observa en la Figura, también nos sirve para calcular el valor numérico de los desarreglos parciales.
| D(n, k) = { | !(n-k) | si k=0 |
| n/k D(n-1, k-1) | si k>0 |
En un tema anterior implementábamos derangeP1(list, k) usando D(n, k) = C(n, k) × D(n-k, 0) para un algoritmo no recursivo que generara desarreglos parciales, haciendo uso de los algoritmos recursivos para generar combinaciones con combine2(list, k) y para generar desarreglos con derange1(list), que a su vez usaba permute3(list) para generar permutaciones. Este tema trata de aprovechar la recurrencia dada D(n, k) = n/k D(n-1, k-1) para implementar otro algoritmo para generar los desarreglos parciales directamente, sin hacer uso del algoritmo que generaba las combinaciones.
Para lograr ese objetivo hemos de evitar el cociente n/k:
| D(n, k) = | n | D(n-1, k-1) = | n (k-1)! | D(n-1, k-1) ⇒ |
| k | k! |
Entonces la definición de la recurrencia queda así
| k! D(n, k) = { | !(n-k) | si k=0 |
| n (k-1)! D(n-1, k-1) | si k>0 |
Si designamos DK(n, k) = k! D(n, k) tenemos esta otra recurrencia
| DK(n, k) = { | !(n-k) | si k=0 |
| n DK(n-1, k-1) | si k>0 |
Como ambas variables bajan de valor la misma cantidad, podemos reducir a una variable:
| DK(n) = { | !b | si n=b |
| n DK(n-1) | si n>b |
Puesta de forma compacta e incrementando índices:
Dividiendo por n+1
| DK(n+1) | = DK(n) |
| n+1 |
Usaremos esta función generadora:
| G(x) = ∑n≥b DK(n) | xn |
| n! |
con estas condiciones iniciales:
| Gb(x) = ∑n=b..b DK(n) | xn | = | !b xb |
| n! | b! |
Aplicando la función generadora a la recurrencia:
| ∑n≥b | DK(n+1) | xn | = ∑n≥b DK(n) | xn |
| n+1 | n! | n! |
El término de la derecha es G(x), con lo que sólo tenemos que desarrollar el término de la izquierda
| ∑n≥b | DK(n+1) | xn | = ∑n≥b DK(n+1) | xn | = |
| n+1 | n! | (n+1)! |
| = ∑n≥b DK(n+1) | xn+1 x-1 | = | 1 | ∑n≥b DK(n+1) | xn+1 | = |
| (n+1)! | x | (n+1)! |
| = | 1 | ∑n≥b+1 DK(n) | xn | = |
| x | n! |
| = | 1 | ( - ∑n=b..b DK(n) | xn | + ∑n≥b DK(n) | xn | ) = |
| x | n! | n! |
| = | 1 | ( - Gb(x) + G(x) ) = | 1 | ( - | !b xb | + G(x) ) |
| x | x | b! |
Entonces llegamos a esta expresión:
| 1 | ( - | !b xb | + G(x) ) = G(x) |
| x | b! |
que simplificamos así:
| - | !b xb | + G(x) = x G(x) |
| b! |
Quedando finalmente esta función generadora:
| G(x) = | !b xb |
| b! (1-x) |
de la cual podemos obtener su serie asociada haciendo esto:
| G(x) = | !b xb | × | 1 | = | !b xb | ∑n≥0 xn | = | !b | ∑n≥0 xn+b | = |
| b! | 1-x | b! | b! |
| = | !b | ∑n≥b xn | = | !b | ∑n≥b n! | xn | = ∑n≥b n! | !b | xn |
| b! | b! | n! | b! | n! |
con lo que finalmente tenemos
| G(x) = | !b xb | = ∑n≥b n! | !b | xn |
| b!(1-x) | b! | n! |
| DK(n) = n! | !b |
| b! |
Resolviendo la recurrencia WolframAlpha que usa el símbolo de Pochchammer, donde veíamos que 1n = n! llegamos al mismo resultado
| DK(n) = n! | !b |
| b! |
Deshaciendo el cambio b = n - k
| DK(n) = n! | !b | = n! | !(n-k) | = k! !(n-k) | n! | = k! !(n-k) C(n, k) = k! D(n, k) |
| b! | (n-k)! | k! (n-k)! |
Por lo tanto
| D(n, k) = | DK(n, k) |
| k! |
Algoritmo derangeP2(list, k) para generar desarreglos parciales
Usando [4] vamos a implementar un algoritmo para generar los desarreglos parciales. Cuando obtengamos los desarreglos de DK(n, k) solo nos quedará quitarle los desarreglos correspondientes a multiplicar por k!, lo que haremos con la función removeDuplicates() con el siguiente algoritmo.
function removeDuplicates(list=[]){
iter += 1;
let obj = {};
for (let arr of list){
iter += 1;
obj[arr] = arr;
}
let res = Object.values(obj);
iter += res.length;
return res;
}
/* D(n, k) = DK(n, k) ÷ k! */
function derangeP2(list=[], k=0) {
let result = [];
if (list.length<k) {
iter += 1;
} else {
/* DK(n, k) = n DK(n-1, k-1) */
function dk(list=[], k=0) {
let res = [];
let n = list.length;
if (k===0) {
/* iter += Td */
res = derange1(list);
} else {
iter += 1;
for (let j=0; j<n; j++){
iter += 1;
let pivot = list[j];
iter += (n-1);
let listMinor = [ ...list.slice(0, j),
...list.slice(j+1)];
let subResult = dk(listMinor, k-1);
/* subResult.length= DK(n-1, k-1) = (k-1)! ×
D(n-1, k-1) =(k-1)! !(n-k) × C(n-1, k-1) */
for (let i=0; i<subResult.length; i++) {
/* subResult[i].length = n-1 */
iter += 1 + subResult[i].length;
res.push([...subResult[i].slice(0, j), pivot,
...subResult[i].slice(j)]);
}
}
}
return res;
}
result = removeDuplicates(dk(list, k));
}
return result;
}El coste del algoritmo externo que recibe la llamada inicial derangeP2(list, k) lo denominaremos T(n, k). Este coste equivale a la implementación de la recurrencia que vimos D(n, k) = n/k D(n-1, k-1). Mientras que el coste del algoritmo interno recursivo dk(list, k) lo denominaremos Tdk(n, k) equiparándose con la otra recurrencia obtenida DK(n, k) = n DK(n-1, k-1).
Una vez obtengamos el coste del algoritmo interno recursivo, el coste del algoritmo externo será el siguiente, donde Trd es el coste de remover los duplicados
Veamos Tdk(n, k) a partir del algoritmo
Simplificando
| = n Tdk(n-1, k-1) + n2 + 1 + !(n-k) n | n! |
| (n-k)! |
Como n-k permanece constante pues las dos variables n y k descienden al mismo tiempo, hacemos lo mismo que vimos en el tema anterior haciendo el cambio b = n-k con lo que nos queda una recurrencia con una única variable n:
| Tdk(n) = n Tdk(n-1) + n2 + 1 + | !b | n! n |
| b! |
Que puesto en forma de definición de recurrencia queda así:
| Tdk(n) = { | Td(b) | si n=b |
| n Tdk(n-1) + n2 + 1 + !b/b! n! n | si n>b |
El caso base es n = b ⇒ n = n-k ⇒ k = 0, como era de esperar pues cuando k=0 entonces n=b. En el caso base se obtienen los desarreglos sin puntos fijos Td(b) usando el algoritmo derange1(list) cuyo coste obtuvimos en ese tema y que aplicado a n = b es:
Siendo Tp a su vez el coste del algoritmo permute3(list) que aplicado a n = b
| Tp(b) = 2b! - 1 + 2 ∑j=2..b | b! |
| j! |
Resolvamos la siguiente recurrencia aplicando la técnica de la función generadora
| Tdk(n) = n Tdk(n-1) + n2 + 1 + | !b | n! n |
| b! |
Incrementamos índices
| Tdk(n+1) = (n+1) Tdk(n) + (n+1)2 + 1 + | !b | (n+1)! (n+1) |
| b! |
Dividimos por n+1
| Tdk(n+1) | = Tdk(n) + (n+1) + | 1 | + | !b | (n+1)! |
| n+1 | n+1 | b! |
Usando esta función generadora
| G(x) = ∑n≥b Tdk(n) | xn |
| n! |
Con estas condiciones iniciales
| Gb(x) = ∑n=b..b Tdk(n) | xn | = Tdk(b) | xb | = Td(b) | xb |
| n! | b! | b! |
Aplicamos sumatorios
| ∑n≥b | Tdk(n+1) | xn | = ∑n≥b Tdk(n) | xn | + ∑n≥b (n+1) | xn | + |
| n+1 | n! | n! | n! |
| + ∑n≥b | 1 | xn | + ∑n≥b | !b | (n+1)! | xn |
| n+1 | n! | b! | n! |
Resolvemos partiendo de la izquierda:
∑n≥b Tdk(n+1) xn = ∑n≥b Tdk(n+1) xn = n+1 n! (n+1)! = ∑n≥b Tdk(n+1) xn+1 x-1 = 1 ∑n≥b Tdk(n+1) xn+1 = (n+1)! x (n+1)! = 1 ∑n≥b+1 Tdk(n) xn = x n! = 1 ( - ∑n=b..b Tdk(n) xn + ∑n≥b Tdk(n) xn ) = x n! n! = 1 ( - Gb(x) + G(x) ) = x = 1 ( - Td(b) xb + G(x) ) x b! ∑n≥b Tdk(n) xn = G(x) n! ∑n≥b (n+1) xn = ∑n≥b n xn + ∑n≥b xn = n! n! n! = xb - (1+x) ∑n=0..b-1 xn + (1+x) ex (b-1)! n! Se resuelve en estas dos partes:
∑n≥b xn = - ∑n=0..b-1 xn + ∑n≥0 xn = - ∑n=0..b-1 xn + ex n! n! n! n! Hemos aplicado la conocida serie exponencial ∑n≥0 xn/n! = ex
∑n≥b n xn = - ∑n=0..b-1 n xn + ∑n≥0 n xn = - ∑n=0..b-1 n xn + x ex = n! n! n! n! = - ∑n=0..b-1 xn + x ex = - ∑n=0..b-1 xn-1 x + x ex = (n-1)! (n-1)! = - x ∑n=0..b-1 xn-1 + x ex = - x ∑n=-1..b-2 xn + x ex = (n-1)! n! = - x ( ∑n=-1..-1 xn - ∑n=b-1..b-1 xn + ∑n=0..b-1 xn ) + x ex = n! n! n! = - x ( x-1 - xb-1 + ∑n=0..b-1 xn ) + x ex = (-1)! (b-1)! n! = xb - x ∑n=0..b-1 xn + x ex = (b-1)! n! En la primera línea hemos resuelto ∑n≥0 n xn/n! = x ex aplicando derivadas de una serie donde se expone exactamente este caso.
En la quinta línea hemos resuelto x-1/(-1)! = 0 por lo que vimos en un tema sobre la función Gamma y 1/(-n)!
∑n≥b 1 xn = ∑n≥b xn = ∑n≥b xn+1 x-1 = 1 ∑n≥b xn+1 = n+1 n! (n+1)! (n+1)! x (n+1)! = 1 ( - ∑n=0..b-1 xn+1 + ∑n≥0 xn+1 ) = x (n+1)! (n+1)! = 1 ( - ∑n=0..b-1 xn+1 + ex - 1 ) = x (n+1)! = 1 ( - ∑n=1..b xn + ex - 1 ) = x n! = 1 ( - ( - ∑n=0..0 xn + ∑n=b..b xn + ∑n=0..b-1 xn ) + ex - 1 ) = x n! n! n! = 1 ( - ( - 1 + xb + ∑n=0..b-1 xn ) + ex - 1 ) = x b! n! = 1 - xb-1 - 1 ∑n=0..b-1 xn + ex - 1 x b! x n! x x =- xb-1 - 1 ∑n=0..b-1 xn + ex b! x n! x En la tercera línea hemos resuelto esto
∑n≥0 xn+1/(n+1)! = ∑n≥1 xn/n! = - x0/0! + ∑n≥0 xn/n! = -1+ex∑n≥b !b (n+1)! xn = !b ∑n≥b (n+1)! xn = !b ∑n≥b (n+1) xn = b! n! b! n! b! = !b ( - ∑n=0..b-1 (n+1) xn + ∑n≥0 (n+1) xn ) = b! = !b ( - b xb+1 - (b+1) xb + 1 + 1 ) = b! (1-x)2 (1-x)2 = - !b b xb+1 + !b (b+1) xb b! (1-x)2 b! (1-x)2 En la tercera línea hemos resuelto ∑n=0..b-1 (n+1) xn de forma similar a como lo hicimos en un tema anterior y se puede comprobar en WolframAlpha.
Por otro lado la otra serie se puede resolver así
∑n≥0 (n+1) xn = ∑n≥0 (n+1) xn+1 x-1== 1 ∑n≥0 (n+1) xn+1 = 1 ∑n≥1 n xn = 1 x = 1 x x x (1-x)2 (1-x)2 aplicando derivadas de una serie a ∑n≥1 n xn con el principio visto en ese tema que decía x A'(x) = ∑n≥1 n an xn siendo an = 1 en la serie A(x) = ∑n≥0 xn = 1/(1-x) con su derivada A'(x) = 1/(1-x)2 con lo que resolvemos x A'(x) = x/(1-x)2.
Agrupando los resultados de A) hasta E) en [6]
| 1 | ( - Td(b) | xb | + G(x) ) = G(x) + |
| x | b! |
| + | xb | - (1+x) ∑n=0..b-1 | xn | + (1+x) ex - |
| (b-1)! | n! |
| - | xb-1 | - | 1 | ∑n=0..b-1 | xn | + | ex | - |
| b! | x | n! | x |
| - | !b | b | xb+1 | + | !b | (b+1) | xb |
| b! | (1-x)2 | b! | (1-x)2 |
Pasando x a la derecha
| - Td(b) | xb | + G(x) = x G(x) + |
| b! |
| + | xb+1 | - x(1+x) ∑n=0..b-1 | xn | + x(1+x) ex - |
| (b-1)! | n! |
| - | xb | - | ∑n=0..b-1 | xn | + ex - |
| b! | n! |
| - | !b | b | xb+2 | + | !b | (b+1) | xb+1 |
| b! | (1-x)2 | b! | (1-x)2 |
Reagrupando para dejar G(x) a la izquierda
| = (x2+x+1) ( - ∑n=0..b-1 | xn | + ex ) + |
| n! |
| + | Td(b) xb | + | xb+1 | - | xb | - |
| b! | (b-1)! | b! |
| - | !b | b | xb+2 | + |
| b! | (1-x)2 |
| + | !b | (b+1) | xb+1 |
| b! | (1-x)2 |
Pasando 1-x obtenemos la función generadora final:
| = | x2+x+1 | ( - ∑n=0..b-1 | xn | + ex ) + |
| 1-x | n! |
| + | (Td(b) - 1) xb | + | xb+1 | - |
| b! (1-x) | (b-1)! (1-x) |
| - | !b | b | xb+2 | + |
| b! | (1-x)3 |
| + | !b | (b+1) | xb+1 |
| b! | (1-x)3 |
Busquemos series para cada línea anterior:
x2+x+1 ( - ∑n=0..b-1 xn + ex ) = 1-x n! = x2+x+1 ( - ∑n=0..b-1 xn + ∑n≥0 xn ) = 1-x n! n! = x2+x+1 ∑n≥b xn 1-x n! Para resolver esto hacemos lo mismo que vimos en un tema anterior, resolviendo el sumatorio final para el rango n≥0 y luego ajustando índices, haciendo uso de lo visto en el tema de las K-Tuplas para resolver funciones como xk ex/(1-x)
x2+x+1 ∑n≥0 xn = x2+x+1 ex = 1-x n! 1-x = x2 ex + x ex + ex = 1-x 1-x 1-x = ∑n≥0 ( ∑j=0..n-2 n! + ∑j=0..n-1 n! + ∑j=0..n n! ) xn = j! j! j! n! = ∑n≥0 ( (- n! - n! + ∑j=0..n n! ) + (- n! + ∑j=0..n n! ) + ∑j=0..n n! ) xn = (n-1)! n! j! n! j! j! n! = ∑n≥0 ( - (n+2) + 3 ∑j=0..n n! ) xn j! n! Y ahora ajustamos índices tal como hicimos en el tema que comentamos antes:
x2+x+1 ∑n≥b xn = x2+x+1 ex = 1-x n! 1-x = ∑n≥b ( - (n+2) + 3 ∑j=b..n n! ) xn j! n! (Td(b) - 1) xb + xb+1 = Td(b) - 1 + b ∑n≥b n! xn b! (1-x) (b-1)! (1-x) b! n! Hemos alcanzado ese resultado en estas dos partes:
(Td(b) - 1) xb = Td(b) - 1 xb 1 = Td(b) - 1 xb ∑n≥0 xn = b! (1-x) b! 1-x b! = Td(b) - 1 ∑n≥0 xn+b = Td(b) - 1 ∑n≥b n! xn b! b! n! xb+1 = b xb+1 = b xb x = b xb ∑n≥1 xn = (b-1)! (1-x) b! 1-x b! 1-x b! = b ∑n≥1 xn+b = b ∑n≥b+1 xn = - ∑n=b..b xn + ∑n≥b+1 xn = b! b! = -xb + b ∑n≥b xn = b ∑n≥b n! xn b! b! n! En la última línea hemos ignorado el término xb. Y es algo que ya vimos en ese tema anterior que ya hemos comentado. Además de lo visto en ese tema, ahora también podemos añadir otra perspectiva observando la definición de la función que interviene cuando ajustamos el rango en el sumatorio ∑n≥b+1 xn, como se observa en WolframAlpha, tomando como ejemplo b=5 en la función xb+1/(1-x)
x5+1 = 1-x ∑n≥0(({ 1 if n>5 ) xn) = 0 otherwise = ∑n≥5+1 xnSe observa que para b≤5 la función tiene el término cero, es decir, aunque la escribamos como ∑n≥b+1 xn hemos de entender que para n<b+1 los términos de la serie resultan cero, por lo que ∑n=b..b xn = 0 xb = 0.
- !b b xb+2 = !b b xb+2 1 = b! (1-x)3 b! (1-x)3 = - !b b xb+2 ∑n≥0 ½ (n+2)(n+1) xn = b! = - !b b ∑n≥0 ½ (n+2)(n+1) xn+b+2 = b! = - !b b ∑n≥b ½ (n-b+2)(n-b+1) xn+2 = b! = - !b b ∑n≥b+2 ½ (n-b)(n-b-1) xn = b! = - !b b ( - ∑n=b..b ½ (n-b)(n-b-1) xn - ∑n=b+1..b+1 ½ (n-b)(n-b-1) xn + ∑n≥b ½ (n-b)(n-b-1) xn ) = b! = - !b b ( - 0 - 0 + ∑n≥b ½ (n-b)(n-b-1) xn ) = b! = - !b b ∑n≥b ½ (n-b)(n-b-1) n! xn b! n! En la primera línea aplicamos lo que resolvimos en un tema tema anterior con el desarrollo de Taylor:
1 = ∑n≥0 (n+2)! xn = ∑n≥0 ½ (n+2)(n+1) xn (1-x)3 2 n! - !b (b+1) xb+1 = !b (b+1) xb+1 1 = b! (1-x)3 b! (1-x)3 = - !b (b+1) xb+1 ∑n≥0 ½ (n+2)(n+1) xn = b! = - !b (b+1) ∑n≥0 ½ (n+2)(n+1) xn+b+1 = b! = - !b (b+1) ∑n≥b ½ (n-b+2)(n-b+1) xn+1 = b! = - !b (b+1) ∑n≥b+1 ½ (n-b+1)(n-b) xn = b! = - !b (b+1) ( - ∑n=b..b ½ (n-b)(n-b+1) xn + ∑n≥b ½ (n-b)(n-b+1) xn ) = b! = - !b (b+1) ( - 0 + ∑n≥b ½ (n-b)(n-b+1) xn ) = b! = - !b (b+1) ∑n≥b ½ (n-b)(n-b+1) n! xn b! n!
Agrupando los resultados obtenidos en los apartados i), ii), iii) y iv) anterior obtenemos la solución del algoritmo recursivo dk(list, k) con b=n-k
| Tdk(n) = 3 ∑j=b..n | n! | - (n+2) + | Td(b) - 1 + b | n! - | !b | b ½ (n-b)(n-b-1) n! | + | !b | (b+1) ½ (n-b)(n-b+1) n! |
| j! | b! | b! | b! |
Reagrupando los términos de la derecha:
| Tdk(n) = 3 ∑j=b..n | n! | - (n+2) + | n! | ( Td(b) + b - 1 + ½ !b (n-b)(n+b+1) ) |
| j! | b! |
Deshaciendo el cambio b=n-k
| Tdk(n, k) = 3 ∑j=n-k..n | n! | - (n+2) + | n! | (Td(n-k)+n-k-1+!(n-k) | k(2n-k+1) | ) |
| j! | (n-k)! | 2 |
Eliminando duplicados para obtener los desarreglos parciales
El siguiente paso es eliminar los duplicados
Recordemos que
| DK(n, b) = n! | !b |
| b! |
Mientras que deshaciendo el cambio b=n-k llegamos a
| DK(n, k) = n! | !(n-k) | = k! !(n-k) | n! | = k! !(n-k) C(n, k) = k! D(n, k) |
| (n-k)! | k! (n-k)! |
Así que con el algoritmo recursivo dk(list, k) cuya longitud de la lista es de n elementos obtenemos DK(n, k) = k! !(n-k) C(n, k) resultados. Analizamos entonces en el algoritmo que elimina duplicados una lista con esos elementos, para obtener finalmente D(n, k) = !(n-k) C(n, k) resultados.
function removeDuplicates(list=[]){
iter += 1;
let obj = {};
/* list.length = k! !(n-k) C(n, k) */
for (let arr of list){
iter += 1;
obj[arr] = arr;
}
/* res.length = !(n-k) C(n, k) */
let res = Object.values(obj);
iter += res.length;
return res;
}de donde
Entonces como T(n, k) = Tdk(n, k) + Trd(n, k) la solución final queda así, haciendo un ajuste para el caso n<k tenemos la fórmula que calcula las iteraciones del algoritmo derangeP2(list, k) que genera los desarreglos parciales basado en la recurrencia D(n, k) = n/k D(n-1, k-1)
| + 3 ∑j=n-k..n | n! | - (n+2) + | n! | (Td(n-k)+n-k-1+!(n-k) | k(2n-k+1) | ) |
| j! | (n-k)! | 2 |
Recordando que Td era el coste del algoritmo derange1(list) con b=n-k
Y Tp a su vez el coste del algoritmo permute3(list)
| Tp(b) = 2b! - 1 + 2 ∑j=2..b | b! |
| j! |
En caso de coste con copia sólo hay que actuar sobre el coste de las permutaciones:
| Tp(b) = b b! + 2b! - 1 + 2 ∑j=2..b | b! |
| j! |
En la herramienta Combine Tools podemos obtener una tabla que ejecuta el algoritmo derangeP2(list, k) para un rango de valores, anotando en cada celda el contaje de iteraciones y el valor calculado con la fórmula anterior, observándose que coincide en todos los casos.
| n↓k→ | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 6 6 | 1 1 | 1 1 | 1 1 | 1 1 |
| 1 | 5 5 | 9 9 | 1 1 | 1 1 | 1 1 |
| 2 | 14 14 | 14 14 | 25 25 | 1 1 | 1 1 |
| 3 | 44 44 | 59 59 | 50 50 | 99 99 | 1 1 |
| 4 | 192 192 | 222 222 | 292 292 | 214 214 | 503 503 |
| 5 | 1032 1032 | 1207 1207 | 1312 1312 | 1762 1762 | 1092 1092 |